{
"cells": [
{
"cell_type": "markdown",
"metadata": {
"id": "view-in-github",
"colab_type": "text"
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "4QIfKc-Me5Ni"
},
"source": [
"# Behler-Parrinello Fitting Neural Network with Machine Learning Potential (BP-FNN MLP) Models for the Claisen Rearrangement\n",
"\n",
"For this tutorial, we will be combining the Fitting Neural Network (FNN) from Lesson 1 and the Behler-Parrinello Neural Network (BPNN) from Lesson 3 to train a $\\Delta$ Machine Learning Potential ($\\Delta$MLP) model to reproduce the energy and forces for the claisen rearrangement reaction. With a BP-FNN, we can utilize the symmetry functions from the BPNN model for feature extraction and use the FNN for training. The goal of this model is to train with data that is from the semiempirical (PM3) and DFT (B3LYP) levels of theory. The BP-FNN will be used to correct the semiempirical values to obtain DFT level accuracy, that makes it a $\\Delta$MLP model.\n",
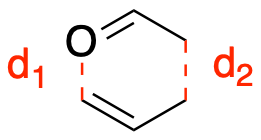
"The reaction coordinate is constructed by stretching the $d_2$ bond distance, while shrinking the $d_1$ bond distance. The reaction is sampled with 21 windows along the $d_1-d_2$ reaction coordinate.\n",
"\n",
"Total of 2100 frames (1 ps/window) are saved every 1 fs.\n",
"\n",
"
"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "4QIfKc-Me5Ni"
},
"source": [
"# Behler-Parrinello Fitting Neural Network with Machine Learning Potential (BP-FNN MLP) Models for the Claisen Rearrangement\n",
"\n",
"For this tutorial, we will be combining the Fitting Neural Network (FNN) from Lesson 1 and the Behler-Parrinello Neural Network (BPNN) from Lesson 3 to train a $\\Delta$ Machine Learning Potential ($\\Delta$MLP) model to reproduce the energy and forces for the claisen rearrangement reaction. With a BP-FNN, we can utilize the symmetry functions from the BPNN model for feature extraction and use the FNN for training. The goal of this model is to train with data that is from the semiempirical (PM3) and DFT (B3LYP) levels of theory. The BP-FNN will be used to correct the semiempirical values to obtain DFT level accuracy, that makes it a $\\Delta$MLP model.\n",
"The reaction coordinate is constructed by stretching the $d_2$ bond distance, while shrinking the $d_1$ bond distance. The reaction is sampled with 21 windows along the $d_1-d_2$ reaction coordinate.\n",
"\n",
"Total of 2100 frames (1 ps/window) are saved every 1 fs.\n",
"\n",
" "
]
},
{
"cell_type": "code",
"source": [
"from IPython.display import HTML\n",
"\n",
"HTML(f\"\"\"\"\"\")"
],
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 321
},
"id": "ljBOLgk-wLWI",
"outputId": "c8595e33-a151-42a8-dc40-29973771c800"
},
"execution_count": 1,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
""
],
"text/html": [
""
]
},
"metadata": {},
"execution_count": 1
}
]
},
{
"cell_type": "markdown",
"source": [
"## Importing PyTorch Lightning and Libraries\n",
"We will first install PyTorch Lightning and import libraries needed to train our machine learning models."
],
"metadata": {
"id": "BPuN7hFOFT5L"
}
},
{
"cell_type": "code",
"source": [
"%%capture\n",
"!pip install pytorch-lightning > /dev/null\n",
"import math\n",
"import numpy as np\n",
"from typing import Sequence, Tuple\n",
"\n",
"import torch\n",
"import torch.nn as nn\n",
"import torch.nn.functional as F\n",
"from torch import Tensor\n",
"\n",
"from torch.utils.data import TensorDataset, DataLoader, random_split\n",
"import pytorch_lightning as pl\n",
"from pytorch_lightning import loggers as pl_loggers"
],
"metadata": {
"id": "fPn6Q6URnYDN"
},
"execution_count": 2,
"outputs": []
},
{
"cell_type": "markdown",
"source": [
"## Defining Symmetry Functions\n",
"\n",
"We will define the BP and ANI symmetry functions to ensure that our ML predictions are invariant to translations, rotations, and permutations.\n",
"\n",
"- **pairwise_vector:** Distance function for calculating distances between each atom.\n",
"\n",
"- **symmetry_function_g1:** BP radial symmetry function.\n",
"\n",
"- **symmetry_function_g2:** BP angular symmetry function.\n",
"\n",
"- **symmetry_function_g2ani:** ANI angular symmetry function.\n"
],
"metadata": {
"id": "VbFZM9qAsPwK"
}
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"id": "tzRTvSuqsPwM"
},
"outputs": [],
"source": [
"def pairwise_vector(coords: Tensor) -> Tensor:\n",
" num_batches, num_channels, _ = coords.size()\n",
" rij = coords[:, :, None] - coords[:, None]\n",
" mask = ~torch.eye(num_channels, dtype=torch.bool, device=coords.device) # remove self-interaction\n",
" rij = torch.masked_select(rij, mask.unsqueeze(2)).view(num_batches, num_channels, num_channels - 1, 3)\n",
" return rij\n",
"\n",
"\n",
"def symmetry_function_g1(rij: Tensor, Rcr: float, EtaR: Tensor, ShfR: Tensor) -> Tensor:\n",
" dij = torch.norm(rij, dim=3)\n",
" fij = (torch.cos(dij / Rcr * math.pi) + 1) * 0.5 * (dij <= Rcr)\n",
" g1 = torch.sum(torch.exp(-EtaR.unsqueeze(dim=1) * (dij.unsqueeze(dim=-1) - ShfR.unsqueeze(dim=1))**2) * fij.unsqueeze(dim=-1), dim=2)\n",
" return g1\n",
"\n",
"\n",
"def symmetry_function_g2(rij: Tensor, Rca: float, Zeta: Tensor, EtaA: Tensor, LamA: Tensor) -> Tensor:\n",
" c = torch.combinations(torch.arange(rij.size(2)), r=2)\n",
" rij = rij[:, :, c]\n",
" r12 = rij[:, :, :, 0]\n",
" r13 = rij[:, :, :, 1]\n",
" r23 = r12 - r13\n",
" d12 = torch.norm(r12, dim=3)\n",
" d13 = torch.norm(r13, dim=3)\n",
" d23 = torch.norm(r23, dim=3)\n",
" f12 = (torch.cos(d12 / Rca * math.pi) + 1) * 0.5\n",
" f13 = (torch.cos(d13 / Rca * math.pi) + 1) * 0.5\n",
" f23 = (torch.cos(d23 / Rca * math.pi) + 1) * 0.5\n",
" cosine = torch.einsum('ijkl,ijkl->ijk', r12, r13) / (d12 * d13)\n",
"\n",
" g2 = torch.sum(2**(1 - Zeta.unsqueeze(dim=1)) * (1 + LamA.unsqueeze(dim=1) * cosine.unsqueeze(dim=-1))**Zeta.unsqueeze(dim=1) * torch.exp(-EtaA.unsqueeze(dim=1) * (d12**2 + d13**2 + d23**2).unsqueeze(dim=-1)) * (f12 * f13 * f23).unsqueeze(dim=-1), dim=2)\n",
" return g2\n",
"\n",
"\n",
"def symmetry_function_g2ani(rij: Tensor, Rca: float, Zeta: Tensor, ShfZ: Tensor, EtaA: Tensor, ShfA: Tensor) -> Tensor:\n",
" c = torch.combinations(torch.arange(rij.size(2)), r=2)\n",
" rij = rij[:, :, c]\n",
" r12 = rij[:, :, :, 0]\n",
" r13 = rij[:, :, :, 1]\n",
" r23 = r12 - r13\n",
" d12 = torch.norm(r12, dim=3)\n",
" d13 = torch.norm(r13, dim=3)\n",
" f12 = (torch.cos(d12 / Rca * math.pi) + 1) * 0.5\n",
" f13 = (torch.cos(d13 / Rca * math.pi) + 1) * 0.5\n",
" cosine = torch.einsum('ijkl,ijkl->ijk', r12, r13) / (d12 * d13)\n",
" cosine = torch.cos(torch.acos(cosine).unsqueeze(dim=-1) - ShfA.unsqueeze(dim=1))\n",
"\n",
" g2 = torch.sum(2**(1 - Zeta.unsqueeze(dim=1)) * (1 + cosine)**Zeta.unsqueeze(dim=1) * torch.exp(-EtaA.unsqueeze(dim=1) * (0.5 * (d12 + d13).unsqueeze(dim=-1) - ShfZ.unsqueeze(dim=1))**2) * (f12 * f13).unsqueeze(dim=-1), dim=2)\n",
" return g2"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "826_ckjtgmp2"
},
"source": [
"## Defining Neural Network and Feature Extraction Classes\n",
"\n",
"We will now define feature extraction classes which will be used in our Behler-Parrinello and ANI neural networks.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "oCSkqkOrgmp2"
},
"source": [
"### Defining Sequential and Dense Classes\n",
"\n",
"The Sequential class contains the function for the feed-forward aspect of our neural network.\n",
"The Dense class contains functions to describe a densely connected neural network."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"id": "WXspRElYvr5n"
},
"outputs": [],
"source": [
"class Sequential(nn.Sequential):\n",
" def forward(self, input: Tuple[Tensor, Tensor]) -> Tuple[Tensor, Tensor]:\n",
" for module in self:\n",
" input = module(input)\n",
" return input\n",
"\n",
"class Dense(nn.Module):\n",
" def __init__(self, num_channels: int, in_features: int, out_features: int, bias: bool = True, activation: bool = False, residual: bool = False) -> None:\n",
" super().__init__()\n",
" self.num_channels = num_channels\n",
" self.in_features = in_features\n",
" self.out_features = out_features\n",
" self.weight = nn.Parameter(torch.Tensor(num_channels, out_features, in_features))\n",
" if bias:\n",
" self.bias = nn.Parameter(torch.Tensor(num_channels, out_features))\n",
" else:\n",
" self.register_parameter('bias', None)\n",
" self.activation = activation\n",
" self.residual = residual\n",
" self.reset_parameters()\n",
"\n",
" def reset_parameters(self) -> None:\n",
" for w in self.weight:\n",
" nn.init.kaiming_uniform_(w, a=math.sqrt(5))\n",
" if self.bias is not None:\n",
" for b, w in zip(self.bias, self.weight):\n",
" fan_in, _ = nn.init._calculate_fan_in_and_fan_out(w)\n",
" bound = 1 / math.sqrt(fan_in)\n",
" nn.init.uniform_(b, -bound, bound)\n",
"\n",
" def forward(self, input: Tuple[Tensor, Tensor]) -> Tuple[Tensor, Tensor]:\n",
" x, channels = input\n",
" weight: Tensor = self.weight[channels]\n",
" output: Tensor = torch.bmm(x.transpose(0, 1), weight.transpose(1, 2)).transpose(0, 1)\n",
"\n",
" if self.bias is not None:\n",
" bias = self.bias[channels]\n",
" output = output + bias\n",
"\n",
" if self.activation:\n",
" output = torch.tanh(output)\n",
"\n",
" if self.residual:\n",
" if output.shape[2] == x.shape[2]:\n",
" output = output + x\n",
" elif output.shape[2] == x.shape[2] * 2:\n",
" output = output + torch.cat([x, x], dim=2)\n",
" else:\n",
" raise NotImplementedError(\"Not implemented\")\n",
"\n",
" return output, channels\n",
"\n",
" def extra_repr(self) -> str:\n",
" return 'num_channels={}, in_features={}, out_features={}, bias={}, activation={}, residual={}'.format(\n",
" self.num_channels, self.in_features, self.out_features, self.bias is not None, self.activation, self.residual\n",
" )"
]
},
{
"cell_type": "markdown",
"source": [
"### Defining the BP Feature Class\n",
"\n",
"Now we will create the feature class, which takes input information and uses functions to extract characteristics unique to the called input features. Here we will be using the previously defined symmetry functions for feature extraction.\n"
],
"metadata": {
"id": "SUdKJjQLK4Wz"
}
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"id": "rRXofpIJkKnd"
},
"outputs": [],
"source": [
"class Feature(nn.Module):\n",
" def __init__(self, Rcr: float, EtaR: Tensor, ShfR: Tensor, Rca: float, Zeta: Tensor, EtaA: Tensor, LamA: Tensor) -> None:\n",
" super().__init__()\n",
" assert len(EtaR) == len(ShfR) == len(LamA)\n",
" assert len(Zeta) == len(EtaA)\n",
" self.Rcr = Rcr\n",
" self.Rca = Rca\n",
" self.EtaR = torch.Tensor(EtaR)\n",
" self.ShfR = torch.Tensor(ShfR)\n",
" self.Zeta = torch.Tensor(Zeta)\n",
" self.EtaA = torch.Tensor(EtaA)\n",
" self.LamA = torch.Tensor(LamA)\n",
"\n",
" def forward(self, coords: Tensor, atom_types: Tensor) -> Tensor:\n",
" num_batches, num_channels, _ = coords.size()\n",
" rij = pairwise_vector(coords)\n",
" EtaR = self.EtaR.to(device=coords.device)[atom_types]\n",
" ShfR = self.ShfR.to(device=coords.device)[atom_types]\n",
" Zeta = self.Zeta.to(device=coords.device)[atom_types]\n",
" EtaA = self.EtaA.to(device=coords.device)[atom_types]\n",
" LamA = self.LamA.to(device=coords.device)[atom_types]\n",
" g1 = symmetry_function_g1(rij, self.Rcr, EtaR, ShfR)\n",
" g2 = symmetry_function_g2(rij, self.Rca, Zeta, EtaA, LamA)\n",
"\n",
" return torch.concat((g1, g2), dim=2)\n",
"\n",
" @property\n",
" def output_length(self) -> int:\n",
" return len(self.EtaR[0]) + len(self.EtaA[0])"
]
},
{
"cell_type": "markdown",
"source": [
"### Defining the ANI Feature Class\n",
"\n",
"We will create a similar feature class for ANI that uses the ANI angle symmetry function.\n"
],
"metadata": {
"id": "id6zvxx-K_yu"
}
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"id": "st4TXB2yeW6v"
},
"outputs": [],
"source": [
"class FeatureANI(nn.Module):\n",
" def __init__(self, Rcr: float, EtaR: Tensor, ShfR: Tensor, Rca: float, Zeta: Tensor, ShfZ: Tensor, EtaA: Tensor, ShfA: Tensor) -> None:\n",
" super().__init__()\n",
" assert len(EtaR) == len(ShfR)\n",
" assert len(Zeta) == len(ShfZ) == len(EtaA) == len(ShfA)\n",
" self.Rcr = Rcr\n",
" self.Rca = Rca\n",
" self.EtaR = torch.Tensor(EtaR)\n",
" self.ShfR = torch.Tensor(ShfR)\n",
" self.Zeta = torch.Tensor(Zeta)\n",
" self.ShfZ = torch.Tensor(ShfZ)\n",
" self.EtaA = torch.Tensor(EtaA)\n",
" self.ShfA = torch.Tensor(ShfA)\n",
"\n",
" def forward(self, coords: Tensor, atom_types: Tensor) -> Tensor:\n",
" num_batches, num_channels, _ = coords.size()\n",
" rij = pairwise_vector(coords)\n",
" EtaR = self.EtaR.to(device=coords.device)[atom_types]\n",
" ShfR = self.ShfR.to(device=coords.device)[atom_types]\n",
" Zeta = self.Zeta.to(device=coords.device)[atom_types]\n",
" ShfZ = self.ShfZ.to(device=coords.device)[atom_types]\n",
" EtaA = self.EtaA.to(device=coords.device)[atom_types]\n",
" ShfA = self.ShfA.to(device=coords.device)[atom_types]\n",
" g1 = symmetry_function_g1(rij, self.Rcr, EtaR, ShfR)\n",
" g2 = symmetry_function_g2ani(rij, self.Rca, Zeta, ShfZ, EtaA, ShfA)\n",
"\n",
" return torch.concat((g1, g2), dim=2)\n",
"\n",
" @property\n",
" def output_length(self) -> int:\n",
" return len(self.EtaR[0]) + len(self.EtaA[0])"
]
},
{
"cell_type": "markdown",
"source": [
"### Creating the Fitting Neural Network\n",
"\n",
"Now we create the Fitting class, which will use the dense neural network for fitting.\n"
],
"metadata": {
"id": "YJsBu7NoLFzC"
}
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"id": "02e3WPabvjIl"
},
"outputs": [],
"source": [
"class Fitting(nn.Module):\n",
" def __init__(self, n_types: int, in_features: int, neuron: Sequence[int] = [240, 240, 240]) -> None:\n",
" super().__init__()\n",
" layers = [Dense(n_types, in_features, neuron[0], activation=True)]\n",
" for i in range(len(neuron)-1):\n",
" layers.append(Dense(n_types, neuron[i], neuron[i+1], activation=True, residual=True))\n",
" layers.append(Dense(n_types, neuron[-1], 1))\n",
" self.fitting_net = Sequential(*layers)\n",
"\n",
" def forward(self, input : Tuple[Tensor, Tensor]) -> Tensor:\n",
" output, _ = self.fitting_net(input)\n",
" return output"
]
},
{
"cell_type": "markdown",
"source": [
"### The Behler-Parrinello Fitting Neural Network (BP-FNN)\n",
"\n",
"We create the BPNN class that can be used for feature extraction with the symmetry functions.\n"
],
"metadata": {
"id": "7YTxfJXgLKsy"
}
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"id": "Gw-8zbn_wPz5"
},
"outputs": [],
"source": [
"class BPNN(pl.LightningModule):\n",
" def __init__(self, descriptor: nn.Module, fitting_net: nn.Module, learning_rate=5e-4) -> None:\n",
" super().__init__()\n",
" self.descriptor = descriptor\n",
" self.fitting_net = fitting_net\n",
" self.learning_rate = learning_rate\n",
"\n",
" def forward(self, coords: torch.Tensor, atom_types: torch.Tensor):\n",
" coords.requires_grad_()\n",
" descriptors = self.descriptor(coords, atom_types)\n",
" atomic_energies = self.fitting_net((descriptors, atom_types))\n",
" energy = torch.unbind(torch.sum(atomic_energies, dim=1))\n",
" gradient, = torch.autograd.grad(energy, [coords], create_graph=True)\n",
" return torch.hstack(energy), gradient\n",
"\n",
" def training_step(self, batch, batch_idx):\n",
" qm_coord, atom_types, energy, gradient = batch\n",
" ene_pred, grad_pred = self(qm_coord, atom_types[0])\n",
" ene_loss = F.mse_loss(ene_pred, energy)\n",
" grad_loss = F.mse_loss(grad_pred, gradient)\n",
"\n",
" lr = self.optimizers().optimizer.param_groups[0]['lr']\n",
" start_lr = self.optimizers().optimizer.param_groups[0]['initial_lr']\n",
" w_ene = 1\n",
" w_grad = 1 + 99 * (lr / start_lr)\n",
"\n",
" loss = w_ene / (w_ene + w_grad) * ene_loss + w_grad / (w_ene + w_grad) * grad_loss\n",
" self.log('train_loss', loss)\n",
" self.log('l2_trn', torch.sqrt(loss))\n",
" self.log('l2_e_trn', torch.sqrt(ene_loss))\n",
" self.log('l2_f_trn', torch.sqrt(grad_loss))\n",
" return loss\n",
"\n",
" def validation_step(self, batch, batch_idx):\n",
" torch.set_grad_enabled(True)\n",
" qm_coord, atom_types, energy, gradient = batch\n",
" ene_pred, grad_pred = self(qm_coord, atom_types[0])\n",
" ene_loss = F.mse_loss(ene_pred, energy)\n",
" grad_loss = F.mse_loss(grad_pred, gradient)\n",
"\n",
" lr = self.optimizers().optimizer.param_groups[0]['lr']\n",
" start_lr = self.optimizers().optimizer.param_groups[0]['initial_lr']\n",
" w_ene = 1\n",
" w_grad = 1 + 99 * (lr / start_lr)\n",
"\n",
" loss = w_ene / (w_ene + w_grad) * ene_loss + w_grad / (w_ene + w_grad) * grad_loss\n",
" self.log('val_loss', loss)\n",
" self.log('l2_tst', torch.sqrt(loss))\n",
" self.log('l2_e_tst', torch.sqrt(ene_loss))\n",
" self.log('l2_f_tst', torch.sqrt(grad_loss))\n",
" self.log('lr', lr)\n",
" return loss\n",
"\n",
" def configure_optimizers(self):\n",
" optimizer = torch.optim.Adam(self.parameters(), lr=self.learning_rate)\n",
" scheduler = {'scheduler': torch.optim.lr_scheduler.ExponentialLR(optimizer, 0.95),\n",
" 'interval': 'epoch',\n",
" 'frequency': 10,\n",
" }\n",
" return [optimizer], [scheduler]"
]
},
{
"cell_type": "markdown",
"source": [
"## Importing Data and Seeding\n",
"\n",
"We will now import our semiempirical and DFT calculation data. We will then use seeding to generate random but reproducible training."
],
"metadata": {
"id": "-7Tv-R5NJSuF"
}
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"id": "vuHEYr6CCf5u"
},
"outputs": [],
"source": [
"ds = np.DataSource(None)\n",
"qm_coord = np.array(np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_coord.npy\", \"rb\")), dtype=\"float32\")\n",
"atom_types = np.loadtxt(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_elem.txt\", \"r\"), dtype=int)\n",
"elems = np.unique(atom_types).tolist()\n",
"atom_types = np.array([[elems.index(i) for i in atom_types]])\n",
"atom_types = atom_types.repeat(len(qm_coord), axis=0)\n",
"\n",
"energy = np.array((np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy.npy\", \"rb\")) - np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy_sqm.npy\", \"rb\"))) * 27.2114 * 23.061, dtype=\"float32\")\n",
"energy = energy - energy.mean()\n",
"qm_gradient = np.array((np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad.npy\", \"rb\")) - np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad_sqm.npy\", \"rb\"))) * 27.2114 * 23.061 / 0.529177249, dtype=\"float32\")\n",
"\n",
"device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')\n",
"\n",
"qm_coord = torch.from_numpy(qm_coord).to(device)\n",
"atom_types = torch.from_numpy(atom_types).to(device)\n",
"energy = torch.from_numpy(energy).to(device)\n",
"qm_gradient = torch.from_numpy(qm_gradient).to(device)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"id": "5fc0zx5YOn-y",
"colab": {
"base_uri": "https://localhost:8080/"
},
"outputId": "3a6bbd16-ac1c-47d3-99fb-75011e5df388"
},
"outputs": [
{
"output_type": "stream",
"name": "stderr",
"text": [
"INFO:lightning_fabric.utilities.seed:Global seed set to 2\n"
]
}
],
"source": [
"pl.seed_everything(2)\n",
"dataset = TensorDataset(qm_coord, atom_types, energy, qm_gradient)\n",
"train, val = random_split(dataset, [2016, 84])\n",
"# Training Set Size: 2016 (96%)\n",
"# Test Set Size: 84 ( 4%)\n",
"# Data Set Size: 2100\n",
"train_loader = DataLoader(train, batch_size=32)\n",
"val_loader = DataLoader(val, batch_size=32)"
]
},
{
"cell_type": "markdown",
"source": [
"## Using ANI for Feature Extraction\n",
"\n",
"Here we set the parameters for the ANI model and begin training our BP-FNN."
],
"metadata": {
"id": "L-g9rxO6LSu5"
}
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"id": "0FYCh2Le7jRr",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 306
},
"outputId": "6af9d322-d0f6-41d4-c2d9-4b99008fc1b4"
},
"outputs": [
{
"output_type": "stream",
"name": "stderr",
"text": [
"INFO:lightning_fabric.utilities.seed:Global seed set to 2\n",
"INFO:pytorch_lightning.utilities.rank_zero:GPU available: True (cuda), used: True\n",
"INFO:pytorch_lightning.utilities.rank_zero:TPU available: False, using: 0 TPU cores\n",
"INFO:pytorch_lightning.utilities.rank_zero:IPU available: False, using: 0 IPUs\n",
"INFO:pytorch_lightning.utilities.rank_zero:HPU available: False, using: 0 HPUs\n",
"INFO:pytorch_lightning.accelerators.cuda:LOCAL_RANK: 0 - CUDA_VISIBLE_DEVICES: [0]\n",
"INFO:pytorch_lightning.callbacks.model_summary:\n",
" | Name | Type | Params\n",
"-------------------------------------------\n",
"0 | descriptor | FeatureANI | 0 \n",
"1 | fitting_net | Fitting | 383 K \n",
"-------------------------------------------\n",
"383 K Trainable params\n",
"0 Non-trainable params\n",
"383 K Total params\n",
"1.532 Total estimated model params size (MB)\n",
"INFO:pytorch_lightning.utilities.rank_zero:`Trainer.fit` stopped: `max_epochs=100` reached.\n"
]
}
],
"source": [
"%%capture\n",
"%%time\n",
"pl.seed_everything(2)\n",
"\n",
"ani = True\n",
"\n",
"if ani:\n",
" # From TorchANI\n",
" Rcr = 5.2000e+00\n",
" Rca = 3.5000e+00\n",
" EtaR = [1.6000000e+01]\n",
" ShfR = [9.0000000e-01,1.1687500e+00,1.4375000e+00,1.7062500e+00,1.9750000e+00,2.2437500e+00,2.5125000e+00,2.7812500e+00,3.0500000e+00,3.3187500e+00,3.5875000e+00,3.8562500e+00,4.1250000e+00,4.3937500e+00,4.6625000e+00,4.9312500e+00]\n",
" Zeta = [3.2000000e+01]\n",
" ShfZ = [1.9634954e-01,5.8904862e-01,9.8174770e-01,1.3744468e+00,1.7671459e+00,2.1598449e+00,2.5525440e+00,2.9452431e+00]\n",
" EtaA = [8.0000000e+00]\n",
" ShfA = [9.0000000e-01,1.5500000e+00,2.2000000e+00,2.8500000e+00]\n",
" EtaR, ShfR = np.array(np.meshgrid(EtaR, ShfR)).reshape(2, -1)\n",
" Zeta, ShfZ, EtaA, ShfA = np.array(np.meshgrid(Zeta, ShfZ, EtaA, ShfA)).reshape(4, -1)\n",
" EtaR = np.repeat([EtaR], 3, axis=0)\n",
" ShfR = np.repeat([ShfR], 3, axis=0)\n",
" Zeta = np.repeat([Zeta], 3, axis=0)\n",
" ShfZ = np.repeat([ShfZ], 3, axis=0)\n",
" EtaA = np.repeat([EtaA], 3, axis=0)\n",
" ShfA = np.repeat([ShfA], 3, axis=0)\n",
" descriptor = FeatureANI(Rcr, EtaR, ShfR, Rca, Zeta, ShfZ, EtaA, ShfA)\n",
"else:\n",
" Rcr = 6.0\n",
" Rca = 6.0\n",
" ShfR = np.zeros((3,6)) # H, C, O\n",
" EtaR = [0.0, 0.04, 0.14, 0.32, 0.71, 1.79]\n",
" EtaR = np.repeat([EtaR], 3, axis=0) # H, C, O\n",
" Zeta = [1, 2, 4, 8, 16, 32, 1, 2, 4, 8, 16, 32]\n",
" Zeta = np.repeat([Zeta], 3, axis=0) # H, C, O\n",
" EtaA = [0.0, 0.04, 0.14, 0.32, 0.71, 1.79, 0.0, 0.04, 0.14, 0.32, 0.71, 1.79]\n",
" EtaA = np.repeat([EtaA], 3, axis=0) # H, C, O\n",
" LamA = [1, 1, 1, 1, 1, 1, -1, -1, -1, -1, -1, -1]\n",
" LamA = np.repeat([LamA], 3, axis=0) # H, C, O\n",
" descriptor = Feature(Rcr, EtaR, ShfR, Rca, Zeta, EtaA, LamA)\n",
"\n",
"fitting_net = Fitting(3, descriptor.output_length, neuron=[240, 240, 240])\n",
"model = BPNN(descriptor, fitting_net, learning_rate=5e-4)\n",
"csv_logger = pl_loggers.CSVLogger('logs_csv/')\n",
"trainer = pl.Trainer(max_epochs=100, logger=csv_logger, log_every_n_steps=20, accelerator='auto')\n",
"trainer.fit(model, train_loader, val_loader)\n",
"model.to(device)"
]
},
{
"cell_type": "markdown",
"source": [
"## Saving the Model with PyTorch Files and Evaluating the Model's Accuracy Using RMSD"
],
"metadata": {
"id": "OkKS46hBwoEi"
}
},
{
"cell_type": "markdown",
"source": [
"### Saving the Model with PyTorch\n",
"\n",
"The following files are saved:\n",
"\n",
"**1) model.pt**\n",
"- torch.save saves tensors to model.pt\n",
"\n",
"**2) model_script.pt**\n",
"- torch.jit.save attempts to preserve the behavior of some operators across PyTorch versions.\n",
"\n",
"Previously saved models can be loaded with:\n",
" - model.load_state_dict(torch.load(\"model.pt\"))\n",
" - torch.jit.load(\"model_script.pt\")"
],
"metadata": {
"id": "UoCqvOvdLZ6H"
}
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"id": "wDsRamgOkdXY"
},
"outputs": [],
"source": [
"torch.save(model.state_dict(), 'model.pt')\n",
"torch.jit.save(model.to_torchscript(), \"model_script.pt\")"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"id": "cRMmWy9TPeJD"
},
"outputs": [],
"source": [
"ene_pred, grad_pred = model(qm_coord, atom_types[0])"
]
},
{
"cell_type": "markdown",
"source": [
"### Plotting RMSD for $\\Delta$MLP Energy and Forces\n",
"\n",
"RMSD for predicted and reference energy and forces are calculated and displayed below."
],
"metadata": {
"id": "qnQCBYPZL7eF"
}
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"id": "JlF1V44dPibM",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 506
},
"outputId": "d302ce14-9d13-4bec-fdb8-adb38f037330"
},
"outputs": [
{
"output_type": "display_data",
"data": {
"text/plain": [
""
],
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA94AAAHpCAYAAAB0jeQXAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAD4g0lEQVR4nOzdd3SUVbfH8e9MCJ0EQknAACIgIL0TkNACiFKko3QBQcUrRUGwggUVpNkQRZoiVRAQ6RGkGuCNoIJShUgTIhMIEEIy949xxkwySWYmZVJ+n7WyVuape7jv9WQ/zzl7G8xmsxkRERERERERyRBGTwcgIiIiIiIikpMp8RYRERERERHJQEq8RURERERERDKQEm8RERERERGRDKTEW0RERERERCQDKfEWERERERERyUBKvEVEREREREQyUB5PB5AdxMfHc/78eYoUKYLBYPB0OCIiks2ZzWauX79OmTJlMBr1DDwzaCwXEZH05sp4rsTbCefPn6ds2bKeDkNERHKYc+fOERgY6OkwcgWN5SIiklGcGc+VeDuhSJEigOUf1MfHx8PRiIhIdhcVFUXZsmVt44tkPI3lIiKS3lwZz7N14v36668zadIku21VqlTh2LFjANy+fZuxY8eydOlSYmJiaN++PR9//DH+/v4u3cc6Jc3Hx0eDtYiIpBtNec48GstFRCSjODOeZ/uFZdWrV+fChQu2n127dtn2jR49mnXr1rFixQp27NjB+fPn6datmwejFRERERERkdwmW7/xBsiTJw8BAQFJtptMJubNm8eSJUto3bo1APPnz6datWrs27ePJk2aZHaoIiIiIiIikgtl+zfex48fp0yZMtx333307duXs2fPAnDw4EFiY2MJCQmxHVu1alXKlSvH3r17U7xmTEwMUVFRdj8iIiIiIiIi7sjWiXfjxo1ZsGABGzdu5JNPPuH06dM0b96c69evc/HiRfLmzUvRokXtzvH39+fixYspXnfKlCn4+vraflQFVURERERERNyVraead+jQwfZ7rVq1aNy4MeXLl2f58uUUKFDA7etOmDCBMWPG2D5bq9WJiIiIiIiIuCpbv/FOrGjRotx///2cOHGCgIAA7ty5w7Vr1+yOuXTpksM14Qnly5fPVvU0I6ufnjlzBoPBYPfj7e3NPffcQ69evThw4IDD8wYNGmQ7/sMPP0z2+r1797Ydt2DBArt9ZrOZL7/8ktatW1O8eHHy5s2Lv78/devW5emnn2bHjh12x7/++ut2cXp5edn+vXv27Mn8+fOJjo5O87+J1c6dO3n++edp1aoVvr6+GAwGBg0a5PJ1jh8/zttvv01wcDBlypQhb968lC1blgEDBtiq3zty6NAhevbsSYUKFShQoADly5enS5cu7Ny5M8mx+/fvZ+DAgdSoUQM/Pz/y589PpUqV6N27d7L/NxQRkZxD43ny0ms8Txy3o58hQ4YkOW/jxo2EhIRQtGhRChQoQM2aNZk+fTpxcXFJjv3hhx9SvH7if3sREVdk6zfeid24cYOTJ0/Sv39/6tevj7e3N9u2baN79+4A/P7775w9e5agoCAPR2qvYsWK9OvXD4Do6GgOHjzIihUrWLNmDVu3biU4ONjheXny5OGLL75g5MiRSfZFRkby7bffkidPHu7evZtk/xNPPMGCBQsoVqwYHTt25J577uHWrVv8/PPPzJs3j6ioKFq0aJHkvO7du1OjRg3AMhPgzJkz/PDDD6xcuZJXX32VxYsX07JlyzT8a1h88cUXLFy4kIIFC1KuXDm319m/8sorLFu2jBo1atClSxd8fHw4cuQIixcvZuXKlWzcuDHJv++aNWvo3r07+fLlo2vXrpQtW5Zz586xevVq1q5dy/z58+3+aPjxxx/ZsmULTZo0oXXr1hQsWJBTp06xdu1aVqxYwcKFC+nfv39a/jlERCQb0HieVHqN5ynF8vnnn/PXX3/Rvn17u+2zZ8/mueeew8fHh27dulG0aFG2bt3K2LFj2bt3LytWrHB4vRYtWji8X506ddyKXUQEAHM2NnbsWPMPP/xgPn36tHn37t3mkJAQc4kSJcyXL182m81m84gRI8zlypUzb9++3XzgwAFzUFCQOSgoyOX7mEwmM2A2mUzpGv/p06fNgLl9+/ZJ9k2ZMsUMmIODg5PsGzhwoBkwd+rUyQyYw8PDkxwza9YsM2Du3LmzGTDPnz/ftm/nzp1mwFynTh2H3+mff/4x7969227ba6+9ZgbMX3/9dZLjb9++bX7nnXfMRqPRXKhQIfPPP//szNdPUVhYmPmXX34x371717x3714zYB44cKDL15k/f7750KFDSbZ//fXXZsD8wAMPJNlXrVo1s8FgMP/vf/+z237w4EGzwWAwV6hQwW77rVu3HN77yJEj5vz585tLlSpljo+Pdzl2Ecm5MmpckeRl5L+5xvPkpdd4npyLFy+a8+TJYy5evLg5JibGtv2vv/4y58uXz1ysWDHzmTNnbNtjY2PNXbp0cfhvEBoaagbMr732WrrFJyI5mytjS7aeah4REcFjjz1GlSpV6NWrF8WLF2ffvn2ULFkSgBkzZtCxY0e6d+9OcHAwAQEBfPPNNx6O2jnW6VIHDx5M9piBAwfi5eXFvHnzkuyztk5z9HbfWtV94MCBDqfRFy1alKZNmzoda758+Rg/fjyvvvoq0dHRvPjii06fm5wGDRpQvXp1vLy80nSdQYMGUbdu3STb+/Tpw/33389vv/3GlStX7PadOnWK0qVLJ3myXa9ePUqXLs3ff/9ttz1//vwO712jRg2qVavG5cuXVRlfRCSX0niePuN5chYuXMjdu3fp378/efPmtW3//vvviYmJYejQoZQvX962PU+ePEyaNAmATz75JENiEhFxJFsn3kuXLuX8+fPExMQQERHB0qVLqVixom1//vz5+eijj4iMjCQ6Oppvvvkm1fXdWU2ePMmvBrjnnnto164dS5Ys4c6dO7bthw4dIjw8nMGDBzs8r3jx4gD88ccf6Rrr2LFjKViwIJs2bcJkMtm2W9dMpceUtfTk7e0NJP03rlGjBhcuXCA8PNxu+6FDh7hw4QJt2rRx6vonT57k999/p2zZsvj6+qZLzCIikj1pPM8Y1ocVQ4cOtdtu7WBToUKFJOdYt+3Zs4eYmJgk+48fP87MmTOZMmUKixcv5q+//krvsEUkF8rWiXdO9vnnnwPw4IMPpnjckCFDuHr1Kt9++61t27x588iTJw8DBgxweE779u3x8fFhzpw59O3bl5UrV/Lnn3+mOebChQtTv3594uPjU3yynxX89NNP/PrrrzRs2DBJy7kZM2ZQuHBhmjZtSr9+/ZgwYQJ9+/blwQcfpGXLlsyZMyfZa77++uu89NJL9OvXz/amPbnjRUQk59N4nnF+/PFH/vjjD5o0aUL16tXt9pUoUQKA06dPJznPuu3u3bucOnUqyf4lS5YwevRoJk6cyIABA7j33nsZM2aMw4JsIiLOylHF1bKrEydO8PrrrwP/FWMJDQ3F39+fqVOnpnhu586dKVGiBF988QU9e/bk9u3bfP311zzyyCP4+/s7PCcwMJBVq1YxZMgQlixZwpIlSwAoWbIkrVq1Yvjw4bRu3dqt71KmTBkAu+nbjRo14ujRoxQsWNCta6Y3k8nEwIEDMRqNvPfee0n2N2/enB9//JGePXvy1Vdf2baXL1+eQYMGJTtr4qeffrJNXwNLz/hFixbRrl279P8SIiKS5Wg8z1zJve0GaNeunW36/rPPPmtrC3v37l27sTph95uSJUvyzjvv0LFjR+69916io6PZu3cvL774IjNmzMBgMPD+++9n7JcSkRxLb7yzgJMnTzJp0iQmTZrEtGnTCA0NJSAggF27dlGtWrUUz/X29qZfv35s3ryZv/76i9WrV/PPP//wxBNPpHheSEgIJ0+eZMuWLbzyyis8/PDDxMTEsHz5ctq0acPEiRPT7fsVLFiQqlWrUq5cuXS7prtu3bpF165dOXbsGG+88YbD6XLfffcdwcHBNGzYkKNHj3Lz5k2OHj1Ks2bNGDhwIOPGjXN47ZEjR2I2m7l58yY///wzDz30EB06dGDatGkZ/K1ERCQr0HieeaKiolixYgWFCxemd+/eSfZXqFCBiRMnEhkZSc2aNXniiScYPXo09erVY/v27bbvYDT+96dw9erVGT9+PNWrV6dQoUKUKlWKLl26EBoaSsmSJZk9ezaXL1/OtO8oIjmLEu8soH379pjNZsxmM5cvX2bq1KlcvnyZzp07c+PGjVTPf+KJJ4iPj2fBggV88cUXBAQE8PDDD6d6Xp48eQgJCWHy5Ml89913XL16lc8++4w8efIwZcoUDh065PJ3OX/+PICtwF1Wcvv2bdsAOmHCBId/jFy9epW+fftSuXJlFi9eTNWqVSlQoABVq1Zl8eLF1K9fn+nTp3P27Nlk71OgQAFq1arFggULeOihhxg/fjy//PJLRn41EckkEZgI5TQRmFI/WHIdjeeZZ+nSpdy8eZPevXtTuHBhh8dMnjyZxYsXU6VKFZYuXcq8efMIDAxk9+7dtmJ0pUqVSvVeAQEBdOnShbt377J///50/R4i4hmeGM+VeGcxJUuW5Pnnn2fixIkcPXqUl19+OdVzatasScOGDfnoo4/Yvn07AwYMSLGIS3Ly5MnD0KFDefzxxwEIDQ116fwbN25w8OBBvLy8qFevnsv3z0i3bt2ic+fObNmyhXHjxvH22287PG7Pnj2YTCZatGhh9xQcLE/Fg4ODiYuL4/Dhw07dt127dsTHx/Pjjz+m+TuIiGfN4xDlYqbRmoWUZybzcD2ZkdxD43nGsq6ddzTNPKF+/fqxf/9+bt68SVRUFBs2bKBSpUocP36c4sWLOyy+5oh1zXh0dHTaAhcRj/PUeK7EO4uaOHEiZcqU4eOPP+bMmTOpHv/EE09w4cIF4uPjU52Wlprknhyn5v333+fmzZt06NAhS1XxvnXrFl26dGHLli08//zzvPvuu8kea60mm7hlmJV1e758+Zy6t/WNgbWCuohkTxGYGHZyIeZqH8Kq34jHzHDW6c23pErjefo7cuQIYWFhVK9enSZNmrh8/sqVK4mJiXE4RT051jfd9957r8v3E5GsIwITw8LmYK40G3adzdTxXIl3FlWgQAHGjx9PbGwsb7zxRqrH9+vXj9WrV/P9999TpUqVFI/duHEj3377LXfv3k2y78SJE6xYsQJIvQKrVUxMDO+99x6TJ0+mcOHCTJkyxW7/zZs3OXbsWIrTs9MquXtYp5dv2bKFMWPGpFrcpnHjxnh5ebFy5cokb7XDw8NZuXIlBQsWpHHjxrbtBw4ccHit8PBw5syZg7e3NyEhIW5+MxHJCn48cxhz64Vw+hpM3gl344nDzAkiPR2aZHEaz13jzD2sRdWsPdKTExUVlWTb0aNHGTt2LD4+Pkn6lCdXwX3WrFmEhoZSuXJlGjZsmNpXEJEsJuG08u8O7cTcbjFERMGUXQCZNp6rqnkW9uSTT/Luu++yaNEiJk6caNejPLHChQvz6KOPOnXdY8eOMXr0aEqUKEFwcDAVK1bEbDZz4sQJNmzYwJ07d3jqqafskkurlStXcuzYMcAyFe306dPs3LmTK1euULZsWb788ktq1Khhd85PP/1Eq1ataNGiBT/88INTMe7atcs2jcz6lnnXrl0MGjQIsEz5Sli0LLl7jBgxgi1bthAQEECRIkVs1WYTGjRokO0JdmBgIOPHj+ftt9+mYcOGdO3alfLly3PmzBnWrFnDnTt3mD17tm1tGECPHj3IkycP9evXp1y5cty5c4fff/+dLVu2YDabmTVrlp6Qi2Rj586d48XW/eGsCe4vDpv6QR4jXhiohJ+nw5NsQON52sdzqzt37vDll1+SN2/eZNusWY0dO5ZDhw7RsGFD/Pz8OH78OOvWrcNoNLJmzRpbpXOr7t274+3tTYMGDQgMDCQ6Opp9+/bxv//9j6JFi/Lll1/i5eXl1PcWkaxhHod4knXEY8bw8yUKtF0C125Ds7KwrAdApo3nSryzsPz58zNhwgSeffZZJk2axKJFi9Llun379qVw4cJs2rSJI0eOsGXLFm7fvk2JEiVo164dgwYNonv37g7PXbVqFatWrcJoNFK4cGFKlSpFy5YteeSRR+jVq1e6tRg5ceIECxcutNt28uRJTp48CVhaezlTLdw6re/ixYt27UMSatmypV1i/NZbb1GrVi0+/fRTNm3axPXr1/H19aVVq1Y899xzdOjQwe78iRMnsn79evbt28e6deuIj4+ndOnSPP7444wcOdLhHzwikj389ddftGrVirOn/6RkxUCubu9FfEBhvDDwKZ0IJOtNw5WsR+N52sdzqzVr1nD16lV69epF8eLFUzy2Xbt2HDt2jBUrVnD9+nUCAgLo27dvsg8/nnrqKTZt2sTOnTu5evUqRqOR8uXLM2rUKMaOHUtgYKDTcYqI50VgsiXd/HoZc8gibkbepFzjB4jY0Jn4wnkzdTw3mM1mc4bfJZuLiorC19cXk8lk96ZTRERyrosXL9KiRQv++OMPKlSowI4dOzCU9eEEkVTCL02DtMaVzKd/cxGR3CWU07RmIRy7Ai0XwKVoaFCGdVs2UKfovZk+nuuNt4iISCKXL1+mdevW/PHHH5QrV47t27fbpqXqLbeIiEjWE4GJ40RS+d9kujJ+GI5HWmq0XIqGOgEYN/WjTtF7CcQ308dzJd4iIiIJXLlyhZCQEI4ePco999zD9u3bVadBREQkC0u4ltuIgbl0ouVJX4q2WsY/F25AzVIYt/Rnrl9vjz1AV+ItIiLyr8jISNq2bcuRI0coXbo0oaGhKRbCEhEREc+yW8sNxGPmyTOLKN16Ff/8dZn7H6jKO1sX0bDE/R6dtabEW0REBLh27Rrt2rUjPDycUqVKsX37dipXruzpsERERCQFx4m0Jd0AnDMR33ohf529xv3338+ObaEElArwXID/Uh9vERHJ9aKionjooYc4ePAgJUqUYPv27VStWtXTYYmIiEgqKuOHEYPlw19R0HoRnL5G+YoV2L59OwEBnk+6QYm3iIjkcjdu3ODhhx9m//79+Pn5sXXrVqpXr+7psERERMQJgfgyl04YL96wJN0nIilR4R5+DN3BPffc4+nwbJR4i4hIrhUdHc0jjzzC7t27KVq0KFu2bKF27dqeDktERERc0OlyIJXafAd/XOWecoGEbd9l60aSVSjxFhGRXOnWrVt07tyZnTt34uPjw+bNm6lXr56nwxIREREXHL5yiqCQYP747Rj33HMPO7b/kCW7kai4moiI5Dq3b9/m0UcfZfv27RQuXJiNGzfSsGFDT4clIiIiqUjYr3tV5CFGtX0cjlyE0oV5OvTDLNuNRIm3iIjkKjExMXTv3p3NmzdTsGBBNmzYQFBQkKfDEhERkQTCiOBHztKccjQkELDv182129BuEYRfhFKFYPtAXq38MwNo5dG2YclR4i0iIrlGbGwsvXv3ZsOGDRQoUIDvvvuO5s2bezosERERSWAQq1nIz7bPA6nNMzT8L+mOioGHvoSDF6BEQdg+AKqWIA4zJ4hU4i0iIuIpsbGxPPbYY3z77bfky5ePtWvX0rJlS0+HJSIiIgmEEWGXdAMs5Of/tt24Aw9/Bfv/Ar8CsLU/VC8FgBcGKuGX2SE7RcXVREQkx7t79y4DBgxg1apV5M2blzVr1hASEuLpsERERCSRHzmb/M7oO/DIEth9Dormhy39obalT7cXBj6lU5Z82w164y0iIjlcXFwcgwcPZunSpXh7e7Nq1SoeeughT4clIiIiDjSnnOMdt2Kh81LY+Sf45IPN/aBeabww8DXdCaJslk26QW+8RUQkB4uPj2fo0KF8+eWX5MmTh+XLl9OxY0dPhyUiIiLJaEggPahmv/H2XXh0GWw/DYXzwsa+0PAe21vuntTI0kk36I23iIjkUPHx8YwYMYIFCxbg5eXFkiVLePTRRz0dloiIiKRgHof4hmP/bYi5C92Xw+aTUNAb44a+vBv0BA0oQyX8snzCbaXEW0REchyz2cyzzz7LZ599htFoZPHixfTs2dPTYYmIiEgKIjD9V7kcIDYOeq+EDcehQB6e+W4GLzbvl22S7YSUeIuISI5iNpsZPXo0H3/8MQaDgfnz5/PYY495OiwRERFJRgQmjhPJ30TbJ92PrYJvf4d8XhjXPsaLLbNn0g1KvEVEJAcxm82MGzeOWbNmAfD5558zYMAAD0clIiIiVtYku/K/08Tnccj+LTfA3XgYsAZWHYW8XhjW9GFuyKhsm3SDEm8REckhzGYzL7/8MtOmTQNgzpw5PPHEEx6OSkRERKwSJtkGYCSN+Igw+6Q7Lh4GfwtLfwFvIx1WTWTuQ2OzddINSrxFRCSHmDx5Mm+//TYAH3zwAcOHD/dwRCIiImKVeP22GfiAn+wPijfDsHXw5WHIY4TlPRnXcXC2T7pB7cRERCQHePvtt3n99dcBmD59OiNHjvRsQCIiImLnOJH2b7YTizfDU+thfjh4GWBJN7werUYl/DItxoykxFtERLK1qVOn8tJLLwHw7rvvMnr0aA9HJCIiIolVTimBNpvh2Q0w9xAYDbCoK149a/ApnXLE227QVHMREcnGZs6cybhx4wB44403bL+LiIhI1hKIL32pyVccsd9hNsPoTfDxATCAYX4Xlj0+iSDK5pikG/TGW0REsqmPPvrI9nb71Vdf5eWXX/ZwRCIiIpKSOgTYbzCbYfxWmLXf8vnzzpgH1OYnzidJuiMwEcppIjBlUrTpS2+8RUQk25k7d65tHfeECRNs67tFRETEcxK3Cku4rTDejGfrfwebzfDydpi6x/J5ziPwRF0AprOH52hsu0bCauhGDMylE0Ool6nfLa30xltERLIsR0+3v/jiC1vF8rFjx/LWW29hMBg8FaI4YefOnXTq1IkyZcpgMBhYs2aN3X6z2cyrr75K6dKlKVCgACEhIRw/ftzumMjISPr27YuPjw9FixZlyJAh3LhxIxO/hYiIpGQehyjPTFqzkHLM4AU2M5Xdtm2N+dy+uNrkHfD2LsvvH3SA4Q1su+KBE0QCSauhx2NmOOuy3ZtvJd4iIpIlJRzAyzOTeRxi8eLFDB06FIDnnnuOqVOnKunOBqKjo6lduzYfffSRw/3vvfces2fPZs6cOezfv59ChQrRvn17bt++bTumb9++/Prrr2zZsoX169ezc+dOnnzyycz6CiIikgJHrcKmsYdxbLHbZvP2j/D6Dsvv09vByEZ21/PCYKtm7qgaehxmW2KeXWiquYiIZDmOnm4P+/ptDINWYzab6fxUX8bOeF1JdzbRoUMHOnTo4HCf2Wxm5syZvPzyy3Tp0gWARYsW4e/vz5o1a+jTpw9Hjx5l48aNhIWF0aCB5Y3IBx98wMMPP8y0adMoU6ZMpn0XERFJKtVWYQlN3Q0vbbf8/m4IjA6y220Au2rmlfHDiMHu+gkT8+xCb7xFRCTLSTKAr/wNc/9viI+Ph6H1WPthRe41zGIehzwXpKSL06dPc/HiRUJCQmzbfH19ady4MXv37gVg7969FC1a1JZ0A4SEhGA0Gtm/f7/D68bExBAVFWX3IyIiGcOaHKdq5j4Y9+867zdawbhmdrsNwH6G2q3fDsSXuXTC69/re2HIlm3GlHiLiEiWUxm//4bvb4/BY6sgzgyD6sCnHcFoyLZrvMTexYsXAfD397fb7u/vb9t38eJFSpUqZbc/T548+Pn52Y5JbMqUKfj6+tp+ypYtmwHRi4iItXhaN6qlfOBHP1nahgG8GgwvByc55DM605DAJNuHUI8zjCKUgZxhVLYrrAY5LPF+5513MBgMjBo1yrbt9u3bPPPMMxQvXpzChQvTvXt3Ll265LkgRUTEeev/gJ4r4G489K0Jn3cC439P1LPjGi/JHBMmTMBkMtl+zp075+mQRERynKnspiwzaM1CVvKbw2MeoTI9596Ckd9bNkx4EF5vmeS40TROMaEOxJeWVMh2b7qtckziHRYWxqeffkqtWrXsto8ePZp169axYsUKduzYwfnz5+nWrZuHohQRkdREYGI5v2LedAK6L4fYeOhdHRY8itHLy+7Y7LjGS+wFBFh6uiZ+KH7p0iXbvoCAAC5fvmy3/+7du0RGRtqOSSxfvnz4+PjY/YiISPqZxm7GsSXV4777Yjkrhr9n+TA2CN5qDQ5qtNxP8fQOMUvJEYn3jRs36Nu3L5999hnFihWzbTeZTMybN4/p06fTunVr6tevz/z589mzZw/79u3zYMQiIpJYBCZeYDPlmMHYbXPg0WVwJw66V4PFXfHK48W7hGT7NV5ir0KFCgQEBLBt2zbbtqioKPbv309QkKXgTlBQENeuXePgwYO2Y7Zv3058fDyNGzfO9JhFRLIzR6063bmGM0k3i3+GoWstvz/XGKa2dZh0A3SkitvxZAc5oqr5M888wyOPPEJISAhvvvmmbfvBgweJjY21K9hStWpVypUrx969e2nSpInD68XExBATE2P7rIIsIiIZax6H/qti/sMZ6PQ13L4LnavAku54eefhUzoxhHr0oQYniKQSfkq6s4kbN25w4sQJ2+fTp08THh6On58f5cqVY9SoUbz55ptUrlyZChUq8Morr1CmTBkeffRRAKpVq8ZDDz3EsGHDmDNnDrGxsYwcOZI+ffqoormIiAsSjrdGDMz9d2xNjXUdd+V/x97jRKZew/zrIzDoW0sfsacawIz2YDBgxMCLPMgUfsSMpaDaZ3TO8WN6tk+8ly5dyqFDhwgLC0uy7+LFi+TNm5eiRYvabU9YsMWRKVOmMGnSpPQOVUQkx0s8MKd2DMAezv2XdO86Cx2XwK278HBlWN6Dp/M2YRC1bcVWAvHN8YNzTnPgwAFatWpl+zxmzBgABg4cyIIFCxg3bhzR0dE8+eSTXLt2jQcffJCNGzeSP39+2zlfffUVI0eOpE2bNhiNRrp3787s2bMz/buIiGRXjlp1Dmcd7amY4rjqKFn3Sq2C+crfoP9qiDfD0Lrw4cO2N93xmGnLfTxFg1z1ID1bJ97nzp3jueeeY8uWLXaDc1pNmDDB9kcBWN54qxqqiEjKnHmKnvAY65Bte2K+LwI6fAXRsdD2PljVC/Ll4WPCmMMBp5/KS9bTsmVLzObk340YDAYmT57M5MmTkz3Gz8+PJUuWZER4IiK5gqNe29YipSk9LE+crA9jbcpvu5N0I7EvjGqtz5LbHqRn6zXeBw8e5PLly9SrV488efKQJ08eduzYwezZs8mTJw/+/v7cuXOHa9eu2Z2XsGCLIyrIIiLimuSeoidcP5b4GDMJku4D56H9l3DjDrS6F9b0gfz/PRtW6zAREZG0cdRrO7UipY6S9RST7u9S7kYC0I9auSrhtsrWiXebNm04cuQI4eHhtp8GDRrQt29f2+/e3t52BVt+//13zp49ayvYIiIiaZfSU/SUjgHgfxeg7WKIioHg8rDuMSjoneQwtQ4TERFxXyC+dtPEnSlS6ihZT9amE9DNvhtJDS//JGd/yeFc+SA9W081L1KkCDVq1LDbVqhQIYoXL27bPmTIEMaMGYOfnx8+Pj48++yzBAUFJVtYTUREXGcdmBMm1omfojs6hsOXIGQxXLsNTcvC+segUF6H91DrMBERkbQZQj3aU9HptdXWZH0464hL6V33tlP/dSPpZulGQh4jv/J3krNSm96eU2XrN97OmDFjBh07dqR79+4EBwcTEBDAN9984+mwRERyFGefog9LuEb718vQZhFE3oJG98D3faFIPofXV+swERGR9BGILy2p4PSYOoR6TCEk+QN2nPmvG0mn++Hr7uDtBTielp5bH6QbzClVOxHAUlzN19cXk8mk9d4iIimIwOTwKbpduzCAY1eg5QK4FA31S8PWAVDUvkimEQPvEEJDyuS4iqcaVzKf/s1FRNwTgYlyzHD8vnvXWXjoS0th1IcrwzeWwqiJWWe8WR+k55Riqa6MLdl6qrmIiGQtjiqUJi6qxvGr0HqhJemu7Q+b+ydJug3APobYWoiJiIiIZ/RgueOkO5luJIl5YWAvQ4gmNsc9SHeFEm8REclQdkXVTv0DrRfBhRtQo5TlTbdfgSTnvEdbJd0iIiIeFIGJF9nKfv5KujOFbiSWYmxm4rEk3aMJojRFcm3CbZXj13iLiIhn2Sqi/nkNWi2EiCioVgK2DYASBZMc/xLNeZ5mmR+oiIiIEIGJF9hMWWbwFUeSHpBKN5J4zCylB8/TlHjMTGMP5ZnJPA5l4rfIepR4i4hIhonAxB7O8di5spak+6wJ7i9uSbpLFUpy/HDq8yZtPBCpiIiIzOMQ5ZnJNPY4PsCJbiReGLiXokxnr22KejxmhrMuV7YRs9JUcxERyRDzOMQw1mI+fx1aL4DT16BiMdg+AEoXSXK8FwZeJjjT4xQRERHLw/JhrE2+aZgT3UisxdNuEGvfPpTc20bMSom3iIiku/X8zlDWwsUblkJqJyLh3qKwfSDck7Tqp9qFiYiIeNYs9iefdB+7Ykm6r9y0dCPZ1A98krYA/Zru9KQGEZhslcytcmsbMSsl3iIikmYRmDhOJJXx42W2s5Cf4XK0ZZD+/SqU9YHQgVAuaWI9g/b04AEl3SIiIpnIOnYXxpvTXEt+erkT3UjAklgHURawdDmZSyeGs464BG3EcvNYr8RbRETSJGGPbtvT7as3IWQR/PY33FPEknTfWzTJuV4YlHSLiIhksoRjd4qc7EZihCSJ9RDq0Z6KnCAyV7cRs1LiLSIibkvcozseM/xzy1Lt9MhlKF3YMr28YtKpZUYMvENIrh+IM0poaCjbtm1j9+7dREREcOXKFQoWLEjJkiWpWbMmLVq0oGPHjgQEBHg6VBERyUSJx+5kOdGNxAiMoSnP0djheB6Ir8b5fynxFhERt9n16AZLldN2X8L/Llqqlm8bYKli/i8jBrpRjVX8RjxmxrOVYhRgCPU8EH3OEx0dzezZs/nss8/4888/MZst/7fJnz8/fn5+3Lp1i19++YXDhw/z1Vdf4e3tTadOnRg9ejTNmqmFm4hIbpBk7HbknCnVbiS9qc402imxdpLaiYmIiNtsPbrB0s+zw1dw4Lzlifi2AVCtpO1YI/AtffiGo2ovkgHmzJlDpUqVeOmll/Dx8eGNN95g27ZtmEwmbt68SUREBFevXiU2NpZjx46xcOFCevXqxebNmwkODqZbt26cPn3a019DREQymN3Y7cj565bp5al0I2lB+YwLMgdKl8TbZDIRGxubHpcSEZFsIIwIprOHcC7yGDXgxh14+CvYFwHF8sPW/pa1YP/ywsBcOlOIvMm2F5G0efbZZ2nbti2HDx8mPDyciRMn0qpVK4oUsf9jyWAwcP/999O/f38WL17MpUuX+PTTT/n5559ZvHixh6IXEZGMEIGJUE7bHnBbC6r1oJrjE5zsRgLwNBsoz0zmcSiDos9ZXJ5qfuPGDVasWGFbN3b+/Hnu3r0LQJEiRahZsyYtW7akS5cuNGjQIN0DFhERzxrEakvVcqubsdBxCew+B775YEt/qP3fuuGEVcsjMGEAu9Q7t7cXSS+//vor999/v8vnFShQgKFDhzJ48GDOnj2bAZGJiEhGSNhRxNF074QF1AxAdx7gG44mP838b+e6kSRknbnWnoqacp4KpxPvc+fO8eabb/L1119z48YNAIoVK0bFihVt68YiIyPZt28fu3fv5u2336ZOnTqMGTOGvn37ZtgXEBGRjGcd3KO5Y59034qFzl/Djj8t/Tw394f6ZWy7E1ct38RJu+saSFoFVdzjTtKdkJeXFxUqVEinaEREJCMl7igyl0529VISF1AzAyv5LfkLXr0JIYtT7UbiiHXmmsbylDmVeL/44ovMnj2buLg4OnToQK9evQgKCnI4QN+8eZODBw+yefNmlixZQv/+/ZkxYwafffYZdevWTfcvICIiGWsquxnPlqTPx2/fha7LYNtpKJwXvu8Lje6x7U6cVFv/CEh4HSMG2lMxo7+CiIhIjuGoo8hw1lGLUpzmmu24VAuoWVm7kRy+BAHJdyMxAG/RmpfYrplrbnAq8Z4zZw7PP/88o0aNws8v5X/UggUL0rx5c5o3b84bb7zB1q1bmTx5MuvWrVPiLSKSzUxjN+PYknTHnTjosRw2nYSC3rDhcWha1u4QQ6Kk2lEVVT0lz3zHjx8nPDzc9vPzzz8TERHh6bBERMRJyY2njfnc2VT7P6ZE3Ui223cjSegzOjOEepSiMMNZRxxmvDBo5pqTnEq8T58+TbFixdy6QUhICCEhIfzzzz9unS8iIp4RgYnxbE26IzYOeq+E745DgTyw/jFonrSyaXyipNpaRTXhHwt6Sp42Bw8e5NVXX+XkyZM0aNCAqVOnUrp0aQBiYmJshdasP0eOHCE6OhrA1mrMYEihsq2IiGQ5jsZTwPWkOyoGHkq+G0lCn/CwbSr7EOrRnoqcIJJKyawvl6ScSrzdTbrT+xoiIpJ5HPb5vBsPj38Da45BPi/4tg+0crwuOHFSHYgvc+mkp+Tp5NSpU7Rq1YoWLVrw1ltvMX/+fNq0aUPdunUJDw/n+PHjxMXFAdj18zabzVSvXp0hQ4ZQvXp1atSo4cmvISIiLko8nhqBeFcvkko3koQMQEeqJIlB47drXK5qLiIiucNqjtpviIuH/qth5W+Q1wtW94a2ya/P7ka1JIOynpKnn/Xr1xMdHc2XX36Jr68vbdq0wc/Pj99//x2j0UilSpWoUaMGNWrUoGbNmtSoUYOKFSvi7e1NUFAQo0aN8vRXEBERNyUcT7dyirf40fmTU+lGkthYmmq8TgdOJd47d+50+wbBwcFunysiIp4RRgQf8NN/G+LiYfC3sPQX8DbCyp7QoXKK11jBb0xlNy/QzG67npKnjzJlymA2m9mzZw8dOnRgz549gGXq+HPPPcekSZMoVKiQh6MUEZH05KiFWBsWOX+BVLqRONKLB9ISsvzLqcS7ZcuWbq8Bs05zExGR7GFq4oJq8WYYtg4WHwYvAyzrAZ2qJH+BBF5kC49RQ4l2BujevTudO3emU6dOlC9fHrPZzHvvvcf777/PjBkzWLJkCZMnT2bIkCFaxy0ikgM4aiF2jCvOVy9PpRtJcqKJTWPkAk4m3q+++qoGbRGRHC4CE2+yk085+N9GsxmeWg/zw8FogCXdoWs1p68ZD6pankEMBgNr1qwhLCyMS5cu0bx5c3x9fRkxYgRvvfUWM2fOZPjw4cyePZtp06bRrl07T4csIiJuSq6FWJyzSbcT3UgcURHU9ONU4v36669ncBgiIuJJ09jNC4nbhpnN8Oz3MPeQJele3BV6VXfpuhqwM17Dhg3tPhcuXJgpU6YwYsQIxo0bx4oVK+jQoQPt2rVj6tSpHopSRETSIrkWYk5xshtJYiqCmr6Mng5AREQ8a2pySfeYTfBRmKWc6Red4fGaqV7rYSrZBhYN2J5Vvnx5li1bxq5du2jQoAGbNm2ibt26msEmIpKNRGBiOb9wjL8xYv/fby+c+O+5C91IwJIcvkdbQhnIGUbZWohJ2qW5qvnu3bsJDw8nKioKHx8f6tSpQ7NmzVI/UUREPC6MCPv13GBJusdvhZn7LZ8/6wQD66R4HSMG3iWE52lGBCZVLc9CmjZtyv79+/nqq6+YMGECERERLF26lMqVKzN69Gjy5FGDExGRrGgehxjGWrv32tb+3V4YqEMAB7mQ/AVc7EYCsI+hNCQwfb6A2DGYrc09XbRnzx4GDx7MiRMnAEuPUOtT9MqVKzN//nyCgoLSL1IPioqKwtfXF5PJhI+Pj6fDERFJF0mKqIEl6X4lFN76ty3JJ4/AiAaA5cX3cOozl0O2wi4TeJDa+GMGmlJWibaTPDWu3L59m6lTpzJ16lSio6OpUqUKs2bNom3btpkWg6doLBeR7CQCE+WZmWR6uQFYRg+iiWUw3yZ/AWs3ksWHIY8RvunlVGHU5fSgJzXSGH3u4crY4lbi/euvv9K4cWNu3rxJ27ZtadWqFaVLl+bixYuEhoayefNmChcuzL59+3jggexffl6DtYjkNA7XdANM3gGv/WD5ffZD8Gxju92hDKQSfrY32ps4maTCqqalpc7T48rFixeZOHEiixZZWtDcvXs302PIbJ7+NxcRcUUop2nNQof7elGd5fya/MnxZhi2Fr4It3QjWd4TujlXGNUAfEZnjeVOcmVscWuN9+TJk7lz5w4bNmxg06ZNvPjiiwwcOJDx48ezceNGNmzYwO3bt5k8ebJbX0BERDJOBCbHSfeUH/9Lut9vlyTpBjjAeQLxpSWW9WGOKqxGYMqo0CUVH3/8MX/99VeqxwUEBPDFF18QFhZGcHBwJkQmIiKuqIxfkjXdVikm3WYzPP2dJem2diNxMukGMIPG8gziVuL9ww8/0KNHDx566CGH+x966CF69OhBaGhomoITEZH09398n3TjtD0wcbvl93fawBjHS4VeZKttME6uwuoJItM1XnHeyJEjKVeuHA0bNuStt97iyJEjKR5ft25dtm/fnknRiYiIswLxZS6dkk2+HbJ2I/n0oOXVdSrdSAzAKJI+ZNdYnjHcSrxNJhMVKiRfDQ+gQoUKmEx6UiIikpX0ZDmrOWa/cdY+eOHfN+CTW8L4B5M9P+Fg7OhpvNqHeVZYWBgTJ07kzp07vPLKK9SpU4eKFSsyduxYduzYQXx8vKdDFBERJw2hHn8yik94mCapFTxL3I1kfpdUu5F8RmfG0lRjeSZxK/EuU6YM+/btS/GY/fv3U6ZMGbeCEhGR9BWBiU/4iZX8Zr/j4zAYtcny+yvB8EqLFK+TeDAeQ5CtnYnah3le/fr1eeONN/j55585deoU06ZNo1y5csyePZvWrVvj7+/P4MGDWbNmDTdv3vR0uCIikoqv+YWn2cA+IpI/yGyGF13rRvI2rRlCPdubdY3lGc+txLtz58788MMPvPLKK9y+fdtu3+3bt3nttdcIDQ2lS5cu6RKkiIi4LgIToZxmGrspxwyeZoP9AXMPwjP/bnuxGUxqmeo1pxBCIL7M4xDlmck09hCPmedpqn6fWcy9997L6NGjCQ0N5dKlS8yfP5/mzZuzcuVKunXrRokSJejUqRNffPEFly9f9nS4IiKSyLR/u4+kWAnb2o3kvT2Wz588AkNSH4v7U9v2+xDqcYZR6t2dwdyqan716lUaN27M6dOnKV68OI0aNcLf359Lly4RFhbG33//zX333cdPP/2En1/2n6agSqgikt3M45Bd4bMk5v8Pnlhr+X1ME5jWDgypryOzVjVP3OLECwNnGKUn5E7y5LgSExPDli1b+Pbbb1m/fj2XLl3CaDTSpEkTdu3alamxZCaN5SKSnURgoiwzUj8wlW4kjnyuquXpxpWxJY87NyhevDj79u1j3LhxLF26lA0b/nuLkj9/fgYPHsy7776bI5JuEZHsJgJTykn3l4dhyL9J9/81cjrptk4zT6momhLvrC9fvnx07NiRjh07Yjab2bt3L99++y1r1671dGgiItlSBCaOE0ll/NI8DlqvtZezqR/sRDeSxNSn23PcSrwBSpQowRdffMGnn37KsWPHiIqKwsfHh6pVq+Lt7Z2eMYqIiBOsg/XfRCefdC/9BQausfQLeaoBzHzIqaQbIIT7bH9QGDEkeeOtQizZj8FgoGnTpjRt2pR3333X0+GIiGQ7CWeYGTEwl05uv02eym7Gpza13MrJbiQJGYEgyroVm6Sd24m3lbe3NzVrplwxT0REMlbigd+hVb9Bv28g3gxD68KHDzuddANs4SQRmGyFWIazjjjMKsSSRTzxxBNunWcwGJg3b146RyMikvMlnmEWj5nhrKM9FVMcExO+Ib/AdX7kLL9wmfmEO3djF7qRWBmAuXTWWO1BaU68RUTEsxwN/Aawf2L+7THoswrizDCwNnzaCYwu9AYF4sE2nXwI9WhPRU4QSaV0mFonabdgwQK3zlPiLSLiHneWXqVagyU1LnYjeY1gqlOKIMpqrPYwtxPvXbt2MW3aNH7++WfOnz/P3bt3kxxjMBgcbhcRkfTjaOC3+/TdH9BzBdyNt/T0nNfZ5aQbkk4nD8RXg3gWcvr0aU+HICKSq1TGz6WlV6nWYEmNi91IjMBQ6musziLcSrwXL17MoEGDMJvN3HfffTRq1Ig8efTyXEQks0VgSrkAy6YT0G05xMZDr+qw8FHwcr2TpKaTZ33ly5f3dAgiIrmKq0uvHD0od9r8/8Hw9ZbfxzSBt9ukuFxMU8uzHrey5TfeeINixYqxYcMGGjVqlN4xiYiIE1KdrrbtFDy6DO7EQdeq8GVXyJM06U4yLT2B4dSnDzU0nVxERMQBV5ZeOXpD7pSE3UieTbkbiQH4mIfpSBWN21mM6689gHPnztGnTx8l3SIiHpLqdLUdZ6DT13D7LnS6H5b2AG+vJIcZgB484PASRuBlgmlJBQ3e2dju3bsZNmwYDRs2pEqVKjRs2JAnn3wyR/fsFhHJTIH4OjVWBuJLf2q5dvGE3UhG1IdZKXcjMQNVKalxOwtyK/EuX748d+7cSe9YXPbJJ59Qq1YtfHx88PHxISgoiO+//962//bt2zzzzDMUL16cwoUL0717dy5duuTBiEVE0keK09V2n4VHlsCtu9ChEqzoCXmTJt1gGaC/4ajDfe/QVgN3Njd69GiCg4OZN28eBw8e5MSJExw8eJDPP/+cFi1aMGbMGE+HKCKSK0RgYjm/sJCfnT8pcTeSjx5JtRuJ2ntmXW4l3sOGDWP9+vVERkamdzwuCQwM5J133uHgwYMcOHCA1q1b06VLF3799VfA8gfHunXrWLFiBTt27OD8+fN069bNozGLiKSHaJJ5+LkvAjp8BdGx0PY++KY35Et5VVFcMgl8Q8qkNUzxoIULFzJr1iwqV67MV199ZSuEeuHCBZYsWcL999/PrFmzWLRokadDFRHJcSIwEcppIjAxj0OUZya9Wen8BdzoRqJ6LFmbwWw2u7XC/5lnnmH79u28/PLL1K5dGx8fH4fHlStXLk0BusrPz4+pU6fSo0cPSpYsyZIlS+jRowcAx44do1q1auzdu5cmTZo4fc2oqCh8fX0xmUzJfk8Rkcwyjd28wJakOw6ch5BFYIqBVvfC+sehoHeq13O0xtsLA2cYpcE7g2TGuNKkSRPOnz/PkSNH8PVN+n9Hk8lEzZo1KVOmDPv27cuQGLISjeUiklmmsZvxbLW194Tka6k4tOE4PLrUUhj18Zqw6NFUC6MagP0MpSGB7gUtbnFlbHG7FHm9evVYsmQJAwYMSPaYzGwnFhcXx4oVK4iOjiYoKIiDBw8SGxtLSEiI7ZiqVatSrly5VBPvmJgYYmJibJ+joqIyNHYREWdEYOJNdvIpB5Pu/N8FaLfYknQ3LwfrHnMq6QbHfwy8Q4iS7mzu119/ZejQoQ6TbgBfX1+6d+/O559/nsmRiYjkXFPZzbgED8ddfsO5+SR0W+ZyNxIzEE2sq3eTTORW4v3BBx8watQovL29adWqFaVLl/ZYO7EjR44QFBTE7du3KVy4MKtXr+aBBx4gPDycvHnzUrRoUbvj/f39uXjxYorXnDJlCpMmTcrAqEVEXJNiBfMjl6DtYvjnNgQFwnePQ6G8qV7TCAyjvsNEvoGmmecKhlTWCoqIiPMiMDHe0Yw0Z207BV2WQkzK3Ugc0drurM+tbHnGjBncc8897Nmzh8BAz05nqFKlCuHh4ZhMJlauXMnAgQPZsWNHmq45YcIEu4IzUVFRlC1bNq2hioi4JcUK5r/9DW0WwdVb0Oge+L4vFMmX4vWMwFJ6EITlv2ufccju2hq8c4bq1auzatUq3njjDQoXLpxk//Xr11m1ahXVq1f3QHQiIjnPcSLd7dLtdDcSR4ygtd3ZgFvF1S5evEj37t09nnQD5M2bl0qVKlG/fn2mTJlC7dq1mTVrFgEBAdy5c4dr167ZHX/p0iUCAgJSvGa+fPlsldKtPyIinpJsBfPfr0DrhfD3TahXGjb1A9/8KV7LCwNz6UxPahCIL4H4MpdOeP27Ck2FWXKO4cOHExERQVBQEKtWreLKlSsAXLlyhZUrV9K0aVMiIiJ46qmnPBypiEjOUBk/3JpH5EI3ksSGU58/Gc0Q6rlzZ8lEbr3xrlSpUpKENquIj48nJiaG+vXr4+3tzbZt2+jevTsAv//+O2fPniUoKMjDUYqIOCcCE8f4O+mOE5HQehFcioba/rClPxRNOekG2MuQJIVXhlCP9lTkBJFUwk9Jdw4xePBg/ve///Hhhx/Sq1cvAIxGI/Hx8QCYzWaeffZZBg4c6MkwRURyjEB8GUtTprHH+ZPc6EaSUJ9/H6RL1udW4j169GjGjh3Ln3/+Sfny5dM7JqdNmDCBDh06UK5cOa5fv86SJUv44Ycf2LRpE76+vgwZMoQxY8bg5+eHj48Pzz77LEFBQS5VNBcR8ZR5HGIoa5PuOP0PtFoI569D9ZKWpNuvgFPXTK7wivXtt+Qss2fPpmfPnixYsIDw8HCioqLw8fGhbt26DBw4kObNm3s6RBGRHKUF5Z1PvA+ch4e+hOt3LN1I1vSB/M6nZ1oalr24lXhXrFiRFi1a0KBBA0aNGpViO7Hg4OA0BZiSy5cvM2DAAC5cuICvry+1atVi06ZNtG3bFrCsRTcajXTv3p2YmBjat2/Pxx9/nGHxiIiklwhMDHOUdP95zZJ0R0RB1RKwbQCULOTUNY0aoHOl5s2bZ/kE+/XXX09S1LRKlSocO3YMgNu3bzN27FiWLl1qN577+/t7IlwRETsRmDhOJAc5b1fRPEVudiOxtgDV0rDsx60+3kajEYPBgPXUlKqixsXFuR9dFqHenyKS2ZbzC71Zab8xIgpaLIBT/0BlP9gxCEoXcfqaI6jPJ3RKst36B0NlTTPPNBpX7L3++uusXLmSrVu32rblyZOHEiVKAPDUU0/x3XffsWDBAnx9fRk5ciRGo5Hdu3c7fQ/9m4tIRpjKbsazxbWiakcuWR6iX71l6UayqV+qhVGHU5+XsbzQ1NKwrCPD+3i/+uqrakEiIpJBIjCxh3P2G89ftxRSO/UP3FcMtg90KekGOMqVJNsStikzYmAunVSgJYeJi4sjIiKC8+fPExvreKlBRs5Oc1aePHkcFj81mUzMmzePJUuW0Lp1awDmz59PtWrV2Ldvn5aPiYjHTEvUs9spbnQjmUpbnqeZ7bMS7uzJrcT79ddfT+cwREQkAhOz2J90bdilG5ZB+ngk3FsUQgdCoOtv7HbwJ2FE2IqrJW5TFo+Z4ayjPRU1qOcA8fHxvP3228yaNYvIyMgUj80Ks9OOHz9OmTJlyJ8/P0FBQUyZMoVy5cpx8OBBYmNjCQkJsR1btWpVypUrx969e5NNvGNiYoiJibF9joqKyvDvICK5RwQmXnA16XajG4kRSwE1yf6cTrzHjRtH165dVRFcRCQDJHzzbOfvaEv18mNXoKwPbB8A5dxPindzzpZ4O2pTFoeZE0Qq8c4BJkyYwNSpUylVqhSDBw+mdOnS5Mnj1vP2DNe4cWMWLFhAlSpVuHDhApMmTaJ58+b88ssvXLx4kbx581K0aFG7c/z9/bl48WKy15wyZUqSdeMiIunFYfHTlLjZjSQeNC7nEE6PwNOnT+f999+nZMmSdOrUiS5dutC2bVvy5Ut5aoSIiKQsjAiGsTbp+rCrNyFksWVaWpkilunlFYo5dc1W3EsoZ5Jsb0ZZ2++V8cOIwS75VoXUnGPhwoVUqVKFsLAwChcu7OlwUtShQwfb77Vq1aJx48aUL1+e5cuXU6CAcxX7E5swYQJjxoyxfY6KiqJs2bIpnCEiuZE7dU7CiGATJ52/SRq6kWhczjmMzh544cIF5s6dS6NGjViyZAldunShRIkSdO/enUWLFnH16tWMjFNEJEeaxm4a83nSpPufW9B2MRy+BAGFLW+6Kzk/8O7gDD15wG7bQGrb9fAOxJe5dMILS80OVUjNWW7cuMEjjzyS5ZNuR4oWLcr999/PiRMnCAgI4M6dO1y7ds3umEuXLjlcE26VL18+fHx87H5ERBKaxyHKM5PWLKQ8M5nHIafOW8cfzt8kDd1INC7nLE4n3iVLlmTIkCGsXbuWK1eusHLlSrp3787OnTsZNGgQpUuXpmXLlsycOZNTp05lZMwiIjnCVHbzgqNKqKbb0P5L+N9FKFnQMkhXKeHSteOB8hS129ac8kmOG0I9zjCKUAZyhlEqrJaD1KpVi/Pnz3s6DLfcuHGDkydPUrp0aerXr4+3tzfbtm2z7f/99985e/aslr+JiNuSq3MSgSnF8+ZxiDfY6eRNoizTy/80WbqRbB8A/qk/DB1MHY3LOZBb7cQSio+PZ9euXaxZs4a1a9dy6tQpDAYDDzzwAF27dqVz5840aNAgveL1CLUgEZH0ZK1anqRdGMD1GGj3JeyLgOIF4IdBUKNUutzXCwNnGKUn51lAZowr3333HT179mTXrl3Uq5e1/3B7/vnn6dSpE+XLl+f8+fO89tprhIeH89tvv1GyZEmeeuopNmzYwIIFC/Dx8eHZZ58FYM+ePalc+T8ay0UkoVBO05qFDrYPpCUVHJ4TgYlyzHCuddj569BygaUw6n3FLC1AnSyM+hrBvE5rp44Vz8rwdmIJGY1GgoODCQ4OZvr06fz666+sWbOGb7/9lrfeeou33nqLMmXKcO7cudQvJiKSwyVbRA3gxh14eIkl6S6WH7YOSLekG1Q4Lbd55JFHWLBgAR06dKBz587Url072T8KBgwYkMnR2YuIiOCxxx7j6tWrlCxZkgcffJB9+/ZRsmRJAGbMmIHRaKR79+7ExMTQvn17Pv74Y4/GLCLZm6t1TiIwMZZNziXdaexGMomdlKWo3nbnMGl+452S8+fP8+2337J27Vq+//77jLpNhtNTchFJK+tb7sdY5TjpvhkLjyyBH86Abz7L9PL6ZdI1Br3xzjoyY1yJiYlh6NChLFmyBOtQbzAY7I4xm80YDIYs0U4so2ksF5HE5nGI4awjDrNtPbU12U1YdG0TJ52vYv53tGVN969/W7qR7BjkdGHUhDRmZw+Z+sY7JWXKlOGpp57iqaeeysjbiIhkaSm+5Qa4FQtdllqS7iJ5LX090yHpNmIAzMSjAi250ZgxY/jqq6+oVasWPXr0yNLtxEREPGEI9WhPRU4QSaUEVc1THbeTY+1G8qvr3UgS0yy1nMepEXjnTicLCDgQHBzs9rkiItldBCbHrcKsbt+Fbsth6yko5A0b+0HjwOSOTpGjRNvRHxSSO6xYsYL69euzd+9eJdwiIskIxNdufExcdM1paehGYp2LlPCOaiOW8zg1Erds2TLJ9DRn5YbpayIiCVmnlQNs53TyQ/edOOi5AjaegILesKEvNHWtz7Al1U450VbCnTvdvn2bVq1aKekWEXHBcSJdT7rT0I3EAHxGZ4Ak0941fucsTo3Gr776qtuJt4hIbjKPQym/4baKjYM+K2H9H5A/D6x7DIKTtvtKTifu5xWCKU0RJdriUP369Tlx4oSnwxARyVYK4+3aCddjoMNXEHbe0o1k+0B4oKTTpy+jBz2pAaBZajmcU4n366+/nsFhiIhkTwmLrwA8ybrUk+678dD3G1h9DPJ5wbd9oLXj1iWJWd9wf8dxulCVhgRqcBaH3n77bdq0acP69evp2LGjp8MREcny5nHI+SJq8F83kr3udSPxwkAQ/810SzztXXIWzT8TEXFTwuIrRgyMISj16Wlx8TBgNaz4DfJ6wTe9oV1Fp+9pvXo8ZoazjvZU1CAtDm3ZsoWWLVvSpUsXWrdunWw7MYPBwCuvvOKBCEVEsgbrEjGXku6bsdDpa9h11tKNZEt/qBPg9OmaTp77ZGg7sZxCLUhEJLEITJRnZpL+n/GYk0+94+LhibWw6GfIY4RvekGnKmmKI5SBtMS5t+WSdWTGuGI0Gp06Tu3ERCQ3c6uC+a1Y6LzUUhi1SF5L0u1kYdSRNKI71TSdPIfIlHZi169f58MPP2Tr1q2cP3+emJiYJMcYDAZOnjzp7i1ERLIsR8VX4jDzPE2Zzt6kA3i8GZ5cZ0m6vQywrIfLSbd1mrmVKp5KSkJDQz0dgohIluZWBfM0diOpQ4AemOdSbiXef//9N02bNuXkyZP4+PjYMv07d+5w69YtwNLD29vbxeIEIiLZRGX8MP77htvKCwPP0ZhePMASjjCT/ZYdZjM8/R18EQ5GA3zVDbpVc+l+BuA92vIiW1XxVJzSokULT4cgIpKluVzBPB26kTzJWi0Ty6Wcm4eWyOuvv87JkydZtGgR//zzDwCjR48mOjqa/fv306hRI+69915+/fXXdA1WRCSrCMSXuXTC69/um9ZEeBMnaczn9kn3/30Pnx60ZM+LHoXeNVy+33u05XmacYZRhDKQM4xiCPXS7wtJjvDxxx/z119/eToMEZFsobIrs8bS2I3EKh44QaTL50n251bivWHDBtq0aUO/fv2StBlr2LAh33//PWfOnGHSpEnpEqSISFY0hHp2iXAtStm3EjObYexm+DDMknR/0QX61nLrXg0oA1gS/pZU0JNycWjkyJGUK1eOhg0b8tZbb3HkyBFPhyQikiVZu5L0pWbqB6ehG0liRtAysVzKrcT7woUL1K1b1/bZy8vLNsUcoFixYnTo0IHly5enPUIRkSwsEF8q4ccs9tOIz+2T7he3wox9ls9zO8GgOm7dQ2u5xVlhYWFMnDiRO3fu8Morr1CnTh0qVqzI2LFj2bFjB/Hx8Z4OUUTEoyIw8QKbKcsMWrOQr0jlAWUau5EYEv3+Dm05TiQRmNyKX7Ivt9Z4+/r6Ehsba/tcrFgxIiIi7I7x8fHh0qVLaYtORCSLS7bn56uh8N4ey+8fPwxDXZsWbi2kprXc4or69etTv3593njjDc6cOcPq1atZu3Yts2fPZubMmfj5+dGxY0e6dOlCu3btKFiwoKdDFhHJNC5XMLd2I/n6F0s3khU94eHKTt/PCwN7GcIZrgHwJybGs9XWhnQunbRsLBdxq51YUFAQAQEBrF69GoD27dvz888/8+uvv1K8eHFu3bpF7dq1MRqNHDt2LN2DzmxqQSKSe1l7ewI0pawtAbZu783KpCdN3gGv/WD5fdZD8H+NXbrne7TlMWpwgki1G8mhMntciYyMZP369axZs4YtW7YQHR1N/vz5adOmDV27dqVjx46UKlUqw+PwJI3lIrmbozagKYo3w7C1lsKo1m4k3R9w+n7WB+fWxDq5NqRnGKVxPhvL8HZi7dq1Y8aMGdy8eZOCBQsyfPhwevToQe3atQkKCuLQoUOcOXOGt956y60vICKSFczjkN2abQPwLm25TDTvs8fx0D3lx/+S7mltXU66p/5bRA3QQCzpxs/PjwEDBjBgwABiYmLYsmUL3377LevXr+e7777DaDTSpEkTdu3a5elQRUTSjXUdd2X8XKtg7qgbiQtJ93J6EJTgYT0k34b0BJEa73MJt954X7hwgZ07d9KmTRtKlCgBwPvvv8+bb76JyWSiQIECPP3007zzzjt4eXmle9CZTU/JRXKfCEyUY4YrTUbg/T3w/BbL71PawIsPunxfPf3OHbLKuGI2m9m7dy/ffvsta9eu5ejRox6LJaNllX9zEckcCaeVGzHQjWqs5LfUT7R2I7EWRl3c1aXCqO/Rlhf+fYCekN5450yujC1uJd7JiYuL48qVK5QqVSpJtfPsTIO1SO4Tymlas9D5E2bvh+c2Wn6f1BJedb+H8nJ60BPXW45J9qFxJfPp31wk93Dr4Tn8141kxr7/upG4UBjVAJxldLKJ9DwOMZx1xGFOMhVdsqcMn2qeHC8vL/z9/dPzkiIiHlEZP1uBs1R9EvZf0v1y8zQl3QC9WUkUdzQYi0ueeOIJt84zGAzMmzcvnaMREfGcWex3L+mesC1N3UjMkOLU8SHUoz0VVcMll3Lrjffu3btZtWoV48aNIyAgIMn+CxcuMHXqVHr16kWTJk3SJVBP0lNykdwp8Rpvhz47CE+ut/w+vpllirkLM34m0px32UVcorto+lnOlhHjitHoVodQDAYDcXFx6RJDVqaxXCR3cLmImtUr2+HNHy2/f/wwPNXQ5Xtr7M59MvyN9/Tp0zl8+DDTp093uL906dKsX7+ev/76i2XLlrlzCxERj0hYiMX6ZHov57jKTZ5ig/3BC8Jh+L9J9+gmLifdA6nNW7ShNv5JqqOr4Iq46vTp054OQUTE41wqomb1xo7/ku5ZD7mddKv9p6TErcQ7LCyMNm3apHhMcHAwW7ZscSsoERFPSFyIxdpfsye+hJIoqfnqMDzxrWVe2bON4P12TiXdPahGWXx4jJo0JJAITABJprV7YaASfun23STnK1++vKdDEBHxuPfZ49oJ7+yCV3+w/O5GN5Ll9KAkhTR1XFLlVuJ9+fJl7rnnnhSPCQgI4PLly24FJSKS2SIw2ZJugHjMDGcdRchLU8rar/le9gsMWGP5MKK+5em4E0m3FwZm8JBtYE6Y6Bv4L/nWU3MRERHXhRHBdxx3/oT391jWdYNl1trYpi7dzwtDkrZhIslxK/EuWrQoZ8+eTfGYP//8k8KFC7sVlIhIZkuuv2ZvVmLEwGPUsOz95ij0/QbizTCkLnz0iFNJtzFRMp040bcm3F/TXYO4pDtr15GYmBiH+8uVK5fJEYmIpL8fSTk/sTN7/38tQCe1dLkFqB6Si6vcSrybNGnC6tWrOXfuHGXLlk2y/+zZs6xZs4bWrVunOUARkcxQGT+MGByuC4vHzFccgbW/Q++VEGeGAbUtFU+Nzq3p3scQGhJo+5xcol+SQhrEJd0cPHiQiRMnsnPnTu7cuePwGIPBwN27dzM5MhGR9BWBids4+d+yNHQj6UE1nqGRppaLy9wqgTpmzBhu3rxJs2bNWLRoERcuXAAs1cwXLlxIs2bNuHXrFmPHjk3XYEVE0lsEJtv67bl0wotkEukNx6HHcrgbD4/VgC86O510A0QTa/fZmugnpHXdkp7Cw8Np3rw5e/fupV27dpjNZmrVqkW7du0oUaIEZrOZFi1a0L9/f0+HKiLiFusY/jLbKMcMXmJ76id9dhCe/rdY6rimMLmV0/cbTWNW0JuWVFDSLS5z6413cHAw06dPZ+zYsQwePBiwPDG3diYzGo3MmjWL4ODg9ItURCSdJS6m1p9aSdp6AbD5JHRbBrHx0PMBWNQVvJx/bmmEJAl1IL7MpRPDWUccZk1Zk3T3xhtvALB//36qVauG0Wika9euvPrqq7aH4ytXruSLL77wcKQiIq5LOIY7LXE3kndCXOpG8hg1XQtSJAG3Em+A5557jlatWjFnzhzCwsIwmUwULVqURo0aMWLECGrUqJGecYqIpKsITHY9uuMxs5Cfkx64/TR0WQoxcfBoVfiqG+SxT7pr4896HmcW+5nmoJrqGJo6TKit7cpOEKkpa5Ludu3aRefOnalWrZptm/UBeYECBfjwww/Zs2cPEydOZMmSJZ4KU0TEZWFE2I3hTknYjWRkQ6e7kVg9TGW7JWMirnI78QaoVasWH3/8cXrFIiKSoRL26J7F/tQH7J1/Qqev4fZd6Hg/LOsB3l5JDjvMJQCeozHT2Wv39N0LA8+RfGuSQHyVcEuGMJlM3HfffbbP3t7e3Lhxw/bZaDTSsmVLvv76a0+EJyLiFuubbpeS7oTdSIbXh9kdXEq6m3AP39HXxUhF7Lm1xnvPHuf6482YMcOdy4uIpLt5HKI8M2nNQsoxI/U+n7vPwsNfwc1YeKgSrOwJeZMm3WAZx08QaZs+bl0nrunj4kmlSpXin3/+sX0OCAjg+HH7Nju3b9/m5s2bmR2aiIhbEncEcUribiQfO9eNxMoArKCX68GKJOJW4t2pUyeOHj2a4jEzZ87k+eefdysoEZH05Kh1V4pD9v4I6PAVRMdCyH3wTS/Il/IEoUJ4A5bp42cYRSgDOcMohlAvfb6EiIseeOABfv/9d9vnZs2asXnzZvbu3QvA0aNHWb58OVWrVvVUiCIiLnHUESRFaehGApYH6J/RWQ/QJV24lXgXKFCAhx56iL/++svh/tmzZzNmzBiCgoLSFJyISFpFYGI5vzo/UB84D+2/hOt3oOW98G0fKOCd6mkJq5YH4quKp+JxjzzyCDt37rR1Hhk/fjxms5kHH3yQkiVLUrNmTa5du8bEiRM9HKmIiHMK451c75Gk0tiNZBSN2csQPUCXdONW4r1x40aioqJo164dkZGRdvs++OADRo0aRZMmTdi4cWO6BCki4g7r9PKxbHbuhPCL0G4xmGLgwXKw7jEomHrSbSBp1XIRTxsxYgR//fUXxYsXB6B27dps27aNhx56iBIlShASEsK6devo2rWrhyMVEUlZBCZeYDON+dy5x+hp7EYCMJP9NGEe8zjkVswiibmVeNeoUYN169Zx5swZOnbsyK1btwD48MMPee6552jUqBGbNm2icOHC6RpsYlOmTKFhw4YUKVKEUqVK8eijj9pNqwPL+rVnnnmG4sWLU7hwYbp3786lS5cyNC4R8TyX14EduQQhi+Cf2xAUCBseh8J5nTp1As2TvN229haNwORq6CLpwtvbG39/f/Lm/e9/x02bNuW7777j6NGjbNy4kUceecSDEYqIJM86jv4fGyjLDKaxx7kR3YluJM6Kx8xw1mksl3Th3v8KgQcffJCvv/6asLAwevTowaxZs/i///s/GjRowKZNmyhSpEh6xunQjh07eOaZZ9i3bx9btmwhNjaWdu3aER0dbTtm9OjRrFu3jhUrVrBjxw7Onz9Pt27dMjw2EfEsl9aB/fY3tFkEV29BwzLwfV8oks+pU2tSirdoY7ctYSG38szU03IREREXJBxHP+An5090shuJK+Iwc4LI1A8USYXBbG3q6aZ58+YxbNgwDAYD9erVY9u2bfj4+KRXfC75+++/KVWqFDt27CA4OBiTyUTJkiVZsmQJPXr0AODYsWNUq1aNvXv30qRJE6euGxUVha+vLyaTyWPfTUScY20ZVhhv56ak/X4FWi6EizegXmnY2h+KFXD6fl4YOMMo2xvvCEyUZ2aSlmIJjxHJjHFl9+7drFq1inHjxhEQEJBk/4ULF5g6dSq9evVyejzMzjSWi2QPjsZRp+w5Z1kuFv1vN5I1vVMtjGoVQgWeowm3iKUPqzSGi9NcGVuc+l/jzp07k91XuXJlOnfuzK5du3j55ZcJDw+32x8cHOzMLdKFyWSZBuLnZ1lrefDgQWJjYwkJCbEdU7VqVcqVK5di4h0TE0NMTIztc1RUVAZGLSLpxdrbMx4zBlKpXA5wIhJaL7Ik3bX8YXM/l5Ju+O9JuHVAdvSmPfExIplh+vTpHD58mOnTpzvcX7p0adavX89ff/3FsmXLMjk6ERHHXK5cDpZuJA996VI3koTm86htjI7iDsNZRxxmtQWVdOXU/yJbtmyJIZV+d2az2eEU7ri4OPcic1F8fDyjRo2iWbNm1KhRA4CLFy+SN29eihYtanesv78/Fy9eTPZaU6ZMYdKkSRkZroikowhM7OEcw1hrG6pTHbJP/wOtF8L561C9pOVNd/GCLt/bC4NdYbXK+GHEkORpuYqvSWYLCwujTZs2KR4THBzMli1bMikiEZGURWDiGH+7dtJB97qRJJTw4fgQ6tGeipwgkkr4KemWdONU4v3qq6+mmnh72jPPPMMvv/zCrl270nytCRMmMGbMGNvnqKgoypYtm+brikj6S/iW22lnTZY33eeioGoJ2DYAShZy6/7vEGI3KAfiy1w66Wm5eNzly5e55557UjwmICCAy5cvZ1JEIiLJm8chuwfoTgm/CG1d70aSkJGknUkC8dW4LenOqcT79ddfz+Aw0mbkyJGsX7+enTt3EhgYaNseEBDAnTt3uHbtmt1b70uXLjlc72aVL18+8uVzrrCSiHiOy5XLASKioNVCOHMNKvtZkm5/9zswjGcrxShg1+dTT8slKyhatChnz55N8Zg///wzwzuQiIikJgITQ1nr2kkJu5E0ca0biZUBmEtnjdOSKdyuap4VmM1mRo4cyerVq9m+fTsVKlSw21+/fn28vb3Ztm2bbdvvv//O2bNnCQoKyuxwRSSdubwO7MJ1y/TyU//AfcVg+0Aok7YODMm1GgnEl5ZU0GAuHtOkSRNWr17NuXPnHO4/e/Ysa9asoWnTppkcmYiIvVnsd+2ExN1INjrfjQSgHzVZTg/OMtruwblIRnIq8U7Ynstd6XGNxJ555hm+/PJLlixZQpEiRbh48SIXL1609RX39fVlyJAhjBkzhtDQUA4ePMjgwYMJCgrKFRVcRXIqa2/PwnhjxMllMJduWKaXH4+E8r6wfQAEOlfZOLV7qNWIZEVjxozh5s2bNGvWjEWLFnHhwgXAUs184cKFNGvWjFu3bjF27FgPRyoiuVUEJpbzC++zx/mTfr9iSbr/vgl1A2BTP/DN79J9h1CPntTQw3HJVE5NNa9QoQIvvPACTz/9NIUKubYOcu/evUyaNIlmzZrxyiuvuBVkcj755BPAUvwtofnz5zNo0CAAZsyYgdFopHv37sTExNC+fXs+/vjjdI1DRDJPwjVgBqAHD7CC31I+6e9oyyB97Iol2d4+EMoXdep+RmAfQ4gmlkJ4c4Zr9Gal3Xt2FU+TrCg4OJjp06czduxYBg8eDIDBYMDaRdRoNDJr1qxM7T4iImLlVo2WxN1ItrjWAhQsD9M1ZosnONXHe9SoUXzyySfkzZuXbt260aNHD5o0aULJkiWTHHv37l1+/vlntmzZwldffcVvv/3GAw88wPz582nQoEGGfImMpt6fIllDBCbKMcO1witXb1oG6cOXLNPKdwyCSs4PuO/RlhdoZrdtHoeSFE/TVDVxRWaOK4cPH2bOnDmEhYVhMpkoWrQojRo1YsSIEbYuILmBxnKRrMOtXt2n/4EWCyyFUauXhNCBLhdGNQCf0VljtqQbV8YWpxJvgOPHj/PGG2+wYsUK7ty5A8A999yDv78/RYsW5fbt20RGRnL69GliYmIwm8088MADjBkzhkGDBmE0Zt/l5BqsRbKG5fxCb1Y6f8I/tyBkMRy6AP6FLEl3lRIu3TOUgbSkQpLtEZhUPE3clpXGlbi4OLy8vDwaQ2bISv/mIrldKKdpzULnTzhrsiTdZ65ZupH8MNClwqhNCaQ/tehIFY3Zkq5cGVuc7ixfuXJlFi1axMyZM1myZAnbtm1jz549HDx40HaMt7c3NWrUoEWLFnTt2pXmzZu7/y1EJFeLwMRxIqnsbmJrum3p63noApQsaJle7mLSndJ0NLUakazuo48+4plnnknxmLi4OPr06cOKFSsyKSoREajsylTvNHYjMQLL6KkxWzzO6cTbys/Pj5EjRzJy5EgAYmNjuXr1KgUKFMDXV/+DFpG0S7juy4iBuf9O5a5AUecucD0GOnwFYeeheAHLIP1A0qUxqXk3UY9ukezk//7v//D396dHjx4O98fHx9OnTx+++eabTI5MRHIr60P1bZxy7oQ0diNRuzDJSlxOvBPz9vZOsSe2iIgrEvfmtrbrak9FTnMt9QtE34FHlsDeCCiWH7YOgJr+LsVgAN6lLc8nWtstkp08+OCD9O/fn+LFi9OqVSu7ffHx8Tz22GOsWrXK9iBdRCQjuVxMLQ3dSACGU5+XCVbSLVlG9l14LSI5kqPe3HGY6c/q1Nd334yFjl/Dj2fBNx9s7g91XHswaMTAfoYmKagmkt2sW7eO+++/n65duxIeHm7bHh8fT9++fVmxYgVPP/00s2fP9lyQIpIrJH6onqo0dCMBywN0Jd2S1SjxFpEspTJ+Dvtm/8CZlE+8fRe6LIUfzkCRvJa+ng3KuHx/M2YOc9nl80SyGh8fHzZt2kSxYsXo0KEDp06dwmw28/jjj7Ns2TJGjBjBhx9+6OkwRSSHi8DEWDY7n3RfvWkpjPrr35Zp5aEDLdPMXWAGThDperAiGUiJt4hkKYH4MpdOeDlIvpMVcxe6LoOtp6CQN3zfFxoHunV/MzCcdURgcut8kawkICCATZs2ERcXR7t27ejVqxfLly9n2LBhfPzxx54OT0RyuHkcojwzWc6vzp3wzy1o96WlBah/Icv0chdagFp5qVe3ZEFKvEUkyxlCPc4wiv7USv3gO3HQcwVsPAEF8sB3j0Ozcmm6fxxmPSmXHOP+++9nw4YNXL58mW+++YahQ4fy6aefejosEcnhwohgGGudf9Odxm4k1sf1Xhj4lE6aZi5ZTpqLq4mIZIRAfAkikMUcTv6g2DjosxLW/QH588D6x6HFvWm+t56US3Y0efLkFPc3atSI8PBwypQpY3eswWDglVdeyejwRCQXmcchhrHW2ZQ7XbqRLKMHJSlEJXfbkIpkMIPZbHb6/ydyK1cao4tI+onARFlmON55Nx4eXwUrfoO8XrDuMWhX0elrG7BMKzcC3ajGao4Rh9n2pHwI9dLjK4g4lBHjitHo3iQ2g8FAXFxcusSQlWksF8kcEZgoxwznk+7oO5ak+8ezlm4k2we6XBjVCwNnGKWEWzKdK2OLW2+89+/fT+PGjd0KTkQkMWtfz8rOPqWOi4eBayxJt7cRVvd2KekGS+K9jB4EUZZAfInAxAki9aRcsq3Q0FBPhyAiwjp+dz7pvhkLndLWjURTyyW7cCvxDgoKombNmgwbNox+/fpRtGjRdA5LRHKLhH09jRiY++/b5ghMdGVZ0hPizTBkLSw5AnmMsKInPFzZ5fvGAyUpZBuoA/HVoC3ZWosWLTwdgojkcvM4xNNscO7g23fh0aUQesbtbiSf8DAdqaLxW7IFt+al9evXjxMnTvB///d/lClThgEDBvDjjz+md2wiksMl7usZj5nhrGMquynPTA5w3v6EeDM8uQ4W/gxeBljaHbpUdeveWsctkj199NFH3HvvveTPn5/GjRvz008/eTokkVwtAhOhnCaMCIay1rmTrN1ItrjfjaQH1RhBIyXdkm24lXgvWrSI8+fP88EHH1C1alW+/PJLWrZsSdWqVXn//fe5cuVKescpIjnQcSKTVDuNw8x4tiStgmo2wzPfwbz/gdEAX3WD7g+4fe93CNFgLZLNLFu2jDFjxvDaa69x6NAhateuTfv27bl8+bKnQxPJlaztwlqzkEZ87txJ6dCN5FkasYLebkQs4jlutxPz9fXlmWee4dChQxw4cIAnn3ySS5cu8cILLxAYGEjv3r3ZunVresYqIjlMZfwwJurXbS16Zsdshuc2wpyDlgMWPgq9a6Tp3g1wbTqbSFb30EMPERYW5ta50dHRvPPOO3z00UfpHFX6mj59OsOGDWPw4ME88MADzJkzh4IFC/LFF194OjSRXCcCk2vtwiBpN5J1j7nVjeQjwpjHIZfPE/GkdOnjXa9ePT755BPOnz/PggULKFGiBCtXrqR9+/bcd999vPfee1y/fj09biUiOcjLbE8yYDtMup/fDB/8O510Xmfo50R/7xRomrnkRH///TdNmjShVatWzJ8/H5PJlOo5+/btY+TIkZQvX5433ngDf3//TIjUPXfu3OHgwYOEhITYthmNRkJCQti7d2+S42NiYoiKirL7EZH0s4dzrqTclm4kfb+B1ccs3UjW9IY297l1b+vStAhS/++cSFaRbn28//nnHxYtWsTnn3/O+fPnMRgMNGvWjKNHj/Liiy8yc+ZMvv32Wxo2bJhetxSRbCyMCBbyc8oHmc0wYRtM32f5PLcjDK6bpvuq+qnkVAcPHmThwoVMmjSJIUOGMGzYMKpUqUL9+vXx9/enaNGi3L59m8jISH7//XcOHDjA9evX8fLyok+fPrz55puUK+fadM/MdOXKFeLi4pI8HPD39+fYsWNJjp8yZQqTJk3KrPBEcqSUuo5c5abzF3LUjaR9pTTFFoeZE0RqPJdsI82Jd2hoKJ999hlr1qzh9u3blCxZkhdeeIHhw4dz3333ERMTwxdffMG4ceN49tln2bdvX3rELSLZRMJBGyzrugvjzXDWp37yaz/Au7stv3/0MAyr7/L9jRgYQxC9eIBoYtUuTHK0gQMHMmDAADZs2MD8+fP54Ycf+PLLL5McZzQaqVWrFl27dmXo0KGULl3aA9FmrAkTJjBmzBjb56ioKMqWLevBiESyl+S6joBlbE9SADU5aexGMpQ6PEkDmjDPbpacZq9JduNW4n3p0iXmz5/PvHnzOHXqFGazmRYtWjBixAi6deuGt7e37dh8+fLx1FNPceLEiSy/dkxE0lfCQdvh2u2UvLED3thp+X1me3ja9dkyRmAfQ2iIa5VSRbIzg8HAI488wiOPPALA0aNHiYiI4OrVqxQoUICSJUtSvXp1fH2z1wOoEiVK4OXlxaVLl+y2X7p0iYCApH1/8+XLR758+TIrPJEcJbmuI+2pyCZOOl+9PB26kbxGKwLxZS6dGM464jBr9ppkS24l3oGBgcTHx1OsWDFGjRrFk08+SZUqVVI8p2TJkty5c8etIEUk+7C+4S6MN8NYa0u2XUq639kFr/5g+X1qW3iuictxGIG5dFbSLbletWrVqFatmqfDSLO8efNSv359tm3bxqOPPgpAfHw827ZtY+TIkZ4NTiSHSa7ryF7OOZ90p0M3kvdoa0uuh1CP9lTkBJGavSbZkluJd+PGjRkxYgQ9e/Z0+mnyiy++yIsvvujO7UQkm0jTG26r6Xst67oB3m4Nzzd1+RJGDHrTLZIDjRkzhoEDB9KgQQMaNWrEzJkziY6OZvDgwZ4OTSRHsXYdSTy1+4qz67rToRvJSzTnBZrZbQvEVwm3ZFtuJd67du1K7zhEJJtLPC3NraR79n4Yu9ny++stYEJzly9hnX6mpFsk5+nduzd///03r776KhcvXqROnTps3LgxS1djF8mOHE3tfocQvud46iensRuJEXiHtkmSbpHsLt2qmotI7uZoWppLPgmzPB0HeKk5vNrC6VMfpCzTaa/iaSK5wMiRIzW1XCQdJVe5POHU7jDO8wJbUr9YGruRDKc+LxOscVxyJLcS79atW6d6jNFoxMfHhypVqvDoo4/SuHFjd24lItmEo2lpTvv8EDy9wfL7uKbwRiswGJw+fRfn2MGfPO/g6XhKrVBERERys5Qql4PlzfcFrjPOmaQb0tSNpB81mUMnF6IXyV4MZrPZ5b+SjUaj5WSDAUenJ95uMBgYPHgwn3/+eRpC9ZyoqCh8fX0xmUz4+Ph4OhyRLCvhAO60heEw+FvL3PRRjWF6e5eSbisDsJQeNKWsLcFO7Q8KEU/RuJL59G8uYi8CE+WZmWQd9xlGEYgvEZh4k518ykHnLvjGjv8Ko85s73Jh1HOM1gNyyXZcGVuM7tzg1q1bdOrUiWrVqrFkyRL+/PNPbt++zZ9//smSJUuoXr06nTt35ty5c2zevJl69eoxf/58PvnkE7e+kIhkTRGYCOU0EZgAy7S0x3CheMqSI/8l3c80dDvpBsslerOS8sxkHoeSbYVijVVERCQ3S65y+QkimcchyjLD+aT73bR1I/mczkq6JcdzK/F+7bXXOHLkCPv376dPnz6ULVuWvHnzUrZsWfr06cPevXs5fPgwH3zwASEhIWzZsoWSJUsyf/789I5fRDwgAhMvsJlyzKA1C+2S3SUcce4iy3+F/qstGfOT9WB2hxSTbmfTcWuCvYdzyf5BISIikttZl4gl5IWBQng73zIMLN1IXvy3G8lbrncj+YSHNRtNcgW3Eu8lS5bQrVs3ChUq5HB/oUKF6NatG19//TUARYsW5aGHHuLo0aPuRyoiHpcw4Z7GHltamzDZdWqS+eqj8PgqiDfDE3Xgk46WHp/JMGDp5en17x8IXhjoyQNJ/mCwivu3nZmjPygq4edMhCI5wt27d5kxYwaNGjXCx8eHPHn+K+0SHh7O008/zR9//OHBCEXEU6yVyxOOre8QwgS2OX+RDxJ1I5noWjcSA9CRKi6dI5JduVVc7e+//yY2NjbFY+7evcvly5dtn0uXLk1cXJw7txORLCC19dtxmAnldOoXWvc79F4JcWboXwvmdkox6QbLS/FY4lhCdwxA0L/ruCMwsZdz9GFVkjVqQZRN0grlUzppKpvkGrdu3aJdu3bs2bOHEiVK4OPjQ3R0tG1/hQoVmD9/Pn5+frz55psejFREPMWtyuVWcw7A/7nXjQQsSfdnmmIuuYhbb7wrVqzIihUruHr1qsP9V69eZfny5VSsWNG27fz58/j56U2TSHaUeL10cuakthbs++PQYwXExkOfGjC/C3g595+hiWynNyvpwyo2cRKwPK3vSY0kT+ytCfYQ6nGGUYQykDOM0lQ2yVXefvttdu/ezZQpU7h48SJDhw612+/r60uLFi3YtGmThyIUkawgEF8q4cd4V5Luzw/BU99Zfn/BtW4kfanJcnpwltEalyVXceuN97PPPstTTz1FvXr1GDt2LM2aNaNUqVJcvnyZ3bt38/7773Pp0iVee+01AOLj49m+fTsNGzZM1+BFJHOkuUc3wJaT0HUZ3ImDHg/A4q5OJ90JWae1t6ei7Sl5wif2ift4B+Krp+mSKy1btoxWrVoxbtw4wNJhJLH77ruP//3vf5kdmohkMceJdH6UXxgOT66z/D6qMbwb4lJh1KHUoyUVXA1RJNtzK/EePnw4f/31F1OmTGH06NF2+8xmM0ajkQkTJjB8+HAAIiMjef7552na1LViCyKSNaSpRzdA6GnovBRi4qBLFVjSDfK4NeEG+K9ImhJskeSdPXuWrl27pnhMkSJFMJlU6V8kt4rAxB7OcQLHs1iTSGM3EtVakdzMrcQbYPLkyfTv358lS5Zw+PBhoqKi8PHxoXbt2vTp04f777/fdmyJEiV47rnn0iVgEcl81gIsLlU5tdr5J3T8Gm7fhUcqw7Ie4O2Vpng0cIukrkiRIna1Vhw5efIkJUuWzKSIRCQrmcpuxrkyvdzFbiSJGVVrRXI5txLvRYsW4e/vT/v27W3TyUUkZ6tFKQzg2jvvPefg4a/gZiy0rwgre0E+t5/3AahImoiTmjRpwrp167h27RpFixZNsv/cuXNs2LAh1bfiIpLzTHM16XaxG4ljZtpTMfXDRHIot+Z6DhkyhI0bN6Z3LCKSRU1lN4353LWk+6e/4KEvIToW2lSA1b0hv/tJtwFYTg8VSRNx0gsvvMA///xDmzZt2L17N3fv3gXg5s2bbNu2jfbt23P37l3GjBnj4UhFJDNFYHIt6XajG4kj8cAJIl0+TySncOuv4NKlS9sGcBHJ2Vx+Kg5w8Dy0WwzX70CL8rD2MSjg7dIl6lOacC7atQLrSQ3X4hDJxYKDg/nwww957rnnCA4Otm0vUqQIAF5eXnz88cfUr1/fUyGKSCaLwMRcDjr/ID0N3UgS0zIxye3cSrw7d+7Mli1biImJIV++fOkdk4hkERGYGM9W1076+SK0XQymGHiwHKx/HAq6lnQDhHORvQwhmtgklcpFxDlPPfUULVu2ZM6cOezfv5/IyEh8fHxo3LgxTz/9NNWrV/d0iCKSCSIwMYv9vM8e55PudOpGApYptlomJrmdW4n3W2+9xd69e+nWrRvvvfeeBm6RHCYCE8eJ5G+iXatk/stlCFkM/9yGJoGw4XEonNetGOIwE02sWo6IpFG1atWYNWuWp8MQkUxmHcsPcJ7xbHFtuVg6dyNZSg/NWpNcz63Eu27dusTExBAeHs7GjRvJnz8/pUqVStIj1GAwcPLkyXQJVEQynltPxK2O/g1tFsGVm9CgDGzsC0XcnxGjKWkiIpLbWZPnyi7O/JrHIZ5knXttQNO5G4kXBoIo6/b5IjmFW4+u4uPjyZs3L+XKlaNcuXKUKlUKsPTwTvgTHx+frsGKSPqIwEQop4nAZPv8Apspz0ymOUi6Uy2h8sdVaL0ILkdDnQDY3A9887scl/U+qlwukna7d+9mzJgxXLx40eH+CxcuMGbMGPbt25fJkYmIM+ZxiPLMpDULKc9M5nHIqfMiMLmfdKdzNxK1EBP5j1v/n3TmzJl0DkNEMkvCp+BGDPSnFov4OcXhOcWh+2QktF4IF29AzVKwtT8UK+ByXEZgH0O1plsknUyfPp3Dhw8zffp0h/tLly7N+vXr+euvv1i2bFkmRyciKUmcPMdjZjjraE9Fh+Njwjfjx4l0L+lOYzeSxC1HLeP6EBoS6HosIjmQ+4s1soidO3fSqVMnypQpg8FgYM2aNXb7zWYzr776KqVLl6ZAgQKEhIRw/PhxzwQr4mGOBvKFqSTdKTpzDVothL+uwwMlYesAKF7QrUv1pzYNCaQlFZR0i6SDsLAwHnzwwRSPCQ4O1htvkSzIUfIch9lhO67Eb8aX8QvG1Oeq2Tt0IU3dSF6iOZ/RGa9/7+uFgbl0VtItkkCaE+/ffvuNb775hsWLF6dHPC6Ljo6mdu3afPTRRw73v/fee8yePdtW0bVQoUK0b9+e27dvZ3KkIp7n9lNwR86aLEn3uSioUhy2DYBShdy+3Jcctk19F5G0u3z5Mvfcc0+KxwQEBHD58uVMikhEnFUZvyTJs6PaJ44eqH/KQdfG+p8vQsgiSzeSZmXd6kYyggYMoR5nGEUoAznDKIZQz6VriOR0bifeYWFh1KlTh5o1a9KzZ08GDRpk27dz504KFizI2rVr0yPGFHXo0IE333yTrl27JtlnNpuZOXMmL7/8Ml26dKFWrVosWrSI8+fPJ3kzLpIbOBrI3fJXlGV6+ZlrUMkPtg+EgMJOn+4oguSe5IuIe4oWLcrZs2dTPObPP/+kcGHn/39XRDJHIL7MpZPdG2RHa6XT/EA9STeSvm51I7GO34H4auaaSDLcSrx//fVXWrduzenTpxk9ejQdOnSw29+8eXNKlCjBihUr0iVId50+fZqLFy8SEhJi2+br60vjxo3Zu3dvsufFxMQQFRVl9yOSEwTiSw+qpe0iF65bCqmd/AcqFIXtA6BMEZcuMZHmTj3JFxH3NWnShNWrV3Pu3DmH+8+ePcuaNWto2rRpJkcmIs5w5g1ymh6oO+pG4uN6NxKN3yLOcSvxfu211wA4ePAg06ZNo2HDhnb7DQYDQUFBhIWFpT3CNLBWcvX397fb7u/vn2yVV4ApU6bg6+tr+ylbVi0QJHtLWMX8edLwR/alG5ZB+o+rUM4XQgdCWdeeaj9LI96kjVNP8kXEfWPGjOHmzZs0a9aMRYsWceHCBcBSzXzhwoU0a9aMW7duMXbsWA9HKiLJSe0NsvXNuMvJdzp1I9H4LeI8t6qa79ixg+7du1OpUqVkjylXrhwbN250OzBPmjBhAmPGjLF9joqKUvIt2VbiKuZz6cRAarOQn1270JWbluloR69AoI8l6S5f1OV4uv37xn0I9WhPRU4QqSrmIhkgODiY6dOnM3bsWAYPHgxYHoybzZZpqUajkVmzZhEcHOzJMEUkjYZQjz+5xhvsdO6EdOhG8hLNCeE+jd8iLnAr8b5+/bqtd3dybt26RVxcnFtBpZeAgAAALl26ROnSpW3bL126RJ06dZI9L1++fOTL5/pUG5GsxlHRlSdZx7f0cS3xjrxlKbzyy2UoXdgyvfy+Yi7HYwS76WiB+GrAFslAzz33HK1atWLOnDmEhYVhMpkoWrQojRo1YsSIEdSoUcPTIYpIOmhEyoUUbdKpG8k77GIEDTSGi7jArcS7bNmyHDlyJMVjDh06RMWKFd0KKr1UqFCBgIAAtm3bZku0o6Ki2L9/P0899ZRHYxPJDI6KrsRjphNfO3+Ra7ctLUZ+vgT+hSyF1CoXT/U0IwbeIYTxbLFFYAY2cVKVTkUyUa1atfj44489HYaIpLOEvbt38GfqJ6RjNxJrQVQl3iLOc2uNd8eOHdm8eTNbt251uH/58uXs27ePRx99NC2xOeXGjRuEh4cTHh4OWAqqhYeHc/bsWQwGA6NGjeLNN99k7dq1HDlyhAEDBlCmTJlMiU3E09Jcxdx0G9p/CQcvQMmClkG6agmnTn2XEB6jBoYE9zcDw1mntmEimcDLy4u+fft6OgwRyQAJe3eXZQbT2JPyCWnsRpKYEQOFcK3lmEhu51biPXHiRMqUKcPDDz/MsGHDOHDgAAAff/wx/fv35/HHH+fee++1WyedUQ4cOEDdunWpW7cuYCkmU7duXV599VUAxo0bx7PPPsuTTz5Jw4YNuXHjBhs3biR/ftcLSIhkN64WXalKgqT6egw8vAR++gv8Climo1VPeYlJYo7euKttmEjm8PHxUX0SkRwmAhPL+YWhrHW+jVg6dCNJLB4zTZjHPA6l6ToiuYnBbK2y4qJTp07Rv39/h225GjduzNdff829996b1viyhKioKHx9fTGZTPj4+Hg6HBGXLeB/DOZb50+IvgMdvoIfz0LR/JZBum7p1M9LwIiBfQyhCfPs/jjwwsAZRml6muRqmTGutG/fHqPRyPfff58h189uNJZLdpewWKrTLt2wTC8/esXSjWTnILcKo1oZwO7uGtMlt3NlbHFrjTfAfffdx+7duwkPD2ffvn1ERkbi4+ND48aNk7QXExHPsK7/OsU/zp90MxY6fW1Jun3yWVqMuJh0g+VpeDSxzKUTw1lHHGa1HRHJRK+//jotW7Zk0aJFDBgwwNPhiEgaJC6W6pR06kZi1YvqLOdXu21a6y3iPLcTb6s6deqkWCFcRDxjHocYxlpXhmi4fRceXQqhZ6BwXtjUDxo6WSk1ES8MVMKPllRQ2zARD9iyZQstW7Zk8ODBfPDBBzRs2BB/f38MBvulJwaDgVdeecVDUYqIMxwt3UpROnUjsfLCQOUEXUkSbq/kYLuIJOX2VPPcRNPTJDuJwMQ6fudpNrh2Ysxd6LoMvj8BhbxhYz94sJxbMVjfbKt6uYhjmTGuGI3OlXExGAweb/+ZGTSWS3aTsGo5QHlmOpd8X7ttSboPXrB0I/lhkNOFUQGW04OdnOUjfsKMZUyfkqhLidV7tOUFmjl9bZGcJlOmmv/999/Mnz+fsLAwrl275nDQNhgMbNu2zd1biIiL3HrLDXAnDnqusCTdBfLAd4+7nHQbgXdoS0PK6M22SBYQGhrq6RBExE0J13MbMTCXTtQjgANcSPnENHQjAXiepkRxh48Jw8x/rUHL4evwb4t7NdaLOM2txPvw4cO0bt2af/75h5RemCeeziYi7kn41Du5hDYCk3tJd2wc9FkJ6/6A/Hlg3WPQ4l6nTvXCwF6GEE2skm2RLKZFixaeDkFE3JB4PXc8ZoayNvUT06EbSS8esCuKGo+ZF9nKB3Rw+XuIiD232omNHTuWyMhIXnrpJU6fPk1sbCzx8fFJfnLD1DWRjJawV2d5Ztpad0RgIpTTtp7Yx4l0Pem+Gw/9VsPqY5DXC9b0hjb3OX36aIJoSCAtqaCkW0REJB24vJ4bLN1IHlkCe85ZupFs6Q+1/F26xHDqc4NYh21AS1AwSWNSAxCEWhaKOMutN9579+7l0UcfZfLkyekdj4gk4Oip93DWEckt21orA/AubSnvauIbFw+D1sDyX8HbCN/0gvaVnD7dCDxHY9fuKSKZbvfu3SxYsIDw8HCioqLw8fGhbt26DBgwgAcffNDT4YlIIpXxw4jB+eTbUTeSeq51IzEALxMMkOTeXhgIoiyf0ZknWUs8lr8B5tJZD91FXOBW4p03b14qVqyY3rGISCKOnnrHYWYcW2yfzWD32SnxZhi6Dr46AnmMsKInPHK/06erLZhI9jB69Ghmz55tWxZmMBgwm80cPHiQefPm8dxzzzF9+nQPRykiCQXiy1w6OTe9PB26kSROopNrAzqEeupSIpIGbiXeLVq04MCBA+kdi4hgv57b5afezog3w/B1sCAcvAzwdXfoUtWpU4dSh77U1oArkg0sXLiQWbNmcf/99/Paa6/RqlUr/P39uXz5MqGhoUyaNIlZs2ZRp04d9fkWyWLaUxEDpDz6x9yFbstgyylLN5Lv+0KTQJfuM4L6vESw3ZieUoIdiK/GfxE3udVO7OTJkzRp0oTx48fz/PPPZ0RcWYpakEhmcVTFFLA9eU4zsxme2QCfHACjAb7qBn1qOH36JzzMCBqlPQ6RXC4zxpUmTZpw/vx5jhw5gq9v0j+UTSYTNWvWpEyZMuzbty9DYshKNJZLdhLKaVqzMPkD7sRBj+WWwqgF8liSbicLo1pNpDlv0SZtgYrkchneTuytt96iRo0ajB8/njlz5lCnTh2HNzIYDMybN8+dW4jkOsmt5z7DKJbQnd6sTNsNzGYYtdGSdBuABV1cSroNQEeqpC0GEck0v/76K0OHDnWYdAP4+vrSvXt3Pv/880yOTESSE4GJPZzjGb5L/qDYOHhslVvdSKym0pbn1X9bJFO5lXgvWLDA9vupU6c4deqUw+OUeIs4L7n13CeIpCll0zbl3GyGF7bA7J8snz/vDP1rO326AfhMRVREchy1/RTJPCm1Bo3AxCz28z57Uh7prd1IvjnqVjcS0Ow1EU9xK/E+ffp0eschkus5Ws/thcG2vupdQnjB1SJqYEm6J26D9/daPn/aEZ6o69IlDEmaiIhIVle9enVWrVrFG2+8QeHChZPsv379OqtWraJ69eoeiE4kd3G0lGwI9Wz7nCqklsZuJFbFKejyOSKSdm718S5fvrzTPyLiHGsVU69/k9zElcPLufu2+fUf4J3dlt8/7ABP1nf5EtZp79ae4SKS9Q0fPpyIiAiCgoJYtWoVV65cAeDKlSusXLmSpk2bEhERwVNPPeXhSEVytuSWkkVgIowI55LuNHYjsVLvbRHPceuNt4ikL+v0s/ZU5Ayj7CqJWqefTWOP6xd+cydM3mn5fUZ7eMbx1LKRNCKYclzlJk+zweE0N+u0d003F8keBg8ezP/+9z8+/PBDevXqBYDRaCQ+Ph4As9nMs88+y8CBAz0ZpkiOl9xSMuvU8lSloRtJQuq9LeJZTiferVu3ZtCgQXYtR/bv38/+/fv5v//7vyTHv/vuu7z33ntcvXo1fSIVyaFSmn42jd2MY4t7K7vf3QWvhFp+fy8ERjWx7TIAo2jM/RSnI1XsBmFv8vAka4lPdDnrtHcRyT5mz55Nz549WbBgAeHh4URFReHj40PdunUZOHAgzZs393SIIjmeo6VkRkh9PTdYlouN3ACf/8/SjeTLbtDjAZfub8TAUroTRFkl3SIe5HTi/cMPP9CyZUu7bRs3bmTy5MkOE+/bt29z7dq1tMYnkqMlN/3Mn0LMZB/bcLOewoy98OI2y+9vtYYX/qtcap3Cbk3uE7P275zFfmawlzjMSaa9i0j20bx5cyXYIh5kXUpmbQ3qdLHUNHYjsYrHTEkKaQwX8TBNNRfxoOSmn3Xia/cv+sF+GLPZ8vtrLWDif39wj6A+LxEMWHqEOqqsCpY/EqbSjudobDftXUSytqioKPLnz0/evHk9HYqIJGB9qL2Xc861B01jN5KENGNNJGtwq7iaiKQP6/SzdDPnAPzfRsvvEx+0JN4JzOUQn3CAcsygNQspz0zmcSjZywXiS0sqKOkWySaKFSvGu+++a7dt//79zJ4920MRiYjVBa4zhV3OTS9PYzcSKyMwmiC3zhWR9KXEW8SDElcyT1MKPu8QPPWd5ffng+DN1pCoR288Zt7mR9ugr2rlIjmL2WzGbLb/s37jxo2MHj3aQxGJCMAgVtOIz/kfF1M/OB26kRiwzHIDA9PYk+qDdhHJeEq8RTxsCPU4wyhCGchaHkv2OP+U+m4uDIdh6yy/P9cY3mubJOlOjrVauYiIiKS/MCJYyM/OHexkN5KUGIF3actcDjlsYSYinqHEW8RDIjCxnF9Yzi8AtKQCl4hO9vhL3HS8Y8kRGPwtmIGnG1gGaieTbrD8R0Brv0RERDLGj5x17sAUupE4w4iB52nKn4ymAWUc1pDRg3YRz3GpuNr69eu5ePG/KTIHDhwA4Omnn05ybFhYWBpDE8m5pv7bJszKgOXp9Itsde1CK36F/qstSfewevDBwy4l3QDv0FZruEVERDLIaa6lflDCbiRvtrLrRuKM52nKczS2G88TV09XkTURz3Ip8T5w4IAt2U5ozpw5Do83uJgAiOQG0xIl3WDJm8e72q979VF4bBXEm2FwHZjT0dLj00lGDLxLCM/j2uAuIiIiKYvAxHEiWczPzCc85YM//Mm+G8lLwU7fpy4BrOWxJA/QE7cwU1tQEc9zOvEODQ3NyDhEcoUITEmSbiszljffTiXf6/+A3ishzgz9asFnnZxOup+lEd2ophZhIjnUl19+yb59+2yfT5w4AcDDDz/s8HiDwcB3332XKbGJ5AbzOMSTrHOuV/enB+DZ7y2/O+hGkprDXEp2n7WFmdqCimQNTifeLVq49h8CEUnqOJEpDsNOJd0bT0D35RAbD31qwPwu4OVcuYYePMBsHP/xLSI5w4kTJ2zJdkIbN250eLxmp4mknwhMzifd8w7BiJS7kaTGum47uaQ6EF8l3CJZhEtTzUUkbQrjnbYLbD0Fjy6FO3HQvRos7gp5kk+6e/AA42jKbs7RjLI0JDBt9xeRLO306dOeDsEt9957L3/++afdtilTpvDiiy/aPh8+fJhnnnmGsLAwSpYsybPPPsu4ceMyO1SRFB0n0rmke9HPbncjSUjrtkWyDyXeIhnIusarMn5s4iRDWev+xX44A52/hpg46FIFvu6eYtLdj5ospjuAEm6RXKJ8+fKeDsFtkydPZtiwYbbPRYoUsf0eFRVFu3btCAkJYc6cORw5coQnnniCokWL8uSTT3oiXBGbhGO9Uw/Y09CNxHqUGbRuWySbUeItkkESrvFyeu12cn78Ex5ZArfuwsOVYVkP8PZK8ZQphKTljiIimapIkSIEBAQ43PfVV19x584dvvjiC/LmzUv16tUJDw9n+vTpSrzFoxKO9UYM9OCBlE+wdiOJN7vcjcQI7GMopSmiddsi2ZD6eItkgMRrvNKUdO89Bw8vgZux0K4irOoF+VJ+ZtaGChqMRSRbeeeddyhevDh169Zl6tSp3L1717Zv7969BAcHkzdvXtu29u3b8/vvv/PPP/84vF5MTAxRUVF2PyLpKfFYH4+Z5fya/Alp7EYSD0QTSyC+tNQ4L5Lt6I23SAZweo1Xan76Cx76Cm7cgdYVYE1vyJ/6/9tOoU3a7y0ikkn+7//+j3r16uHn58eePXuYMGECFy5cYPr06QBcvHiRChUq2J3j7+9v21esWLEk15wyZQqTJk3K+OAl13JprE9DNxIrrecWyd70xlskA1TGDyNprBR86AK0/xKiYiC4PKztAwVSXzvWgwe0pltEPO7FF1/EYDCk+HPs2DEAxowZQ8uWLalVqxYjRozg/fff54MPPiAmJsbt+0+YMAGTyWT7OXfuXHp9NRHAhbE+Dd1IrLSeWyT70xtvERckLKASiG+SzwBhRPAjZ+lAJb7juHs3+vkitF0M125Ds7Lw3eNQKG+qpz1LI7ULE5EsYezYsQwaNCjFY+677z6H2xs3bszdu3c5c+YMVapUISAggEuX7PsVWz8nty48X7585MuXz/XARZwUiC/9qcVCfk7+oMTdSBY9mmJh1MQ+4WGqUlLruUVyACXeIk5KXEClP7VYzGHb57l04kf+THkAdsYvlyFkMUTegsb3wIa+UDj1pPs92vICzdJ2bxGRdFKyZElKlizp1rnh4eEYjUZKlSoFQFBQEC+99BKxsbF4e1tm/mzZsoUqVao4nGYukhnCiEh5zE/YjaRzFVjSPdXCqAkZgI5UUcItkkM4lXgn90Q6NQaDgZMnT7p1rkhW4qiASsLBNh6z3X63Hf0b2iyCKzehQRnY2A98Un5js5weBFFWA7OIZEt79+5l//79tGrViiJFirB3715Gjx5Nv379bEn1448/zqRJkxgyZAjjx4/nl19+YdasWcyYMcPD0UtuZX0Yn6zE3UiW94C8riXdn9FZY7tIDuJU4h0fH48hUauDO3fucOHCBctF8uShePHiXL161VaFtHTp0nbVR0WyM2cKqKQ56f7jKrReBJejoU4AbOoHRfOneIoBlHSLSLaWL18+li5dyuuvv05MTAwVKlRg9OjRjBkzxnaMr68vmzdv5plnnqF+/fqUKFGCV199Va3ExCMSP4xPwo1uJFb9qUUn7tfYLpIDOfVfgTNnzth9vnbtGiEhIVSuXJm33nqLoKAgjEYj8fHx7Nnz/+3deVxU1fvA8c+AAiKbC664a5ZpbinhgrjiRmpumbnvaa65lWnaouWWWWbumn3V0p+aSynu5r6R5paaiJhoioLigjDn98c0E8MMMDMMDODzfr14xdx77p3nzpDnPveee56DTJgwgbi4OHbs2JERMQuR6fQTqKSWXDuhK/VhkyvR0Gg5RD2EKoUgtBvkz5PmZgq4TLR0zkIIevfubdN2Go2GxYsX2zkay9WoUYPDhw+n2e6VV15h//79mRCREKk7yPWUzwdsrEaiF8ILdKSynSIVQmQlNj3jPXbsWJ48ecKRI0dwdv5v2IyTkxP16tVjx44dVK1albFjxzJ//ny7BSuEo/jhzQJCGMAmEv99pjt5p2su6W5FBbZyKfV74eH3dXe6bzyASr6wozsUdLcoLg1IaREhBADLli0zu1yj0aCU6b9C+uWOTryFyGrMTZyqt5iT9OVn8xvaWI1ECPF8sKmc2MaNG2ndurVR0p1Urly5aN26NRs3bkxXcEJkJX2oQTjD+ZEOKAuGlfeiGnXwowgeKTe6HgMNl0NEDLxQAHZ2h0J5LY5pPPXlbrcQAoCrV68a/Vy5coXWrVtToEABPv74Y/bs2cP58+fZs2cPU6ZMoUCBAoSEhHDpko3VF4TIgRZzklJ8SSOWU4ovWcxJQJeM/8gfKSfdNlYjSUr/+JgQImey6Y53bGwsMTExqbbR180UIifxw5uCRFv0NPdSwlJvcCNWl3SH34dy+WBXdyhiPknXgMl7dqQSn9LYgkiEEM+DUqVKGb2eNm0aR44c4ffff6do0aKG5RUrViQwMJBevXpRvXp11q5dy5gxYzI7XCGyHHMTqfbnZ+7xmLHsSHl4uY3VSJLSoKtOcoloALmoLkQOZNMd75dffpnVq1enOGP5pUuXWL16NZUryzMqIuepQH40aTdLXdRD3fDyK/egjA/s7gHFvVJs3p2qXGcE39KSSQRylL78SKf0RiGEyMEWL15Mp06djJLupIoXL06nTp1YuHBhJkcmRNZkbiJVLTCG0JST7gt3rK5Gkty3tORzmjKWHSZ32oUQOYdNifeECROIiYmhevXqjBgxgnXr1rF//37WrVvH8OHDqVmzJg8ePGDChAn2jtdm33zzDaVLl8bNzQ1/f3+OHj3q6JDE8+p2nG4itT/vQklv2NUDSqR+ZXslpwEYSG0+ohG18MuMSIUQ2VhkZCRubqlXRnBzcyMyMjKTIhIia0vpwnqKo9wu3dX151ZUI0nuC5rSmoqMS3JHXYtiAJuIREaOCpGT2JR4t2nThmXLlqHRaJgzZw6dOnUiKCiITp068dVXX+Hk5MTSpUt5/fXX7R2vTdasWcPIkSOZNGkSJ0+epGrVqgQHB3P79m1HhyayoUsWDjU3684jaLICzt+B4p664eWlfdLcLBHF5X+HnwkhhCX8/PxYv349T548Mbv+0aNHrF+/Hj8/uZAnBOiGd4+ijmWNr0TrHhe7aV01kqQGUpPR1DV7p136fSFyHpsSb4Du3bsTGRnJ8uXLGTFiBL1792bEiBEsX76ciIgIunfvbs8402XWrFn069ePXr16UalSJebPn4+7uztLlixxdGgiG9KXFrNa9GPdxCtnbkNRD93w8nKWz0h+nL+tf08hxHOrb9++/PXXX9StW5eNGzdy9+5dAO7evcuGDRuoV68e4eHh9OvXz8GRCpF1dKJS2j18OqqR6GmADwgEzJ9XOKORqiVC5DAaZa7GSA4SHx+Pu7s7a9eupW3btoblPXr04P79+2ZnXn/69ClPnz41vI6NjaVEiRLExMTg5ZXyc7ji+bGYk4bSYha5/0R3p/vETd2s5Xt7wosFrXpPZzSEM1wmXBEiB4iNjcXb2ztD+xWtVku/fv1YunQpGo3upN7JyQmtVlf8UClFr169WLRokWF9TpYZn7nI3hZz0mhyNbOux0CDZXD1vq4ayd6eKU6Mmpr3qMMw/A19etLzCmc0fEcIfahh03EIITKPNX2LTbOaJ/Xw4UP+/PNP4uLiqF+/fnp3Z3d37twhMTGRwoULGy0vXLgwFy5cMLvN1KlTmTx5cmaEJ7IBc/U8+1CDaB4zhtC0dxD7FJqv1CXdBd11w8utTLrhv2FnkngLISzh5OTE4sWL6d69O8uXL+f06dPExMTg7e1N1apV6datG0FBQY4OU4gsIfmM5mbpq5FcvZ9mNRJzNIA/xTnCDWZwkFkcYsG/CXYfahBMOS4TTXkz9cOFENmfzYl3eHg4w4YNY+vWrWi1WjQaDQkJCQAcOHCAfv36MW/evGzZqY8fP56RI0caXuvveIvnT9Kr3xpgFHXoRCWO87dlSffDeGjxAxy5oXv2a0c3eLmQTbHIsDMhhC0aNGhAgwYNHB2GEA5l7iJ6UuaeszZiZTWSpJzQsJr2lMaH11hseBf9JGrBlMMPb8OPECJnsinxjoiI4LXXXuPu3bu0adOGqKgoDh06ZFjv7+/PnTt3WLVqlcMT74IFC+Ls7MytW7eMlt+6dYsiRYqY3cbV1RVXV+tKQYicJ/nVbwXM4CAzOGjZDuLiodX/4OB13Synod2gqvm/uZTo63frh51JhyyEEEJYJ+lFdCc0hrvMScURn/IObKhGoqcBFhBCRyqzm6spTqIm/bsQOZ9Nk6tNmjSJe/fusXfvXtauXUvTpk2N1ufKlYv69etz4MABuwSZHi4uLtSsWZOdO3calmm1Wnbu3ElAQIADIxNZ3UGup371OzWPnsHrq2HfNV09z+1vQw3ztXRT4oyGI/RlNz0IZ7g86yWEsFpCQgKzZ8+mdu3aeHl5kSvXf9fbw8LCeOedd/jzzz8dGKEQGSv5RfSUSnX9yV3zO7CxGglAAH5EMMLQf8skakI832xKvLdt20a7du2oUyflkgulSpXixo0bNgdmTyNHjmThwoUsX76c8+fPM2jQIOLi4ujVq5ejQxNZ1GJO8iZrbdv4SQK0WwO7roKHC/zaFWoVt3o302hCLfwIooxcCRdCWO3x48c0bNiQ9957j2vXruHl5UXS+VTLlCnD0qVLWbFihQOjFCJjpVWqK5IYdnOVLZi5AJXOaiRzaG7Uf/vhzQJCcP43+ZbRbEI8X2xKvKOjoyldunSqbZRSRjODO1Lnzp2ZMWMGEydOpFq1aoSFhfHrr7+aTLgmBPx3ddyme91PE6D9j7D9Crjnhq1vQYBt8wO8SjGbthNCCIDPPvuMAwcOMHXqVKKioujbt6/Rem9vbxo0aMC2bdscFKEQGS+1u8yLOUkpvqQRy9lFuPGG959As+8hLEpXjWRXD6hQwOL37UFVauFnsrwPNQhnuIxmE+I5ZNMz3oULF+bSpUuptjlz5gwlS5a0KaiMMGTIEIYMGeLoMEQ2kOYEKymJT4ROa2HrJciTC7a8BfVL2RSDDD0TQqTXmjVraNiwIWPGjAEwWzKsbNmynDp1KrNDEyLT6O8y60t1OQEjCOAmD1KexTyd1Ui+pSUDqZ1qTHKXW4jnj013vJs2bcrmzZs5ffq02fX79+9n165dtGzZMl3BCeEI5q6Op+lZInRZBz9fBFdn+LkLBJW2OYZpNJFOWQiRLhEREbz66quptvH09CQmJibVNkJkd/q7zAOpaZgo1Z9F5pNuO1QjaU1F+wQuhMhRbEq8J0yYQJ48eQgMDOTTTz/l8uXLAPzyyy98+OGHNG/enIIFCzJ69Gi7BitEZvDDm2k0sXyDBC10Ww//dx5cnGHDm9CkbJqbaf79MUeGmQsh0svT05Pbt2+n2ubKlSv4+vpmUkRCOM4q/mA+JwypttlxbXaoRvIFTeXCuRDCLJuGmpcuXZpt27bx5ptv8uGHH6LRaFBK0bp1a5RSlCxZkrVr11K0qHWzOAuRVdwmzrKGiVrotRHWnIXcTrCuEzQvb9GmCt1wtHfYanQCIMPMhRD28Nprr7Fp0ybu37+Pj4+Pyfrr16+zdetW2rVrl/nBCZGJIolhLKGpN3qc/mok02nKe9RNR6RCiJzMpsQbdLW6L126xKZNmzhy5AjR0dF4eXnh7+9PmzZtcHFxsWecQmSaSGKYxaG0G2oV9N0EK09DLif4sSO0fsHi93FGQ2sqkptchmfPZIZTIYS9jB49moYNG9K4cWO++uorEhISAHj06BGHDh3i3XffJSEhgZEjRzo4UiEy1iWiU5+55UkCtLW9GokGOEJfs5OpCSGEns2JN+jqdbdr106uloscIZIYLhHNP8SlPbmaVsHAzbAsDJw18L83oO2LqW7Sg6qs5LRJgt2HGgRTjstEU578knQLIewiMDCQr7/+mmHDhhEYGGhY7unpCYCzszPz5s2jZs2ajgpRiEzhQe6UV9qhGsko6kjSLYRIk02Jd6NGjejZsyfdu3dPsc3KlStZsmQJu3btsjk4ITLLYk7Sj58N6baGFJ7/AlAK3t0KC0+Ckwa+bwcdX051/5voQmsq8gmNzCbYMsOpECIjDBo0iKCgIObPn28yOu2dd97h5ZdT/7dLiJzgOH+bX2GHaiTOaBiGvx2iFELkdDYl3nv27CEoKCjVNteuXWPv3r227F6ITHWMSPrys9GyVJPuEdtg3nFddr60DXSpkur+G1DKMMOpJNhCiMwSERGBj48PL730EnPmzDHb5sGDB9y7dy9Llf8Uwp5mcIAx5p7vfpYIb9lWjcQJDVp5PEwIYSWbZjW3RFxcHLlzpzK0R4gsYDEn8WeRZY2VgjGhMOeI7vWi16F71TQ3W8kb6YhQCCFsU6ZMmRQTbr2vvvqKMmXKZFJEQmSu6RxgNKGmF9P11UjWWVeN5D+KH+lAOMPpQw07RiyEyMksvuMdERFh9Pr+/fsmywASExO5fv0669ato3Tp0ukOUIiMEkkM/dmU1tPcOkrBB7tgxr+Trs1vBb2rp7mZlBURQjiKUgqlUv8XLq31QmRXKc5kno5qJHpawJe80r8LIaxiceJdunRpNBpd1WGNRsOcOXNSvZKulGL69Onpj1CIDHKJ6LQnUdObvBem/qb7fW4LGPCqRZvVknrcQogsLDIy0jDZmhA5ySfsM+3hk1YjcdbAmg5pViPJhYaEZHuSsp9CCFtYnHh3797dUK97xYoVVK1alWrVqpm0c3Z2Jn/+/DRq1IjmzZvbM1Yh7KoC+VOfRE3v0326xBtgVjMYUtui/TtJxyyEyGRTpkwxer1nzx6z7fSj01avXs1rr72WCZEJkXkmsJPvOGG8MHk1klXtod1Lqe7HlzycZCDbuCJlP4UQ6aZRNowzK1OmDCNGjGDo0KEZEVOWExsbi7e3NzExMXh5eTk6HGElfZmwCslmEo8khpLMTj3x/uIAjN2h+/3zJjCmrsXvO52mvIfl7YUQz4+M6lecnP6bukV/sTw1xYoVY/369dSqVctuMWRV0pfnXMeIZD8R1KckG7nIp+w3bqAUDNmqmxhVX43krdQnRtXTAAt5Xcp+CiHMsqZvsWlW86tXr9oUmBCZIWmivY0r9GcTWhROaFhAiGEilEtEp550zz70X9L9cUOrku4vJOkWQjjA7t27Ad3jXvrSnz169DBppx+d9uKLLxol60JkNz1Zz3J+T7mBuWokFibdoBsVN4BNhDOcIGQiQiGE7WxKvM+dO8eOHTvo0qULvr6+Jutv377N6tWradq0KS+9lPowHiHsaTEnDYm25t9l+uRai2IAm3iFQjzkGR6kMuv+10dh5Hbd7xMDYUKgxTH8SAc6Utmm+IUQIj0aNGhg+H3SpEkEBQUZLRMiJzlGZNpJtw3VSJJLRHGZaLnTLYRIF5sS72nTprFz506GDBlidn2BAgWYPn06p06dYunSpekKUAhL6Wcp10+YZu5udiIKfxalfqf7u+Pw7i+638fXg4+CLI7BGQ0BlLC4vRBCZJRJkyY5OgQhMtR+TKvrGNhYjcQcmUxNCGEPNo0v279/P40bN05xeJqzszONGzdm37596QpOCGtYOkt5qi2WnIKBW3S/jwqATxuBRpPaFgYy4YoQIis5ePAgI0eOJCoqyuz6mzdvMnLkSA4fPpzJkQlhH/UpmfJKG6uRLKUN71HHcIIsfbsQwl5suuMdFRVFiRKp39UrXrw4N2/etCkoIWxRgfw4oTFKvpMPN0/Vit+h78+634f5w/SmaSbd71GHTlQijmcy4YoQIkuZOXMmp0+fZtasWWbXFy1alM2bN3Pjxg3WrFmTydEJkX5F8cSf4hzhhvEKG6uR9KAqPdHdFR+Gv0ymJoSwK5sS77x583L79u1U29y+fRs3NzebghLCFn54s4AQo5IfU2nCWELT3njVGei1UZehD3oVZgenmXR/S0sGYllnLoQQme3YsWM0btw41TaBgYGEhlrwb6QQDpa8QknSOV2MfHEAJugmGeTzJjAiIM19B1KCGQRTCz/DMj+8JeEWQtiVTYl3jRo12LBhA9OnT8fHx8dk/b1791i/fj01atRIb3xCWKUPNYxKfqQ5cznAT2eh23pdjc++1eHrlmkm3RqgNRXtFbYQQtjd7du3KV68eKptihQpkuaFdCEcLWmS7YSGaTRhHDtMk24bq5F0oYpR0i2EEBnBpme8Bw8ezN27d2nYsKHJc9x79+6lYcOG3Lt3L8XJ14TISH54E0QZ/PBOfeZygA0X4K3/g0QFPavBdyFonNJ+pnsUdeRKuBAiS/Px8SEiIpXJp4Br167h4eGRSREJYb3kE6dqUYwj1DTp/sb2aiRyIV0IkRlsSrzbtGnDiBEj+P3332nYsCHu7u6ULVsWd3d3GjVqxOnTp3nvvfdo27atncMVwjo/ci7llZv/hE4/QYIWulaBRSFgQdLthO7ZLyGEyMpee+011q9fz/Xr182uj4iIYMOGDdSpUyeTIxPCcuYmTtUmb7TgBAyxrRrJIl6XC+lCiExhU+INuklbfv75Z4KDg8mbNy+RkZF4eHjQokULtmzZwueff27POIWwyDEimcVBjhFJJDHM4KD5hr9ehvY/wjMtdH4ZlrUFZ93/DmkNTR8pd7uFENnAyJEjefToEXXr1mXFihWGCU9v3rzJ8uXLqVu3Lo8fP2bUqFEOjlSIlFUgP6leEl9yCgZs1v1uZTWSTXShD/JYpBAic9j0jLde69atad26tb1iEcJiSSdZAd0V8W85xk9J7nD74Wl+4x1/QdvVEJ8I7V+C79tBLsuuQcndbiFEdhEYGMisWbMYNWoUvXr1AkCj0aCU7vKik5MTc+bMITDQ8iG5QmQp31tfjUSvB1VliLkQIlOlK/EWwhGSTrKiIeU71JE8MF24JxxeXwVPE+H1ivC/9pDb2ahJSvuUWp5CiOxm2LBhNGzYkPnz53Ps2DFiYmLw8fGhdu3aDBw4kMqVKzs6RCFSleIkqavOQE/rqpEAtKUi71NfJlMTQmQ6SbxFtpJ8khWL6nPr/RYBrf8HjxOgZQX4sQO4OJs0609NvuOEyfJVtKcjcpIqhMheXnnlFebNm+foMISwidlJUm2oRqInSbcQwlEsGl/r5ORErly5+PPPPw2vnZ2d0/zJlUvyemFf5iZZscih69DiB4h7Bk3LwrpO4Gr69zmAmkwgEKdkT5Q5oyGAEraGLYQQQggrLeYk/iwyXmimGoklE6OCbni5JN1CCEexKDMODAxEo9Hg7u5u9FqIzHaCv63f6NgNaP4DPIyHhqVhw5vgZv5PvyDu+OHNAkIYwCYSUTLEXAiRLfTu3RuNRsNnn31G4cKF6d27t0XbaTQaFi9enMHRCWG5SGI4yHX68bPxpXYbq5HUwY8vaW6SdOvni/EgNw95RgXyS18vhMgwGqWfZUWkKDY2Fm9vb2JiYvDy8nJ0OM+tSGIoxZfW3fE+eRMar4D7TyCwFGx9C/K6pLrJFzRlNHWJJIbLRFNeOmIhhJ1lRL/i5OSERqPh/PnzvPDCCzg5WTZppEajITEx0S4xZGXSl2d9kcTwCftYwAnTnv7Xy9Dm34lRO78MK9+weGLUo/Q1SbqTzhej54SGBYTITOdCCItZ07fIWHCRbRzkunVJ9+lb0PR7XdJdpwRs7pJm0g0wjlC6UBk/vCXhFkJkG1evXgWgePHiRq+FyA4Wc5K+/Gx+ZdJqJG9YV40EII5nRq+Tzxejp0UxgE0EU076fyGE3UniLbIF/ZVpi529rbvTHf0YaheHX7qCp6tFm2qBy0RLpyuEyFZKlSqV6mshsqpIYlJOupNWIwl5AVaZViNJjTMayv9belQvtfliElFyDiCEyBAWJd6WPieWnDw3JiyVtC530s5O/5yXuSvTKbpwR5d033kENYvCtrfBy7KkG8x30kIIIYTIGAe5bn5F8mokP3U0W40kJSnN0VKB/DihMXteIecAQoiMYlHivWzZMrPLNRoN5h4R1y+XxFtYIulzVkmfr5rOAcYSat0c5pfuQqPlcCsOqhaG7d3Ax83izWUiNSGEECJz7cLMYxEWViMB0ABH6Es49wEojQ9xPEtxjpbkk6jqyTmAECIjWZR4J39OTKvVMmzYMA4fPsywYcOoX78+hQsX5tatW+zbt4+vvvqKgIAAZs+enSFBi5wj+XNW+uerrnKPT9lv3c7+ugeNVsDNh1C5EOzoDvnzWLSpMxpW0Z4ASkiHK4TIlmR0msiOIonhO04YL7SiGgnAYGpTCz+rSoX1oQbBlOMy0eQld6qJuhBC2INFiXfy58SmTZvGkSNH+P333ylatKhhecWKFQkMDKRXr15Ur16dtWvXMmbMGPtGLHKUORwxGeqViLI46e7AS6zlPITfh4bLITIWXioIO7tDQXeL40hE4Ute6XCFENmWjE4T2dEloo0XnLwJzVZC7FNdNZJNXcA9d6r7KEc+m95bJlEVQmQmy6eETGLx4sV06tTJKOlOqnjx4nTq1ImFCxemKziRs0USw0wOmiy3pkJ8cyrwzfV6uuHlETHwQgFd0l0or1WxyDNdQojs7urVq0Y/V65coXXr1hQoUICPP/6YPXv2cP78efbs2cOUKVMoUKAAISEhXLp0ydGhi+dIJDHs5iqRxAC6560NbKxGUpcSGRWuEELYjU2zmkdGRuLmlvpzs25ubkRGRtoUlHg+XCLa7PPbL1KQ89yxaB/9bqwkb6NVcPU+lMsHu7pDUc8U2zsB02hKfvIYnu2SZ7qEEDmBjE4TWV3yOV2m0YRXKca71Gbu2c02VSPpQVWrhpgLIYSjaJS58WdpqFChAkop/vjjD7MJ+KNHj6hSpQpOTk454kq6NYXRheUiiaEUX1pXmzupqIcQtAwu3oXSPrC3J5RMOXn+kQ5Gz3BHEsNlouWZLiFEpsuMfqVChQo0b96cuXPnpthmyJAhbNu2LUf01WmRvtyxUu3zL9zR9ee34nTVSHZ0T3Vi1CHUphz5qEsJSbqFEA5lTd9i01Dzvn378tdff1G3bl02btzI3bt3Abh79y4bNmygXr16hIeH069fP1t2L54T+llFnf8dXO5szSDz23G6K+MX70IJL9jdI9WkWwMmE6f54U0QZSTpFkLkSDI6TWQlKdbOtrIayQfUZy4tGU6AJN1CiGzFpjveWq2Wfv36sXTpUjQaXbLk5OSEVqsFQClFr169WLRokWF9diZXye1DX6vbg9xc/bfkR51/n8u6TDS3iaMza9Pe0Z1Huk76zG0o7qm7010u7eezd9ODIMqk4wiEEMI+MuuO9/M0Oi0t0pc7ltk73n/dgwbLdBOjVi6ku4ieysSoX9CU0dTN+GCFEMJC1vQtNj3j7eTkxOLFi+nevTvLly/n9OnTxMTE4O3tTdWqVenWrRtBQUG27FrkUEmf60pKAyzkdYIpx3n+SXtH0Y91E6+cuQ1FPGBXD4uSbieQydOEEM+Vvn37Mn78eOrWrcvEiROpV68eBQoU4O7du+zfv58pU6YQHh7O1KlTHR2qyKH0F9wr/PtIl1Ht7Gv3rapGcpS+codbCJGt2ZR46zVo0IAGDRrYKxaRQyWv1Z2UAvrys2U7uv8EgldCWJRu1vJd3XWzmFtgJHVkSLkQ4rkyevRo/vzzT5YuXcobb7wBmB+dNnr06AyN49NPP2XLli2EhYXh4uLC/fv3TdpEREQwaNAgdu/ejYeHBz169GDq1KnkyvXfacqePXsYOXIkZ8+epUSJEkyYMIGePXtmaOzCdsknUltACH2owT0eM/r6Wl3SbUE1EidgAa9L0i2EyPZsesY7q/j000+pU6cO7u7u+Pj4mG0TERFBq1atcHd3p1ChQowePZqEhITMDfQ5d5Drtk+gphf7FJqvhON/666I7+wOL/maNHPCtByZMxqG4Z++9xdCiGxGPzpt9+7d9OjRg+rVq1O6dGmqV69Oz5492bVrF4sXL87wR8Li4+Pp2LEjgwYNMrs+MTGRVq1aER8fz8GDB1m+fDnLli1j4sSJhjZXr16lVatWNGzYkLCwMIYPH07fvn3Ztm1bhsYubJP8grsWxQA2sZmLjL6xDhqtSLMayQfUZzc9uMYI+lAjk49ACCHsz+Y73gkJCcydO5dVq1Zx4cIFHj16ZEhow8LCWLBgAcOHD+eFF16wW7DJ6TvzgIAAFi9ebLJe35kXKVKEgwcPcvPmTbp3707u3Ln57LPPMiwu8R/9Fe90eRgPLX+AIzcgnxvs6KZ7FiwZDbqr4oCUChNCiH85enTa5MmTAVi2bJnZ9du3b+fcuXPs2LGDwoULU61aNT7++GPGjh3LRx99hIuLC/Pnz6dMmTLMnDkTgJdeeonffvuN2bNnExwcnFmHIixkbiK1RBQhUQt1E6NejtZVI9nVA4qbPhMpz3ILIXIim+54P378mIYNG/Lee+9x7do1vLy8SDpHW5kyZVi6dCkrVqywW6DmTJ48mREjRlClShWz6/Wd+cqVK6lWrRotWrTg448/5ptvviE+Pj5DYxOpDzG3WFw8tP4fHLgO3q4Q2g2qFjHbVAH7uUYfahDOcHbTg3CGy5VyIYTIwg4dOkSVKlUoXLiwYVlwcDCxsbGcPXvW0KZJkyZG2wUHB3Po0KEU9/v06VNiY2ONfkTmqEB+nJKPP7OwGkkIFSTpFkLkSDYl3p999hkHDhxg6tSpREVF0bdvX6P13t7eNGjQwOFDwCzpzM2Rzto+UiwdYqnHz+D11bD3Gni56kqM1CyW6ibL+Z1jREqpMCGEQDc6bfbs2dSuXRsvLy+jZ6bDwsJ45513+PPPPx0YIURFRRn104DhdVRUVKptYmNjefz4sdn9Tp06FW9vb8NPiRIlMiB6YU7ycqHceQRNVsC5f3TVSHb30N3xNmMLl4kkJvOCFUKITGJT4r1mzRoaNmzImDFj0Gg0Zp8PK1u2LBEREekOMD0s6czNkc46fSKJYTdXiSPemsrcxp4kQNs1sOsqeLjAL12hdnGLNj3AdVvfVQghcoyMHJ02btw4Q/+f0s+FCxfseThWGz9+PDExMYaf69elb8hMfajBIfpYXY1Ei+Iy0ZkYqRBCZA6bEu+IiAheffXVVNt4enoSE2P9Fcus0JlLZ21Kn0yndRV6MScpxZc0YjkhrLLtfvfTBOjwI2y/Au65YetbUMfyix91kQslQgiRkaPTRo0axfnz51P9KVu2rEX7KlKkCLdu3TJapn9dpEiRVNt4eXmRJ08es/t1dXXFy8vL6EdkrhX3j1pdjcQZjZT/FELkSDZNrubp6cnt27dTbXPlyhV8fU1nnU7LqFGj0iwPYk1nfvToUaNlyTtzc1xdXXF1dbXoPZ4HKZUESc4uz3Q/S4TOa2HLJciTCzZ3gfqlLN68B1Wl5IgQQmA8Og1IcXTaqVOnrN63r6+vTX28OQEBAXz66afcvn2bQoV0E2eGhobi5eVFpUqVDG22bt1qtF1oaCgBAQF2iUHYR9K63Q9iY/m6+dA0q5H0oCorOS0TogohcjybEu/XXnuNTZs2cf/+fbNlvK5fv87WrVtp166d1fvO7M5cpC6lkiDBlDPpGNP9THeCFrqsg40XwdUZNr4JDcukusl0mtKAUhzgOnUpIUm3EEL8KyIiIs1+2NbRadbGER0dTUREBImJiYSFhQFQvnx5PDw8aNasGZUqVaJbt2588cUXREVFMWHCBAYPHmy4CD5w4EC+/vprxowZQ+/evdm1axc//vgjW7ZsydDYheWSXqTXPIynWMufLapG8gmN+IRGXCaa8uSXpFsIkWPZNNR89OjR3Lt3j8aNG3PgwAFDGbFHjx6xc+dOgoODSUhIYOTIkXYNNrmIiAjCwsKMOvOwsDAePnwIYNSZ//7772zbts2kMxepS6kkiLnnr8zOYmqpBC10Ww/rzoOLM6zvDE3Lpdhcg67cyHvUpRZ+DCdAkm4hhEgiI0enWWPixIlUr16dSZMm8fDhQ6pXr0716tU5fvw4AM7OzmzevBlnZ2cCAgJ4++236d69O1OmTDHso0yZMmzZsoXQ0FCqVq3KzJkzWbRokZQSyyKMLtLHxaNa/48bB85aVI3kENdlQlQhxHPBpjvegYGBfP311wwbNozAwEDDck9PT0DXic6bN4+aNWvaJ8oUTJw4keXLlxteV69eHYDdu3cTFBRk6MwHDRpEQEAAefPmpUePHkaduUidPplOmnyn9PyVfhbTvvxs3ZskaqHXRlj9B+R2grUdoUUFs001wCjqMAx/6aCFECIVGTk6zRrLli1LsYa3XqlSpUyGkicXFBRk07B4kfEMF+ltqEbSmbXEEi+lP4UQOZ5NiTfAoEGDCAoKYv78+Rw5coTo6Gi8vLzw9/fnnXfe4eWXX7ZnnGbZqzMXKdMn0wPYRCIKJ2AqTVJMeu9hvqxLirQK+m2ClafBWQNrOkBIRbNNG1CKlbwhCbcQQlhg9OjRNGzYkMaNG/PVV18ZjU47dOgQ7777bqaMThM5XwXyo3mSgDJTjUQDaJJdwE9KQYqPsAkhRE5iU+K9b98+vLy8qFatGnPmzLF3TCKL6UMN7vGYsexAi2IcO8hPHsPV6WNEsp8IXqAAY9lh+Y61CgZthqVh4KSB/7WHdi+ZbTqE2sylpR2ORgghng9ZZXSayPl8n7pRpMMv3DRTjUQBa2iPL3nJS242c4kp7DXaXv8ImyTeQoiczKbEu2HDhgwYMIB58+bZOx6RBUQSw8F/a2HX+bc0lz7pBuMJ1kbwK2s5b/2bKAVDf4EFJ3Xjx79vB51MR0k4oeFzmvAedW0+HiGEeF5lhdFpImfSz2Be+pknIZ3f4OaWk+BmWo3EGQ0BlDAk1UXx5BP2WfQImxBC5CQ2Jd6FChXCzc3N3rGILGAxJ+nHz4buUP9MtbkJ1nqxgR1ctf5NlIKR2+CbY7o3WNoG3qpieL81dKA0PsTxTGY4FUKIdHrppZdkdJqwK8MM5gmJ8NY62HhOV43kZ+NqJBowKQ+W/BE2KSEmhHhe2JR4N23alD179qCUMlsXVGRPkcQYJd2gGyI2i0No/v09KZuT7rE74MsjutcLQ6BHNaP38yWvzFAuhBDp5OzszJtvvskPP/zg6FBEDmKYwTwhUVeNZO25FKuRaIBgTCuU9KEGwZSTEmJCiOeKTeXEpk2bxt27d+nfvz/R0aZlpUT2dIlos1OfaFG04oX0v4FSMGEXTD+oe/1tK+hjOotpXnKn/72EEOI55+XlRYkSJRwdhshhLhGNNjERev9bjSRXytVItGC2/CggJcSEEM8dm+54v/322/j4+LBkyRJWrlxJmTJlKFy4sMndb41Gw86dO+0SqMh4Fchv9s42wGb+TP8bTNkLn/2m+/2r5jDwVbPN4niW/vcSQojnXO3atfn9998dHYbIYdy1zrpqJN+nXY1Ent0WQoj/2JR479mzx/D706dPuXDhAhcuXDBpJ8PQsxc/vFnI6ybDze3is/3w0b+zmM5sBu/6m20mnbQQQtjHRx99RFBQECtWrKB79+6ODkfkAAu1x+k/aKBxNZI3zFcjkWe3hRDCmE2Jt1artXccIovQP3d1iOts4zKLCUv/TqcfgA926X6f1hhGBhhWNaE0uwhHi3TSQghhT6GhoQQFBdGrVy/mzp1LrVq1Uhyd9uGHHzooSpEV6Wcsr5Dk+evr6j79h74DC06kWY1kNe2NZjIXQggBGqWU3W9u5jSxsbF4e3sTExODl5eXo8PJFIs5SV9+Tv+OvjwMI7bpfp8SBB82MKxyQsM1hgPIBCtCiOdKZvQrTk6WTeOi0WhITEzMkBiykuexL7eFYcZyFE5oWEAIvVV1Oo7sw7ovl/5XjSTJxKh6+vZ9MJ2/RQghciJr+har7ngfOnSIDz74gGPHjqHRaPD39+eTTz7B39/8sGGRPelnLE23b47+l3R/GGiUdAMsSHJ3WxJuIYSwr927dzs6BJHNGGYs//eBMy2K/upnjo9drku6waQaCehy8QHU5AMCpT8XQogUWJx4nzlzhsaNG/PkyRPDsp07d3Lw4EGOHj3Kyy+bDjcS2UPyIWWXiDap2221BSdgyC+638fVhclBRqudMF9iRAghhH00aNAg7UZC/CuSGH7krHH/rxTaCbuYP103Merb345nVR9XEpOdIyhgISf5gMBMjFgIIbIXi8uJTZs2jSdPnvDBBx8QFRVFVFQUH374IY8fP+bzzz/PyBhFBlrMSUrxJY1YTim+ZDEnqUB+nEjHxHhLT8GAzbrfR74GnzWGZM8UplZiRAghhO0OHTpEo0aN8PT0xMvLi6ZNm3L06FFHhyWyMP25wCi2G69IUo3kq6++4vuBn3GIPmb3kYiSfl0IIVJh8TPeJUuWpHTp0uzbt89oeYMGDQgPD+fatWsZEmBWkJOeC0t6dxugFF8aXd12RkM4w9nGFdue8f7+d+ixQXf5e2ht+LK5SdKd9H1kSJoQ4nmUUf3KmTNn8Pf3NxqdBpAnT57nfnRaTurL7SmSGJNzAUBXjeTfiVFnzpzJyJEjAdjNVRqx3GQ/+nlbpF8XQjxPrOlbLL7jfevWLV577TWT5f7+/ty6dcv6KEWmS353ew5HTDraRBSbucgF7lj/Bqv/gJ4bdUn3oFdTTLoBRhAgnbMQQtiZjE4T1jL7eFmSaiTTpk0zJN1AiqPiPqeJ9OtCCJEKi5/xfvbsGR4eHibL8+bNy7Nnz+walLA/cxOmzOIgGjB5mnsQW61/g7Xn4O3/A62CvtXh65YpJt0aYBgyIZ8QQtjb/v37qVevHh9//LFh2eTJk9mzZw979+51YGQiq9In0obk+8vDMGYHAKOmvE/tsZ2IJMZoMtQFhDCATSSicAKm0ZT3qOugIxBCiOzB4jveInszd0Vbi2nSbZONF6DLOkhU0KMqfBcCTikn3Qt5Xa6KCyFEBpDRacJa+kTaGY1RNZLWH/Zl9ocuRnPA6PWhBuEMZzc9uMYIRkvSLYQQabKqnNjKlSs5fPiw0bLLly8D0LJlS5P2Go2GLVu2pCM8YS8mV7TtZcuf0PEnSNDCW1Vg8esmSbcGmEdLCuBOACUk6RZCiAwio9OELfpQgzsL9jPu32okg8eNYN5kL1SSUXID2EQw5YzufEt/LoQQlrMq8b58+bIh0U7u119/NVmmSWGosch8fnjzOU0YTaj9drrtMrzxIzzTQqeXYXlbcDYdRPEFTRlIbfu9rxBCCCHsZunSpYwbMByAfiMH88ZnQ/hGs8KojX7Wckm2hRDCNhYn3levXs3IOEQmuEWc/Xa28y9ouwbiE6Hdi7CyHeQy/+TCqxSz3/sKIYRIlYxOE9ZYuXIlffr8WyLs3dosmlGQCpqbJqPknNFQ/t+KKEIIIaxnceJdqlSpjIxDZIDkpcNmccg+O94bDiGr4EkChLwAqztAbmezTaWjFkKIzCWj04SlVq9eTY8ePVBKwcCaMKc5SgPj2cHnNGEcO0hE4YyG7wiRu91CCJEOVg01F9nHYk4aZjF3QsNIAuzzfPdvEdDqf/A4AVqUh586gkvKSbd01EIIkXlkdJqw1Nq1a3n77bfRarW6aiTftDJUI0lE8SrFCGc4l4mmPPmlLxdCiHSSxDsHMlc6bLY97nYfjoSWP0DcM2haFv6vM7ia/xNyAg7Rh1r4pf99hRBCWERGpwlLbNy4kS5dupCYmEiHHl1Y910FVJKJUfWj1WQCNSGEsB9JvHOAY0SynwheoAB5ceEf4kzubiem92738b8heCU8iIeGpWHDm+CW8p+PFohDZtAVQgghspItW7bQsWNHEhISeOutt1ixeAXLnH431OWW0WpCCJExJPHO5nqynuX8brTMCQ0ajGt0O6FLhm1y6iY0/R5in0L9krCpC7jnTnUTebZbCCGEyFq2bdvGG2+8wbNnz+jUqRPLly/H2dmZPtQgmHIyrFwIITKQJN7ZTNIJ027ywCTpBgzPdWtQaNElwcGUYyvmJ9tJ1elb0OR7uP8EAvxgy1uQ1yXVTeRquRBCCJG17Ny5k7Zt2xIfH0+7du1YuXIluXL9dxoow8qFECJjSeKdjSSfMK0DlVJsq0XxIx0AuMRdPmC39W947h9osgKiH0Pt4vBLV/B0NdvUGQ3TaMKrFJOr5UIIIUQWsnfvXkJCQnjy5AkhISGsXr2a3LlTH7kmhBDCviTxzibMTZi2lrOpbrOfCOZy1LY3vHAHGi2Hfx5BjaKw7W3wdjPbtBMvM5NmkmwLIYQQWcxvv/1Gq1atePz4MS1atOCnn37CxSX1kWtCCCHsz8nRAQjLXCLaZMI0LRBMuRS3sTnpvnRXl3TfioOqhSG0G/iYT7oB1nHOtvcRQgghRIY5fPgwLVu2JC4ujqZNm/J///d/uLqaH7kmhBAiY0ninU1UID9OaIyWOaNhEa+ziS7J1qTDX/eg0Qq4+RBe9tUl3fnzpLpJIorLRNsrAiGEEEKk0/HjxwkODubBgwc0bNiQbzYs55DbTSKJcXRoQgjxXJLEO5vww5sFhOD8b4rtjIYRBADQmoos5PX0J9/X7kPD5RAZCy8WhJ3dwTdvmpvJDOZCCCFE1nHq1CmaNm1KbGws9evXp8Omj3nRfQGNWE4pvmQxJx0dohBCPHck8c5G+lCDcIbzHnXQopjBQUoym+kc4BUKpa9Sd2SsLumOiIEK+WFXdyjsYdREA/xIB76gqdEFAJnBXAghhMgaTp8+TZMmTbh//z4BAQEs2PI/3s27w2iOmAFskjvfQgiRyWRytWxoFocMSbYCxhBKY0rbvsO/H+iS7qv3oWw+2NUDinoaNdEAC3mdjlQGoAuVpd6nEEIIkYWcO3eOJk2aEB0dTe3atfnll1846Wk6R4z+ETFL+++kpUylzxdCCNtI4p3NmJtkDWAn4bbtMOqhbiK1y9FQ2gd29wA/L0CXbA+gJo0oQwAljDpbqfcphBBCZB0XLlygUaNG/PPPP1SpUZUPfv2OB97/zRGT9NzBmkfEkpcyXUAIfaiRUYchhBA5lgw1z0YiieEf4uy3w3/ioPEKuHgXSnjphpeX/C+ZrksJviWEjlSWJFsIIYTIoi5dukSjRo24desWJaq+wB/bg2mTbwOl+JJtXDGZI8bSR8TMlTKVYepCCGEbueOdTSS94mwXdx9Bk+/h3D9QzFM3vLxMPqMmv3GdGRzgPera5z2FEEIIYVd//fUXjRo14ubNm7zw8ktcCm2NKqCrRqJPlMMZTjjDrX5EzNwoO2uHqQshhNCRO97ZQPIrzul27zE0/R5O34IiHro73eXNDzkbyw65si2EEEJkQdeuXaNRo0ZERkby4osv8tnOZShfd6M2SRPlIMpYlTCnVMpUKpkIIYT1JPHOBlJ6rtsmMU8geCWcigJfd13JsIoFU2yulRrdQgghRJYTGRlJo0aNuHbtGhUqVGDXrl34F65o10TZXClTqWQihBC2kaHm2UAF8qOB9KfesU+h+Q9w7G8okEc3vLySb6qbyJVtIYQQImv5+++/adiwIX/99Rdly5Zl165dFC1aFIAFhDCATSSi7JIo96EGwZSTSiZCCJFOknhnA354M4o6zOCg7Tt5GA+t/geHIyGfG+zoDpULGTVJntw7yZVtIYQQIku5desWjRo14vLly5QuXZrdu3fj5+dnWJ8RibJUMhFCiPSTxDub6EQlZnLQtrvej55ByCr4LQK8XSG0G1QrggY4Ql/CuQ9AACUAOMR1w2vpaIUQQois4Z9//qFRo0ZcvHiREiVKsGvXLkqWLGnSThJlIYTIeiTxzuIiiWEOR2xPuh8/g9dXwZ5w8HSBbW9DzWKA7u72aW6b1OPsKJ21EEIIkaXcvXuXJk2acO7cOYoVK8auXbsoU6aMo8MSQghhoWw7uVp4eDh9+vShTJky5MmTh3LlyjFp0iTi4+ON2p0+fZr69evj5uZGiRIl+OKLLxwUsfUWc5KSzGaGrUn3kwRotwZ2XoW8ueHXt8Hfz6iJ1OMUQgghsrZ79+7RtGlTTp8+TZEiRdi1axfly5d3dFhCCCGskG3veF+4cAGtVst3331H+fLl+eOPP+jXrx9xcXHMmDEDgNjYWJo1a0aTJk2YP38+Z86coXfv3vj4+NC/f38HH0HqjhFJP362fUK1+ETo8CNsuwLuuWFrV6hTwqSZ1OMUQgghsq6YmBiCg4M5deoUvr6+7Ny5k4oVKzo6LCGEEFbKtol38+bNad68ueF12bJluXjxIt9++60h8f7hhx+Ij49nyZIluLi48PLLLxMWFsasWbOydOK9mJP0Z5PtSfezROi8FrZcArdcsKkLBJYy21RmLRdCCCGyptjYWJo3b86xY8coUKAAu3btolKlSo4OSwghhA2y7VBzc2JiYsif/78k8tChQwQGBuLi4mJYFhwczMWLF7l3716K+3n69CmxsbFGP5klkhj6s8n2ut0JWnjr/2DDBXB1ho1vQqMyyap66jiBzFouhBBCZEEPHz6kVatWHD58mHz58rFjxw4qV67s6LCEEELYKMck3pcvX2bu3LkMGDDAsCwqKorChQsbtdO/joqKSnFfU6dOxdvb2/BTooTpEO2Mcolo25PuRC10Xw9rz4GLM/xfZ2hWDg3wBU1x/jf9dkbDe9ThGiNMJlYTQgghhGM9evSIkJAQfvvtN7y9vQkNDaVatWqODksIIUQ6ZLnEe9y4cWg0mlR/Lly4YLTNjRs3aN68OR07dqRfv37pjmH8+PHExMQYfq5fv57ufaYmkhh2c5VIYrj2b2kvqyVqoddGWPUH5HKCnzpCywo4AQt5nfeoSzjD2U0PwhnOdJrJnW4hhBAii3n8+DGvv/46e/bswdPTk23btlGzZk1HhyWEECKdstwz3qNGjaJnz56ptilbtqzh97///puGDRtSp04dFixYYNSuSJEi3Lp1y2iZ/nWRIkVS3L+rqyuurq5WRm4b/fPcWhQasO1et1ZB/03w/Wlw1sDq9vB6RT6jId2oZkiwpa6nEEIIkXU9efKEdu3asXPnTvLmzcsvv/yCv7+/o8MSQghhB1ku8fb19cXX19eitjdu3KBhw4bUrFmTpUuX4uRkfAM/ICCADz74gGfPnpE7d24AQkNDqVixIvny5bN77NZK/jy3TUm3UvDOFlgSBk4a+OENaF+JOvgxngb2DFcIIYQQGSQ+Pp4OHTqwbds23N3d2bp1K3Xr1nV0WEIIIewkyw01t9SNGzcICgqiZMmSzJgxg3/++YeoqCijZ7ffeustXFxc6NOnD2fPnmXNmjXMmTOHkSNHOjDy/6TreW7QJd3v/gLfnQANsKItL3QOZBNdOEBfu8UphBBCiIzz7NkzOnfuzJYtW3Bzc2PTpk0EBgY6OiwhhBB2lOXueFsqNDSUy5cvc/nyZfz8/IzWKaVLZr29vdm+fTuDBw+mZs2aFCxYkIkTJ2aZUmIVyI8TmjSTb7ND0JWCkdvgm2O6BkvaQNdXuMw9bhGXQRELIYQQwp4SEhJ466232LBhA66urmzcuJFGjRo5OiwhhBB2plH6LFWkKDY2Fm9vb2JiYvDy8rLrvqdzgDGEWreRUjBuB3xxUPd6YQj0/W92cmc0hDNcnucWQogsKiP7FWFeVvzMExMT6datG6tWrcLFxYX169fTsmVLR4clhBDCQtb0Ldl2qHlO8SrFrN9o4u7/ku55LY2SboBEFJeJtkN0QgghhMgIiYmJ9OrVi1WrVpErVy5++uknSbqFECIHk8TbwTzIbd0GU/bCJ/t1v89pDoNqmTRxRkN58tshOiGEEELYm1arpX///nz//fc4OzuzevVqXn/9dUeHJYQQIgNJ4u0g+trdV62p2z11P0zao/t9RlMYalpixBkN3xEiw8yFEEJkCZ9++il16tTB3d0dHx8fs200Go3Jz+rVq43a7Nmzhxo1auDq6kr58uVZtmxZxgefAZRSvPPOOyxZsgQnJyd++OEH2rdv7+iwhBBCZLBsO7ladpa8drdFZhyE93fpfp/aGEbVAXTzqo2iDp2oRBzPKE9+SbqFEEJkGfHx8XTs2JGAgAAWL16cYrulS5fSvHlzw+ukSfrVq1dp1aoVAwcO5IcffmDnzp307duXokWLEhwcnJHh25VSiqFDh/Ldd9+h0WhYsWIFnTt3dnRYQgghMoEk3pnM0trdRjOZzzkMo/+dgG1yEIyrB8AAajKBQEm0hRBCZFmTJ08GSPMOtY+PD0WKFDG7bv78+ZQpU4aZM2cC8NJLL/Hbb78xe/bsbJN4K6UYNWoUX3/9NRqNhiVLltC1a1dHhyWEECKTyFDzTJZS7W4n4Fta8iMduM4ImlFOt2LeMRi+Tff7hPowsQFOaDhKX+bLkHIhhBA5xODBgylYsCC1a9dmyZIlJC26cujQIZo0aWLUPjg4mEOHDqW4v6dPnxIbG2v04yhKKcaNG8fs2bMBWLBgAT179nRYPEIIITKf3PHORJHE8A9xZutya4EX8SWIMkQSwzauwMITMHirrsHYujClIU7AAkKohR9CCCFETjBlyhQaNWqEu7s727dv55133uHhw4cMHToUgKioKAoXLmy0TeHChYmNjeXx48fkyZPHZJ9Tp0413G13tIkTJ/LFF18AMG/ePPr27evgiIQQQmQ2SbwzSVrPdSedifwg12FZGAzYrFs54jWY2pgQTUXm0UrucgshhHCocePG8fnnn6fa5vz587z44osW7e/DDz80/F69enXi4uKYPn26IfG2xfjx4xk5cqThdWxsLCVKlLB5f7aaMmUKn3zyCQBz5sxh0KBBmR6DEEIIx5PEOxOYe65bn3wrTGci379yE/TeqFs5pBbMbAYaDd14RZJuIYQQDjdq1Kg0h0qXLVvW5v37+/vz8ccf8/TpU1xdXSlSpAi3bt0yanPr1i28vLzM3u0GcHV1xdXV1eYY7GHq1KlMmjQJgBkzZqTrQoIQQojsTRLvTGDuuW4F/EgHfMlrNBP5mjVrmNdjgq7BgJrwVQvQaHBCQwCZf6VeCCGESM7X1xdfX98M239YWBj58uUzJM4BAQFs3brVqE1oaCgBAQEZFkN6zZgxg/fffx+Azz77jFGjRjk4IiGEEI4kiXcmqEB+nNAYJd/O/ybSSe9gr1u3jq5du6LVaqnXpw0H51VFq9FIbW4hhBDZVkREBNHR0URERJCYmEhYWBgA5cuXx8PDg02bNnHr1i1ee+013NzcCA0N5bPPPuO9994z7GPgwIF8/fXXjBkzht69e7Nr1y5+/PFHtmzZ4qCjSt2cOXMYPXo0oJvVffz48Q6OSAghhKNJ4p0J/PBmASEMYBOJKLOJ9MaNG3nzzTdJTEyke/fuLF2wlL+dHnCZaKnNLYQQItuaOHEiy5cvN7yuXr06ALt37yYoKIjcuXPzzTffMGLECJRSlC9fnlmzZtGvXz/DNmXKlGHLli2MGDGCOXPm4Ofnx6JFi7JkKbF58+YxfPhwACZMmMDEiRMdG5AQQogsQaOS1usQZsXGxuLt7U1MTAxeXl427yeSGLOJ9NatW2nbti3Pnj2jS5cufP/99zg7O9sjdCGEEFmQvfoVYbnM+MwXLlxI//79ARgzZgzTpk1DozE3paoQQoicwJq+Re54ZyI/vE3uXG/fvp033niDZ8+e0bFjR1asWCFJtxBCCJHNLFu2jAEDBgAwYsQISbqFEEIYcXJ0AM+znTt30qZNG54+fUrbtm354YcfyJVLroUIIYQQ2cnKlSvp3bs3SimGDBnCzJkzJekWQghhRBJvB9m7dy8hISE8efKE1q1bs2bNGnLnzu3osIQQQghhhTVr1tCjRw+UUgwYMICvvvpKkm4hhBAmJPF2gAMHDtCqVSseP35MUPMmDFk7ndsujx0dlhBCCCGskLQaSZ8+fZg3b54k3UIIIcySxDuTHTlyhBYtWhAXF8dLTfzZ+3/+NHddTSm+ZDEnAd0kbLu5SiQxDo5WCCGEEMlFEsMnPy80qkayYMECnJzktEoIIYR58kBxJjp+/DjBwcE8ePCAgKB6HN4YiMqj+wq0KAawiWgeM44daFE4oWEBIfShhoMjF0IIIQTAYk7Sb+tMVIfVkKCldpdglixZIkm3EEKIVEkvkUnOnj1Ls2bNiImJoV69ekzY9C3K3fiZ7kQUYwlFi67Cmz4ZlzvfQgghhONFEkO/3V+h3lgDz7TQsRLHV9TmpvNDR4cmhBAii5M73pmkRIkSVKpUCa1Wy9atW4nx0OKExpBkAyavQZeMXybapAyZEEIIITLXJaJRFQtAmXzwYkH44Q20uZyknxZCCJEmSbwziZeXF7/++iuJiYl4enriCSwghAFsIhGFMxqm0YSx/w4z13NGQ3nyOy5wIYQQQgBQgfw4FfNCu68neLtBbmfpp4UQQlhEEu9M5OHhYfS6DzUIphyXiaY8+fHDm3zkMUrGvyNErqILIYQQWYAf3rqL5r7STwshhLCOJN4O5oe3UYdtLhkXQgghRNYg/bQQQghbSOKdBSVPxoUQQgiRdUg/LYQQwloyq7kQQgghhBBCCJGBJPEWQgghhBBCCCEykCTeQgghhBBCCCFEBpLEWwghhBBCCCGEyECSeAshhBBCCCGEEBlIEm8hhBBCCCGEECIDSeIthBBCCCGEEEJkIEm8hRBCCCGEEEKIDCSJtxBCCCGEEEIIkYEk8RZCCCGEEEIIITKQJN5CCCGEEEIIIUQGksRbCCGEEEIIIYTIQJJ4CyGEEEIIIYQQGSiXowPIDpRSAMTGxjo4EiGEEDmBvj/R9y8i40lfLoQQwt6s6c8l8bbAgwcPAChRooSDIxFCCJGTPHjwAG9vb0eH8VyQvlwIIURGsaQ/1yi53J4mrVbL33//jaenJxqNxtHhGMTGxlKiRAmuX7+Ol5eXo8Oxi5x4TJAzjysnHhPkzOOSY8p6lFI8ePCAYsWK4eQkT31lhqzUl2f3v9/0eJ6PHeT45fif3+PPqcduTX8ud7wt4OTkhJ+fn6PDSJGXl1eO+gOGnHlMkDOPKyceE+TM45JjylrkTnfmyop9eXb++02v5/nYQY5fjv/5Pf6ceOyW9udymV0IIYQQQgghhMhAkngLIYQQQgghhBAZSBLvbMzV1ZVJkybh6urq6FDsJiceE+TM48qJxwQ587jkmITIWp7nv9/n+dhBjl+O//k9/uf52PVkcjUhhBBCCCGEECIDyR1vIYQQQgghhBAiA0niLYQQQgghhBBCZCBJvIUQQgghhBBCiAwkibcQQgghhBBCCJGBJPHOhsLDw+nTpw9lypQhT548lCtXjkmTJhEfH2/U7vTp09SvXx83NzdKlCjBF1984aCILfPpp59Sp04d3N3d8fHxMdsmIiKCVq1a4e7uTqFChRg9ejQJCQmZG6iVvvnmG0qXLo2bmxv+/v4cPXrU0SFZZd++fYSEhFCsWDE0Gg0bNmwwWq+UYuLEiRQtWpQ8efLQpEkTLl265JhgLTR16lRq1aqFp6cnhQoVom3btly8eNGozZMnTxg8eDAFChTAw8OD9u3bc+vWLQdFnLZvv/2WV155BS8vL7y8vAgICOCXX34xrM9ux2POtGnT0Gg0DB8+3LAsJxyXyLks6dc0Go3Jz+rVq43a7Nmzhxo1auDq6kr58uVZtmxZxgdvB/bq17Pr8SdXunRpk+962rRpRm2y27mbNbL7+ZClPvroI5Pv+cUXXzSsz2n9lj3OE6Ojo+natSteXl74+PjQp08fHj58mIlHkTkk8c6GLly4gFar5bvvvuPs2bPMnj2b+fPn8/777xvaxMbG0qxZM0qVKsWJEyeYPn06H330EQsWLHBg5KmLj4+nY8eODBo0yOz6xMREWrVqRXx8PAcPHmT58uUsW7aMiRMnZnKklluzZg0jR45k0qRJnDx5kqpVqxIcHMzt27cdHZrF4uLiqFq1Kt98843Z9V988QVfffUV8+fP58iRI+TNm5fg4GCePHmSyZFabu/evQwePJjDhw8TGhrKs2fPaNasGXFxcYY2I0aMYNOmTfz000/s3buXv//+mzfeeMOBUafOz8+PadOmceLECY4fP06jRo1o06YNZ8+eBbLf8SR37NgxvvvuO1555RWj5dn9uETOlla/prd06VJu3rxp+Gnbtq1h3dWrV2nVqhUNGzYkLCyM4cOH07dvX7Zt25bB0aefPfr17Hz85kyZMsXou3733XcN67LjuZulcsL5kDVefvllo+/5t99+M6zLaf2WPc4Tu3btytmzZwkNDWXz5s3s27eP/v37Z9YhZB4lcoQvvvhClSlTxvB63rx5Kl++fOrp06eGZWPHjlUVK1Z0RHhWWbp0qfL29jZZvnXrVuXk5KSioqIMy7799lvl5eVldJxZSe3atdXgwYMNrxMTE1WxYsXU1KlTHRiV7QC1fv16w2utVquKFCmipk+fblh2//595erqqlatWuWACG1z+/ZtBai9e/cqpXTHkDt3bvXTTz8Z2pw/f14B6tChQ44K02r58uVTixYtyvbH8+DBA1WhQgUVGhqqGjRooIYNG6aUyjnfk8j5UurXlDL9dzW5MWPGqJdfftloWefOnVVwcLAdI8xY6enXc8Lx65UqVUrNnj07xfXZ+dwtLTntfCg1kyZNUlWrVjW7Lqf3W7acJ547d04B6tixY4Y2v/zyi9JoNOrGjRuZFntmkDveOURMTAz58+c3vD506BCBgYG4uLgYlgUHB3Px4kXu3bvniBDT7dChQ1SpUoXChQsblgUHBxMbG2u4q5eVxMfHc+LECZo0aWJY5uTkRJMmTTh06JADI7Ofq1evEhUVZXSM3t7e+Pv7Z6tjjImJATD8P3TixAmePXtmdFwvvvgiJUuWzBbHlZiYyOrVq4mLiyMgICDbH8/gwYNp1aqVUfyQ/b8nIfQGDx5MwYIFqV27NkuWLEEpZVh36NAhk7/94ODgHPE3bkm/ntOOf9q0aRQoUIDq1aszffp0o2H1OfHcDZ6P86HkLl26RLFixShbtixdu3YlIiICeP76LUvOEw8dOoSPjw+vvvqqoU2TJk1wcnLiyJEjmR5zRsrl6ABE+l2+fJm5c+cyY8YMw7KoqCjKlClj1E7fsUVFRZEvX75MjdEeoqKijDpnMD6mrObOnTskJiaajfnChQsOisq+9J+7uWPMit+JOVqtluHDh1O3bl0qV64M6I7LxcXF5JnErH5cZ86cISAggCdPnuDh4cH69eupVKkSYWFh2fJ4AFavXs3Jkyc5duyYybrs+j0JkdSUKVNo1KgR7u7ubN++nXfeeYeHDx8ydOhQIOW+LzY2lsePH5MnTx5HhG0XlvTrOen4hw4dSo0aNcifPz8HDx5k/Pjx3Lx5k1mzZgE589wNno/zoaT8/f1ZtmwZFStW5ObNm0yePJn69evzxx9/PHf9liXniVFRURQqVMhofa5cucifP3+O+0zkjncWMm7cOLOTrCT9Sf4P1I0bN2jevDkdO3akX79+Doo8ZbYckxCZafDgwfzxxx8mkxllRxUrViQsLIwjR44waNAgevTowblz5xwdls2uX7/OsGHD+OGHH3Bzc3N0OEIA9u/XPvzwQ+rWrUv16tUZO3YsY8aMYfr06Rl4BOkj/boxaz6PkSNHEhQUxCuvvMLAgQOZOXMmc+fO5enTpw4+CmFPLVq0oGPHjrzyyisEBwezdetW7t+/z48//ujo0ISDyR3vLGTUqFH07Nkz1TZly5Y1/P7333/TsGFD6tSpYzLxRpEiRUxmSNS/LlKkiH0CtoC1x5SaIkWKmMyA6YhjslTBggVxdnY2+z1kxXhtoT+OW7duUbRoUcPyW7duUa1aNQdFZbkhQ4YYJvHw8/MzLC9SpAjx8fHcv3/f6Kp0Vv/uXFxcKF++PAA1a9bk2LFjzJkzh86dO2fL4zlx4gS3b9+mRo0ahmWJiYns27ePr7/+mm3btmXL4xLZmz37NXP8/f35+OOPefr0Ka6urin2515eXg6525vZ/XpWO/7k0vN5+Pv7k5CQQHh4OBUrVswy52729jycD6XGx8eHF154gcuXL9O0adPnqt+y5DyxSJEiJpPsJSQkEB0dneM+E0m8sxBfX198fX0tanvjxg0aNmxIzZo1Wbp0KU5OxoMXAgIC+OCDD3j27Bm5c+cGIDQ0lIoVK2bqUCVrjiktAQEBfPrpp9y+fdswJCU0NBQvLy8qVapkl/ewJxcXF2rWrMnOnTsNM9RqtVp27tzJkCFDHBucnZQpU4YiRYqwc+dOwz+gsbGxhjuuWZVSinfffZf169ezZ88ek6F9NWvWJHfu3OzcuZP27dsDcPHiRSIiIggICHBEyDbRarU8ffo02x5P48aNOXPmjNGyXr168eKLLzJ27FhKlCiRLY9LZG/27NfMCQsLI1++fLi6ugK6vm/r1q1GbUJDQx32N57Z/XpWO/7k0vN5hIWF4eTkZDj2rHLuZm/Pw/lQah4+fMiVK1fo1q1btu2PbWXJeWJAQAD379/nxIkT1KxZE4Bdu3ah1Wrx9/d3VOgZw9GzuwnrRUZGqvLly6vGjRuryMhIdfPmTcOP3v3791XhwoVVt27d1B9//KFWr16t3N3d1XfffefAyFN37do1derUKTV58mTl4eGhTp06pU6dOqUePHiglFIqISFBVa5cWTVr1kyFhYWpX3/9Vfn6+qrx48c7OPKUrV69Wrm6uqply5apc+fOqf79+ysfHx+jGVyzugcPHhi+C0DNmjVLnTp1Sl27dk0ppdS0adOUj4+P2rhxozp9+rRq06aNKlOmjHr8+LGDI0/ZoEGDlLe3t9qzZ4/R/z+PHj0ytBk4cKAqWbKk2rVrlzp+/LgKCAhQAQEBDow6dePGjVN79+5VV69eVadPn1bjxo1TGo1Gbd++XSmV/Y4nJUlnNVcq5xyXyJnS6td+/vlntXDhQnXmzBl16dIlNW/ePOXu7q4mTpxo2Mdff/2l3N3d1ejRo9X58+fVN998o5ydndWvv/7qqMOymD369ex8/EkdPHhQzZ49W4WFhakrV66olStXKl9fX9W9e3dDm+x47mapnHA+ZKlRo0apPXv2qKtXr6oDBw6oJk2aqIIFC6rbt28rpXJev2WP88TmzZur6tWrqyNHjqjffvtNVahQQXXp0sVRh5RhJPHOhpYuXaoAsz9J/f7776pevXrK1dVVFS9eXE2bNs1BEVumR48eZo9p9+7dhjbh4eGqRYsWKk+ePKpgwYJq1KhR6tmzZ44L2gJz585VJUuWVC4uLqp27drq8OHDjg7JKrt37zb7vfTo0UMppSsV8eGHH6rChQsrV1dX1bhxY3Xx4kXHBp2GlP7/Wbp0qaHN48eP1TvvvKPy5cun3N3dVbt27YwubmU1vXv3VqVKlVIuLi7K19dXNW7c2JB0K5X9jiclyRPvnHJcImdKq1/75ZdfVLVq1ZSHh4fKmzevqlq1qpo/f75KTEw02s/u3btVtWrVlIuLiypbtqzRv1VZmb369ex6/EmdOHFC+fv7K29vb+Xm5qZeeukl9dlnn6knT54Ytctu527WyO7nQ5bq3LmzKlq0qHJxcVHFixdXnTt3VpcvXzasz2n9lj3OE+/evau6dOmiPDw8lJeXl+rVq5fhAl1OolEqSc0KIYQQQgghhBBC2JXMai6EEEIIIYQQQmQgSbyFEEIIIYQQQogMJIm3EEIIIYQQQgiRgSTxFkIIIYQQQgghMpAk3kIIIYQQQgghRAaSxFsIIYQQQgghhMhAkngLIYQQQgghhBAZSBJvIYQQQgghhBAiA0niLbKkS5cu0a5dO4oWLYqTkxM+Pj6ODknkUEopatasSbNmzYyWBwUFodFoHBRV1ovDEuZi3bFjBxqNhq1btzooKiGEEEIIx5PEW1glPDwcjUZj9JM7d26KFy9Op06dOH78eLrfIzExkbZt27J161ZatWrFxIkTGTdunB2ifz589NFHJt9R8p+PPvrI0WFmGStWrODkyZNMmTLF0aHYZO3atWg0GjZv3uzoUMxq0qQJ9erVY8yYMSQmJjo6HCGEEEIIh8jl6ABE9lSuXDnefvttAOLi4jhx4gQ//fQTGzZsYMeOHQQGBtq876tXr3Lu3Dn69evHggUL7BXyc6d9+/ZUrlzZ7LqgoKDMDSaL0mq1fPTRR9SvX5/XXnvN0eHYZOPGjeTNm5cmTZo4OpQUjRkzhtdff53Vq1fTtWtXR4cjhBBCiFRotVr+7//+jxs3btC6dWvKlSvn6JByBEm8hU3Kly9vctd02rRpjB8/ng8//JC9e/favO+///4bgGLFiqUnxOdehw4dePPNNx0dRpb2yy+/EB4ezgcffODoUGySkJDAli1bCA4Oxs3NzdHhpKh58+YULFiQ+fPnS+IthBBCZHFvvPEGGzduBOCDDz5g9+7d1KpVy8FRZX8y1FzYTZ8+fQA4ceKEybr4+HhmzZpFjRo1yJs3L56entSvX5+ff/7ZqF3p0qVp0KABAJMnTzY7NNrSfQH07NkTjUbDX3/9xcyZM6lUqRKurq707NnT0Ob27duMGDGC8uXL4+rqSsGCBWnfvj1//PGHyf5Kly5N6dKlefjwIcOGDaNYsWK4urryyiuvsHbtWrOfS3x8PLNnz6ZWrVp4enri4eFBpUqVGDlyJPfu3TNqa00s9rJs2TI0Gg3Lli1j+/bt1KlTB3d3dwoUKECPHj24e/eu2e1Onz7Nm2++SdGiRXFxcaFUqVK8++67Ju31jyf07NmT8+fP065dOwoUKIBGoyE8PByAR48eMWbMGEqUKIGbmxuVK1dm4cKF7Nmzx+j7j4mJIW/evLz88stmY9JqtZQuXZp8+fLx+PHjNI996dKlaDQa2rdvb/HntWbNGlxdXalatSo3b940LFdKsXTpUurXr4+Pjw/u7u5UqFCBAQMGEBERYWh34sQJhgwZQuXKlfH29iZPnjxUqVKFadOm8ezZM4vjANi/fz/37t2jTZs2hmX656yfPn3K+++/T8mSJcmTJw81a9Zkx44dgO5zHDx4MMWKFcPNzY2AgACOHj1q9j3++OMPOnXqRKFChXB1daVMmTIMHz48xb8Lc3Lnzk3btm357bffuHz5slXHKIQQQojMc/ToUTZt2sSmTZuIjo6mQYMGTJw40dFh5Qhyx1vYXa5cxn9WT58+pXnz5uzZs4dq1arRp08fnj17xpYtW2jTpg1z585lyJAhAAwfPpywsDCWL19OgwYNDEOi9f+1Zl9Jvfvuuxw+fJhWrVoREhJCoUKFALhy5QpBQUFERkbSrFkz2rZty+3bt1m3bh3btm1j586d+Pv7G+3r2bNnNGvWjHv37tG+fXsePXrE6tWr6dSpE7/++qvRJF2PHz+madOmHDhwgAoVKtCrVy9cXV25dOkS3333Hd27dydfvnw2x2JPP//8M1u2bCEkJIQ6deqwb98+VqxYwZUrV/jtt99M2nbq1AknJyfatGlDiRIlOHfuHF9//TXbtm3jyJEjhuPSu3z5Mq+99hpVqlShZ8+e3L17FxcXFxITE2ndujW7d++mSpUqvPXWW0RHRzNq1CiTIfHe3t68+eabLFmyhIMHD1KnTh2j9aGhoVy7do3BgweTJ0+eVI9XKcXu3bupWLGiSawpmTt3LsOGDTNc6PH29gZ0CX/nzp1Zu3YtxYsXp0uXLnh5eREeHs6PP/5IixYtKFmyJAALFy5k06ZNBAYG0rJlSx49esSePXsYP348x44dY926dRbFArBhwwacnZ1p3bq1ybrOnTtz5swZXn/9dR4/fswPP/xA69atOXDgAP379yc+Pp6OHTvyzz//sGbNGpo3b87Vq1cNxwTw22+/ERwcTHx8PB06dKB06dIcOnSIOXPmsHnzZg4fPkzBggUtijUgIIBFixaxa9cuypcvb/ExCiGEECLz3Lp1i5IlSxrOLXr16sX777/v4KhyCCWEFa5evaoAFRwcbLLus88+U4Bq1aqV0fL3339fAerDDz9UWq3WsDw2Nla9+uqrysXFRd24ccOwfPfu3QpQkyZNMnkPa/fVo0cPBSg/Pz917do1k/3VqVNHOTs7q19//dVo+cWLF5Wnp6eqUqWK0fJSpUopQLVp00Y9ffrUsHzHjh1mP5dRo0YpQHXr1k0lJCQYrbt//7568OCBzbGkZNKkSQpQ7du3V5MmTTL7c/PmTUP7pUuXKkDlypVL/fbbb4blCQkJKigoSAHq0KFDhuV37txRXl5eqnjx4io8PNzovVetWqUANWTIEMMy/d8MoCZOnGgS76JFixSgWrRoYfQZnT17Vrm5uZn8LRw5ckQBqmfPnib76tChgwJUWFhYmp/T2bNnFaC6du1qdn2DBg1U0n8i9X977dq1U48fPzZqO3fuXAWoxo0bq0ePHhmte/Tokbp7967h9bVr10z+FrRarerdu7cCjL4Dc3EkVbp0aRUUFGS2fb169dTDhw8Ny9esWaMA5ePjozp27KiePXtmWPf5558rQM2cOdOwLDExUZUrV04BJn+To0ePVoDq3bu3xbH+/vvvClDdu3c3u14IkXPEx8erSZMmqfLlyysXFxcFqPXr1zs6LJGFabVaVaNGDdW0aVOj5amdE2Ym/blMjx49HBqHJdIb671791SpUqXUpk2bVHR0tGrZsqV68803jdpcuHBBOTs7q2+++cYOET8/JPEWVtH/z1yuXDlDEvfee++phg0bKkAVLlxYnTt3ztA+MTFR5cuXT5UrV84oUdb7+eefFaDmzp1rWJbSP7K27EufeM+ZM8ek/cmTJ80mD3ojR45UgDpz5oxhmT7x/uuvv0zalypVSuXPn9/w+tmzZ8rT01N5e3ur6Ohos++RnlhSok+8U/s5deqUob0+8TaXEOnXffXVV4Zls2bNUoBasWKF2fevUaOGKliwoOG1/m+mSJEiRhcr9PTJ/cmTJ03W9e/f3+zfQvXq1VXevHlVTEyMYdnt27eVi4uLqlWrVoqfTVLbtm1TgBo5cqTZ9fokMiEhQfXp00cBql+/fiZJs1JKvfTSS8rZ2Vn9+eefFr23OSdOnFCA+uijj8zGkVxYWJgC1OzZs82237t3r9HyxMRElTt3bgWYXISKiIgw+RvYt2+f4YJIcg8ePFD58+dXbm5uRt9paol3VFSUAlSjRo3MfwBCiAyX9EKo/idXrlyqWLFiqmPHjurYsWN2eZ+pU6cqQAUGBqr3339fTZo0SZ0/f94u+87pzH1HyX/u3bvn6DDtbtmyZSYX+pXKPon3sWPHTM5BHcUesX7xxReGv7eKFSuqyMhIkzZvv/22KlSokIqNjbVX6DmeDDUXNrly5QqTJ082WlakSBH2799vNIz04sWL3Lt3j2LFipm0B/jnn38AuHDhQprvmZ591a5d22TZ4cOHAd2QGnPltfT7uXDhgtHs4D4+PpQpU8akvZ+fH4cOHTLa/sGDBzRp0iTNocy2xpKaVatWWTW5Ws2aNU2W+fn5AXD//n2TWI8cOcKVK1dMtnny5Al37tzhzp07RsOQq1atiouLi0n733//nbx581K9enWTdXXr1jU7s/2AAQMYOHAg//vf/xg4cCCgKwsWHx9Pv3790jhSHf0zymnViG/fvj0bN27kgw8+4JNPPjFZ//DhQ86fP0/58uWpUKFCmu8bHx/P119/zerVq7lw4QIPHz5EKWVYr59cMC36SU+SPt+dVLVq1YxeOzk5UahQIR49emQY9q5XtGhRk/c+deoUYH4GfA8PD1599VW2b9/OxYsXqVKlSprx5s+fH4A7d+6k2VYIkbEysjIJwObNm/Hw8CA0NNTsv/sibUm/o+Sy8mSatsgpFUYg5T45K0kr1gcPHjBz5kw0Gg1KKapXr07x4sVN2o0ZM4aVK1fy1VdfZdtJajObJN7CJsHBwfz666+ALuFdvnw5Y8eO5fXXX+fo0aN4eHgAEB0dDcDZs2c5e/ZsivuLi4tL8z3Ts6/ChQunuL8tW7awZcsWi/eX9BnYpHLlyoVWqzW8jomJATD7j5W9YrEnLy8vk2X65/WT1l/Wx/rNN9+kur+4uDijxNvcdwAQGxtLiRIlzK5LaZu33nqL9957j0WLFhkS78WLF+Ph4UGXLl1SjUtP/wz4kydPUm23b98+3NzcaNmypdn11nzPoJttftOmTbzwwgt07tyZQoUKkTt3bu7fv8+cOXN4+vSpRfvZsGEDVapUMXsRCFL+PlP7npNO7hYbGwuk/B3ok3V9u7ToJ7tzd3e3qL0QIuNkZGUS0F3EK1CggCTd6WDuO8qpsnuFEdAlszVq1EjxfCYrSSvWzz77jFu3bjFixAi++uorwsLCzLarUqUKr7zyCgsXLmT8+PE4Ocmc3WmRT0ikm6+vL++99x7vv/8+58+fZ8KECYZ1+pP89u3bo3SPNpj9Wbp0aZrvk559aTSaFPc3d+7cVPfXo0cPmz4X/Z3UGzduWHxsGRWLPeljPXPmTKqxlipVymg7c9+Bfn/60QrJ3bp1y+xyT09PunbtyokTJwgLC+PAgQOcP3+eN99803DRJy2+vr7AfxcSUrJz507c3d1p3rw5Bw8eNFmvvxBjyfd87NgxNm3aRHBwMOfOnWPhwoV8+umnfPTRR1aNToiIiODUqVO0bdvW4m2spf+eU/oOoqKijNqlRf856z93IUTWklplEtBdhAwJCaFgwYK4urpSoUIFJkyYwKNHjwxtPvroIzQaDVevXuXatWuGyiSlS5e2el+AUWWLgwcP0qxZM3x8fEz6E1v2d/z4cZo2bYqnpyfe3t60a9fOUGnD3LG3bduWwoUL4+rqSokSJXjjjTdMJh61JhZ7Wrp0Kf7+/nh4eODh4YG/vz/Lli0zaWfN55mZx2tLhZGYmBgaNGiAk5MTc+fOtTr++Ph45s6dS3BwMCVKlMDV1ZVChQrxxhtvGEZ8Werq1aucOXPG6A5y8s+6YcOGeHp64uvryzvvvGO4GL1lyxYCAgLImzcvhQsXZsyYMSQkJJh9H0u/Z2tjTSo8PJzZs2dTqFAhJk+eTPny5bl06VKKlWI6derEtWvX2L17t1VxPK8k8RZ28/7771OsWDHmzZtn6LxeeuklvLy8OH78uNWlkpKz574AwwzhSYeH21PFihXx8vLi2LFjJmXDMjsWe7J3rFWrViUuLs7sFVVzia7egAEDAN0s4YsWLQKweJg5wMsvv4yTkxMXL15MtV316tXZtWsXLi4uNG/enAMHDhit15eHu3r1KpcuXUp1X/qh+a1atcLZ2dlo3f79+y2OXV86LyOHtOmH/u/Zs8dkXVxcHMePHydPnjxUrFjRov3pP2dLhqULIRwneWUSgG+//ZagoCAOHDhAq1atGDp0KH5+fnz66ac0bdqU+Ph4QPdoyqRJk/D29sbb25tJkyYxadIkhg8fbvW+kjp48KChVGL//v3p3LlzuvZ37NgxAgMDcXFxYcCAAbz66qts2LCBJk2amIyCmjNnDkFBQYSGhtK0aVNGjRpFo0aN+P33303KiNoSS3oNHTqU3r17c+PGDfr06UOfPn24ceMGvXr1YtiwYWa3Se3zzOzjVTZUGLl58yaBgYEcPnyYVatW8e6771odf3R0NMOHD+fp06e0bNmSESNGEBQUxNatW6lTpw7Hjh2zKBbQjUAD833ykSNHaNy4Md7e3gwYMICSJUvy7bff0q9fP9asWUOHDh0oVaoUAwYMwMfHh+nTp/PZZ5+Z7MeW79naWAHGjh3L06dPmTJlCp6enlSuXJnExEROnz5ttn1AQACgu0khLJCRD5CLnCe1Wc2VUmrOnDkmk4SNHTtWAWro0KEqPj7eZJszZ86oW7duGV6nNpGGtfvST6529epVs/H6+/srjUajVq9ebbIuMTFR7dmzx2hZqVKlVKlSpczuy9zEUvrZny2Z1dzaWFKin1xt1apVFrXXT6C2dOlSk3Xmvovbt28rT09P5evrq/744w+TbeLi4owmR0lrko+FCxcaZsNPTEw0LD9//rzZWc2TqlWrlvL29lZ58+ZVr7zyikXHm1S1atWUp6en0fvqJf8+f//9d1WwYEHl4eGh9u/fb9T2m2++UYBq0qSJyazmjx8/NsxqfvDgQQWoTp06GbX5448/VL58+cx+Tub+rpo0aaL8/PzMHlNqE5yl9vcLqAYNGhheJ53VPDQ01KjtuHHjrJ7VfPLkyQpQ27ZtM7teCJHxbKlMcvbsWZUrVy5VtWpVdefOHaN1+knUZsyYYbQ8pX9rrN2Xvg8C1JIlS+y6v+R9bbdu3Uz6zrCwMOXk5KSKFStmch6h1WqNqqjY8jmZY24S26Q/SfvXvXv3KkC99NJL6v79+4bl0dHR6oUXXlCA2rdvn9njN/d5OuJ406owkvw85OLFi6p06dLK09PTpG+yJv4nT56YnTDsjz/+UB4eHqpJkyZGy1M7l2nQoIEqXbq02bgBtWHDBsPy+Ph49corryiNRqMKFiyojh49algXGxurChUqpPLnz290jmvt92xtrHoHDhxQgKpUqZLhnFV/Tjl//nyz28TExBgmUhRpk8RbWCWtxPvx48eqWLFiKleuXOry5ctKKd0/bk2bNjV0JL169VJjx45Vb7/9tqpatarJLJapJd7W7iutxPuvv/4yzFT+2muvqXfeeUeNGjVKdezYUfn5+SlXV1ej9tYm3o8fP1b169dXgKpQoYIaOnSoGj16tGrfvr3Kmzev0ezi1saSEkvKiSU9sbA28VZKqc2bN6s8efIoZ2dn1apVKzVq1Cg1ZMgQ1bp1a+Xp6Wn095FW4p2QkKACAwMVoF555RU1duxY1a9fP+Xp6alCQkIUoCZPnmx228WLFxs6NltmEtUngwcOHDBZZ+77PH36tPL19VUeHh5GnZxWq1WdOnVSgCpevLgaNGiQGjt2rOrSpYvKnz+/oYxOQkKCql27tgJU/fr11ejRo1Xnzp1Vnjx5DKXQ0kq87927p3Lnzq3eeecds8dkr8RbKaX279+v3N3dVe7cudVbb72lxo8fb5iFvly5cur27dsWv3e9evVUvnz5TEqxCSEyj7WVSZRSaujQoSYn9nqJiYnK19dX1axZ02h5Sv/WWLsvfR9Uo0YNs8dj6/7MJQn6dUkrXQwaNCjFJDW9saQkrVnNk1ay0JehXLNmjcl+fvjhB5MLpGl9no443rQqjCQ9Dzl69Kjy9fVVvr6+6vjx4+mKPzUhISHKxcXFKPlN6Vzmzp07ytnZWQ0bNsxs3A0bNjTZ/5QpUxSgevXqZbJO/50mrZ5j7fdsbaxK6c5j9OcnW7duNSxfu3atAtTAgQNNttFzc3NTZcuWTXG9+I9Mribsys3NjfHjx/Puu+8yefJkVqxYgaurK7/88guLFy9mxYoVrFu3jqdPn1K4cGEqVarEwIEDLR5+as99AZQpU4ZTp04xa9YsNmzYwNKlS3F2dqZo0aIEBgbSoUMHWz8KQPd5hIaG8vXXX7Ny5UoWLlyIs7MzJUuWZODAgUbPvdk7lnXr1rFu3Tqz69q0aWPVM8XJtWrVilOnTjF9+nR27NhBaGgoefPmxc/Pj169eqU4E6s5zs7ObN26lUmTJrFq1Sq+/PJLypUrx8yZM8mfPz+bNm1K8TniN998k3feeQcnJyer3lOvb9++fPzxx6xcuZI6deqk2b5KlSrs2rWLxo0b06JFC7Zu3UpgYCAajYbVq1fTrFkzFi1axIoVK1BKUbx4cTp16mSYMd7Z2ZnNmzczbtw4fv31V44dO0aFChWYMWMGLVq0MBnGZ87WrVt59uxZhj7frVevXj0OHz7MlClT2L59OzExMRQrVoxhw4YxYcIEo8nzUhMeHs6BAwcYNmxYjpuNV4jsyNLKJPBfJYtt27aZHU6aO3duiyqTpGdftWrVsuv+LK3icfToUQCaNWtm9v3tEUtKkk5im5LUqk80bNgQwOxjXCl9no44XksrjOzfv5+ZM2fi6+vLtm3bzFYRsSZ+0H02X3zxBb/99htRUVEmjzHeuXPHMJFoSrZs2UJiYqLFFUbgv8lJU1v3999/GyZPtfV7tibW//3vfxw9epSmTZvSokULw3J9JZ3U9p8/f36pWGIpR2f+QgiRkg8++MDk6mtS+lqU3bp1s/k93n77bZUvX75sU4eyU6dOytvb2+yjFlnVBx98oHLnzm0YBSOEcAxzo9Zu376tpk+frpycnNRLL71k9AiUUkqVL18+1Tuw+p+kUrrjbe2+9HcNJ06caPZ4bN2fuRF15u4Sli9fXmk0GrOPI6U3lpSkNbIwqXLlyiknJyel1WpN1iUmJiqNRqPKly9vWGbJ55nZx7t+/XoFqPfff9/sen3M+sex3njjDZNH92yJ/8CBA8rV1VW5urqqkJAQNXLkSDVx4kQ1adIkwwjKpKMlU7qL3K5dO5U/f3717Nkzs3Gb+1tLbaShftTi7t27Dcus/Z6tjfXRo0eqRIkSysnJSf3+++9G6xISEpSbm5vKmzdvip9rvnz5VJEiRcyuE8ZkcjUhhMPdvHnTZNm5c+f46quv8PHxMXuVF2D69OkADBo0yOb3/uSTT3j8+LHJrKhZUXx8PL/++istWrQgd+7cjg7HIvfu3WPu3LkMGjSIcuXKOTocIUQyqVUmgf8qF8TGxqZaycIStu4rtaoY9orNHB8fH5RSZvuozI4lpffUarVmK4Pcvn0bpZTZEWMpfZ6OOF5LK4wMGTKEPn368H//93+89dZbZmf+tib+Tz/9lKdPn7Jjxw5+/vlnZs6cyeTJk/noo48oUqRImtuDrhzp9u3badWqldlJCe3F1u85qdRinTFjBtevX0er1VK1alVDNQKNRkOuXLl48uQJcXFxZieQ1Wq1xMTESMUSC0niLYRwuEGDBlGtWjX69+/P2LFj6dChA9WrV+fhw4fMmjXLUHMbdKW0pk2bRrdu3fjxxx8JDg42zKppi1KlSrF8+XI8PT3tcSgZysXFhZiYGFatWuXoUCx29epVRowYwcSJEx0dihAiFeYqk8B/lSz0Q4vTw577yoj9JVe7dm0Atm/f7vBYzEmt+oR+mbnhzClxxPFaWmHEycmJhQsX0q9fP3788Ue6du1qknxbE/+VK1fInz8/9erVM1r+6NEjTp48aVHsO3bsIC4uLkMrjIB9vueUYr158yZffPEFefPmNcyWnvzn5ZdfBswPN7906RJarVYqllgq426mCyGEZVauXKnq1aunChQooHLlyqV8fHxU06ZN1a+//mrSVj98y8PDQ4WEhKibN286IGIhhMh+bKlMcubMGZUrVy5VsWJFde3aNZNt7t27p06ePGm0LKWh5tbuK7Xhuvben7nhuadPn1bOzs6qWLFiKjw83Kh98lmybfmczLFmqLl+tutKlSqpmJgYw/L79++rF198UQFq7969huVpfZ6OOF6lUq8wkjxmrVarBgwYoADVoUMHo2HT1sTfrFkzpdFojKqzJCQkGCZow4Kh5n379lWurq4mj2eYizspa4eaW/s9WxNrr169FKCmTp1qEoverFmzFKDGjRtnsm758uUKUN99912K24v/yORqQgiH69q1K127drWobVBQkN2H6wkhhID+/fvz+eefs2LFCt5//33KlStH5cqVmTdvHoMGDaJixYq0bNmScuXK8eDBA/766y/27t1Lz549mT9/fpr7t+e+MmJ/yVWpUoUvv/ySoUOH8vLLL9O2bVtKlSpFVFQU+/bto1WrVnz55ZeZEos5gYGBvPvuu8ydO5fKlSvTvn17lFKsW7eOyMhIhg4dSmBgYJY/3nbt2jFp0iQOHz6c5kSnGo2Gb7/9FicnJ7799luUUqxevZpcuXJZFf+7777L9u3bqVevHp06dcLNzY09e/Zw48YNgoKCzN5dTkqr1bJp0yYaN26Mh4eHJR+vzdL7PacU66lTp1i+fDkvvPACI0eOTHH71O54h4aGkitXLlq3bm37AT5PHJv3CyGEEEKIzGDJ3dS5c+eanbTy6NGj6s0331TFihVTuXPnVgULFlQ1atRQ48aNU+fPnzdqm1rpQmv2ldYdWnvuL7XSl7t371atW7dW+fPnVy4uLsrPz0+1b9/ebClKaz4nc6y54623ZMkSVatWLeXu7q7c3d1VrVq1zJbUsvTzzMzjVUqpGzduqFy5cqlBgwZZHLNWq1WDBw82TLiWdMJRS+Nfu3atqlGjhnJ3d1cFCxZUnTp1UleuXDFbijb534e+5vWCBQtS/AxT+qytveOtZ+n3bGms+vKgv/zyi9lj0Ltx44YCTCZQi4uLUx4eHqpt27apbi/+o1FKbh0JIYQQQgghHKNbt25s2bKFa9euZYs5V8aOHcv06dP5+++/LZ6MzVEyKtZFixbRr18/9u7da9XIiueZJN5CCCGEEEIIh7l27RovvvgiH374Ie+//76jw0nTiy++SL58+Th06JCjQ0lTRsSakJDACy+8QJUqVdi4caPd9pvTyTPeQgghhBBCCIfRVxi5deuWo0OxyIULFxwdgsUyItaIiAi6d+9Ot27d7L7vnEzueAshhBBCCCGEEBlI6ngLIYQQQgghhBAZSBJvIYQQQgghhBAiA0niLYQQQgghhBBCZCBJvIUQQgghhBBCiAwkibcQQgghhBBCCJGBJPEWQgghhBBCCCEykCTeQgghhBBCCCFEBpLEWwghhBBCCCGEyECSeAshhBBCCCGEEBno/wGa4z7joh3aWgAAAABJRU5ErkJggg==\n"
},
"metadata": {}
}
],
"source": [
"import matplotlib.pyplot as plt\n",
"\n",
"fig, ax = plt.subplots(1,2,figsize=(10,5))\n",
"\n",
"e1 = energy.cpu().detach().numpy() + np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy_sqm.npy\",\"rb\")) * 27.2114 * 23.061\n",
"e2 = ene_pred.cpu().detach().numpy() + np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy_sqm.npy\",\"rb\")) * 27.2114 * 23.061\n",
"\n",
"ax[0].plot(e1, e2, linestyle='none', marker='.', color='springgreen')\n",
"ax[0].plot([np.max(e1), np.min(e1)], [np.max(e2), np.min(e2)] , color=\"k\", linewidth=1.5)\n",
"ax[0].set_xlabel(\"Reference Energy (kcal/mol)\", size=14)\n",
"ax[0].set_ylabel(\"Predicted Energy (kcal/mol)\", size=14)\n",
"ax[0].annotate('RMSD: %.3f' % np.sqrt(np.mean((e1 - e2)**2)), xy=(0.05, 0.95), xycoords='axes fraction', size=14)\n",
"\n",
"f1 = -qm_gradient.cpu().detach().numpy().reshape(-1) - np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad_sqm.npy\",\"rb\")).reshape(-1) * 27.2114 * 23.061 / 0.529177249\n",
"f2 = -grad_pred.cpu().detach().numpy().reshape(-1) - np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad_sqm.npy\",\"rb\")).reshape(-1) * 27.2114 * 23.061 / 0.529177249\n",
"\n",
"ax[1].plot(f1, f2, linestyle='none', marker='.', color='springgreen')\n",
"ax[1].plot([np.max(f1), np.min(f1)], [np.max(f2), np.min(f2)] , color=\"k\", linewidth=1.5)\n",
"ax[1].set_xlabel(r'Reference Force (kcal/mol/$\\AA$)', size=14)\n",
"ax[1].set_ylabel(r'Predicted Force (kcal/mol/$\\AA$)', size=14)\n",
"ax[1].annotate('RMSD: %.3f' % np.sqrt(np.mean((f1 - f2)**2)), xy=(0.05, 0.95), xycoords='axes fraction', size=14)\n",
"\n",
"plt.tight_layout()\n",
"plt.savefig('rmsd.png', dpi=300)"
]
},
{
"cell_type": "markdown",
"source": [
"### The Model Weights and Biases Dictionary\n",
"\n",
"This cell prints the size of the weights and biases used in the trained model for reference."
],
"metadata": {
"id": "Ifal2I5wMDU8"
}
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"id": "RLr5VkQCPoBO",
"colab": {
"base_uri": "https://localhost:8080/"
},
"outputId": "8d6124b9-4c62-4bb9-b340-68777627976e"
},
"outputs": [
{
"output_type": "stream",
"name": "stdout",
"text": [
"Model's state_dict:\n",
"fitting_net.fitting_net.0.weight \t torch.Size([3, 240, 48])\n",
"fitting_net.fitting_net.0.bias \t torch.Size([3, 240])\n",
"fitting_net.fitting_net.1.weight \t torch.Size([3, 240, 240])\n",
"fitting_net.fitting_net.1.bias \t torch.Size([3, 240])\n",
"fitting_net.fitting_net.2.weight \t torch.Size([3, 240, 240])\n",
"fitting_net.fitting_net.2.bias \t torch.Size([3, 240])\n",
"fitting_net.fitting_net.3.weight \t torch.Size([3, 1, 240])\n",
"fitting_net.fitting_net.3.bias \t torch.Size([3, 1])\n"
]
}
],
"source": [
"print(\"Model's state_dict:\")\n",
"for param_tensor in model.state_dict():\n",
" print(param_tensor, \"\\t\", model.state_dict()[param_tensor].size())"
]
},
{
"cell_type": "markdown",
"source": [
"## Plotting the Minimization of the Loss Function"
],
"metadata": {
"id": "kM7z96Vswymb"
}
},
{
"cell_type": "markdown",
"source": [
"### Plotting Validation Error for $\\Delta$MLP\n",
"\n",
"Validation error for the $\\Delta$MLP is shown below."
],
"metadata": {
"id": "fnqPBH5iMI3p"
}
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"id": "xzYcSyS4PrE2",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 855
},
"outputId": "e6411291-147d-466c-c680-858cf25c05c0"
},
"outputs": [
{
"output_type": "display_data",
"data": {
"text/plain": [
""
],
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAj4AAANGCAYAAAD9NIS0AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAC29ElEQVR4nOzdd1yW9eL/8dcNiLjAjYKCeyuaipoTtIxS02xq6dHK6qedks5pnWN7nsZJy8a3HA07WuYoy9Rw5Z6Ue5sKCuIAAQXhvn5/XIIioIwL7sH7+Xjcj3tc1319PtwW95vPtBmGYSAiIiJSBng4ugIiIiIipUXBR0RERMoMBR8REREpMxR8REREpMxQ8BEREZEyQ8FHREREygwFHxERESkzFHxERESkzPBydAXEZLfbiY2NpUqVKthsNkdXR0RExGUYhsG5c+cICAjAw+PabToKPk4iNjaW+vXrO7oaIiIiLuvo0aPUq1fvmuco+DiJKlWqAOY/mq+vr4NrIyIi4jqSkpKoX79+9nfptSj4OIms7i1fX18FHxERkSIoyFARDW4WERGRMkPBR0RERMoMBR8REREpMxR8REREpMxQ8BEREZEyQ8FHREREygwFHxERESkzFHxERESkzFDwERERkTJDwUdERETKDEu3rFi2bBlRUVGsXr2aY8eOkZCQQMWKFalVqxZt27ald+/eDBgwgDp16lhZrIiIiEiB2AzDMIpzgZSUFCZNmsTnn3/OX3/9RdblfHx8qF69OufPnycxMRG73Q5AuXLlGDhwIOPHj6d79+7F/wncRFJSEn5+fiQmJjrVXl1JabDuGPQOhvLa2U1ERJxQYb5Di9XV9emnn9KkSRP+9a9/4evry6uvvkpUVBSJiYmkpqZy7NgxTp06xcWLF9m9ezdffvkld999N4sXL6ZXr17ccccdHDp0qDhVkBL24QZ4eAHM2e3omoiIiBRfsYLP448/zk033cSff/5JdHQ0zz//PGFhYbm2hbfZbDRr1owHHniAr7/+mri4OD777DP++OMPvv7662L9AFKyjidfuj/n2HqIiIhYoVidFzt27KBZs2aFfl+FChV46KGHGDVqFEeOHClOFaSEpaSb9+czHFsPERERKxSrxacooedKnp6eNGzYsFjXkJKVetG8v6DgIyIibkDT2eWaUi4FH7X4iIiIOyhWV1dxuqmCgoKKU7SUErX4iIiIOylW8GnQoAE2m63Q77PZbGRk6JvUFWS3+Fx0bD1ERESsUKzgM2LEiCIFH3EdqRrcLCIibqRYwWf69OkWVUOckWFojI+IiLgXDW6WfKVlQualdb0vqKtLRETcQIltQhATE0N0dDRJSUn4+vrSvn17AgMDS6o4KQGpV4QdtfiIiIg7sDz47N+/n8cee4ylS5fmOta3b18+/vhjmjRpYnWxUgJSFHxERMTNWBp8jh49So8ePYiPj6dFixb06tWLunXrcuLECVauXMlvv/1Gz5492bBhA/Xr17eyaCkBV87k0qwuERFxB5YGn5dffpn4+Hg+/vhjHnnkkVwzvj777DMee+wxXnnlFT7//HMri5YScGWLj9bxERERd2Bp8Fm0aBEDBw7k0UcfzfP4I488wi+//MLChQutLFZKSNY+XXBpoLMdPDUcXkREXJilX2Px8fG0adPmmue0adOGkydPWlmslJDUq7q31OojIiKuztLgU6tWLXbu3HnNc3bu3EmtWrWsLFZKSMpVwUcDnEVExNVZGnz69+/Pjz/+yJQpU/I8PnXqVH766SduueUWK4uVEnJ1i4+Cj4iIuDqbYRiGVRc7cuQInTp14tSpU7Rq1YrevXvj7+9PXFwcK1euZMeOHdSsWZNNmzZpVtdVkpKS8PPzIzExEV9fX0dXB4D/2wKv/375+ZL7oVkNx9VHREQkL4X5DrV0cHNQUBCrV6/mkUceYfny5ezYsSPH8bCwMD755BOFHheRmp7zucb4iIiIq7N8AcOmTZuydOlSjh49mmvlZgUe16IxPiIi4m5KbMuK+vXrK+i4uFxjfLSIoYiIuLgSCz7ivAwDouNg9k5YdAD6BMO7N+c+T4ObRUTE3VgefA4dOsTEiRP5448/iI2N5eLF3M0ENpuNAwcOWF20XEdaBkyLhu92woEzl19fsC/v4KOuLhERcTeWBp9ff/2VwYMHk56eTrly5ahduzZeXrmLsHAimRTC3N3w5mrzsY8XhDeAX/abgSY9E7w9c55/dYtPmoKPiIi4OEuDzzPPPIOnpyezZs1i6NCheHhofwNn8leied+/Mbx3E1QsB40+NF87lwY1KuY8P6vFp7ynuWWFxviIiIirszSZ7N27l2HDhnHXXXeV+dCzYMECmjdvTtOmTfniiy8cXR0Ajieb9x3qQJXy5r5blb3N15LScp+fNZ291qVApK4uERFxdZa2+NSpUwcfHx8rL+mSMjIyiIyMZNmyZfj5+dGxY0eGDBlCjRqOXf3vxKXgU6fy5dd8vSE5Hc6l5z4/q8WnRkU4dk7BR0REXJ+lzTLDhg1j4cKFXLhwwcrLupwNGzbQunVrAgMDqVy5MhERESxevNjR1SIur+BT3rzPs8XnUvCpXsG8V1eXiIi4OkuDz0svvUSLFi3o378/q1evJjk52crL5/DWW29hs9l48sknLb3uypUrGThwIAEBAdhsNubNm5fneZMnT6ZBgwb4+PjQpUsXNmzYkH0sNjaWwMDA7OeBgYHExMRYWs/CMgw4kWI+rlPp8utVLgWfxDyCT1aLT81LwUcrN4uIiKuzNPiUK1eOv//972zbto1evXrh5+eHp6dnrlteM70KY+PGjXz22We0a9fumuetXr06z+n0O3fuJC4uLs/3pKSkEBISwuTJk/O97qxZs4iMjOTFF19ky5YthISE0L9/f+Lj4wv3g5Sic+mXW3DyavE5d1XwybRfDjo1NMZHRETchKVjfGbNmsXw4cOx2+00atSIunXrFjvkXC05OZnhw4fz+eef89prr+V7nt1uZ+zYsTRt2pSZM2fi6WnO1d6zZw/h4eFERkby9NNP53pfREQEERER16zD+++/z8MPP8yoUaMA+PTTT/n555+ZOnUqzz77LAEBATlaeGJiYggNDS3Kj2uZrPE9vuWhQrnLr2d3dV01xufKqezZwUddXSIi4uIsTSWvvPIKfn5+/Prrr3Tu3NnKS2cbO3Yst912G/369btm8PHw8OCXX36hV69ejBgxgq+//ppDhw4RHh7O4MGD8ww9BZGens7mzZt57rnncpTVr18/1q5dC0BoaCjbt28nJiYGPz8/Fi5cyIQJE/K83uTJk5k8eTKZmZlFqk9BZQWfupVzvp7fGJ+s4ONhg6qXzlGLj4iIuDpLg8+hQ4cYNWpUiYWemTNnsmXLFjZu3Fig8wMCAli6dCk9e/Zk2LBhrF27ln79+vHJJ58UuQ4JCQlkZmbi7++f43V/f392794NgJeXF++99x5hYWHY7XaefvrpfGd0jR07lrFjx5KUlISfn1+R63U9ec3oAqiSz3T2rOBTqZy53g8o+IiIiOuzNPjUr1+/xFoujh49yhNPPMGSJUsKNWU+KCiIr7/+mt69e9OoUSOmTJmCzWYrkTpeadCgQQwaNKjEyymorIHN/pVyvp7fGJ+sgc0Vy5mrPANcUFeXiIi4OEsHNz/88MP89NNPnD592srLArB582bi4+O54YYb8PLywsvLixUrVjBp0iS8vLzyDVxxcXGMGTOGgQMHkpqayvjx44tVj5o1a+Lp6ZlrcHRcXBx16tQp1rVLUl5T2eH6XV2Vrgg+avERERFXZ2mLz5133snq1avp3r07//73vwkJCcHX1zfPc4OCggp17b59+7Jt27Ycr40aNYoWLVpkb5VxtYSEBPr27UvLli35/vvv2bt3L3369KF8+fK8++67hSo/i7e3Nx07diQqKorBgwcD5kDqqKgoxo0bV6Rrlob8urryCz7ZLT7elwdDK/iIiIirszT4NGrUCJvNhmEYjBgxIt/zbDYbGRmF+xatUqUKbdq0yfFapUqVqFGjRq7XwQwjERERBAcHM2vWLLy8vGjVqhVLliwhPDycwMDAPFt/kpOT2b9/f/bzQ4cOER0dTfXq1bPDWmRkJCNHjqRTp06EhobywQcfkJKSkj3Lyxkdzy/4FGCMT4WsFh91dYmIiIuzNPiMGDGiVMbPFISHhwdvvPEGPXv2xNvbO/v1kJAQfvvtN2rVqpXn+zZt2kRYWFj288jISABGjhzJ9OnTAbjnnns4efIkL7zwAidOnKB9+/b8+uuvuQY8O5PrdXVdvWVFyqXnFbwuBx8tYCgiIq7O0uCTFQxKy/Lly695/Kabbsrz9Q4dOuT7nj59+mAYxnXLHjdunFN3bV0pPRMSzpuP6+QzuDm/rq5K6uoSERE3UuzBzR9//LHDt2OQa4u/NKPL2/PyvltZqlzR4pNpv/x66hWzurJafDLscLFklxsSEREpUcUOPuPGjSMoKIjOnTvz+uuv5xqALI6XNbC5diW4uieyyuVeQJKv6O5KyWNWF6jVR0REXFuxg8/GjRt5/vnnSU9PZ8KECbRv357GjRvz1FNPsWLFCux2+/UvIiUqv1WbAcp7XQ42V25bceXgZm9PcwVnUPARERHXVuzg07FjR1599VX++OMPDh48yLvvvktQUBCTJk0iPDwcf39/Ro0axbx580hNTbWizlJI+U1lz5LXOJ+swc0Vy5mtRBW0iKGIiLgBSxcwbNCgAePHj2fZsmXExcUxbdo0evbsyezZs7njjjuoWbMmAwcOZOrUqU69k7m7yW/V5ix5bVuR1bJT6dKxClrEUERE3IClwedK1atXZ8SIEcyZM4eEhAR+/PFHhg8fzqZNm3jooYcICAigR48eJVW8XCG/qexZ8tq24soWHwCfS/ea0i4iIq7M0uns+SlfvjwDBgxgwIABGIbBunXrmDdvHj/++GNpFF/mFaWr68oxPqAWHxERcQ8l1uKTH5vNRrdu3Xj77bfZtWtXaRdfJuW3anMWv7zG+FwxnR20erOIiLiHYrX4HDlypMjvLexeXVI0hnF5HZ/8gk9eY3xSrw4+WsRQRETcQLGCT4MGDYq0RUVR9uqSojlzAdIuLTqY3+Dm7K6ufNbxgctT3jXGR0REXFmxgo8z7c0lecsa31OjgrkeT17yHOOTNbj56lld6uoSEREXVqzgU9p7c0nhZQUf/3y6uSB38DGM3C0+6uoSERF3UOqDm6V0XWvV5ixVrgo+aZmQeWmf1lyDmxV8RETEhSn4uLnsqez5jO+BK9bxudS9lXpFd9bVwUcrN4uIiCuzfB2fzMxMvvvuO3777TdiY2NJS0vLdY7NZiMqKsrqoiUP2as2F6KrKyv4lPcEr0vR2EddXSIi4gYsDT4pKSncfPPNrFu3DsMwsNlsGIaRfTzruQZEl57rLV4IuaezZy9eeMXO7erqEhERd2BpV9drr73G2rVrefnll0lISMAwDF566SWOHz/OrFmzaNSoEXfddVeerUBSMq63XQVcXsDwXFrOgc1Z3VxweTq7ZnWJiIgrszT4zJkzh65du/Lvf/+b6tWrZ7/u7+/PXXfdxbJly/jtt9945513rCxWriGrq+tag5uzuroyDbO1J2ufrkpXBB+1+IiIiDuwNPgcOXKErl27Xr64h0eO1p169epx22238eWXX1pZrOTjQgacvWA+vtYYHx8vKHfpv4SktNyrNsPl6exawFBERFyZpcGnUqVKeHhcvqSfnx/Hjx/PcU6dOnWKtdWFFFzW+J4KXuDrnf95NlvOKe3q6hIREXdlafAJDg7OEWratGnD0qVLs1t9DMMgKiqKunXrWlms5OPKgc3XG0/ue8UA56t3Zgd1dYmIiHuwNPj07duXZcuWZe/DNXLkSI4cOUK3bt345z//SY8ePYiOjmbo0KFWFiv5KMiqzVmu3K8rrxYfrdwsIiLuwNLp7A8//DA1atTg5MmT1K1bl9GjR7N161Y+/vhjoqOjARg6dCgvvfSSlcVKPgoysDnLlWv5pF5jcLMWMBQREVdmafBp2rQpzzzzTI7XPvzwQ1544QUOHjxIcHAwderUsbJIuYaCrNqcJc8xPlrHR0RE3IzlKzfnpVatWtSqVas0ipIrFKWr61x+Y3zU1SUiIm7A0jE+O3fuZNKkSZw8eTLP4/Hx8UyaNIldu3ZZWazko2ZFaOAH9X2vf+6VY3zyms5+5ayuKxbjFhERcSmWtvi89dZbREVFMW7cuDyP16hRg3feeYetW7cybdo0K4uWPLwWVvBzffPo6sprjI8BpGdC+VJpKxQREbGWpS0+v//+O3379s2xls+VPD096du3LytXrrSyWLFAlTyms185xsfniqCjRQxFRMRVWRp8Tpw4Qf369a95TmBgYK5FDcXxrtyvK3tw8xVhp5zn5dWdNc5HRERcleUrN8fHx1/znPj4eHx8fKwsVixwvenscMXMLk1pFxERF2Vp8LnhhhuYN28eZ8+ezfP4mTNnmDt3LjfccIOVxYoF8hrjU/GqbS58NLNLRERcnKXBZ+zYsZw6dYqwsLBc43hWrFhBWFgYZ86cyXfwszhOXmN88m3xUfAREREXZencnNtvv53x48fz3//+l7CwMMqXL0+dOnU4ceIEaWlpGIbBP//5TwYPHmxlsWKB7HV80i/v61VRXV0iIuJmLG3xAXjvvff48ccf6d+/P5UqVeLYsWNUrlyZiIgIfv75Z95++22rixQLZAWftMzLs7Zytfhceq5ZXSIi4qpKZDWWAQMGMGDAgJK4tJSQSt5gw1yn58rXruSjri4REXFxlrb47N27t0DnzZ4928pixQIetsv7dWU9L++Z8xx1dYmIiKuzNPjcfPPN112jZ/bs2QwfPtzKYsUivlcEn0rlLo/1yaL9ukRExNVZGnzOnj1L//79SUxMzPP4nDlzGDZsGA0bNrSyWLHIlcHn6oHNoK4uERFxfZYGn3nz5rFv3z4GDhxIWlpajmNz587l3nvvpUGDBixbtszKYsUivleM6bl6YDNc7uq6oK4uERFxUZYGnz59+vDNN9+wZs0a7rnnHux2O2AGonvuuYfg4GCWL19O3bp1rSxWLHJli08FtfiIiIgbsnw6+9ChQ/noo4/48ccfGTNmTHboCQoKYtmyZQQEBFhdpFjk6jE+V9MYHxERcXUlMp390UcfJS4ujpdffplp06Zld2/Vq1evJIoTi1xvjI9mdYmIiKsrVvA5cuRIvsdGjRpFdHQ0v//+O9OnT8cwjBznBwUFFadoKQFVrhzj4537ePYYH7X4iIiIiypW8GnQoAG2q+c8X8UwDPr06ZPjNZvNRkaGvj2dzXVbfNTVJSIiLq5YwWfEiBHXDT7iOq43xsdHXV0iIuLiihV8pk+fblE1xBlcd3CzZnWJiIiLs3xWl7iuKurqEhERN1es4GMYxvVPKoVriDVytPhcY3BzmoKPiIi4qGIFnzZt2vD9998X6b1Hjx7l0Ucf5e233y5OFcRCfprOLiIibq5Ywadp06bcc889NGrUiBdffJFt27ZdswXn1KlTzJw5kwEDBtCkSRPmz59Pp06dilMFp7VgwQKaN29O06ZN+eKLLxxdnQK5cjp7nnt1qatLRERcnM0oZl/TihUrmDBhAqtWrcJms1GpUiXat2+Pv78/VatW5cKFC5w+fZo9e/Zw6NAhAKpVq8b/+3//j6effprKlStb8oM4k4yMDFq1asWyZcvw8/OjY8eOrFmzhho1auT7nqSkJPz8/EhMTMTX17cUa3tZhh0af2g+njoI+l61l+yxJOg+zZzdtWds6ddPREQkL4X5Di32ys29e/dm5cqV7Nixg2nTprF06VLWrFmTvU9Xlho1anD77bczZMgQ7r77bsqXL5/PFV3fhg0baN26NYGBgQBERESwePFi7rvvPgfX7Nq8PMzZXCkXr7NJaQbYDfDQSgYiIuJiLJvV1bp1a9599122bNlCYmIie/bsYc2aNWzdupVjx45x8uRJ5syZwwMPPFDk0PPJJ5/Qrl07fH198fX1pVu3bixcuNCqHwGAlStXMnDgQAICArDZbMybNy/P8yZPnkyDBg3w8fGhS5cubNiwIftYbGxsdugBCAwMJCYmxtJ6lhT/SuZ9zYq5j125cakGOIuIiCsqkenslSpVomnTpnTt2pWQkBDLNiatV68eb731Fps3b2bTpk2Eh4dz++23s2PHjjzPX716NRcv5h6Ju3PnTuLi4vJ8T0pKCiEhIUyePDnfesyaNYvIyEhefPFFtmzZQkhICP379yc+Pr5oP5gT+W9/+O/N0KR67mM+V7QPapyPiIi4Ipdax2fgwIHceuutNG3alGbNmvH6669TuXJl1q1bl+tcu93O2LFjGTZsGJmZmdmv79mzh/DwcL788ss8y4iIiOC1115jyJAh+dbj/fff5+GHH2bUqFG0atWKTz/9lIoVKzJ16lQAAgICcrTwxMTEuMyu9O3rwB0t8z7mYYPynuZjzewSERFX5FLB50qZmZnMnDmTlJQUunXrluu4h4cHv/zyC1u3bmXEiBHY7XYOHDhAeHg4gwcP5umnny5Suenp6WzevJl+/frlKKtfv36sXbsWgNDQULZv305MTAzJycksXLiQ/v3753m9yZMn06pVKzp37lyk+pQ2LWIoIiKurNiDm0vbtm3b6NatGxcuXKBy5crMnTuXVq1a5XluQEAAS5cupWfPngwbNoy1a9fSr18/PvnkkyKXn5CQQGZmJv7+/jle9/f3Z/fu3QB4eXnx3nvvERYWht1u5+mnn853RtfYsWMZO3Zs9oh0Z1fBC86i4CMiIq7J5YJP8+bNiY6OJjExkdmzZzNy5EhWrFiRb/gJCgri66+/pnfv3jRq1IgpU6aUysaqgwYNYtCgQSVeTmnLntmlri4REXFBLtfV5e3tTZMmTejYsSNvvvkmISEhTJw4Md/z4+LiGDNmDAMHDiQ1NZXx48cXq/yaNWvi6emZa3B0XFwcderUKda1XYEWMRQREVfmcsHnana7nbS0tDyPJSQk0LdvX1q2bMmcOXOIiopi1qxZ/OMf/yhyed7e3nTs2JGoqKgcdYiKispzrJG78dEO7SIi4sIs7eoKDw+ne/fuvPrqq1ZeNttzzz1HREQEQUFBnDt3jm+//Zbly5ezaNGiXOfa7XYiIiIIDg5m1qxZeHl50apVK5YsWUJ4eDiBgYF5tv4kJyezf//+7OeHDh0iOjqa6tWrExQUBEBkZCQjR46kU6dOhIaG8sEHH5CSksKoUaNK5Od2JtqvS0REXJmlwWf9+vV07drVykvmEB8fz4gRIzh+/Dh+fn60a9eORYsWcdNNN+U618PDgzfeeIOePXvi7X15E6qQkBB+++03atWqlWcZmzZtIiwsLPt5ZGQkACNHjmT69OkA3HPPPZw8eZIXXniBEydO0L59e3799ddcA57dUQW1+IiIiAsr9l5dV+rYsSMtWrRgxowZVl2yzHCGvboKYtxC+GkvvNQbRrV3dG1EREQK9x1q6Rifxx9/nPnz57Nz504rLytOxEddXSIi4sIs7epq1KgRffr0oWvXrjzyyCN07twZf3//PKeP9+rVy8qipZSoq0tERFyZpcGnT58+2Gw2DMPgvffeu+Z6OVduIyGuQys3i4iIK7M0+LzwwgulsjigOI5mdYmIiCuzNPi89NJLVl5OnFD2ys1q8RERERfk8gsYSunKWrlZwUdERFxRiezVlZKSwrx584iOjiYpKQlfX1/at2/P4MGDqVSpUkkUKaVEg5tFRMSVWR58fvjhB8aMGcPZs2e5cokgm81G1apV+fzzz7njjjusLlZKSeVLa0GeveDYeoiIiBSFpcFnzZo13HvvvXh6evLQQw8RFhZG3bp1OXHiBMuWLePLL7/k3nvvZcWKFWViXyt31KCqeX/orCNrISIiUjSWrtw8YMAAli9fzurVqwkJCcl1/M8//+TGG28kLCyMn376yapi3YKrrNx8/iK0+Nh8vHUMVK/g2PqIiIg4bOXmtWvXcs899+QZegDatWvH3XffzZo1a6wsVkpRhXJQr4r5+MBpx9ZFRESksCwNPqmpqdfdqNPf35/U1FQri5VS1ri6eb//jGPrISIiUliWBp8GDRqwZMmSa54TFRVFgwYNrCxWSlmTaub9frX4iIiIi7E0+Nx9991s3ryZkSNHEhsbm+PY8ePH+dvf/sbmzZu55557rCxWSllWi88BtfiIiIiLsXRwc2pqKmFhYWzcuBFvb2+aNGmCv78/cXFx7N+/n/T0dEJDQ1m2bBkVKmhU7JVcZXAzwLpjcM8PEOQHv//N0bUREZGyzmGDmytWrMjKlSt56aWXqFevHjt37mTZsmXs3LmTevXq8fLLL7NixQqFHhfX+FJX19FEreAsIiKuxdIWn6udO3cue+XmKlWqlFQxbsGVWnwMA0I+g8Q0+HUYtKzl6BqJiEhZ5rAWH09PT4YPH579vEqVKgQGBir0uBmbTeN8RETENVkafHx9falfv76VlxQnldXdpeAjIiKuxNLgExoayh9//GHlJcVJaUq7iIi4IkuDz0svvcTSpUv56quvrLysOKEmWsRQRERckKWblC5ZsoQ+ffowatQoPvzwQzp37oy/vz82my3HeTabjQkTJlhZtJSyrK6ug2fAboCH7drni4iIOANLZ3V5eBSsAclms5GZmWlVsW7BlWZ1AWTYocVkuGiH1aOgnvNXWURE3FRhvkMtbfFZtmyZlZcTJ+blAQ2qwr7T5jgfBR8REXEFlgYfm82Gr68v7du3t/Ky4qSaVDeDz4Ez0KeBo2sjIiJyfZYObg4LC+P//u//rLykOLHsKe2a2SUiIi7C0uBTu3ZtfHx8rLykOLHGmtklIiIuxtLgc9NNN7F8+XJKcBcMcSJN1OIjIiIuxtLg89Zbb3Hq1CnGjBnD6dP6NnR3WV1dCefh7AXH1kVERKQgLB3cfP/991O1alWmTp3KN998Q8OGDfNdxycqKsrKosUBKnlD3cpwPNkc4NyxrqNrJCIicm2WBp/ly5dnP05LS2P37t3s3r0713lXByFxXY2rmcFn/2kFHxERcX6WdnXZ7fYC3bR4ofvQLu0iIuJKLA0+UvZogLOIiLiSUg8+6enpJCUllXaxUkKyp7Qr+IiIiAsodvBp1KgRkyZNyvHaokWLiIyMzPP8N998k2rVqhW3WHESWTO7jiTBRfVgioiIkyt28Dl8+DBnz57N8dq6deuYOHFicS8tLqB2JfD2NHdoP5Hi6NqIiIhcm8b4SLF42KBOZfPx8XOOrYuIiMj1KPhIsQVUMe9jFXxERMTJKfhIsQVcavFR8BEREWen4CPFlt3ik+zYeoiIiFyPgo8Um7q6RETEVViyZcU333zDunXrsp/v378fgFtvvTXXuVnHxH1kBR8NbhYREWdnSfDZv39/noHm119/zfN87dXlXrLG+MQo+IiIiJMrdvA5dOiQFfUQF1b3UotPYhqkpJu7touIiDijYgef4OBgK+ohLsy3PFTxhnPp5gDnptUdXSMREZG8aXCzWKKuxvmIiIgLUPARS2gtHxERcQUKPmIJTWkXERFXoOAjltAihiIi4goUfMQSavERERFXoOAjltAihiIi4goUfMQSVy5iaBiOrYuIiEh+LFm5OS8pKSmcPXuWzMzMPI8HBQWVVNHiAHUuBZ+0TDhzAapXcGx9RERE8mJ58JkyZQrvvfcee/bsyfccm81GRkaG1UWLA5X3gloV4WSq2eqj4CMiIs7I0uDzySefMHbsWLy8vOjVqxf16tXDy6vEGpXEyQRUMYPP8XPQtrajayMiIpKbpankgw8+oGbNmqxatYpmzZpZeWlxAXUrwx9x2qxUREScl6WDm//66y/uvvtuhZ4yKntml9byERERJ2Vp8Klbt26+g5nF/WlKu4iIODtLg8/IkSNZuHAhKSkpVl5WXERW8FFXl4iIOCtLg8+///1vOnfuzE033cTKlStJTlafR1miFh8REXF2lg5uLl++PACGYRAWFpbveZrO7p6yFjE8kQIZdvDS8pgiIuJkLA0+PXv2xGazWXlJcSG1KkE5D7hoh/iUyy1AIiIizsLS4LN8+XIrLycuxsMG/pXhWJI5zkfBR0REnI06I8RSgRrnIyIiTqzEllWOiYkhOjqapKQkfH19ad++PYGBgSVVnDiJupfG+cQq+IiIiBOyPPjs37+fxx57jKVLl+Y61rdvXz7++GOaNGlidbHiJLJafGI1oU9ERJyQpcHn6NGj9OjRg/j4eFq0aEGvXr2oW7cuJ06cYOXKlfz222/07NmTDRs2UL9+fSuLFidRNyv4qMVHRESckKXB5+WXXyY+Pp6PP/6YRx55JNcMr88++4zHHnuMV155hc8//9zKosVJBCj4iIiIE7M0+CxatIiBAwfy6KOP5nn8kUce4ZdffmHhwoVWFitOJGstH+3XJSIizsjSWV3x8fG0adPmmue0adOGkydPWlmsOJEAX/P+9Hk4f9GxdREREbmapcGnVq1a7Ny585rn7Ny5k1q1allZrDgRX2+oVM58rFYfERFxNpYGn/79+/Pjjz8yZcqUPI9PnTqVn376iVtuucXKYsWJ2GyXx/kcSXRsXURERK5mMwzDsOpiR44coVOnTpw6dYpWrVrRu3dv/P39iYuLY+XKlezYsYOaNWuyadMmzeq6SlJSEn5+fiQmJuLr6+vo6hTLE7/CvD3wZBcY39XRtREREXdXmO9QSwc3BwUFsXr1ah555BGWL1/Ojh07chwPCwvjk08+Uehxc50DzOCzMdbRNREREcnJ8gUMmzZtytKlSzl69GiulZvLUuBZsGABTz31FHa7nWeeeYaHHnrI0VUqNZ0DzPutJ+BiJpTzdGx9REREspTYlhX169cvU0HnShkZGURGRrJs2TL8/Pzo2LEjQ4YMoUaNGo6uWqloWgN8y0NSGuxKgHb+jq6RiIiISZuUloANGzbQunVrAgMDqVy5MhERESxevNjR1So1HjboVNd8rO4uERFxJsVq8Rk9ejQ2m4033ngDf39/Ro8eXaD32Wy2fGd+Xcubb77JnDlz2L17NxUqVODGG2/k7bffpnnz5oW+Vn5WrlzJO++8w+bNmzl+/Dhz585l8ODBuc6bPHky77zzDidOnCAkJIQPP/yQ0NBQAGJjY3NsyBoYGEhMTIxldXQFnQNg6WEz+DzYwdG1ERERMRUr+EyfPh2bzcYzzzyDv78/06dPL9D7ihp8VqxYwdixY+ncuTMZGRk8//zz3HzzzezcuZNKlSrlOn/16tWEhoZSrly5HK/v3LmTGjVq4O+fuw8mJSWFkJAQRo8ezR133JFnPWbNmkVkZCSffvopXbp04YMPPqB///7s2bOH2rVrF/rnckdZ43w2xYJhmNPcRUREHK1YwefQoUMA2a0bWc9Lyq+//prj+fTp06lduzabN2+mV69eOY7Z7XbGjh1L06ZNmTlzJp6e5gjbPXv2EB4eTmRkJE8//XSuMiIiIoiIiLhmPd5//30efvhhRo0aBcCnn37Kzz//zNSpU3n22WcJCAjI0cITExOT3RpUVrT1B29POJkKfyVCg6qOrpGIiEgxg09wcPA1n5e0xERzhbzq1avnOubh4cEvv/xCr169GDFiBF9//TWHDh0iPDycwYMH5xl6CiI9PZ3Nmzfz3HPP5SirX79+rF27FoDQ0FC2b99OTEwMfn5+LFy4kAkTJuR5vcmTJzN58mQyMzOLVB9n5eMF7WrDpuOwIUbBR0REnIOlg5tfeeUVVq5cec1zfv/9d1555ZVil2W323nyySfp3r17vvuDBQQEsHTpUlatWsWwYcMIDw+nX79+fPLJJ0UuNyEhgczMzFzdZP7+/pw4cQIALy8v3nvvPcLCwmjfvj1PPfVUvjO6xo4dy86dO9m4cWOR6+SsQi8Nc9IAZxERcRaWBp+XXnqJ5cuXX/OclStX8vLLLxe7rLFjx7J9+3Zmzpx5zfOCgoL4+uuvmTVrFl5eXkyZMgVbKQw4GTRoEHv37mX//v2MGTOmxMtzRp2uGOcjIiLiDEp9Ont6enr2eJuiGjduHAsWLGDZsmXUq1fvmufGxcUxZswYBg4cSGpqKuPHjy9W2TVr1sTT05O4uLhc5dSpU6dY13Y3WVPaD56FhFSHVkVERAQogeBzrdaU9PR0fv/99yLPfDIMg3HjxjF37lyWLl1Kw4YNr3l+QkICffv2pWXLlsyZM4eoqChmzZrFP/7xjyKVD+Dt7U3Hjh2JiorKfs1utxMVFUW3bt2KfF135OcDzS/18KnVR0REnEGxV25u1KhRjuf//e9/mTZtWq7zMjMzSUhI4MKFCzz88MNFKmvs2LF8++23zJ8/nypVqmSPqfHz86NChQo5zrXb7URERBAcHJzdzdWqVSuWLFlCeHg4gYGBebb+JCcns3///uznhw4dIjo6murVqxMUFARAZGQkI0eOpFOnToSGhvLBBx+QkpKSPctLLuscAHtOmeN8bmni6NqIiEhZV+zd2Rs0aJDdynPkyBF8fX2pWrVqrvM8PT2pXr064eHhTJgwIc91d65b2Xxak6ZNm8bf/va3XK8vWbKEnj174uPjk+P1rVu3UqtWrTy7yZYvX05YWFiu10eOHJljnaKPPvooewHD9u3bM2nSJLp06VK4H+gK7rQ7+5Xm7oYnF0F7f5h/r6NrIyIi7qgw36HFDj5X8vDw4KWXXuKFF16w6pJlhrsGn2NJ0H0aeHnAtkehYrnrv0dERKQwCvMdaukmpYcOHcqztUfKrsAqULcyHE82d2vvXjb3rRURESdh6eDm4OBg/Pz8rLykuDibLef2FSIiIo5kaYtPlrVr1/Lbb78RGxtLWlparuNF3atLXFOHOvDjXtgW7+iaiIhIWWdp8MnIyOC+++5jzpw5GIaBzWbjyiFEWc8VfMqWNpdWL9iu4CMiIg5maVfXe++9xw8//MCoUaPYtGkThmHw5JNPsnbtWt5++22qVq3KXXfdxYEDB6wsVpxcy5rm/fFkOKWFDEVExIEsDT4zZsygTZs2fPHFF9xwww0AVK1alS5duvDPf/6TlStXsmDBAhYtWmRlseLkqpSHhlXNxztOOrQqIiJSxlkafPbv30+fPn2yn9tsNi5evJj9vHXr1gwcOLBYm4SKa1J3l4iIOANLg4+3tzcVK1bMfl65cmXi43N+0wUHB7Nv3z4rixUX0KaWeb9dLT4iIuJAlgaf+vXrc/To0eznLVq0YOXKlTkGOK9bt47q1atbWay4gNaXgs8OtfiIiIgDWRp8evfunSPo3HPPPezZs4cBAwYwefJk7rvvPlatWsUtt9xiZbHiAlpf6uo6nAhJuVc4EBERKRWWTmcfPXo0mZmZxMTEUK9ePR5//HGWL1/OggULWLhwIQChoaG89dZbVhYrLqB6BXMV55hzsPMkdM29TZqIiEiJszT43HDDDTkGLpcrV44ff/yRTZs2ceDAAYKDgwkNDcXDw9KGJnERbWqbwWd7vIKPiIg4Roms3Hy1Tp060alTp9IoSpxY61qw6ICmtIuIiOOo6UVKjWZ2iYiIoxWrxSc8PLxI77PZbERFRRWnaHFBWWv57D8N5y9ChXKOrY+IiJQ9xQo+y5cvz/P1q/fouvp1m81WnGLFRdWuBLUqwslU2H3K3LxURESkNBWrq8tut+e4nT9/ngEDBtCsWTO+/vprDh8+zPnz5zl8+DBfffUVzZo1Y+DAgaSmasOmsshmg1ZZ3V1az0dERBzA0jE+L774Itu2bWPjxo0MHz6coKAgypcvT1BQEPfffz/r16/njz/+4MUXX7SyWHEh2rpCREQcydLg8+233zJ06FAqV66c53FfX1+GDh3K//73PyuLFReiAc4iIuJIlgafkydP5tiUNC8ZGRm59u+SsiOrxWfvKUjPdGxdRESk7LE0+DRu3Jjvv/+eU6dO5Xn85MmTfPfddzRp0sTKYsWF1PcF3/Jm6Nl32tG1ERGRssbS4PPkk09y4sQJbrjhBiZOnMjmzZs5evQomzdv5oMPPqBjx47Ex8czfvx4K4sVF2KzXd6wVON8RESktFm6cvNDDz3E8ePHefXVV4mMjMxxzDAMPD09eemllxg9erSVxYqLaVMb1h4zg889rR1dGxERKUss37JiwoQJDBs2jBkzZvDnn3+SmJiIn58fISEhDBs2jMaNG1tdpLiYrAHO0SccWw8RESl7SmSvrsaNG/PCCy+UxKXFDXSrDx42+DMeDp6BRtUcXSMRESkrtFeXlDr/StA72Hw8e6dj6yIiImVLsVp8Vq5cCUBoaCg+Pj7ZzwuiV69exSlaXNzdrWDZYZi9C57qBp6K4CIiUgqKFXz69OmDzWZj165dNGvWLPt5QWRmahGXsqxfI6jmA3EpsPIIhDVwdI1ERKQsKFbweeGFF7DZbNSsWTPHc5Hr8faEIS1gajR8t0PBR0RESofNyGsbdSl1SUlJ+Pn5kZiYiK+vr6OrUyp2noSIb6GcB2x4CKpXcHSNRETEFRXmO1QjK8RhWtUy1/S5aIf5exxdGxERKQsUfMSh7mpl3n+n2V0iIlIKijXGJzw8vEjvs9lsREVFFadocRODm8Prv5vdXtvjL29iKiIiUhKKFXyWL19epPdpALRkqeoDNzeCBfvg+50KPiIiUrKK1dVlt9uLdNNUdrnS3Zf265q729y1XUREpKRojI84XI/64FseEtNg32lH10ZERNyZgo84nKcHtKhhPt6T4Ni6iIiIeyuRTUovXLjAxo0biY2NJS0tLc9zRowYURJFi4tqXhM2xMLuU46uiYiIuDPLg8/kyZOZMGECiYmJeR43DAObzabgIzlktfjsVouPiIiUIEu7uubMmcPjjz9O/fr1effddzEMg9tvv5033niDW265BcMwGDp0KFOnTrWyWHEDzc1dT9ijFh8RESlBlgafDz74gNq1a7N27VrGjx8PQPv27XnmmWf4+eef+eabb5g3bx7BwcFWFituoPmlFp8TyZB4wbF1ERER92Vp8Pnzzz8ZNGgQFStWzH7tyqnrw4YNIzw8nFdeecXKYsUN+JaHelXMxxrnIyIiJcXS4HPx4kVq1aqV/bxChQqcPXs2xzkhISFs2bLFymLFTWR1d+3SOB8RESkhlgafgIAAjh8/nv08ODiYrVu35jjnr7/+wsurRCaTiYvTlHYRESlplgafzp0752jNueWWW1i9ejVvvvkmO3bs4LPPPmPOnDl07tzZymLFTWS1+KirS0RESoqlweeuu+4iLS2Nw4cPA/Dcc89Rr149/v3vf9OuXTsee+wxKleuzH/+8x8rixU3kdXis/cUGIZj6yIiIu7JZhjF+4qZOXMmd9xxB97e3nkeP3PmDF988QUHDx4kODiYBx54gMDAwOIU6ZaSkpLw8/MjMTERX19fR1fHIS5mQsuP4aIdVo2C+mXzYxARkUIqzHdosYOPh4cH1atXZ/jw4YwePZqQkJDiXK7MUvAx9f/G7OqaMhD6NXJ0bURExBUU5ju02F1d9913H+fPn+fDDz/khhtuoHPnznz66af5rtwsci0tssb5aICziIiUgGIHnxkzZnD8+HEmT57MDTfcwObNmxk7diwBAQE88MADLF++3IJqSlnRQis4i4hICbJkcLOvry+PPfYYGzduZNu2bTzxxBNUrlyZGTNm0LdvX5o0acIbb7xBTEyMFcWJG8tawVlr+YiISEmwdFYXQOvWrXn//feJiYlh9uzZRERE8Ndff/Hvf/+bBg0acNtttzFnzhyrixU3kdXic/AMpGU4ti4iIuJ+ij24uSBOnDjBV199xdSpU9m7dy8eHh5kZOhb7Uoa3GwyDGj3KSSlw8Jh0KrW9d8jIiJlW6kObi6IM2fOEB8fn719RSlkLXFRNpsWMhQRkZJTYntHJCcn87///Y+pU6eyYcMGDMOgYsWKjBgxggcffLCkihU30LwGbIzV1hUiImI9y4PPihUrmDp1Kj/88APnz5/HMAw6d+7Mgw8+yH333UeVKlWsLlLcjKa0i4hISbEk+MTExDB9+nSmT5/OwYMHMQyDGjVq8PDDD/Pggw/Spk0bK4qRMkJT2kVEpKQUO/hERETw22+/kZmZic1mo1+/fjz44IMMHjw4320sRK4la0r78WRIvAB+Po6tj4iIuI9iB59FixYRFBTEqFGjGDVqFEFBQVbUS8ow3/IQWAVizpkDnLtoazcREbGIJcGnX79+2Gw2K+ojAkDb2mbwWbRfwUdERKxT7OnsN910k0KPWG5YW/N+1k44l+bYuoiIiPsolXV8RAqrVxA0qQ7J6TBrh6NrIyIi7kLBR5ySzQYPtjcfT/sDMu0OrY6IiLgJBR9xWne0hGo+cCwJFh90dG1ERMQdKPiI0/LxujzWZ8pWx9ZFRETcQ4ltWSFihZHt4LPN5hYWf8ZBO//8zz19HnYlQFKaOSA66dKg6FubQoAWDBeRMmR3Ajy8AIa3gUc7Obo2zsXS4DNr1izuuOMOypUrZ+VlpQzzrwwDmsK8PWarz8Rbcp+zPR6mRcOPeyE9M/fxN1fDwGYw5gbt9i4iZcMnm+BIovn7r3oFuLu1o2vkPGyGhVule3h4ULNmTUaMGMFDDz1EixYtrLq020tKSsLPz4/ExER8fX0dXR2nsi0OBswELw+YfRcYBpy9AHEpMGcXbIi9fG6wH9SsCFW8zYUQTyTnPN4zCJ7voQAkIu7r7AUI/QLSLv0h6OUBX94OPdx4feHCfIdaGnxeeOEFpk+fzrFjx7DZbHTv3p2HH36Yu+66Cx8f7TtwLQo+13bn92Z3V168PODWJjC6A3Sok/v4n3Hwf1vg531gN6CyN0wbBKFaGFFE3NDUrfDySmhVE5rWgPl7zD8Gf7gLmtd0dO1KhsOCD4DdbmfhwoV88cUX/Pzzz2RmZuLr68v999/PQw89REhIiJXFuQ0Fn2tbcxQe/Ak8bFDVx7xV8zGDzvC2UKfy9a9xNAn+sQTWHTMHTv/fAOgdXPJ1FxEpLYYBN8+Avafg1T5wT2u4f67Z8h1YBebeA/6VHF1L6zk0+FwpPj6eadOmMWXKFPbv34/NZqNjx46MGTOGe++9l8qVC/BtVUYo+FyfYZjr+xTHhQx49GdYdhi8PeHDW+CWJpZUT0TE4TYfhzu+M/+42/iQ2eV/5jwM+Q4OnQUbUMkbKpaDSuWgWgVoUQNa1DRbiFrUhCrlHf1TFJ7TBJ8rLVmyhFGjRnH8+HEAKlWqxP33388zzzxDcLD+7FbwKT3pmfDEr/DLfvC0wXs3wxANRxMRN/CPJfD9Trizpfm7Lcvhs2bLz9Gk61+jcTWzNb1DHehQF1rWNFvbnZlTBZ+dO3fy+eef880333Dq1CkqVarEkCFDiI6OZvv27VSoUIHZs2cTERFRktVwego+pSvDDs/8BrN3meHn2zugaz1H10pEpOiS0qDzF2bL9uy7oHNAzuMZdnPZj9SLkHIRUtPheLI59X3Xpdvx5NzXbeBnjqG8q5XZUuSMHB58zp8/z8yZM/n8889Zv349hmHQrl07HnnkEe6//36qVDEXVVm4cCF/+9vf8Pf3588//7S6Gi5Fwaf02Q2z5efHvVCjAvx0LwTqoxcRF/X1n/DvZdC0Oiy5v2hDA06lQnQcbD0BW4+b9ykXzWN+5c0xlSPaQV0nWxvNYcFn06ZNfPHFF8ycOZNz587h4+PD3XffzaOPPkqXLl3yfM/zzz/Pu+++S3p6ulXVcEkKPo5x/iLc8T3sPAlta5t/JfloWU8Rycfp8+bvjYAqxR9zaLVbv4UdJ+GFXvBgB2uumXrR7DqbshX+SjRf87BB9/pwRwvo39gcM+RohfkOtfRXfGhoKACtWrXikUceYcSIEfj5+V3zPUFBQQQGal6xOEaFcubsroH/g23x8PxSeO8m5/uFVhDfbjOn/L/ZV+FNpCScTIG+X0NiGtSqaI6BaX9pLEyIv2MDwJbjZujx9jQDiVUqloORIXB/W/jtkBmA1sfA70fMW8VyMKgZTOhlLhXiCixt8XnggQd45JFH6NGjh1WXLDPU4uNYq4/CA3Mh04CXesOo9o6uUeF1+hxOpsJHEeZK1SJirffWwqQNeR/zsEHzGpfDUKNqEOQLtSpdHhhsGGa3UUIqnDoPiRfgbJp5n5ZhzqbyvXSr4g3lPMHLBp4e5u30eYg9d/kWk3WfBEmXOk0GNYMPS3jI7F9nYe5umLP7civQoGYw6RbH/dHo8DE+UngKPo73xRZ49XdzsPPMoa61wGFaBjSbbD4e2hLev/na54tI4Zy/CF2nmqsi//dmqO8H0SfMMTDRJ8wQkpfynlDP15xNmpAK5zNKro51K8OUQdC6lFamNwxYehjGLDAHTr8WBg+0K52yr+awri4RV/ZgB/gz3lzldNxC+GWYuf2FKzhxxUyMFYfNgdvOPv1UxJV8t9MMPfV94fbmZgvMlbOm4pIvDQg+Ya4WfyTJbI1Jy4QDZ3Jeq1I5c/8sPx+oWt689/GC5HSzGy1ro+UMu3nLNCAj0zwvoMoVt8rmhIzAKuattLvabDbo2xCe7Q6v/Q6vrIT2/tD2GptJOwNLg0+jRo2ue46Hhwe+vr40b96cIUOGcPfdd1tZBZEis9ngzXCzn3z/afj7r/D1YPMXnLOLvSL4JJyHHfHO/8tHxFVk2uGLrebjh27I+3eCf2VzMdQrF0S9mGmGn6NJZrCpXcn8Y8pZp4QX1UMdYEMMLD4Ij/0CPw8zZ4A5K0t/pdvtdtLT0zl8+DCHDx/m2LFjXLhwgWPHjmW/duHCBfbv38+sWbO47777uPnmm8v8jC5xHpW84ZNboYKXOe5n4npH16hgjl/VzL7sL8fUQ8QdLTpg7nRe1QfublXw95XzhOCq5uagnQIgyM/9Qg+YfzS+e5PZGnY0Cf65xOwGc1aWBp/o6Gjq1q1LeHg4a9asIS0tjdjYWNLS0lizZg19+/YlICCAI0eOsHfvXm699VaioqJ47733rKyGSLE0q2HOjAJzIONKFwgRsZeCT9ZsruWHHVYVEbdiGOYmx2COX3HH4GIFPx/4+FZzVtmiA2bXoLOyNPg888wzpKWlsXjxYrp27Yrt0vBum81G165d+fXXX7lw4QLPPvssTZo04fvvvyc4OJiZM2daWQ2RYhvSAoa3AQN4YlHuFhVnk7Xa6sCm5v3WE+Z4BBEpnk2x5v9P5T1hpIMG7rqKdv7wWEfz8bLDDq3KNVkafObPn8+tt96Kh0fel/X09OTWW29l/vz5APj4+BAeHs7+/futrIaIJV7oDW1qm1NIP9/i6NpcW1aLT8cAs8XKbrhGS5WIs8tq7bmjpTk1Xa4ta8D3ngTH1uNaLA0+SUlJJCVdewe0xMREEhMTs5/XrFnTyiqIWMbHCx7vbD5eetihVbmurOBTtzL0ubTn73IFH5FCsRvmWJ7fDsLHG+HJRbDkoHnsIYtWQnZ3zS99pR9ONPcMc0aWzupq1aoV//vf//jHP/6R5wyvgwcPMnPmTFq1ujw67MiRI9SqVUqLDogUUo8gKOcBh87CoTPQsJqja5S3rFldAVWgTwPzr1RNaxfJm2GYfyzsOQV7T8He0+b9/tN5r7NzS2NoUr306+mKalU0p+qfPg/7Tjnn7FJLg8/zzz/PnXfeSfv27XnooYfo3r07tWvXJj4+ntWrVzNlyhSSk5N5/vnnAUhPT2fx4sXcfLNWWxPnVNnbXMhw9VGzz9oZg09KurnuB5gtPg2qmuuEaFq7iLkezpW7j+++FHaS85lM7O0JjauZG302q2GuxtwzqHTr7Mpsl1awXnvM/Kyd8fePpcHnjjvu4IsvvuDJJ5/kgw8+YOLEidnHDMOgcuXKfPbZZ9xxxx0ApKamMmXKFFq3bm1lNUQsFdbADD5LD8NoJ2zuzmrtqeJtLnkPZkvVogPmtHZn/MUjUhJOn4ft8ea+e9vjYftJs+sqL14eZsBpVuNyyGlWA4L9zGNSdNnBx0nH+Vi+cvPo0aMZOnQo8+fP548//iApKQlfX19CQkK4/fbbc2xaWrVqVW6//XarqyBiqfCG5qqk62PM1hVn2In4SlkzzgKqXH6tT/Cl4HMY/h7qkGqJlKgLGWbAiT4Bf8SZM6+O5TPEtE5laFkTWtWEFpduDaqarTtivRaXxvnsPeXYeuTH0uDzyiuv0LBhQx544AFGjBhh5aVFHKZRVXPhsSOJZsvPzY0dXaOcrhzYnKVPA/M++tK09qo+pV4tEUudS4PNx80VgtfHmNvLpGfmPq9RVXM2Zpva5p5VrWtBtQqlXt0yrXkN8353WQg+r732Gk8++aSVlxRxOJsNwhvA9D/M7i5nCz7HrxjYnCWgivnLZ88pWPGXubeQiKtJSjNnVS3YC78fgYv2nMdrVby8G3qIv7mOjK8Tb5VQVjS7FHziU+DMeecLnpYGn6CgIM6ePWvlJUWcQlgDM/gsO2zOCLE50Uyp7BafKjlfv6mRGXxmbFPwEdeyMRY+22yG9itbder7QtdAc8JBl0CzJdaZ/l8UU2Xvy9tX7D4F3eo5ukY5WRp87r33Xr766isSExNzjOURcXVd65nr+pxINmeGtHKiFRiygk9A5ZyvP9DO/PJYH2N2ebWvU/p1EymM/afhP2vM8WlZmlQ3VyS/tenllgRxfs1rXAo+Cc4XfCwduz5hwgTatWtHeHg4P//8M/Hx8VZeXsRhfLyge33zsbMtxZ7V1XV1i0+dypdbej7bXLp1EimM0+fhX0vh5m/M0ONhg/vawOLh8Nv98GRXhR5X09yJBzhb2uJTsWJFwJy6PmjQoHzPs9lsZGQ46ZKOIvkIbwBRh2DpIRjb2dG1MWUtxAa5W3wAxtwAs3fBrwfgr7PmTtEizsRuwMh55mBlMLton+luTjEX19XCiQc4Wxp8evbsmb0xqYi7CWtg3m9xoplSiWmXV5q9usUHzL+6+gSb21d8vhVeCyvd+olcz497zNBTxRumDDLH7ojru3JKu7ONi7Q0+CxfvtzKy4k4lUBf55spldXaU6OC2R2Xl0c6msHn+50wvgvUqFh69cuSetFcM0ULw8mV0jLgnbXm40c7KvS4k4ZVze1+ktPh2DlzsLOzsHwBQxF3FtbADD6zdsDNjaBCOcfW53g+M7qu1K0etKtt/lX91Z8wvmvp1A3g8Fl4by38uNcct1GrojnVPmtrjabVoWkNaFLN8Z9lQdkN8157oBXft9vNRQdrV3LOVdGl6Mp5mgPTdyWYO7W7ffBJT0/nt99+Y/fu3aSkpDBhwgQALly4QFJSEjVr1sTDQ3/6iesZ2MzcAHT1UbjtfzCxv2O3hMjenDSP8T1ZbDaz1WfsQvjyD/Mv65IOGXHJMGkDzNwBGZfWXrEbEJdi3rZeXUegnq85PTnID4J8zTBXzuPyzwBQwcvsEqnkbU6ZrVGhdFfSjj0Hg2aa68l0q2cOeO9R3wxxztSU7wrOpZn/jYDZElnRRYKvFFyzGpeCzynol3vfcoexPPj8+OOPjBkzhpMnT2IYBjabLTv4/Pnnn3Tr1o2vv/6aYcOGWV20SIlrUxu+uh2eWgIHzsDg78xf2o91Ak8HZPmCtPgA3NLk8roa3++EESFFK89uwEcbzUXi7m2du3stMQ0+2wRTos0tBcBsJftHN/Ov+uPnzFlosefMz2//aXNn7NPnzbodTTJDZWFU8zFDU2AVc/B2m1rQtrb52OpWmUkb4GSq+XjhfvMG5mrBYzvD4Bbqziuo/9ti/rs3qgp3a7tGt9SiBszH+fbsshmGYVh1sdWrVxMWFkbdunX55z//ybp16/jf//5HZublFaiaN29OmzZt+OGHH6wq1i0kJSXh5+dHYmIivr5O1CYoeTpzHp5fCr9c+uLrVBc+uKX0m3Of+BXm7YHnusOjna597vQ/4MXlZt/70hFFCwUr/oIR88zHtSrC/+sEw9qaLTZf/wkfbjQHfgN0rGvOzinIuI2EVDh0Bo4kmVuDHEk0A5JhQNYvKLthDuROSTfHDZxLvxyu8lLFG1rXhm6B5qatIf5m83tR/XUWwr6CTAPe6msGoNVHYcvxy4vsNaoKT3QxWwYdEYRdRXwK9Jpu/nt+ehtENHF0jaQkRB2C0T+aYyMX31+yZRXmO9TSFp9XX32VqlWrsnnzZmrWrMmpU7nnsXXq1In169dbWaxIqatWAT6+FebshheWw6bjEDHDnDU1uEXp1SO/NXzycldLeHcNHDprLv/fO7jw5e08efnxyVR4eSV8shm8PcwBjGD26z9zozktuaDdPzUrmrfOhRzcmpQGMUkQc85sLdp/GnacNOt5Lh3WHTNv/11vdo11q2cuS3BzY7O8wpi4wQw9vYPNNWbA3AA2Jd0MfZ9uhoNn4YlFZqvYP280x4GpCyyn5HR4e7UZejrUgVucbAsYsU7WlPYDZ8w/DpxlU1hLg8/69eu58847qVmzZr7n1K9fn/nz51tZrIhD2GwwtCV0DjC/7LYcN++X/wWv9oEqpbBnUPYaPgUIPpW84a5WMDUapkcXLfjsutRkPb6L2XX10UYzdAD4V4LIrnBnq9Lr7vEtD761oOVVK2ln2M0QtPUErDpitsycuWDu+7TkIPxrmdkSdWsTsxuwdqVrl7PvNMzdbT5+6qrB4ZW8zda2+9vBtGizC2ffaRizwGz1eq6H+d9IWXUhwwyjq46Yty0nLo/7era7gqE7C6hitryeS4eDZy5PcXc0S4NPWlradZuYzp49q4HN4laC/OD7O+GjDWarwNzdsCkW3u53ebXnkmA3zC004NqDm680op0ZfJYdLtqChll99W39oW9DM+TM3W1OV7+3tfPMzPLyMH/Jtqhpts7YDfPLd+Vf5ricbfGw9ph5e2mFuZv9nS3NAZh5/VX6wTrzGjc3gpB8tv6o7A2Ph5rjpz7bDFO2mruJ3/m9+b6nupXuL/7zF80WyXPpkGk3w0amHapXNLs7G1Y1v5isDKlnL5gtivtOwR9x5m13Qu7NRYP8YGQ7cysYcV82mznAefNxc4CzWwafRo0asXHjxmues3btWlq0KMW+AJFS4OVhLqvfI8hs9TmaBMPmwD2t4V89wK8EFjtMSDW/UDxs4F/A4NOwmtnSs+Iv+Hob/LtnwctLzzSbrAFaXvoF5u1p/ozOzsNmDnhuW9schHwk0QxAv+yD6DhzLELUIXOg9OAWMLzt5ZWDd56EBfvMx5EFWArArzw8faP5xf7f9ebSB4sPmrebGsG4zqWzb9qrK2HG9mufU87DHBRet8rlZQb8K5mtWD5e5iw6Hy8z9KVnmv+9pWeaXYwJqXDqPJxKNVv9Dp81W9XyUr0ChAZAzyDzphXEy44WWcEnAXCCtc/A4uAzdOhQXnvtNaZNm8aoUaNyHX/33XfZvn07//nPf6wsVsRpdAqARcPNMQxf/Wl+6S09BK/0MTdZtFLWjK7alQr3V/vIEDP4zNphfpEXdBrxgdNmq4Gvt/kF6cqC/Mwp/o90NLvEZu+EH3abg26nRZu37vXNFrLvd5rvGdgsd5fatfhXNgdBP9gB/rvODFlZXW09g8xlBW6sXzLrAe09Bf/bcbneFbzM/0Y8bObPeOisGf7SMuFwonmzSp3KZmtS29pmwGvnD/WqqEurrMras8uZtq6wdFZXcnIyXbt2ZdeuXYSHh5OWlsbq1at56qmnWLt2LWvWrKF9+/asWbOG8uVLYQCEC9GsLvezMRae+e1yK0m72uY4kEHNrOkSWrgfHv3ZHCA6756Cv89uQO8vzS++t/peHqh7PXN2w/hF5l/u399VtDo7swy72RX2v+3w26HLCxWCGRiW3G8O3C6q/afhk01m12DmpWvX9zVbzO5qZQYGq4yaD0sPQ//G8H8D8j7Hbpjh+WiSuR5U1lID8SnmuJzzF80ByOczwMtmzojz9jTvfb3NFcBrVDAHideuZIadBlW1Ho/ktD4G7p5tdsevfbDkyinMd6ilwQfgzJkzjBs3ju+++y7HNHabzcbdd9/Nxx9/TLVq1aws0i0o+LinCxnmAODPNl+e8uzrDUNbQa8g88uuTmWzi6WwfxFP3WrOqrqtqTnDrDA+3wKv/W52WS0cVrCy31hl/hwj2sGrbr7n17EkmLHNDEFnLsDdreCdm6y59tEk8/Ofs8scfwNmsOoVZA60Dm9odjcV1aojMHyu2cKz5H5opF+34kDn0qDNp+bjLQ+X3JY5Dg0+WU6dOsXGjRs5ffo0vr6+dO7cGX9/By5x6+QUfNxbQqrZnTJju9nScjVvT/Ov/w514Ia65n3zGtdeC+bVlfDFVnioA0zoVbj6JF6ALlPMv+a/u7Nga+2MmGd2kb0Zbq7dUxZcyDAHQrcv5hpAeTl/0VwHauZ22BCb81jIpcHjN9Y3WwrLF3BQgt0wVxTfedLs0nylj7V1FimKsC/NpR6+vN2cSFASHLaOz5Vq1KjBLbfcUlKXF3EpNSuaU57HdDT/Iv9+J+w/A/HJkHD+8sDhA2dg9i7zPRXLmbMgWtWEVrXMW7val8NQ1ho+BZnKfjU/HxjSwtwr6cs/ChZ8smZ0NXeSmRmlwcer5KaiVyhnLocwtKX57/7zPog6aA62zpoR9f46KO8JHepClwDzPsTfHCycl7m7zdBTxRueCC2ZeosUVpvaZvDZFl9ywacwtEmpSCnysEGvYPOWJT3THFex95S5xsmW4xB9AlIumo+3HL98bog/vHuTOUW0MGv45GVkiBl8ft1v7p91re6V0+fNc8BsiRJrNa5mLob491Dzc156CJYfNseJnTp/eSHGLPV9zf8W2tY2B1y3rGmGnXfWmMfHdS65LgWRwmrnb25UvC3e0TUxWR58du7cyUcffcTGjRs5e/ZsjnE+WWw2GwcOHLC6aBGX5O1p7jVVz9cc3wHmeisHzpgLBu68tBLx5uNmK8Bt/zMXEMxaOLCga/hcrUVNc4G9zcfNbrixnfM/N6u1J8jPXK9GSo5/JXPA+X1tzC07DpyBDTFmd9gfJ8y/nLP2NcuaZg/mv0tyujk9/W/tHVV7kdza1jbvt7tj8FmxYgW33HILaWlpeHl54e/vj5dX7iJKaFiRiNvw9DBbdZrVgNsvrX1xIhmejTIXH3x7zeVzC7JdRX7ua2MGn5k7zI1W85tavefSVNQWau0pVTabOZOsSfXL46oS02Dbpa6wHSdh10lzenrypYHSz3bPvXmsiCO1vrQMRMw5s/U4v67a0mLp/x7PPvssGRkZfPHFF4wcORJPTyfZmEPEDdSpDNMGmWOAXlkBSelma1Fh95y60m1N4eUV5oDrNUfNBRjzkrVVhbOsvFqW+ZU3/52u/LdKvWh2lV7MLPx+ZyIlrUp5cwPfrHE+Rdkux0qW7h3xxx9/cO+99zJ69GiFHpESYLOZa74secC8/+eNxVsAr2K5yy1Ks3bkf95uBR+nVrGcuVigQo84qzaXurv+jHNsPcDi4FOpUiVq165t5SVFJA91KpuDnMfcUPxrZS1g+OsBsxn6apn2y11dLRV8RKQI2l5azcYZBjhbGnxuvfVWfv/9dysvKSIlrE1t85aeaS6qd7UjieZ6Nj5eEOxX+vUTEdfnTAOcLQ0+77zzDmfPnuXvf/87qampVl5aRErQfZc2Gv3fDnMm0ZWyxvc0q37tBRVFRPJz9QBnR7J0cPO9995L5cqVmTx5MtOnT6dZs2Z5rqBos9mIioqysmgRKYbbm5tbWOw/DZuO51y0T+N7RKS4fMub+7kdOuv4Ac6WBp/ly5dnP05OTmbLli15nmfTNr0iTqVKeRjQzFxReub2q4KPxveIiAXa1r4UfOIcG3wsbbi22+0FuuW1qKGIOFbWIOcF+yAu+fLrZXGrChGxnrMMcFaPvYgAcEMdc4HCCxnQfwb8tBdS0uGvS5uqavFCESkOZxngXOrBJz09naSkpNIuVkSuw2aDj28zN0M9cwHGLYT755nHalfS3k8iUjxZA5yPOXiAc7GDT6NGjZg0aVKO1xYtWkRkZGSe57/55ptUq1atuMWKSAloXA1+vAee7AJeHpc3SFVrj4gUV9YAZ3Bsd1exg8/hw4c5e/ZsjtfWrVvHxIkTi3tpEXGAcp4wvivMu+dy4OkUcO33iIgURFZ31zYHruCsrexEJE9ta8OP95qbYbav4+jaiIg7aFMbftzr2BYfBR8RyVd5LwjV/k8iYhFnGOCsWV0iIiJSKrI2Kz12Ds44aICzWnxERESkVPiWh+Y1zL3/Es5DtQqlXwcFHxERESk1i4aby2c4iiXB55tvvmHdunXZz/fv3w+Yu7VfLeuYiIiIlD2O3rXKZhhX78VcOB4ehR8mZLPZtG3FVZKSkvDz8yMxMTHPjV1FREQkb4X5Di12i8+hQ4eKewkRERGRUlHs4BMc7MAtVkVEREQKQdPZRUREpMxQ8BEREZEyQ8FHREREygwFHwstWLCA5s2b07RpU7744gtHV0dERESuogUMLZKRkUFkZCTLli3Dz8+Pjh07MmTIEGrUqOHoqomIiMglavGxyIYNG2jdujWBgYFUrlyZiIgIFi9e7OhqiYiIyBUUfC5ZuXIlAwcOJCAgAJvNxrx583KdM3nyZBo0aICPjw9dunRhw4YN2cdiY2MJDLy8jXVgYCAxMTGlUXUREREpIAWfS1JSUggJCWHy5Ml5Hp81axaRkZG8+OKLbNmyhZCQEPr37098fHwp11RERESKSsHnkoiICF577TWGDBmS5/H333+fhx9+mFGjRtGqVSs+/fRTKlasyNSpUwEICAjI0cITExNDQEBAvuWlpaWRlJSU4yYiIiIlS4ObCyA9PZ3Nmzfz3HPPZb/m4eFBv379WLt2LQChoaFs376dmJgY/Pz8WLhwIRMmTMj3mm+++SYvv/xyrtcVgERERAon67uzINuPKvgUQEJCApmZmfj7++d43d/fn927dwPg5eXFe++9R1hYGHa7naeffvqaM7qee+45IiMjs5/HxMTQqlUr6tevXzI/hIiIiJs7d+4cfn5+1zxHwcdCgwYNYtCgQQU6t3z58pQvXz77eeXKlTl69ChVqlTBZrNZUp+kpCTq16/P0aNHteO7hfS5Wk+facnQ52o9fabWs+IzNQyDc+fOXXOISRYFnwKoWbMmnp6exMXF5Xg9Li6OOnXqWFKGh4cH9erVs+RaV/P19dX/oCVAn6v19JmWDH2u1tNnar3ifqbXa+nJosHNBeDt7U3Hjh2JiorKfs1utxMVFUW3bt0cWDMREREpDLX4XJKcnMz+/fuznx86dIjo6GiqV69OUFAQkZGRjBw5kk6dOhEaGsoHH3xASkoKo0aNcmCtRUREpDAUfC7ZtGkTYWFh2c+zBh6PHDmS6dOnc88993Dy5EleeOEFTpw4Qfv27fn1119zDXh2JuXLl+fFF1/MMZZIik+fq/X0mZYMfa7W02dqvdL+TG1GQeZ+iYiIiLgBjfERERGRMkPBR0RERMoMBR8REREpMxR8REREpMxQ8HFjkydPpkGDBvj4+NClSxc2bNjg6Cq5jDfffJPOnTtTpUoVateuzeDBg9mzZ0+Ocy5cuMDYsWOpUaMGlStXZujQobkWuZT8vfXWW9hsNp588sns1/SZFk1MTAz3338/NWrUoEKFCrRt25ZNmzZlHzcMgxdeeIG6detSoUIF+vXrx759+xxYY+eWmZnJhAkTaNiwIRUqVKBx48a8+uqrOfaB0md6fStXrmTgwIEEBARgs9mYN29ejuMF+QxPnz7N8OHD8fX1pWrVqjz44IMkJycXq14KPm5q1qxZREZG8uKLL7JlyxZCQkLo378/8fHxjq6aS1ixYgVjx45l3bp1LFmyhIsXL3LzzTeTkpKSfc748eP56aef+P7771mxYgWxsbHccccdDqy169i4cSOfffYZ7dq1y/G6PtPCO3PmDN27d6dcuXIsXLiQnTt38t5771GtWrXsc/7zn/8wadIkPv30U9avX0+lSpXo378/Fy5ccGDNndfbb7/NJ598wkcffcSuXbt4++23+c9//sOHH36YfY4+0+tLSUkhJCSEyZMn53m8IJ/h8OHD2bFjB0uWLGHBggWsXLmSMWPGFK9ihril0NBQY+zYsdnPMzMzjYCAAOPNN990YK1cV3x8vAEYK1asMAzDMM6ePWuUK1fO+P7777PP2bVrlwEYa9eudVQ1XcK5c+eMpk2bGkuWLDF69+5tPPHEE4Zh6DMtqmeeecbo0aNHvsftdrtRp04d45133sl+7ezZs0b58uWN//3vf6VRRZdz2223GaNHj87x2h133GEMHz7cMAx9pkUBGHPnzs1+XpDPcOfOnQZgbNy4MfuchQsXGjabzYiJiSlyXdTi44bS09PZvHkz/fr1y37Nw8ODfv36sXbtWgfWzHUlJiYCUL16dQA2b97MxYsXc3zGLVq0ICgoSJ/xdYwdO5bbbrstx2cH+kyL6scff6RTp07cdddd1K5dmw4dOvD5559nHz906BAnTpzI8bn6+fnRpUsXfa75uPHGG4mKimLv3r0A/PHHH6xatYqIiAhAn6kVCvIZrl27lqpVq9KpU6fsc/r164eHhwfr168vctlaudkNJSQkkJmZmWtVaX9/f3bv3u2gWrkuu93Ok08+Sffu3WnTpg0AJ06cwNvbm6pVq+Y419/fnxMnTjiglq5h5syZbNmyhY0bN+Y6ps+0aA4ePMgnn3xCZGQkzz//PBs3buTvf/873t7ejBw5Mvuzy+v3gT7XvD377LMkJSXRokULPD09yczM5PXXX2f48OEA+kwtUJDP8MSJE9SuXTvHcS8vL6pXr16sz1nBR+Q6xo4dy/bt21m1apWjq+LSjh49yhNPPMGSJUvw8fFxdHXcht1up1OnTrzxxhsAdOjQge3bt/Ppp58ycuRIB9fONX333XfMmDGDb7/9ltatWxMdHc2TTz5JQECAPlM3oK4uN1SzZk08PT1zzYaJi4ujTp06DqqVaxo3bhwLFixg2bJl1KtXL/v1OnXqkJ6eztmzZ3Ocr884f5s3byY+Pp4bbrgBLy8vvLy8WLFiBZMmTcLLywt/f399pkVQt25dWrVqleO1li1bcuTIEYDsz06/Dwrun//8J88++yz33nsvbdu25YEHHmD8+PG8+eabgD5TKxTkM6xTp06uCTkZGRmcPn26WJ+zgo8b8vb2pmPHjkRFRWW/ZrfbiYqKolu3bg6smeswDINx48Yxd+5cli5dSsOGDXMc79ixI+XKlcvxGe/Zs4cjR47oM85H37592bZtG9HR0dm3Tp06MXz48OzH+kwLr3v37rmWWti7dy/BwcEANGzYkDp16uT4XJOSkli/fr0+13ykpqbi4ZHz69HT0xO73Q7oM7VCQT7Dbt26cfbsWTZv3px9ztKlS7Hb7XTp0qXohRd5WLQ4tZkzZxrly5c3pk+fbuzcudMYM2aMUbVqVePEiROOrppLeOyxxww/Pz9j+fLlxvHjx7Nvqamp2ec8+uijRlBQkLF06VJj06ZNRrdu3Yxu3bo5sNau58pZXYahz7QoNmzYYHh5eRmvv/66sW/fPmPGjBlGxYoVjW+++Sb7nLfeesuoWrWqMX/+fOPPP/80br/9dqNhw4bG+fPnHVhz5zVy5EgjMDDQWLBggXHo0CFjzpw5Rs2aNY2nn346+xx9ptd37tw5Y+vWrcbWrVsNwHj//feNrVu3Gn/99ZdhGAX7DG+55RajQ4cOxvr1641Vq1YZTZs2Ne67775i1UvBx419+OGHRlBQkOHt7W2EhoYa69atc3SVXAaQ523atGnZ55w/f974f//v/xnVqlUzKlasaAwZMsQ4fvy44yrtgq4OPvpMi+ann34y2rRpY5QvX95o0aKF8X//9385jtvtdmPChAmGv7+/Ub58eaNv377Gnj17HFRb55eUlGQ88cQTRlBQkOHj42M0atTI+Ne//mWkpaVln6PP9PqWLVuW5+/RkSNHGoZRsM/w1KlTxn333WdUrlzZ8PX1NUaNGmWcO3euWPWyGcYVS1GKiIiIuDGN8REREZEyQ8FHREREygwFHxERESkzFHxERESkzFDwERERkTJDwUdERETKDAUfERERKTMUfERERKTMUPARERGRMkPBR0RERMoMBR8REREpMxR8REREpMxQ8BEREZEyQ8FHREREygwFHxERESkzFHxERESkzFDwERERkTJDwUdERETKDAUfERERKTMUfERERKTMUPARERGRMkPBR0RERMoMBR8REREpMxR8REREpMxQ8BEREZEyQ8FHREREygwFHxERESkzFHxERESkzFDwERERkTJDwUdERETKDAUfERERKTMUfERERKTMUPARERGRMkPBR0RERMoMBR8REREpMxR8REREpMxQ8BEREZEyQ8FHREREygwFHxERESkzFHxERESkzFDwERERkTJDwUdERETKDAUfERERKTMUfERERKTMUPARERGRMkPBR0RERMoMBR8REREpM7wcXQEx2e12YmNjqVKlCjabzdHVERERcRmGYXDu3DkCAgLw8Lh2m46Cj5OIjY2lfv36jq6GiIiIyzp69Cj16tW75jkKPk6iSpUqgPmP5uvr6+DaiIiIuI6kpCTq16+f/V16LQo+TiKre8vX11fBR0REpAgKMlREg5tFRESkzFDwERERkTJDwUdERETKDAUfERERKTMUfERERKTMUPARERGRMsPS6ezLli0jKiqK1atXc+zYMRISEqhYsSK1atWibdu29O7dmwEDBlCnTh0rixUREREpEJthGEZxLpCSksKkSZP4/PPP+euvv8i6nI+PD9WrV+f8+fMkJiZit9sBKFeuHAMHDmT8+PF07969+D+Bm0hKSsLPz4/ExESt4yMiIlIIhfkOLVZX16effkqTJk3417/+ha+vL6+++ipRUVEkJiaSmprKsWPHOHXqFBcvXmT37t18+eWX3H333SxevJhevXpxxx13cOjQoeJUQURERKTAitXiU65cOe677z6efvpp2rRpU+D3nT9/nhkzZvDmm28ycuRIXnjhhaJWwW2oxUdERKRoCvMdWqzgs3fvXpo1a1bUt5OZmcmRI0do2LBhka/hLhR8REREiqbUurqKE3oAPD09FXpK0Oqj8PkWOHTG0TURERFxDtqk1I19sgl+PwJ+5aFhNUfXRkRExPFKJfjs27eP6Ojo7Nsff/zBsWPHSqPoMi3YD34H/kp0dE1EREScQ6GDz+bNm3nhhRc4cOAAnTp14p133qFu3boApKWl8eeff+YIOdu2bSMlJQUge6p7QbaNl+ILrmreK/iIiIiYChV8Dh48SFhYGL179+b1119n2rRp9O3blw4dOhAdHc2+ffvIzMwEyLGej2EYtG7dmgcffJDWrVsXagaYFF0DP/P+r7MOrYaIiIjTKFTwWbBgASkpKXzzzTf4+fnRt29fqlevzp49e/Dw8KBJkya0adOGNm3a0LZtW9q0aUPjxo0pV64c3bp148knnyyhH0PyEnwp+BxWi4+IiAhQyOATEBCAYRisWbOGiIgI1qxZA5hdV0888QQvv/wylSpVKpGKSuEFXQo+SWlw9gJU9XFsfURERBytUNPZhw4dyqBBgxg4cCCNGzdm3Lhx/Oc//6FWrVr897//pWnTpnzxxRcUcxcMsUiFcuB/KYcePuvQqoiIiDiFQgUfm83GvHnzWLt2LRMnTmTr1q384x//YN++fTz99NOcOXOGRx55hJCQEBYvXlxSdZZCaFDVvNcAZxERkSIuYNi5c2cGDBiAn5/Zl1K5cmXefPNNdu/ezZ133sn27duJiIggIiKC7du3W1phKZys7i61+IiIiBRz5earBQcHM2vWLFatWkWnTp1YtGgRHTp00PR1B8qe2aUWHxEREWuDT5Ybb7yR9evX8/XXX1O3bl0Mw2DmzJm88847ZGRklESRko/stXzOOrIWIiIizqFEgk+W4cOHs3fvXl5++WUAnn32Wdq1a8eSJUtKsli5glp8RERELivR4APmAoYTJkxg7969jBw5kr179xIREVHSxcolQVXN+5OpkJLu0KqIiIg4XLGDz8cff0xMTMx1z6tTpw5Tp05l48aN9OrVq7jFSgH5lYdql9bvUauPiIiUdcUOPuPGjSMoKIjOnTvz+uuvs23btmue36FDB5YuXVrcYqUQgtXdJSIiAlgQfDZu3Mjzzz9Peno6EyZMoH379jRu3JinnnqKFStWYLfbrainFIMGOIuIiJiKHXw6duzIq6++yh9//MHBgwd59913CQoKYtKkSYSHh+Pv78+oUaOYN28eqampVtRZCkktPiIiIiZLBzc3aNCA8ePHs2zZMuLi4pg2bRo9e/Zk9uzZ3HHHHdSsWZOBAwcydepU4uPjrSxariFr9WYtYigiImWdzSiFjbXS0tJYsmQJ8+fPZ8GCBcTFxeHh4UHXrl1ZtWpVSRfvEpKSkvDz8yMxMRFfX19Lr70xFu78HupVgdWjLb20iIiIwxXmO7RQu7MXVfny5RkwYAADBgzAMAzWrl3L/Pnz+fHHH0uj+DIvay2fmHOQlgHlS+VfXURExPmU+Do+V7PZbNx44428/fbb7Nq1q7SLdzqTJ0+mVatWdO7cucTKqFkRKpYDAzh2rsSKERERcXrF6uoaPbpo/SY2m40pU6YUtVi3VJJdXQARM2BnAkwdBH0bWn55ERERhym1rq7p06cX6X0KPqUvuKoZfI5oZpeIiJRhxQo+hw4dsqoeUsKyprRrZpeIiJRlxQo+wcHBVtVDSljWlHat5SMiImVZqQ9uFscIylrE8KxDqyEiIuJQJTKxefXq1UyfPp3o6GiSkpLw9fWlQ4cOjBgxgh49epREkXIdWVPajyZBph08FXlFRKQMsjz4jB8/nkmTJpE1Wcxms2EYBps3b2bKlCk88cQTvP/++1YXK9dRpzJ4e0J6JsQmQ33rJ46JiIg4PUv/7v/yyy+ZOHEiTZs2ZcaMGcTGxpKRkcHx48f59ttvadasGRMnTuSrr76yslgpAE+Py2FH3V0iIlJWWbplRdeuXYmNjWXbtm34+fnlOp6YmEjbtm0JCAhg3bp1VhXrFkp6HR+AUfNh6WF4IxyGty2RIkREREpdYb5DLW3x2bFjB0OHDs0z9AD4+fkxdOhQduzYYWWxUkDarFRERMo6h2xZIY4RXNW8P3TWkbUQERFxHEuDT+vWrfnhhx9ITk7O8/i5c+f44YcfaN26tZXFSgE1q27e7znl2HqIiIg4iqXB55FHHuHYsWN069aNH374gYSEBAASEhKYPXs2N954I8eOHeOxxx6zslgpoOY1zPsjiZB60bF1ERERcQRLp7OPGjWKrVu38tFHH3H33XcD4OHhgd1uB8AwDB5//HFGjhxpZbFSQDUqQq2KcDIV9p6C9nUcXSMREZHSZfk6PpMmTeKuu+7KcwHDkSNH0rNnT6uLlEJoVsMMPnsUfEREpAwqkZWbe/bsqYDjpFrUgNVHNc5HRETKJm1cUMY0uzTOZ0+CY+shIiLiCCXS4pOZmcmxY8eIjY3l4sW8R9H26tWrJIqW62he07xXi4+IiJRFlgYfu93OG2+8wcSJEzl9+vQ1z83MzLSyaCmgrCntJ1Ph9HmoXsGx9RERESlNlgaf5557jnfeeYfatWszatQo6tati5dXiTQqSRFV8jb37DqaZLb6dKvn6BqJiIiUHktTyZdffknz5s3ZuHEjlStXtvLSYqHmNRR8RESkbLJ0cHNycjK33XabQo+Tyx7nowHOIiJSxlgafNq1a0dsbKyVl5QSkLWCswY4i4hIWWNp8PnXv/7FvHnz2LJli5WXFYu1uBR89p4Cw3BsXUREREqTpWN8brvtNqZPn05ERASDBg0iJCQEX1/fPM8dMWKElUVLITSsBl4ecC4dYs9BYN7/RCIiIm7H0uCTlpbGTz/9REJCAlOmTAHAZrPlOMcwDGw2m4KPA3l7QqNqZovPnlMKPiIiUnZYGnwiIyOZMWMG7dq1484779R0difWosbl4BPe0NG1ERERKR2WppLvv/+ejh07snbtWgUeJ9dMA5xFRKQMsnRw84ULFwgLC1PocQHNtWeXiIiUQZYGn44dO7J//34rLyklpMWltXz2n4EMu2PrIiIiUlosDT5vvPEGv/76KwsWLLDyslIC6vlCxXKQngmHzzq6NiIiIqXD0j6pJUuW0KdPH26//XbCw8Pznc5us9mYMGGClUVLIXnYzA1Lo+PMcT5Nqju6RiIiIiXPZhjWLWHn4VGwBiSbzabd2a+SlJSEn58fiYmJ+a59ZLV/LoHvdsIToRDZrVSKFBERsVxhvkMtbfFZtmyZlZeTEpY1wHm3ZnaJiEgZYWnw6d27t5WXkxLWQpuViohIGVPswc0ff/wxMTExVtRFSlnWWj5/JcKFDMfWRUREpDQUO/iMGzeOoKAgOnfuzOuvv862bdusqJeUgloVoZoPGMC+046ujYiISMkrdvDZuHEjzz//POnp6UyYMIH27dvTuHFjnnrqKVasWIHdrkVinJXNdnmczz6N8xERkTKg2MGnY8eOvPrqq/zxxx8cPHiQd999l6CgICZNmkR4eDj+/v6MGjWKefPmkZqaakWdxULaukJERMoSSxcwbNCgAePHj2fZsmXExcUxbdo0evbsyezZs7njjjuoWbMmAwcOZOrUqcTHx1tZtBSRgo+IiJQllq7jk5+0tDSWLFnC/PnzWbBgAXFxcXh4eNC1a1dWrVpV0sW7BEes4wOwIQbumg2BVWDN6FIrVkRExDIOW8cnP+XLl2fAgAEMGDAAwzBYu3Yt8+fP58cffyyN4uUaslp8Ys7BuTSoUt6x9RERESlJlnZ1FYTNZuPGG2/k7bffZteuXaVdvFylqg/4VzIfa2aXiIi4u2K1+IweXbS+EZvNxpQpU4pTtFioeQ2ISzHH+dxQ19G1ERERKTnFCj7Tp08v0vsUfJxL0xqw8gjs1QBnERFxc8UKPocOHbKqHuJAzTWzS0REyohiBZ/g4GCr6iEOlBV81OIjIiLurtQHN4vzaVrdvD+ZCqfPO7YuIiIiJanEprNnZmaSkJBAWlpanseDgoJKqmgppEreUN8XjiaZrT5d6zm6RiIiIiXD8uCzefNmnn/+eVauXEl6enqe59hsNjIytB24M2lewww+exR8RETEjVna1RUdHU3Pnj1Zu3YtN998M4Zh0K5dO26++WZq1qyJYRj07t2bBx54wMpixQLNNM5HRETKAEuDz6uvvgrA+vXrmT9/PgBDhgxh4cKFHD58mEcffZTt27fz4osvWlmsWEDBR0REygJLg8+qVasYNGgQLVu2zH4tayuwChUq8NFHHxEQEMDzzz9vZbFigSuntJf87m0iIiKOYWnwSUxMpFGjRtnPy5UrR3Jy8uXCPDzo06cPUVFRVhYrFmhUDTxtkJgG8SmOro2IiEjJsDT41K5dmzNnzmQ/r1OnDvv27ctxzoULF0hNTbWyWLGAjxc0qGo+1kKGIiLiriwNPq1atWLPnj3Zz7t3787ixYtZu3YtALt27eK7776jRYsWVhYrFtEKziIi4u4sDT633XYbK1eu5Pjx4wA888wzGIZBjx49qFWrFm3btuXs2bMa4+OkNMBZRETcnaXB59FHHyUmJoYaNcxv0JCQEKKiorjllluoWbMm/fr146effmLIkCFWFisWUfARERF3Z+kChuXKlcPf3z/HazfeeCM///yzlcVICcnes+s02A3wsDm2PiIiIlbTXl2SrUFV8PaE1ItwLMnRtREREbGepcFn9erVREZGcuLEiTyPHz9+nMjISNatW2dlsWIRLw9oVNV8vP+0Q6siIiJSIiwNPu+//z4//fQTderUyfN43bp1WbBgAf/973+tLNYpLViwgObNm9O0aVO++OILR1enwBpf2qn94JlrnyciIuKKLA0+GzdupEePHtc8p1evXm7f4pORkUFkZCRLly5l69atvPPOO5w65RojhhtVM+8PKPiIiIgbsjT4xMfHExgYeM1z6tSpQ3x8vJXFOp0NGzbQunVrAgMDqVy5MhERESxevNjR1SqQxgo+IiLixiwNPlWrVuXIkSPXPOevv/6icuXKxS7rrbfewmaz8eSTTxb7WldauXIlAwcOJCAgAJvNxrx58/I8b/LkyTRo0AAfHx+6dOnChg0bso/FxsbmCICBgYHExMRYWs+SkhV81NUlIiLuyNLg07VrV+bOncvRo0fzPH7kyBHmzZvHjTfeWKxyNm7cyGeffUa7du2ued7q1au5ePFirtd37txJXFxcnu9JSUkhJCSEyZMn53vdWbNmERkZyYsvvsiWLVsICQmhf//+btGSldXVdTLV3LdLRETEnVgafCIjI0lNTaV79+589dVX2Ss4Hz9+nC+//JLu3btz/vx5nnrqqSKXkZyczPDhw/n888+pVq1avufZ7XbGjh3LsGHDyMzMzH59z549hIeH8+WXX+b5voiICF577bVrLrL4/vvv8/DDDzNq1ChatWrFp59+SsWKFZk6dSoAAQEBOVp4YmJiCAgIKOyP6hCVvaHOpQY5tfqIiIi7sTT49OrVi/fff5/Y2FhGjRpFvXr18PLyol69eowePZoTJ04wceJEevXqVeQyxo4dy2233Ua/fv2ueZ6Hhwe//PILW7duZcSIEdjtdg4cOEB4eDiDBw/m6aefLlL56enpbN68OUf5Hh4e9OvXL3tPstDQULZv305MTAzJycksXLiQ/v3753m9yZMn06pVKzp37lyk+pSErCntBzSlXURE3IylKzcDPPHEE4SFhfHpp5+yceNGEhMTqVq1KqGhoTz66KO0adOmyNeeOXMmW7ZsYePGjQU6PyAggKVLl9KzZ0+GDRvG2rVr6devH5988kmR65CQkEBmZmauFar9/f3ZvXs3AF5eXrz33nuEhYVht9t5+umns7fxuNrYsWMZO3YsSUlJ+Pn5FbleVmpcHdYc0wBnERFxP5YHH4B27drx8ccf53s8MzMTT0/PQl3z6NGjPPHEEyxZsgQfH58Cvy8oKIivv/6a3r1706hRI6ZMmYLNVvJ7MQwaNIhBgwaVeDklQTO7RETEXVna1XWtAcFZMjMzuffeewt97c2bNxMfH88NN9yAl5cXXl5erFixgkmTJuHl5ZVjHM+V4uLiGDNmDAMHDiQ1NZXx48cXuuwr1axZE09Pz1yDo+Pi4vJduNHVKPiIiIi7sjT4/P3vf2f27Nn5Hrfb7dx7773MmTOn0Nfu27cv27ZtIzo6OvvWqVMnhg8fTnR0dJ4tSAkJCfTt25eWLVsyZ84coqKimDVrFv/4xz8KXX4Wb29vOnbsSFRUVI6fKyoqim7duhX5us4kK/j8dRYy7A6tioiIiKUs7erq0aMHDzzwADVq1CAsLCzHMbvdzn333ccPP/zAuHHjCn3tKlWq5BofVKlSJWrUqJHnuCG73U5ERATBwcHMmjULLy8vWrVqxZIlSwgPDycwMDDP1p/k5GT279+f/fzQoUNER0dTvXp1goKCAHP22siRI+nUqROhoaF88MEHpKSkMGrUqEL/XM6obhXw8YILGXA0ERrmP3lORETEpVgafH766Sd69uzJkCFDWL58Oe3btwfMEDJ8+HC+//57/t//+39MmjTJymLz5OHhwRtvvEHPnj3x9vbOfj0kJITffvuNWrVq5fm+TZs25QhtkZGRAIwcOZLp06cDcM8993Dy5EleeOEFTpw4Qfv27fn1119zDXh2VR42cz2fnSfN7i4FHxERcRc2wzAMKy944sQJunXrxoULF1i9ejUNGzbkvvvu47vvvuPRRx+95qDnsixrVldiYiK+vr6Org7jFsJPe+H5HvBIR0fXRkREJH+F+Q61dIwPmHtxLVq0iMzMTG6++WbuvvtuvvvuOx5++GGFHheiAc4iIuKOLA8+AM2aNeOXX34hPj6eOXPm8NBDD/HZZ5+VRFFSQrKDjxYxFBERN1KsMT6vvPLKNY+HhoYSHR1NQEBAjnNtNhsTJkwoTtFSwrL27Dp41qHVEBERsVSxxvh4eBStwchms+W77k5Z5WxjfFIvQstLPZPRY6BaBcfWR0REJD+F+Q4tVovPsmXLivN2cWIVy0FAZYhNNsf5dFLwERERN1Cs4NO7d2+r6iFOqHH1K4KPa2wuLyIick0lMrhZ3INmdomIiLtR8JF8ZQ9wVvARERE3Uazgc8stt7Bx48YivTclJYW33nqrQBubimNoSruIiLibYgWfkydP0rVrV8LCwpg2bRqJiYnXfc+6desYN24cwcHBvPrqq26zzYM7yt6sNBHSNQlPRETcQLG3rPjyyy95+eWXOXz4MB4eHjRv3pyOHTvi7+9P1apVuXDhAqdPn2bPnj1s2rSJc+fO4enpyb333strr72WvfFnWeds09kBDANafWJObY96AJpUd3SNREREcivMd6gle3UZhsEvv/zCtGnTWL58OadP5+4b8fDwoF27dgwZMoSHHnqIunXrFrdYt+KMwQdgwP9gWzz83wDo39jRtREREcmt1NbxyWKz2bjtttu47bbbANi1axfHjh3j1KlTVKhQgVq1atG6dWv8/PysKE5KUeNqZvDZe0rBR0REXJ8lwedqLVu2pGXLliVxaSllbWrDvD3wZ5yjayIiIlJ8ms4u19T+0tjzrSfMMT8iIiKuTMFHrqlNbfC0wclUiD3n6NqIiIgUj4KPXFOFctCipvk4Wt1dIiLi4hR85Lo61DHvo084th4iIiLFpeAj19VewUdERNyEgo9cV1bw2RYPGXbH1kVERKQ4LA0+np6eDB8+3MpLihNoXA18veF8Buw55ejaiIiIFJ2lwcfX15f69etbeUlxAh42aHdpWru6u0RExJVZGnxCQ0P5448/rLykOIms7q6tCj4iIuLCLA0+L730EkuXLuWrr76y8rLiBDTAWURE3IGlW1YsWbKEPn36MGrUKD788EM6d+6Mv78/Npstx3k2m40JEyZYWbSUsKwVnPefhnNpUKW8Y+sjIiJSFJbszp7Fw6NgDUg2m43MzEyrinULzro7+5W6T4Vj5+DbO6C7hnKJiIiTKPXd2bMsW7bMysuJk2lfxww+0ScUfERExDVZGnx69+5t5eXEybSvAwv2aZyPiIi4Li1gKAV25cwu7dQuIiKuyNIWnyyrV69m+vTpREdHk5SUhK+vLx06dGDEiBH06NGjJIqUUtC2Nnh5XN6pPdA5hyKJiIjky/LgM378eCZNmkTWmGmbzYZhGGzevJkpU6bwxBNP8P7771tdrJQCHy9zp/bt8eZO7Qo+IiLiaizt6vryyy+ZOHEiTZs2ZcaMGcTGxpKRkcHx48f59ttvadasGRMnTtQ6Py6svVZwFhERF2bpdPauXbsSGxvLtm3b8PPzy3U8MTGRtm3bEhAQwLp166wq1i24wnR2gNk74akl0KEOzLvH0bUREREp3HeopS0+O3bsYOjQoXmGHgA/Pz+GDh3Kjh07rCxWSlHWNPboE3DmvGPrIiIiUlilPqvr6lWcxbXUrQItaoABrDzi6NqIiIgUjqXBp3Xr1vzwww8kJyfnefzcuXP88MMPtG7d2spipZT1aWDeLz/syFqIiIgUnqXB55FHHuHYsWN069aNH374gYSEBAASEhKYPXs2N954I8eOHeOxxx6zslgpZVnBZ8VfYNd6PiIi4kIsnc4+atQotm7dykcffcTdd98NmPt32e12AAzD4PHHH2fkyJFWFiulrFNdqOwNp86bU9vb+Tu6RiIiIgVj+To+kyZN4q677spzAcORI0fSs2dPq4uUUlbO0xzkvOgALDus4CMiIq6jRFZu7tmzpwKOmwtrYAaf5X/BE10cXRsREZGCsXSMj6enJ8OHD7fykuKk+gSb99En4OwFx9ZFRESkoCwNPr6+vtSvX9/KS4qTqlsFmtcwBzev/MvRtRERESkYS4NPaGgof/zxh5WXFCeWPa1dwUdERFyEpcHnpZdeYunSpdqLq4zI6u5acVjT2kVExDVYOrh5yZIl9OnTh1GjRvHhhx/SuXNn/P39c63WbLPZmDBhgpVFiwN0CoBK5SDhPOyIh7aa3SUiIk7O0k1KPTwK1oBks9nIzMy0qli34CqblF5tzAJzdldkV83uEhERxyjMd6ilLT7Lli2z8nLiAjStXUREXImlwad3795WXk5cwJXT2k+fh+oVHFsfERGRa9E6PlIsdatAq1rm4OZlhx1dGxERkWvTOj5SbDc1NO+XHHRsPURERK5H6/hIsd3UyLxf8RdcyHBsXURERK5F6/hIsbWpDf6VIPUirD3m6NqIiIjkT+v4SLHZbGarzzfb4LeD5kwvERERZ6R1fJyEq67jk2X5YRg532z5Wf+gGYZERERKg9bxkVLXrZ65inNcCmzXKs4iIuKktI6PWKK8F/QKhoX7YfFBBR8REXFOlg5uLoj09HSSkpJKu1gpBVmzu37TtHYREXFSxQ4+jRo1YtKkSTleW7RoEZGRkXme/+abb1KtWrXiFitOKKwBeNhgZwIcU7YVEREnVOzgc/jwYc6ePZvjtXXr1jFx4sTiXlpcTPUK0Kmu+fi3Q46ti4iISF5KvatL3NtNjc17dXeJiIgzUvARS2VtX7HuGCSlObYuIiIiV1PwEUs1rAaNq8FFOyw+4OjaiIiI5KTgI5Yb3MK8/36XY+shIiJyNQUfsdydLcGG2d11JNHRtREREbnMkgUMv/nmG9atW5f9fP/+/QDceuutuc7NOibuK6AK9AiC34/A7J0Q2c3RNRIRETEVe6+ugu7PlaNQ7dWVi6vv1XW1+Xvg779CvSrw+yhzfR8REZGSUKp7dR06pAVbJLf+jcHXG46dgzVHzRYgERERRyt28AkODraiHuJmfLxgYDOYsR2+36ngIyIizkGDm6XE3NXavF+4X2v6iIiIc1DwkRLT3h+aVIe0TFiw19G1ERERUfCREmSzwV2tzMff7XRsXUREREDBR0rYHS3A0wZbT8C+046ujYiIlHUKPlKialeCPg3MxzO2ObQqIiIiCj5S8kaFmPffboPj5xxbFxERKdsUfErIggULaN68OU2bNuWLL75wdHUcqkcQdAk0Bzl/tNHRtRERkbJMwacEZGRkEBkZydKlS9m6dSvvvPMOp06dcnS1HMZmg6cubVsxc4f27xIREcexZK+uK6WnpzNv3jw2btzI2bNn89yawmazMWXKFKuLdhobNmygdevWBAYGAhAREcHixYu57777HFwzx+kSCL2CYOURmLQe3r3Z0TUSEZGyyNLg89dff3HTTTdx4MABrrUFWFGDzyeffMInn3zC4cOHAWjdujUvvPACERERRa1yLitXruSdd95h8+bNHD9+nLlz5zJ48OBc502ePJl33nmHEydOEBISwocffkhoaCgAsbGx2aEHIDAwkJiYGMvq6Kqe6mYGnx92w2OdoXE1R9dIRETKGku7usaPH8/+/fu5//77WbZsGfv27ePQoUO5bgcPHizS9evVq8dbb73F5s2b2bRpE+Hh4dx+++3s2LEjz/NXr17NxYsXc72+c+dO4uLi8nxPSkoKISEhTJ48Od96zJo1i8jISF588UW2bNlCSEgI/fv3Jz4+vkg/V1nRvg7c1AjsBnywztG1ERGRMsmwkJ+fn9GvXz8rL3ld1apVM7744otcr2dmZhohISHGnXfeaWRkZGS/vnv3bsPf3994++23r3ttwJg7d26u10NDQ42xY8fmKCsgIMB48803DcMwjNWrVxuDBw/OPv7EE08YM2bMuGZZiYmJBmAkJiZet16ubEe8YQR9YN52xju6NiIi4g4K8x1qaYuP3W6nQ4cOVl4yX5mZmcycOZOUlBS6deuW67iHhwe//PILW7duZcSIEdjtdg4cOEB4eDiDBw/m6aefLlK56enpbN68mX79+uUoq1+/fqxduxaA0NBQtm/fTkxMDMnJySxcuJD+/fvneb3JkyfTqlUrOnfuXKT6uJpWtWBAU/Px66sg0+7Y+oiISNliafDp0qULu3btsvKSuWzbto3KlStTvnx5Hn30UebOnUurVq3yPDcgIIClS5eyatUqhg0bRnh4OP369eOTTz4pcvkJCQlkZmbi7++f43V/f39OnDgBgJeXF++99x5hYWG0b9+ep556iho1auR5vbFjx7Jz5042biw787zHd4XynvD7EXhnjaNrIyIiZYmlweett95i6dKlzJ4928rL5tC8eXOio6NZv349jz32GCNHjmTnzvw3ggoKCuLrr79m1qxZeHl5MWXKFGw2W4nVL8ugQYPYu3cv+/fvZ8yYMSVenitpUh3evtRg9slmmLPbsfUREZGyw9JZXT///DNhYWHcc8899O7dmxtuuAFfX99c59lsNiZMmFCkMry9vWnSpAkAHTt2ZOPGjUycOJHPPvssz/Pj4uIYM2YMAwcOZOPGjYwfP54PP/ywSGUD1KxZE09Pz1yDo+Pi4qhTp06Rr1vWDGkB+07B5E3w7G/QsCp00McnIiIlzNLg89JLL2U/Xr58OcuXL8/zvOIEn6vZ7XbS0tLyPJaQkEDfvn1p2bIl33//PXv37qVPnz6UL1+ed999t0jleXt707FjR6KiorKnudvtdqKiohg3blxRf4wy6R83mhuXLj4ID/8EP90Ldas4ulYiIuLOLA0+y5Yts/JyuTz33HNEREQQFBTEuXPn+Pbbb1m+fDmLFi3Kda7dbiciIoLg4ODsbq5WrVqxZMkSwsPDCQwMZPz48bnel5yczP79+7OfHzp0iOjoaKpXr05QUBAAkZGRjBw5kk6dOhEaGsoHH3xASkoKo0aNKrkf3g152OCD/jD0e9iVAA8tgO/vhIrlHF0zERFxVzbDuMZKg07mwQcfJCoqiuPHj+Pn50e7du145plnuOmmm/I8f8mSJfTs2RMfH58cr2/dupVatWpRr169XO9Zvnw5YWFhuV4fOXIk06dPz37+0UcfZS9g2L59eyZNmkSXLl2K/LMlJSXh5+dHYmJint2D7uxYEgyaCafOQ//G8OltZigSEREpiMJ8h7pU8HFnZTn4AGyKhWFzzI1MH+0Iz/VwdI1ERMRVFOY7tEQ2KV29ejUPP/wwnTt3pnnz5nTu3JkxY8awatWqkihO3ECnAPjPpZlen26G/213bH1ERMQ9Wd7iM378eCZNmpS9V5fNZsvx+IknnuD999+3ski3UNZbfLJ8sA7+ux68PODL26FHkKNrJCIizs5hLT5ffvklEydOpGnTpsyYMYPY2FgyMjI4fvw43377Lc2aNWPixIl89dVXVhYrbuSJLnB7c8iww2O/wK6Tjq6RiIi4E0tbfLp27UpsbCzbtm3Dz88v1/HExETatm1LQEAA69Zpl8orqcXnsgsZ5nifzcehqg98MwTa1nZ0rURExFk5rMVnx44dDB06NM/QA+Dn58fQoUPz3U1dBMDHC6bdbi5oePYCDPsBtp5wdK1ERMQdlMjg5mspje0ixPX5lYevB0PnAEhKh+FzYEOMo2slIiKuztLg07p1a3744QeSk5PzPH7u3Dl++OEHWrdubWWx4qaqlIevBsON9SDlIoyYB7//5ehaiYiIK7M0+DzyyCMcO3aMbt268cMPP5CQkACYW0fMnj2bG2+8kWPHjvHYY49ZWay4sYrlzG6v3sFwPgP+9iPMzn9PWhERkWuyfDr73//+dz766KPsLi0PDw/sdjsAhmHw+OOPM3HiRCuLdAsa3HxtaRnwjyXw417zeWRX+HsoqOdUREQcvnLz77//zvTp04mOjiYpKQlfX186dOjAyJEj6dmzp9XFuQUFn+uzG/DOGvh4k/n8rpbwZl8o5+nYeomIiGM5PPhI4Sn4FNyMbfDvZWYQ6lEfPr7NHAwtIiJlk8O3rBApScPbwpSB5vifVUdhyCw4fNbRtRIREVdQrBaf0aNHY7PZeOONN/D392f06NEFK9RmY8qUKUUt1i2pxafwdpyEh36E2GRzocNPb4Nu9RxdKxERKW2l1tXl4eGBzWZj165dNGvWDA+PgjUg2Ww2MjMzi1qsW1LwKZr4FHj4J4iOM/f3ej0M7m3j6FqJiEhpKsx3qFdxCjp06BAAgYGBOZ6LlJbalWDWneaMr5/2wjNRsPc0/KsHeKojV0RErqLBzU5CLT7FYxjwwXrzBhDWAD68xVwEUURE3JvDBjcfOXKEpKSka55z7tw5jhw5YmWxIthsML4rTI6A8p6w7DAM+Q6OJDq6ZiIi4kwsDT4NGza87uKEkyZNomHDhlYWK5JtQDOYfRf4V4J9p2HQTFh3zNG1EhERZ2Fp8DEMg+v1nKlnTUpaO3/48V5oVxvOXIDhc821f0REREp9+OexY8eoUqVKaRcrZUydyvD9XTCoGWTY4fmlMGEZXNRkQhGRMq1Ys7oAXnnllRzPly9fnud5mZmZHD16lJkzZ9K1a9fiFityXT5eMOkWaF4D3lkLX/1pdn99citUq+Do2omIiCMUe1bXlWv32Gy263ZlBQQEMHfuXDp37lycYt2OZnWVrMUH4MlFkHIR6vnC/w2A1rUcXSsREbFCqe7VtWLFCsAcuxMeHs7f/vY3Ro4cmes8T09PqlevTosWLQq80GFZouBT8vYkwEMLzJlePl7wVl8Y0sLRtRIRkeJy2CalL7/8MmFhYfTq1cuqS5YZCj6l4+wF+PuvsOIv8/no9vB8D+3wLiLiyrQ7uwtS8Ck9mXZ4fx18tNF83iXQXOzQv7Jj6yUiIkVTaltWXEtmZiYJCQmkpaXleTwoKKikiha5Jk8P+OeN5rT3yMWwPgZu/RYm3gI99J+liIhbs7zFZ/PmzTz//POsXLmS9PT0vAu12cjIyLCyWJenFh/HOHgG/t8vsCsBbMATXeDvodrnS0TElThsy4ro6Gh69uzJ2rVrufnmmzEMg3bt2nHzzTdTs2ZNDMOgd+/ePPDAA1YWK1JkjarBvHvg3tZgYO719cA8iEtxdM1ERKQkWBp8Xn31VQDWr1/P/PnzARgyZAgLFy7k8OHDPProo2zfvp0XX3zRymJFisXHC97uB/+9GSp4weqjcMsM+O2go2smIiJWszT4rFq1ikGDBtGyZcvs17J60ipUqMBHH31EQEAAzz//vJXFiljijpbw033QqiacPg8P/gT/WgrnLzq6ZiIiYhVLg09iYiKNGjXKfl6uXDmSk5MvF+bhQZ8+fYiKirKyWBHLNK1udn091MF8/s02GDAT5u2GlLyHrImIiAuxdFZX7dq1OXPmTPbzOnXqsG/fvhznXLhwgdTUVCuLFbFUeS+Y0At6B5uzvvafhicWmd1gNzWCwc2hV7DW/hERcUWWtvi0atWKPXv2ZD/v3r07ixcvZu3atQDs2rWL7777jhYttFyuOL9ewbD4fngiFIL94HwG/LgXRv8Et/4P/jjh6BqKiEhhWRp8brvtNlauXMnx48cBeOaZZzAMgx49elCrVi3atm3L2bNnNcZHXEb1ChDZDVaMhB/vMVd6ruYDe0/B4O/grVVwQSsziIi4DEvX8bl48SKnT5+mWrVqeHt7A7BmzRpef/11Dh48SHBwMI8//ji33XabVUW6Da3j4zpOn4eXVsD8S42bjavBuzfBDXUdWy8RkbJKW1a4IAUf17PogDnr62Squfjh8Lbw9I3g5+PomomIlC0OW8BQpCzp3xh+ewCGtjQXP/xmG4R/BXN2g/6cEBFxTsVq8Rk9enTRCrXZmDJlSlGLdUtq8XFta4+ZrT8HLk1q7FYPXu4NzWs6tl4iImVBqXV1eXjk3WBks9nI67JZr9tsNjIzM4tarFtS8HF96Znw+RaYuB7SMsHDZnZ/RXY1B0mLiEjJKLWurkOHDuW4HThwgAEDBlCjRg1effVVli9fzq5du1i+fDmvvPIKNWrUYODAgbnW9hFxB96eMLaz2f0V0QTsBnz9J/T+EqZuhYvK+iIiDmfp4Oa33nqL//73v0RHR1O3bu4pLjExMXTo0IF//OMfPP3001YV6xbU4uN+1h6Dl1eYO7+DOfvrXz0gvCHYbI6tm4iIO3HY4OYpU6Zw99135xl6AAIDA7n77rv5/PPPrSxWxCl1qwc/3wdvhptdXQfOmIsfDp8Lu046unYiImWTpcHn2LFj+Phcey6vj48Px44ds7JYEafl6QHD2poLID7a0ewOW33UXPn52ShI0O4tIiKlytKurqZNm2IYBtu3b88zAKX+//buPKzqMu/j+PscdmUTEBAVxNQUTTMVcNBwIW2ZyqypzMrUapqoXHrGaZppamYqp5qaSnvqmSWraTNt1HTSIvctItPUUNQUd8GVRUCE83v+uBUlcIOjh8P5vK7rd+n5nfv87pv7Us73urdvSQlXXHEFdrtd63x+QlNdnmFHAbywHOac+Ocf7AtjkmBEN+X+EhGpK5dNdd1///1s3bqVlJQUZs2axcGDBwE4ePAgM2fOpE+fPuTm5vLAAw84s1oRtxEbAm9cD9Nvg87NobAc/rwUBn8Ai7e7unUiIo2fU0d8HA4HDzzwAFOmTMF2YvWm3W7H4XAAYFkWI0eO5J///GfV+2JoxMfzVDrgk2x4cYVJgwEmI/zv+0KHcNe2TUTEnbg8ZcXixYt59913Wbt2LQUFBYSEhNCtWzfuuece+vXr5+zqGgUFPp6r4Bi89jW8uxYqHOb8n2GdYVwyNG/q6taJiDR8Lg985MIp8JFth2HicpMDDKCpD9zfHe6/CoL9XNs2EZGGTLm6RNxQfDP4+8/hk9ugayQcPQ6vfQN9psAbWXC03NUtFBFxfxrxaSA04iOnc1gwbwu88jVsPmTuhQdAn1iID4U2oebPhOZmi7yIiCe7kO9Q7/pUNGrUKGw2G88//zxRUVHnnbRUSUpFzs5ug+vbmwzwn22CV7+G3AKYlVO9XNtQ+OhWiA50STNFRNxOvZOU2mw2NmzYQIcOHc6YtLRGpUpSWoNGfORsKhywONeM/mw7ArlHIPsAFB4zqTCm3qqF0CLiuS7ZiM+2bdsAk4ri9Nci4lzedhjY1lwn7SqEX0wzqTDungEf3wrNlAVeROSstMangdCIj9RF7hH4xXTIPwpdIuHDoRCiHWAi4mEu2YiPiLhWm1AT7NwxHdbnw9BPoEcLsxA6PMCs/enfBpr6urqlIiINQ70XN9eFFjeLOE/7MHj/FrjzU9hyyFynC/WHUVeafGChZ88hLCLS6NV7cXOdKtXi5ho01SX1tbcIFubCwdITVwmsyTOJUcEciHh3Vxh9JURpF5iINCKX7OTm7dvrnlUxLi6uzp9tjBT4yMVQ6YDPt5gDEDccMPe87XB9OxjVHbpHu7Z9IiLOoJQVbkiBj1xMlgULcuGtb+GbPafuXxkFd3aBfnHQIshlzRMRqRctbhaRamw2GBhvrnX58O4amLXJTIWtyTNl2ofB1XHQPw5+1hq8lNBGRBqhizbiU1lZyYEDBzh27Fit78fGxl6Mat2WRnzkUjtQAlN/gIyt8H2eSZNxUotA+EUC3N4ZWuufo4g0cC6d6lq1ahVPPvkkS5Ysoby89qyKNpuNiooKZ1br9hT4iCsdKYPlO2HJdpMd/nCZuW/D5Ad7so/JCyYi0hC5LDv7mjVr6Nu3LytXrmTQoEFYlkXXrl0ZNGgQERERWJZFamoq99xzjzOrFZF6CvWHG9rDC2mQORomXwd9WoMFLN0Bt04zI0MiIu7OqYHPn//8ZwAyMzOZNWsWALfccgtz584lNzeXhx56iPXr1/P00087s1oRcSI/b7ixA3wwFJbeBymtoeQ4PDAb/v6dWSgtIuKunBr4LFu2jJtuuolOnTpV3Ts5kxYQEMDkyZOJiYnhySefdGa1InKRxIbAuzfD8C5m9Oe5pfDEfCjXMVwi4qacGvgUFBTQtu2pLIo+Pj4UFxefqsxup1+/fsyfP9+Z1YrIReTjBc8NgKevBrsNPv4BBrwHzy6Fb/dUXxQtItLQOXU7e2RkJIcPH656HR0dzebNm6uVKSsro6SkxJnVishFZrOZAw/jQmHsPNhZCP/4zlzNm8C17eD2BLgi0pQVEWmonDrik5CQQE5OTtXrlJQUvvzyS1auXAnAhg0b+OSTT+jYsaMzqxWRS2RgPGTeD29eD0MuhyBf2F8C/14LN34M134A/1pt0mWIiDRETt3OPmnSJMaNG8fOnTtp0aIF33//PcnJyZSXlxMWFsbhw4dxOBx8+umn3HLLLc6qtlHQdnZxR+WVsGIn/GcjzNsCx06s/fGxwzVtYVgXsx3erlEgEbmIXHaOz/Hjxzl06BDNmjXD19cXgBUrVvDcc8+xdetW4uLiePTRR7nhhhucVWWjocBH3F1BGXy2CT75Adbmn7rfKhju6Ay/6KS0GCJycVzSwOfYsWP4+fnV5xGCAh9pXLL3w0frYeZGKDxxjqndBn1jzYnQ17QFfyXMEREnuaSBT1hYGHfddRejRo3iqquuqs+jPJoCH2mMyirg881mJ1jm7lP3Q/wguZUZDWoVBC2D4fJwaBPqsqaKiBu7pIFPkyZNKCsrw2az0a1bN0aPHs3w4cMJDQ2tz2M9jgIfaexyj8C0bPh0A+wtrr1MjxZmXdDP20OAzyVtnoi4sUsa+BQVFfHhhx/y9ttvk5WVhc1mw8/PjyFDhjB69GgGDhxYn8d7DAU+4ikqHWb0J+cg7C6CXYXmyt4PlSd+GwX5ws2Xw52doYu2yIvIObhscXN2djZvv/02H3zwAXl5edhsNmJjYxk1ahT33XcfrVu3dlZVjY4CH/F0ecUwfYOZFttRcOp+pwhzRtCQjhAW4Lr2iUjD5dLs7ACVlZXMnj2bt99+m3nz5lFRUYHdbueaa65h9OjR3Hzzzfj4aBz7dAp8RAyHZbbIT/3BZIo/fYt8WluzODo1DrydegqZiLgzlwc+p8vLy+O9995jypQpbNy4EZvNRnh4OPn5+ef+sAdR4CNSU0EZzMqBqdmw/rRfGc2bwNBOcFsn6BDuuvaJSMPQoAKfk9atW8fDDz/M8uXLsdlsVFYqy+HpFPiInF32fpieDTNy4FDpqftdI+G2BLipAzTTVJiIR2owgc/Jhc//+te/WLVqFZZl0bRpU26//Xb+9a9/Xaxq3ZICH5HzU14JC7aZHWKLtkOFw9z3sZuUGredmArz9XJtO0Xk0nF54LNw4ULefvttZsyYQWlpKZZlkZyczOjRo7njjjsIDAx0dpVuT4GPyIU7UGKmwqZvMCNCJ4UFmBGgWzspcaqIJ3BJ4LNr1y6mTJnCO++8Q25uLpZl0bx5c+655x5Gjx5Np06dnFFNo6XAR6R+svebnGEzN5rEqSe1C4OhHeGWjhCjlBkijdIlDXymTp3K22+/zYIFC6isrMRutzNo0KCq3Vve3jqX/nwo8BFxjgoHLN0B/9lQfVeYDXNa9NCOcF07CFKmHZFG45IGPna72VMaHx/PyJEjue+++2jVqlV9HumRFPiIOF/hMZi7xQRBX5+WMsPfGwa1NaNAV2trvIjbu6SBz/Dhwxk9ejQDBgyoz2M8ngIfkYtrVyHM2GiuHw+fuh8RADddbkaCdEq0iHty+eJmuXAKfEQuDcuCtXlmPdBnm6pvjW8XBrdcbk6JbqX/hiJuQ4GPG1LgI3LpHa+EJdvN2UBfnrYeCCCppZkKu74dhPi7ro0icm4KfNyQAh8R1yo6sR5oxkZYuQtO/mL0tkMTH/Onlw287GaL/H3dIKW1psZEGgIFPm5IgY9Iw7GnCD7LMdNhOQfPXK59GIy80owMNVH6QRGXUeDjhhT4iDRMe4qg5LhJnlrpgKPHzdqg6dnm7wDBvmZd0J1doHNz17ZXxBMp8HFDCnxE3EvhMRP8vPM9bC84db9rpAmAbuwAwTorSOSSUODjhhT4iLgnhwUrdsJH682BicdP5A7z94Yb2sPtCWahtNYCiVw8CnzckAIfEfd3sMSsC/r4B9hy6NT9uBCTPPXWjtBS/71FnO5CvkOdfl5pRUUFf/vb30hMTCQ4OLhayoo1a9bw8MMPs2nTJmdXKyLicuFN4IGr4Ku7YeYdMKwLBPqaqbCXV0LKFLjrPyY4Kjnu6taKeCanjviUlpYyaNAgVqxYQUREBD4+Puzdu5fKSnM4RkFBAdHR0Tz++OM8++yzzqq2UdCIj0jjVHLcbJOfng0rdp2639QHrm9vMsgntQS7psJE6sxlIz7PP/88y5cvZ+LEiezbt4/777+/2vshISGkpqbyxRdfOLNaEZEGq4mPCW4+uhWWjYTxyRAbYnaETcuGOz+FPlPgxRWw+dC5nyci9ePUwGfq1Kn079+fCRMmYLPZsNWymq9t27bs2LHDmdWKiLiF1sEwJgmWjIDpt5mpsGBf2F0Eb2RB2r/hho/gn99B3lFXt1akcfI+d5Hzt2PHDm655ZazlgkKCqKgoOCsZUREGjObDXq1NNczqfDVVnNi9KLtsD7fXM8tg5+1MglUr20HIdoaL+IUTg18goKCyM/PP2uZH3/8kebNdcKXiAiYbe8/72CuQ6UwZ5PJHfbdXli201y/Xwj925izgQbG65RokfpwauCTnJzM7NmzOXLkCKGhoTXe37lzJ59//vk5R4VERDxRWADc281c24+YE6Jn5Zi1P1/8aK4AbxP8/LyDCYb8nfpbXKTxc+oan1//+tccPnyYgQMHsnz5cioqKgAoKSlh/vz5DB48mIqKCsaPH+/MakVEGp24UHg0ETLuhnl3wcM9zRqh0gqYsxke+i9c9Xd4dC7M2wJlFTWfoVPaRGpy+gGGb775JmPGjKnawn46Ly8v/vd//7fGbi/RdnYROTfLgrV5MHsz/HcT7Ck+9V4TH+jRAorLzZTZoVKzcywxxkyRXd/ejCiJNEYuP7l5w4YNvPXWW2RmZnLo0CGCg4NJSkri4YcfpnPnzs6urlFQ4CMiF8JhwZp98N/N5pyg3UVnL+9lgz6xcPPlMKgtBGmxtDQiLg985MIp8BGRurIs+D4PNh6AUH8ID4CwJmYtw5dbzVqh9aftO/HzgmvamiAoNQ78tE5I3JzLAp/ly5fz6aefMmHCBKKjo2u8v3fvXl566SVuv/12kpOTnVVto6DAR0Qupq2HYfaJxdI/Hj51P9gPBrc1i6VTWoOPl+vaKFJXLgt8br31VtauXcvmzZvPWKZDhw50796dqVOnOqvaRkGBj4hcCpYF6/ebAOiznOoHJTbzN2cG3dAOklspCBL3cSHfoU4d4MzKymLgwIFnLXP11VeTkZHhzGpFROQ82WxwRaS5fpsCWXvMLrG5m+FAKXy03lyh/mYt0PXtzUiQr4IgaSScGvjk5+fTsmXLs5aJjo4+5yGHIiJy8XnZzchOcitzgvTXu8xi6S9+hIOl8Em2uYJ8YUA8DL4M+sVBU19Xt1yk7pwa+ISGhp4zD9f27dsJDAx0ZrUiIlJP3naz66tPLDzbH77ZA5+f2DG2v8RMjc3KMQuj+8aaxdFpbSGiiatbLnJhnLrGZ8iQIcyfP5/s7Gxat25d4/0dO3bQuXNnBgwYwKxZs5xVbaOgNT4i0hA5LFi9zxyS+MWPsP20VIs24KoWZkpsYFto18xMpYlcai5b3LxkyRL69+9Py5YtefbZZ7nmmmto0aIFe/fu5csvv+T3v/89e/fuZcGCBVx99dXOqrZRUOAjIg2dZUHOQRMAZWyFdT9ZtRAXAmnxZlossaXWBcml49JzfF577TUef/xxTj7WZrNV/d1ut/Pqq6+Snp7uzCobpDlz5vD444/jcDj4zW9+c87TqhX4iIi72VtkAqCvtsHKXVB+2oH9gb7Qp7UJgvq1gaimLmumeACXH2C4du1a3nrrLbKysigoKCA0NJTExEQeeughunTp4uzqGpyKigoSEhJYuHAhISEh9OjRgxUrVhAeHn7GzyjwERF3VlwOS3fA/K2wINcsjj5d5+YmAOoXB92jtVVenMvlgY+nW7FiBS+99BIzZswAYOzYsSQlJTFs2LAzfkaBj4g0Fg4L1uWZAGhhrjlV+nTBvtAh3GSWP3k1CzC5xpJaQkyQK1ot7uxCvkOdmp3dy8uL4cOHO/OR1UycOJFevXoRFBREZGQkQ4YMIScnx6l1LFmyhBtvvJGYmBhsNhszZ86stdwbb7xBmzZt8Pf3JykpiW+++abqvT179lTb1t+yZUt2797t1HaKiDRUdht0i4ZxyfDZnfDt/fC3QSZFRjN/KCyHb/fCsp1mmmzOZvj3Whj7BfR+G1KmwPgv4T8bqh+wKOIMTt3OHhwcXOtuLmdZvHgx6enp9OrVi4qKCp588kkGDRpEdnY2TZvWnEBevnw5iYmJ+Pj4VLufnZ1NeHg4UVFRNT5z9OhRunXrxqhRoxg6dGit7Zg6dSrjx4/nrbfeIikpiVdffZXBgweTk5NDZGSkc35YEZFGonlTGNrJXJUOkzdsdxGUVcKxCiirMK+/2W3e21Vork83mM93DDfb7K+OM9nmA3zOXp/I2Th1qmvw4MHY7Xbmzp3rrEee1f79+4mMjGTx4sU1dok5HA6uuuoq2rdvz8cff4yXl5lQzsnJITU1lfHjxzNhwoSzPt9mszFjxgyGDBlS7X5SUhK9evVi8uTJVXW1bt2aRx99lCeeeKLWqa7ExETuuuuuM9alqS4REbNW6Lu95jDFpTvMzrHTv6T8vKBXDPSNM+cJdYowI0zi2Vw21fXMM8+wYMEC3nvvPWc+9owKCsyBEmFhYTXes9vtfP7556xevZp7770Xh8PBjz/+yIABAxgyZMg5g54zKS8vZ9WqVaSlpVWrKy0tjZUrVwKQmJjI+vXr2b17N8XFxcydO5fBgwfX+rw33niDhIQEevXqVaf2iIg0JoG+ZmRnQgrMHgbfPQiTr4PbEyAmEI5Vmimyicvg+g+hxz/gkbkmzcbOQle3XtyBU6e6MjIy6NevHyNHjmTSpEn06tWLqKgobD850cpms/HUU0/Vqy6Hw8HYsWNJSUk5406xmJgYFixYQN++fbnrrrtYuXIlaWlpvPnmm3Wu98CBA1RWVtaYJouKimLjxo0AeHt78/LLL9O/f38cDgcTJkw4446u9PR00tPTq6JVERE5JSwAbuxgLssymeWX7oAl2+Hr3XCo1GSdn73JlG8dDD9rDT9rBb1baxu91OTUqS67/fwGkGw2G5WVlecueBa/+tWvmDt3LsuWLaNVq1ZnLbtkyRJSU1Np27YtOTk5eHufX7xX21TXyYXLK1asoHfv3lX3J0yYwOLFi8nMzKzTz6OpLhGRC1NeCd/vMyNAy3aYE6Yrf/KNdlkzs1MsuRUkt4QoZUxqlFyWnX3hwoXOfNwZPfLII8yZM4clS5acM+jJy8vjwQcf5MYbbyQrK4tx48YxadKkOtcdERGBl5cXeXnV92fm5eURHR1d5+eKiMiF8fWCXi3NNS7ZrA/K2gMrdsKKXfBDvhkh+vEwfLjefKZNiDlVOqml+bN1sNJseBqnBj6pqanOfFwNlmXx6KOPMmPGDBYtWkR8fPxZyx84cICBAwfSqVMnpk2bxqZNm+jXrx9+fn789a9/rVMbfH196dGjB/Pnz68aCXI4HMyfP59HHnmkTs8UEZH6C/SF/m3MBVBQZpKtfr3LTItl74fcAnN9km3KRAeaxdI9Y8yOscvDTdZ6abycGvhcbOnp6Xz44YfMmjWLoKAg9u3bB0BISAgBAQHVyjocDq677jri4uKYOnUq3t7eJCQkkJGRwYABA2jZsiXjxo2rUUdxcTFbtmyper1t2zbWrFlDWFgYsbGxAIwfP54RI0bQs2dPEhMTefXVVzl69CgjR468iD+9iIhciBB/k0X+mrbmdcExWLXHbJvP3GMOWdxXXH2NUJCvSbza48TVPRqa+rruZxDnuygnNy9fvpx33nmHNWvWUFhYSHBwMN27d+fee++lT58+dX7uTxdJnzRlyhTuu+++GvczMjLo27cv/v7+1e6vXr2a5s2b1zpNtmjRIvr371/j/ogRI3jnnXeqXk+ePJmXXnqJffv2ceWVV/L666+TlJR0YT/QabTGR0Tk0io9DmvyTCD07R5YtReOHq9exm6DED8zmnTyahEIHSPMVvqE5mYBtabLXMulKSvGjRvH66+/XmuSUpvNxpgxY3jllVecWWWjoMBHRMS1Khyw4YAJgFbtMcHQnuJzfy78RLqNnjFm2qxLpDLTX2ouC3zeffddRo4cSYcOHXj66afp378/UVFR5Ofns3DhQv74xz+yadMmpkyZwr333uusahsFBT4iIg1P/lE4UmYWTh8tN+k2dhSY9UIbDsDWwzV3kvl5wZXRJghKbAlXRUOQn2va7ylcFvgkJyezZ88e1q1bV+uZNAUFBVxxxRXExMTw9ddfO6vaRkGBj4iI+ymrMGk2vj0xSpS1Bw6XVS9jt0H7MLgi0owGXRFppsiaKPWG07hsO/sPP/zA/ffff8aD+EJCQrj11lv55z//6cxqRUREXMLf20xx9YwBepw6ZDFrz6lrRwHkHDTX9BP5x2xA22ZmndDJtUJdIiFSBy5edJd8V9eZFiiLiIi4O5sN2oWZa9iJpAJ5xbA23+wiW5dvrv0lp84YmrP51OejmpoRodNHhyK1eNqpLspUV3Z2NoGBNY/HLCoqokuXLrRo0UJTXT+hqS4REc+Rf9SsEdqwH344cW09XD0h60nNm5ggKCHC7CbrGAHxoeCjBdRVXDbV9ctf/pLRo0fTu3dvnnnmGVJTU4mIiODAgQMsWrSIP/7xj+zatYs//elPzqxWRETErUQ2NVdq3Kl7R8vNoun1+82o0Pp82HzIjA4tzDXXSb5e0DYUOoSb0aUO4dAyCA6WmrOJ8orhQCnEhZiziLpEmmk5uQjb2R977DEmT55cNaVlt9txOBzAqZOXX3vtNWdW2ShoxEdERH6q9LgZGVqXDxsPwMaDsOmg2WV2IXzsZh1R+zAzghTRBJo3PfHniSvU332n1Fx6jg/A0qVLaz3AcMSIEfTt29fZ1TUKCnxEROR8WBbsKjIB0OaDZlRo00HYdxQiAkwi1uhAaOYPWw7Bd3vN6M+5eNshLACC/SDQxxzW2NQXmvqYHWgnr2MVkHf01FVcbg55bOZvgqcQf9PGSsucjeSwTG60OztfvOk5lwc+cuEU+IiIyMVgWbCz0GSv31UIB0rM9Nn+Eth/1LwuOHbx23FZM3jq6lO51Jzpkq7xKSwsxN/fH19fJTMRERFpaGw2iA0x15mUV8LBEjMyVFx+6io6BiUVZsrt6HHzp48XRDeFyECzCy3I1ySEPXziKjxmzi7yspsptuJyeOd7s4PtvllmXdPv+5p1Sa5Q7xEfLy8vnnnmGZ566qmqe5mZmWRmZvLYY4/Vu4GeQiM+IiLSWBUeg0nfwJQ1cNwBXjZ4bwj0iXXS8y/gO9Re38osy+KnsdO8efNqzXwuIiIinifYD37XF766Bwa1hdbBJp2HK2hzm4iIiFwSbULhHzeaqTFXJXKt94iPiIiIyIUI8Xdd3Qp8RERExGMo8BERERGP4ZQ1Pu+//3613FtbtmwB4Prrr6+1vM1m47///a8zqhYRERE5b/Xezm63X/igkc1mo7Kysj7VNjrazi4iIlI3l/QAw23bttX3ESIiIiKXRL0Dn7i4uHMXEhEREWkAtLhZREREPIYCHxEREfEYCnxERETEYyjwEREREY+hwEdEREQ8hgIfERER8RjKzt5AnDxHsrCw0MUtERERcS8nvzvP50xmBT4NRFFREQCtW7d2cUtERETcU1FRESEhIWctU++UFeIcDoeDPXv2EBQUhM1mc8ozCwsLad26NTt37lQaDCdSvzqf+vTiUL86n/rU+ZzRp5ZlUVRURExMzDlTaWnEp4Gw2+20atXqojw7ODhY/0EvAvWr86lPLw71q/OpT52vvn16rpGek7S4WURERDyGAh8RERHxGAp8GjE/Pz+efvpp/Pz8XN2URkX96nzq04tD/ep86lPnu9R9qsXNIiIi4jE04iMiIiIeQ4GPiIiIeAwFPiIiIuIxFPiIiIiIx1Dg04i98cYbtGnTBn9/f5KSkvjmm29c3SS3MXHiRHr16kVQUBCRkZEMGTKEnJycamXKyspIT08nPDycwMBAbr31VvLy8lzUYvfzl7/8BZvNxtixY6vuqU/rZvfu3dx9992Eh4cTEBDAFVdcwbffflv1vmVZ/OEPf6BFixYEBASQlpbG5s2bXdjihq2yspKnnnqK+Ph4AgICuOyyy/jzn/9cLQ+U+vTclixZwo033khMTAw2m42ZM2dWe/98+vDQoUMMHz6c4OBgQkNDGT16NMXFxfVqlwKfRmrq1KmMHz+ep59+mu+++45u3boxePBg8vPzXd00t7B48WLS09P5+uuvycjI4Pjx4wwaNIijR49WlRk3bhyzZ89m2rRpLF68mD179jB06FAXttp9ZGVl8X//93907dq12n316YU7fPgwKSkp+Pj4MHfuXLKzs3n55Zdp1qxZVZkXX3yR119/nbfeeovMzEyaNm3K4MGDKSsrc2HLG64XXniBN998k8mTJ7NhwwZeeOEFXnzxRSZNmlRVRn16bkePHqVbt2688cYbtb5/Pn04fPhwfvjhBzIyMpgzZw5LlizhwQcfrF/DLGmUEhMTrfT09KrXlZWVVkxMjDVx4kQXtsp95efnW4C1ePFiy7Is68iRI5aPj481bdq0qjIbNmywAGvlypWuaqZbKCoqstq3b29lZGRYqamp1pgxYyzLUp/W1W9+8xurT58+Z3zf4XBY0dHR1ksvvVR178iRI5afn5/10UcfXYomup0bbrjBGjVqVLV7Q4cOtYYPH25Zlvq0LgBrxowZVa/Ppw+zs7MtwMrKyqoqM3fuXMtms1m7d++uc1s04tMIlZeXs2rVKtLS0qru2e120tLSWLlypQtb5r4KCgoACAsLA2DVqlUcP368Wh937NiR2NhY9fE5pKenc8MNN1TrO1Cf1tVnn31Gz549+cUvfkFkZCTdu3fnH//4R9X727ZtY9++fdX6NSQkhKSkJPXrGfzsZz9j/vz5bNq0CYDvv/+eZcuWcd111wHqU2c4nz5cuXIloaGh9OzZs6pMWloadrudzMzMOtetJKWN0IEDB6isrCQqKqra/aioKDZu3OiiVrkvh8PB2LFjSUlJoUuXLgDs27cPX19fQkNDq5WNiopi3759Lmile/j444/57rvvyMrKqvGe+rRutm7dyptvvsn48eN58sknycrK4rHHHsPX15cRI0ZU9V1tvw/Ur7V74oknKCwspGPHjnh5eVFZWclzzz3H8OHDAdSnTnA+fbhv3z4iIyOrve/t7U1YWFi9+lmBj8g5pKens379epYtW+bqpri1nTt3MmbMGDIyMvD393d1cxoNh8NBz549ef755wHo3r0769ev56233mLEiBEubp17+uSTT/jggw/48MMP6dy5M2vWrGHs2LHExMSoTxsBTXU1QhEREXh5edXYDZOXl0d0dLSLWuWeHnnkEebMmcPChQtp1apV1f3o6GjKy8s5cuRItfLq4zNbtWoV+fn5XHXVVXh7e+Pt7c3ixYt5/fXX8fb2JioqSn1aBy1atCAhIaHavU6dOrFjxw6Aqr7T74Pz9+tf/5onnniCO++8kyuuuIJ77rmHcePGMXHiREB96gzn04fR0dE1NuRUVFRw6NChevWzAp9GyNfXlx49ejB//vyqew6Hg/nz59O7d28Xtsx9WJbFI488wowZM1iwYAHx8fHV3u/Rowc+Pj7V+jgnJ4cdO3aoj89g4MCBrFu3jjVr1lRdPXv2ZPjw4VV/V59euJSUlBpHLWzatIm4uDgA4uPjiY6OrtavhYWFZGZmql/PoKSkBLu9+tejl5cXDocDUJ86w/n0Ye/evTly5AirVq2qKrNgwQIcDgdJSUl1r7zOy6KlQfv4448tPz8/65133rGys7OtBx980AoNDbX27dvn6qa5hV/96ldWSEiItWjRImvv3r1VV0lJSVWZhx56yIqNjbUWLFhgffvtt1bv3r2t3r17u7DV7uf0XV2WpT6ti2+++cby9va2nnvuOWvz5s3WBx98YDVp0sR6//33q8r85S9/sUJDQ61Zs2ZZa9eutW6++WYrPj7eKi0tdWHLG64RI0ZYLVu2tObMmWNt27bN+s9//mNFRERYEyZMqCqjPj23oqIia/Xq1dbq1astwHrllVes1atXW9u3b7cs6/z68Nprr7W6d+9uZWZmWsuWLbPat29vDRs2rF7tUuDTiE2aNMmKjY21fH19rcTEROvrr792dZPcBlDrNWXKlKoypaWl1sMPP2w1a9bMatKkiXXLLbdYe/fudV2j3dBPAx/1ad3Mnj3b6tKli+Xn52d17NjR+vvf/17tfYfDYT311FNWVFSU5efnZw0cONDKyclxUWsbvsLCQmvMmDFWbGys5e/vb7Vt29b63e9+Zx07dqyqjPr03BYuXFjr79ERI0ZYlnV+fXjw4EFr2LBhVmBgoBUcHGyNHDnSKioqqle7bJZ12lGUIiIiIo2Y1viIiIiIx1DgIyIiIh5DgY+IiIh4DAU+IiIi4jEU+IiIiIjHUOAjIiIiHkOBj4iIiHgMBT4iIhdZmzZtaNOmjaubISIo8BERN5Gbm4vNZjvrpeBCRM7F29UNEBG5EJdddhl33313re+FhoZe2saIiNtR4CMibqVdu3Y888wzrm6GiLgpTXWJSKNks9no168fu3btYtiwYURERNCkSRNSUlL46quvav3MgQMHGDt2LPHx8fj5+REZGcntt9/O+vXray1fXl7O3/72N3r16kVQUBCBgYEkJCQwfvx4Dh8+XKN8cXExY8aMISYmBj8/P7p27cr06dNrlCsoKOAPf/gDCQkJBAYGEhwcTLt27RgxYgTbt2+vX8eIeDglKRURt5Cbm0t8fDyDBw9m3rx55yxvs9no2rUrR44coXnz5qSlpbF//36mTp1KWVkZ06dPZ8iQIVXl9+/fT+/evfnxxx/p168fycnJbNu2jenTp+Pn58cXX3xBnz59qsqXlpZyzTXXsHz5ctq3b8+1116Ln58fmzdvJiMjg+XLl3PllVcCZnHz8ePHiYuL4/Dhw6SlpVFSUsLHH39MaWkp8+bNY9CgQQBYlkXv3r3JzMwkJSWFxMRE7HY727dv56uvvmLatGmkpaU5tW9FPIkCHxFxCycDn7Ot8UlOTubaa68FTOADcNddd/H+++9XvV67di29evUiJCSE7du3ExAQAMCoUaOYMmUKv/3tb3n++eernvn5559zww030K5dO3JycrDbzUD5//zP//Dyyy9zzz33MGXKFLy8vKo+U1BQgJeXF4GBgYAJfLZv387NN9/MJ598gq+vLwDz588nLS2tWjC3bt06unbtypAhQ5gxY0a1n+/YsWMcP3686rkiUgeWiIgb2LZtmwWc9RozZkxVecDy8vKycnNzazxr9OjRFmBNnz7dsizLOnbsmOXv72+Fh4dbR48erVH+mmuusQBryZIllmVZ1vHjx62goCArJCTEOnTo0DnbHhcXZwHW1q1ba30vLCys6vXatWstwBo2bNg5nysiF05rfETErQwePBjLsmq9Xn311WplY2NjiYuLq/GMvn37ArB69WoANm7cSFlZGYmJiTRp0qRG+f79+wOwZs2aqvJFRUX06tWLZs2anVe7Q0NDiY+Pr3G/VatWHDlypOp1p06d6Nq1Kx999BFXX301r7zyCt999x0Oh+O86hGRs1PgIyKNVlRU1FnvFxQUAFBYWHjW8i1atKhW7uTnWrZsed5tCQkJqfW+t7d3taDG29ubBQsW8Mgjj7BlyxYef/xxevToQXR0NH/605+orKw87zpFpCYFPiLSaOXl5Z31/slgJDg4+Kzl9+3bV63cyfOCdu/e7bS2ni48PJxJkyaxe/dusrOzmTx5MmFhYTz99NO8+OKLF6VOEU+hwEdEGq0dO3bUuv176dKlAHTv3h2Ajh074u/vT1ZWFiUlJTXKL1q0CKBql9bll19OcHAwWVlZtW5bdxabzUanTp1IT08nIyMDgM8+++yi1SfiCRT4iEijVVlZyZNPPol12ubVtWvX8u9//5vmzZtz/fXXA+Dr68uwYcM4cOAAEydOrPaMefPm8cUXX9CuXTtSUlIAMx31y1/+koKCAsaMGVNj+qmgoIDi4uI6tTk3N5fc3Nwa90+ORvn7+9fpuSJiaDu7iLiF89nODvDEE0/g7+9/1nN8SktL+fTTT2uc45OcnMzWrVsZMGAASUlJ5ObmMm3aNHx9fWuc41NWVsagQYNYunQp7du357rrrsPPz4+tW7cyb948li1bVu0cn5M/w0/169ePxYsXVwVnM2fOZOjQoSQmJpKQkEB0dDS7d+9m5syZFBcXM2PGDG666aZ696eIx3LVdjIRkQtxPtvZAevw4cOWZZnt7KmpqdbOnTutO+64wwoLC7P8/f2t3r17W19++WWtdezfv9967LHHrLi4OMvHx8eKiIiwbrvtNmvdunW1li8rK7P++te/WldeeaUVEBBgBQYGWgkJCdbjjz9e1Q7LMlvW4+Lian1Gamqqdfqv4p07d1pPPPGElZycbEVGRlq+vr5WbGysNXToUGvlypV16jsROUUjPiLSKNlsNlJTU6vW54iIgNb4iIiIiAdR4CMiIiIeQ4GPiIiIeAxvVzdARORi0PJFEamNRnxERETEYyjwEREREY+hwEdEREQ8hgIfERER8RgKfERERMRjKPARERERj6HAR0RERDyGAh8RERHxGAp8RERExGP8P0e3+SZkdZhjAAAAAElFTkSuQmCC\n"
},
"metadata": {}
}
],
"source": [
"import pandas as pd\n",
"\n",
"data = pd.read_csv(f'logs_csv/lightning_logs/version_{csv_logger.version}/metrics.csv')\n",
"fig, ax = plt.subplots(2, figsize=(6,10))\n",
"x = data['epoch'][~data['l2_e_tst'].isnull()]\n",
"y = data['l2_e_tst'][~data['l2_e_tst'].isnull()]\n",
"y2 = data['l2_f_tst'][~data['l2_f_tst'].isnull()]\n",
"ax[0].semilogy(x, y,color='dodgerblue')\n",
"ax[0].set_ylabel('Energy Validation Error (kcal/mol)',size=14)\n",
"ax[1].semilogy(x, y2, label='Force Validation Error (kcal/mol',color='dodgerblue')\n",
"ax[1].set_xlabel('Epochs',size=14)\n",
"ax[1].set_ylabel(r'Force Validation Error (kcal/mol/$\\AA$)',size=14)\n",
"fig.savefig('loss.png', dpi=300)"
]
},
{
"cell_type": "markdown",
"source": [
"### Plotting Training and Validation Loss for $\\Delta$MLP\n",
"\n",
"The loss at each step of the training process is displayed below."
],
"metadata": {
"id": "0TF629ZDMPQ7"
}
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"id": "HCew0e4YnCaG",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 521
},
"outputId": "76721c14-da74-4f82-c7c5-3060b36be958"
},
"outputs": [
{
"output_type": "stream",
"name": "stdout",
"text": [
"315\n",
"100\n"
]
},
{
"output_type": "execute_result",
"data": {
"text/plain": [
""
]
},
"metadata": {},
"execution_count": 17
},
{
"output_type": "display_data",
"data": {
"text/plain": [
""
],
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAiAAAAHFCAYAAADL6EKwAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAACFRklEQVR4nO3dd3hb5d3G8a+8t504Thxn770XYSSMQAaEPQoBwl4Jo0ALtEAYbaEvlFIgzAJpKQXKCCMBQoCQhOw9nb2ns7y3fd4/jo50JMuOp2Q79+e6fMmSjs55ZNHqzu9ZDsMwDERERET8KCjQDRAREZFTjwKIiIiI+J0CiIiIiPidAoiIiIj4nQKIiIiI+J0CiIiIiPidAoiIiIj4nQKIiIiI+F1IoBtQ35SWlnLgwAFiY2NxOByBbo6IiEiDYRgGWVlZpKSkEBRUcY1DAcTLgQMHaNOmTaCbISIi0mDt3buX1q1bV3iMAoiX2NhYwPzjxcXFBbg1IiIiDUdmZiZt2rRxfZdWRAHEi9XtEhcXpwAiIiJSDZUZwqBBqCIiIuJ3CiAiIiLidwogIiIi4ncaAyIi0ggZhkFxcTElJSWBboo0MqGhoQQHB9f4PAogIiKNTGFhIQcPHiQ3NzfQTZFGyOFw0Lp1a2JiYmp0HgUQEZFGpLS0lJ07dxIcHExKSgphYWFaVFFqjWEYHDlyhH379tGlS5caVUIUQEREGpHCwkJKS0tp06YNUVFRgW6ONEJJSUns2rWLoqKiGgUQDUIVEWmETrYMtkh11VZFTf+FioiIiN8pgDhNnTqVnj17MmTIkEA3RUREakH79u15+eWXK338L7/8gsPhID09vc7aJG4KIE6TJk1i48aNLFu2LNBNERE5pTgcjgp/nnrqqWqdd9myZdxxxx2VPv7000/n4MGDxMfHV+t6laWgY9IgVBERCaiDBw+6fv/kk0948skn2bx5s+sx+3RPwzAoKSkhJOTkX19JSUlVakdYWBjJyclVeo1UnyogIiISUMnJya6f+Ph4HA6H6/6mTZuIjY3lu+++Y9CgQYSHh/Prr7+yfft2LrnkElq0aEFMTAxDhgzhxx9/9DivdxeMw+Hgn//8J5dddhlRUVF06dKFr7/+2vW8d2Vi2rRpJCQkMGvWLHr06EFMTAxjxozxCEzFxcXcd999JCQkkJiYyCOPPMLEiRO59NJLq/33OHHiBDfeeCNNmjQhKiqKsWPHsnXrVtfzu3fvZvz48TRp0oTo6Gh69erFt99+63rthAkTSEpKIjIyki5duvD+++9Xuy11SQHED15ZChf8Bz5YG+iWiMipxjAgtygwP4ZRe+/j0Ucf5fnnnyc1NZW+ffuSnZ3NuHHj+Omnn1i1ahVjxoxh/Pjx7Nmzp8LzPP3001x99dWsXbuWcePGMWHCBI4fP17u8bm5ubz44ot88MEHzJs3jz179vDwww+7nv/rX//Khx9+yPvvv8+CBQvIzMzkyy+/rNF7vemmm1i+fDlff/01ixYtwjAMxo0bR1FREWAOGSgoKGDevHmsW7eOv/71r64q0RNPPMHGjRv57rvvSE1N5Y033qBZs2Y1ak9dUReMH6TlwOZjcCQn0C0RkVNNXjH0eD0w1069B6JCa+dczzzzDOeff77rftOmTenXr5/r/rPPPsv06dP5+uuvmTx5crnnuemmm7j22msB+Mtf/sIrr7zC0qVLGTNmjM/ji4qKePPNN+nUqRMAkydP5plnnnE9/+qrr/LYY49x2WWXAfDaa6+5qhHVsXXrVr7++msWLFjA6aefDsCHH35ImzZt+PLLL7nqqqvYs2cPV1xxBX369AGgY8eOrtfv2bOHAQMGMHjwYMCsAtVXqoD4QZjzr1xUGth2iIg0VNYXqiU7O5uHH36YHj16kJCQQExMDKmpqSetgPTt29f1e3R0NHFxcaSlpZV7fFRUlCt8ALRs2dJ1fEZGBocPH2bo0KGu54ODgxk0aFCV3ptdamoqISEhDBs2zPVYYmIi3bp1IzU1FYD77ruPP/3pT5xxxhlMmTKFtWvd5fW7776bjz/+mP79+/P73/+ehQsXVrstdU0VED8IdS4UpwAiIv4WGWJWIgJ17doSHR3tcf/hhx9m9uzZvPjii3Tu3JnIyEiuvPJKCgsLKzxPaKhnScbhcFBaWv7/Ofs63qjNvqVquO222xg9ejQzZ87khx9+4LnnnuNvf/sb9957L2PHjmX37t18++23zJ49m/POO49Jkybx4osvBrTNvqgC4gchVgVEm1KKiJ85HGY3SCB+6nILmgULFnDTTTdx2WWX0adPH5KTk9m1a1fdXdCH+Ph4WrRo4bF8Q0lJCStXrqz2OXv06EFxcTFLlixxPXbs2DE2b95Mz549XY+1adOGu+66iy+++IKHHnqId955x/VcUlISEydO5D//+Q8vv/wyb7/9drXbU5dUAfGDMGcFpFgVEBGRWtGlSxe++OILxo8fj8Ph4IknnqiwklFX7r33Xp577jk6d+5M9+7defXVVzlx4kSllitft24dsbGxrvsOh4N+/fpxySWXcPvtt/PWW28RGxvLo48+SqtWrbjkkksAeOCBBxg7dixdu3blxIkTzJkzhx49egDw5JNPMmjQIHr16kVBQQEzZsxwPVffKID4gVUBKVQFRESkVrz00kvccsstnH766TRr1oxHHnmEzMxMv7fjkUce4dChQ9x4440EBwdzxx13MHr06Ept0jZixAiP+8HBwRQXF/P+++9z//33c9FFF1FYWMiIESP49ttvXd1BJSUlTJo0iX379hEXF8eYMWP4+9//DphrmTz22GPs2rWLyMhIzjrrLD7++OPaf+O1wGEEujOrnsnMzCQ+Pp6MjAzi4uJq5Zxvr4Q/z4fLusPLo2vllCIiPuXn57Nz5046dOhAREREoJtzyiktLaVHjx5cffXVPPvss4FuTp2o6L+xqnyHqgLiB6HOCoi6YEREGpfdu3fzww8/MHLkSAoKCnjttdfYuXMn1113XaCbVu9pEKofhKoLRkSkUQoKCmLatGkMGTKEM844g3Xr1vHjjz/W23EX9YkqIH4QqkGoIiKNUps2bViwYEGgm9EgqQLiB6GahisiIuJBAcQPtBCZiIiIJwUQP9BCZCIiIp4UQPxAe8GIiIh4UgDxgxB1wYiIiHhQAPEDDUIVERHxpADiB1qITESk7p199tk88MADrvvt27fn5ZdfrvA1DoeDL7/8ssbXrq3znEoUQPzANQtGFRARkTLGjx/PmDFjfD43f/58HA4Ha9eurfJ5ly1bxh133FHT5nl46qmn6N+/f5nHDx48yNixY2v1Wt6mTZtGQkJCnV7DnxRA/EDTcEVEynfrrbcye/Zs9u3bV+a5999/n8GDB9O3b98qnzcpKYmoqKjaaOJJJScnEx4e7pdrNRYKIH4QqlkwIiLluuiii0hKSmLatGkej2dnZ/Ppp59y6623cuzYMa699lpatWpFVFQUffr04aOPPqrwvN5dMFu3bmXEiBFERETQs2dPZs+eXeY1jzzyCF27diUqKoqOHTvyxBNPUFRUBJgViKeffpo1a9bgcDhwOByuNnt3waxbt45zzz2XyMhIEhMTueOOO8jOznY9f9NNN3HppZfy4osv0rJlSxITE5k0aZLrWtWxZ88eLrnkEmJiYoiLi+Pqq6/m8OHDrufXrFnDOeecQ2xsLHFxcQwaNIjly5cD5p4248ePp0mTJkRHR9OrVy++/fbbarelMrQUux9oEKqIBIphGOTm5gbk2lFRUTgcjpMeFxISwo033si0adP44x//6HrNp59+SklJCddeey3Z2dkMGjSIRx55hLi4OGbOnMkNN9xAp06dGDp06EmvUVpayuWXX06LFi1YsmQJGRkZHuNFLLGxsUybNo2UlBTWrVvH7bffTmxsLL///e+55pprWL9+Pd9//z0//vgjAPHx8WXOkZOTw+jRoxk+fDjLli0jLS2N2267jcmTJ3uErDlz5tCyZUvmzJnDtm3buOaaa+jfvz+33377Sd+Pr/dnhY+5c+dSXFzMpEmTuOaaa/jll18AmDBhAgMGDOCNN94gODiY1atXExoaCsCkSZMoLCxk3rx5REdHs3HjRmJiYqrcjioxxDAMw3jttdeMHj16GF27djUAIyMjo9bOvSfDMNq+bBhdX6u1U4qI+JSXl2ds3LjRyMvLMwzDMLKzsw0gID/Z2dmVbndqaqoBGHPmzHE9dtZZZxnXX399ua+58MILjYceesh1f+TIkcb999/vut+uXTvj73//u2EYhjFr1iwjJCTE2L9/v+v57777zgCM6dOnl3uNF154wRg0aJDr/pQpU4x+/fqVOc5+nrffftto0qSJx/ufOXOmERQUZBw6dMgwDMOYOHGi0a5dO6O4uNh1zFVXXWVcc8015bbl/fffN+Lj430+98MPPxjBwcHGnj17XI9t2LDBAIylS5cahmEYsbGxxrRp03y+vk+fPsZTTz1V7rXtvP8bs8vIyKj0d6i6YJwmTZrExo0bWbZsWa2fO0wVEBGRCnXv3p3TTz+d9957D4Bt27Yxf/58br31VgBKSkp49tln6dOnD02bNiUmJoZZs2axZ8+eSp0/NTWVNm3akJKS4nps+PDhZY775JNPOOOMM0hOTiYmJobHH3+80tewX6tfv35ER0e7HjvjjDMoLS1l8+bNrsd69epFcHCw637Lli1JS0ur0rXs12zTpg1t2rRxPdazZ08SEhJITU0F4MEHH+S2225j1KhRPP/882zfvt117H333cef/vQnzjjjDKZMmVKtQb9VpQDiB9ZS7CUGlBqBbYuInFqioqLIzs4OyE9VB4DeeuutfP7552RlZfH+++/TqVMnRo4cCcALL7zAP/7xDx555BHmzJnD6tWrGT16NIWFhbX2t1q0aBETJkxg3LhxzJgxg1WrVvHHP/6xVq9hZ3V/WBwOB6WldTdY8KmnnmLDhg1ceOGF/Pzzz/Ts2ZPp06cDcNttt7Fjxw5uuOEG1q1bx+DBg3n11VfrrC2gMSB+EeoOuBSVQLj+6iLiJw6Hw+Nf4vXZ1Vdfzf33389///tf/v3vf3P33Xe7xoMsWLCASy65hOuvvx4wxzxs2bKFnj17VurcPXr0YO/evRw8eJCWLVsCsHjxYo9jFi5cSLt27fjjH//oemz37t0ex4SFhVFSUnE5u0ePHkybNo2cnBzX337BggUEBQXRrVu3SrW3qqz3t3fvXlcVZOPGjaSnp3v8jbp27UrXrl357W9/y7XXXsv777/PZZddBkCbNm246667uOuuu3jsscd45513uPfee+ukvaAKiF+E2v7KWoxMRMS3mJgYrrnmGh577DEOHjzITTfd5HquS5cuzJ49m4ULF5Kamsqdd97pMcPjZEaNGkXXrl2ZOHEia9asYf78+R5Bw7rGnj17+Pjjj9m+fTuvvPKKq0Jgad++PTt37mT16tUcPXqUgoKCMteaMGECERERTJw4kfXr1zNnzhzuvfdebrjhBlq0aFG1P4qXkpISVq9e7fGTmprKqFGj6NOnDxMmTGDlypUsXbqUG2+8kZEjRzJ48GDy8vKYPHkyv/zyC7t372bBggUsW7aMHj16APDAAw8wa9Ysdu7cycqVK5kzZ47rubqiAOIHHhUQBRARkXLdeuutnDhxgtGjR3uM13j88ccZOHAgo0eP5uyzzyY5OZlLL7200ucNCgpi+vTp5OXlMXToUG677Tb+/Oc/exxz8cUX89vf/pbJkyfTv39/Fi5cyBNPPOFxzBVXXMGYMWM455xzSEpK8jkVOCoqilmzZnH8+HGGDBnClVdeyXnnncdrr71WtT+GD9nZ2QwYMMDjZ/z48TgcDr766iuaNGnCiBEjGDVqFB07duSTTz4BIDg4mGPHjnHjjTfStWtXrr76asaOHcvTTz8NmMFm0qRJ9OjRgzFjxtC1a1def/31Gre3Ig7DMDQqwSYzM5P4+HgyMjKIi4urlXMaBnR4xRwWvuw2aN4wqqEi0gDl5+ezc+dOOnToQERERKCbI41QRf+NVeU7VBUQP3A43FUQdcGIiIgogPiNFiMTERFxUwDxkxAtxy4iIuKiAOInYdoRV0RExEUBxE+sCojGgIiIiCiA+I01CLVQAURE/EATHKWu1NZ/WwogfqJBqCLiD9by3oHaAVcaP2tpevs+NtWhRcH9JFRdMCLiB8HBwSQkJLg2NYuKinItZy5SU6WlpRw5coSoqChCQmoWIRRA/MTVBaMKiIjUseTkZIBq76wqUpGgoCDatm1b42CrAOInGoQqIv7icDho2bIlzZs3p6ioKNDNkUYmLCyMoKCaj+BQAPET1zRcBRAR8ZPg4OAa99OL1BUNQvWTEA1CFRERcVEA8ZNQrYQqIiLiogDiJ6FaCVVERMRFAcRPVAERERFxUwDxE1VARERE3BRA/EQLkYmIiLgpgPiJ9oIRERFxUwDxE9dCZOqCERERUQDxl7hw8/aI9ocSERFRAPGXXknm7YYjgW2HiIhIfaAA4ie9nQFk01HNhBEREVEA8ZO28RAXBgUlsPV4oFsjIiISWAogfuJwQM/m5u/rtUO2iIic4hRA/KhXM/N209HAtkNERCTQFED8qF2CebsvK6DNEBERCTgFED9qHWfe7ssMbDtEREQCTQHEj1rHmrcKICIicqpTAHGaOnUqPXv2ZMiQIXV2jVbOCkhGAWQW1NllRERE6j0FEKdJkyaxceNGli1bVmfXiAmDJhHm7/tVBRERkVOYAoifWeNA9msgqoiInMIUQPyslXMcyF5VQERE5BSmAOJnmgkjIiKiAOJ3CiAiIiIKIH637rt/cvjVkSz86p1AN0VERCRgFED8rPDEPgq2z+NA6pJAN0VERCRgFED8bNiA3gBk71tPdmGAGyMiIhIgCiB+NsQZQIoObWBvemmAWyMiIhIYCiB+1rlzZxwhYRgF2axI3R3o5oiIiASEAoifhYSE0KRNDwCWr1kf4NaIiIgEhgJIALTuZHbDbNigACIiIqcmBZAA6NTdDCC7tyiAiIjIqUkBJAB69zYDSNpOBRARETk1KYAEwKD+ZgDJ3L+JoqKiALdGRETE/xRAAqB/t7Y4wmMwigvZunVboJsjIiLidwogAdAyNojQ5F4AvDZzPRkFAW6QiIiInymABEBYMMS26QPAhz+t55m5AW6QiIiInymABEhSB+eKqAfX88MOKCoJcINERET8SAEkQFp1cgeQzAJYdiDADRIREfEjBZAAyW9qBpDio9soLczjxx0BbpCIiIgfKYAEyIiezQmKbgZGKcVpm/hxJxhGoFslIiLiHwogAfKHsxx06mZWQYzD69mdAVuPB7hRIiIifqIAEiAxYTD6dDOANMs2V0RVN4yIiJwqFEACyFqS3ZG2DoA1hwPZGhEREf9RAAkgK4Ac2mFWQLILA9kaERER/1EACaBevczVUI8e3EtpXoYCiIiInDIUQAIoISGB1q1bA1B0aAPZ2pdOREROEQogAWZ1wxQdXK8KiIiInDIUQALMCiCFB9eRowAiIiKnCAWQAOvfvz8AhftWkl2oxchEROTUoAASYEOHDgWgaN9KSkuKyNU4EBEROQUogARY586dadKkCUZRPkUH1mogqoiInBIUQALM4XC4qiAFu5dqHIiIiJwSFEDqgWHDhgFQuHuJZsKIiMgpQQGkHnBXQBRARETk1KAAUg9YAaQ4bRNpxzMC3BoREZG6pwBSDyQlJRHToiMAq1YsC3BrRERE6p4CSD3RoptZBdm4akmAWyIiIlL3FEDqiTY9zIGovy5eypGcADdGRESkjimA1BPte5sVkLTNS7j3Oy2HKiIijZsCSD3RuecACAqhNOsw89ftCXRzRERE6pQCSD0RFhFJWKt+ABTuWcrR3AA3SEREpA4pgNQTmQUQ1ta9HkjqkQA3SEREpA4pgNQTdw6Ctr3cK6JuOBrgBomIiNQhBZB6onUcfP5bZwDZu4L1h4oD3CIREZG6owBSj3Tt2pXo2HiMojyWr14f6OaIiIjUGQWQeiQoKIhBg4cAsG3tEvJVBBERkUZKAcRp6tSp9OzZkyFDhgS0HWecZg5Ezd+1hC3HAtoUERGROqMA4jRp0iQ2btzIsmWB3YvltNOscSDL2aCZMCIi0kgpgNQzgwcPBqDo0AbW7NWa7CIi0jgpgNQzKSkpNElqCUYpPy9ajaFV2UVEpBFSAKmHThtmjkPZun45aw4HuDEiIiJ1QAGkHho+1OyGKdyzjI83BLgxIiIidUABpB6yxoEU7l3OurQAN0ZERKQOKIDUQ1YAKU7bzIn0zAC3RkREpPYpgNRDSUlJtGrTDoC0rSsD3BoREZHapwBST/UfaFZBjm9fppkwIiLS6CiA1FNDh5gBpGDPcnKLAtwYERGRWqYAUk+d7pyKW7h3OZkFAW6MiIhILVMAqacGDRoIQPGxHew+qE1hRESkcVEAqaeaNGlCRPPOACxbviLArREREaldCiD1WNNO5jiQ1SuXB7glIiIitUsBpB5r0dUcB7J+dWB36BUREaltCiD1WJseZgVk63pVQEREpHFRAKnHOvQYAA4HJw7v49ChQ4FujoiISK1RAKnHkprEEtK8OwArVmggqoiINB4KIPVYXDiEtzXHgSxbpnEgIiLSeCiA1GNx4RDWxhwHogAiIiKNiQJIPWYPICtWrMDQpjAiItJIKIDUY/HhENqqHziCOHz4MAcOHAh0k0RERGqFAkg91i4BgsKiCEvuCWggqoiINB4KIPVY2zgIDYLQ1oMAzwDy807YcCRQLRMREakZBZB6LDTYrIKEtfEMIHsy4Oav4a6ZAWyciIhIDSiA1HOdm5QNIOvSzOeO5QaqVSIiIjWjAFLPdW4Koa364wgK4tChQ+zdd4Ctx8znCksC2zYREZHqUgCp5zo1NQeiRrbsAcCtb61gy3HzuaJSKNXMXBERaYAUQOq5Lk3MW0eK2Q2zZNkKthxzP68qiIiINEQKIPVcR2cACXPOhCnct4IdJ9zPK4CIiEhDpABSz0WHQUqMeyBq0d4VlNi6XRRARESkIVIAaQCsgag4gijJPEhJxkHXcwogIiLSECmANAAdm0BQeDShLboDZjeMRQFEREQaIgWQBiA6zLy1VkQt3KsAIiIiDZsCSANwemvz1hoHYg8gBQogIiLSACmANABntoU3xsG157tnwoQHm8+pAiIiIg2RAkgDMa4LXHFuf3A4KMk4QFLpIUABREREGiYFkAbkjE4xxLUyB6Lm7zG7YRRARESkIVIAaUAiQuDis81umJzdZgA5nA3LD8DifXAiL5CtExERqTwFkAZm0CAzgGTuMgPI736EKz6Faz6HCz8CQ3vDiIhIA6AA0sAMHjwYgPTtyzCcacPhfG5/FuQWBahhIiIiVaAA0sAMGjSI0NBQ8k4cpPjYDgBaxECwM4VkFQawcSIiIpWkANLAREZGMnToUAAKts0FIDoUYpyLlSmAiIhIQ6AA0gCNHDkSgILt8wAzgMSGm89lFQSqVSIiIpWnANIAjRgxAoD87WYFJCoMYp0VkGxVQEREpAFQAGmATj/9dBxBwZQc30XxiT1EhbgDiLpgRESkIVAAaYBiY2Np2XUgYHbDRIepC0ZERBoWBZAGqmN/cxxI/vZ5RGkQqoiINDAKIA1Ul4HmOJCCbXPNQahWAFEFREREGgAFkAaq64AzweGg+MgWSjIPaRCqiIg0KAogDVRCkyaEtuwLwP5181xjQDIVQEREpAFQAGmgwoMhvLM5DmTX2nmuMSCqgIiISENQowCyd+9efv75Z3Jzc12PlZaW8te//pUzzjiDUaNGMXPmzBo3UsoKC4aITuY4kK0r52oWjIiINCghNXnxE088wTfffMOhQ4dcj/35z39mypQprvtz585l4cKFDBkypCaXEi9hwRDuDCB7t67HyD4KNFMFREREGoQaVUAWLFjAqFGjCA0NBcAwDF577TW6d+/Onj17WLp0KdHR0bzwwgu10lhxCwuG4JgkQlr0AGDb6l8BTcMVEZGGoUYBJC0tjXbt2rnur169miNHjnDvvffSunVrBg8ezKWXXsqyZctq3FDxFBZs3kZ0MseBbFhuLsueqS4YERFpAGoUQEpLSyktLXXd/+WXX3A4HJx77rmux1q1auXRRSO1wwogVjfMqsXmxnTqghERkYagRgGkbdu2LF261HX/yy+/pGXLlnTr1s312KFDh0hISKjJZcSHcCuAOGfCbFi7iqIj28grhqKSADZMRESkEmoUQK644goWLFjAlVdeyfXXX8+vv/7KFVdc4XHMxo0b6dixY40aKWVZFZCQ+BTOvWAshmGQ8+tUAI7nB7BhIiIilVCjAPLwww8zZMgQvvjiC/773//Sp08fnnrqKdfzu3fvZunSpZx99tk1bKZUZNLk+wDIXvIepflZHMkJcINEREROokbTcOPi4li8eDHr168HoEePHgQHB3sc88UXXzB48OCaXEZ8KHIPvWH82Avo2rUrW7ZsIWfZvzl6zaTANUxERKQSamUl1N69e9O7d+8y4aNdu3ZccskltGrVqjYuIzaG4f49NCSIe++9F4Csea+Qll1azqtERETqhxoFkKysLHbs2EFRUZHH45988gkTJkzgtttuY9WqVTVqoPg2tBX0bAaXdTfvT5w4kbCoOIqPbGHezz8EtnEiIiIn4TAM+7+lq+buu+/mP//5D4cPHyYqKgqAN954g8mTJ2OdNjIykhUrVtC9e/faaXEdy8zMJD4+noyMDOLi4gLdnAoZBjgc7vtnXP1bFn76Ml2GjWXL4m8D1zARETklVeU7tEYVkLlz5zJq1ChX+AB4/vnnadWqFfPmzeN///sfhmFoJdQ6Yg8fAGMnTAKHg61LvmPLli2BaZSIiEgl1CiAHDx4kA4dOrjup6amsnfvXu677z7OPPNMrrzySi6++GLmzZtX44bKyfXs1pmInhcC8NprrwW4NSIiIuWrUQApKCggLCzMdX/u3Lk4HA4uuOAC12MdO3Zk//79NbmMVFLzKIgdYU7Jff/998nIyAhwi0RERHyrUQBp3bo1a9eudd2fMWMGTZs2pW/fvq7Hjh07RkxMTE0uI5XULAoiuo4iPLkH2dnZTJs2LdBNEhER8alGAWTs2LH88MMPPPzwwzz++ON8//33jB8/3uOYLVu20LZt2xo1UiqnWRQ4HA6izjKrIK+++qrHXj0iIiL1RY0CyGOPPUbbtm156aWX+Mtf/kKLFi145plnXM+npaWxYMECRowYUeOGysk1jYTYMIgefAMxsXFs376duXPnBrpZIiIiZdQogCQnJ7Nhwwa+/vprvv76a1JTU2ndurXr+aNHj/LCCy9wxx131LihcnJBDujdHILCoxk6+hoA/v3vfwe4VSIiImXVaB2QxqghrQPiy19+hbdWwEh+5YMHziImJoZDhw4RHR0d6KaJiEgjV5Xv0BrtBWO3f/9+Vq9eTWZmJnFxcfTv319LsAdA3+bm7YnmZ9ChQwd27tzJl19+yYQJEwLbMBEREZsa7wWzbds2zj//fNq2bcvFF1/M9ddfz8UXX0zbtm254IIL2LZtW220UyqpbwvzdtMxB5dcfSOgbhgREal/atQFs3fvXoYMGUJaWhrdu3dnxIgRtGzZkkOHDjFv3jxSU1Np0aIFS5cupU2bNrXZ7jrT0LtgDAMu+hjWp0Hzgh0sf6QTQUFBbN2xh47tVJESEZG647el2J9++mnS0tJ4/fXX2bBhA2+++SZTpkzhjTfeYMOGDbzxxhscPnzYY2aM1C2HA94bD23jIS28I1GdzqS0tJQRD/6XrIJAt05ERMRUowAya9Ysxo8fz1133YXDe2MS4M4772T8+PF89913NblMtVx22WU0adKEK6+80u/XDrQWMfDfyyElBiIGm90waQv/RepRjTcWEZH6oUYBJC0tjd69e1d4TO/evTly5EhNLlMt999//yk99qFNHEy/Bs4ccxWEhFN0aAO/LlkNQFEJnMhzH7vtOPxnLZRozTIREfGTGgWQpKQkNm7cWOExGzduJCkpqSaXqZazzz6b2NhYv1+3PkmOga9uSqDL6ZcAMONTM5Dd/S0MfRf2ZZrHPfkL/HEO/Lizetc5ngeP/AhrDtVCo0VE5JRQowAyevRovv76a959912fz7/33nt88803jBkzpkrnnTdvHuPHjyclJQWHw8GXX35Z5pipU6fSvn17IiIiGDZsGEuXLq3OWzglnDXe7IZZ8v2HFBUVsfYwFJbAamdg2J1u3m5Iq975754JH2+AO2fWvK0iInJqqFEAmTJlComJidxxxx306dOHyZMn8+yzzzJ58mT69u3L7bffTtOmTZkyZUqVzpuTk0O/fv2YOnWqz+c/+eQTHnzwQaZMmcLKlSvp168fo0ePJi2tmt+gjdzZ511AUGwLctOP8Pnnn5Oebz6+OwNKDTiUY97fdKx651/s3Oz4YHbN2yoiIqeGGi1E1rZtWxYsWMCdd97JL7/8woYNGzyeP+ecc3jzzTerPAV37NixjB07ttznX3rpJW6//XZuvvlmAN58801mzpzJe++9x6OPPlqlaxUUFFBQ4J4ekpmZWaXXNwTtm4YSe+YkMr57kr/+9f/In3gNDoeDPRlwNBeKnWM/tlQjgFhhBqBTk9ppr4iINH41XoisS5cu/Pzzz+zevZuvvvqKDz74gK+++ordu3fz008/8cUXX3DeeefVRlsBKCwsZMWKFYwaNcr1WFBQEKNGjWLRokVVPt9zzz1HfHy866ehrFdSFSlxEHPmPTjColi9ehUFW38GzArIIVvVYlc65BdX7dwL9rp/j4+oeVtFROTUUGtLsbdp08bnl/emTZv45ZdfausyHD16lJKSElq0aOHxeIsWLdi0aZPr/qhRo1izZg05OTm0bt2aTz/9lOHDh5c532OPPcaDDz7oup+ZmdnoQkirWAiOTiR62K1kz3+VzJ/+j4iu57Enw7PbxAC2Hoc+zSt/7r22glFVw4uIiJy6ai2A1Dc//vhjpY4LDw8nPDy8jlsTWBEh0CwSis9+kNyFr5O/+QcK96/hQKt+7MnwPHbLsaoFkIJi37+LiIhUpMZdMP7WrFkzgoODOXz4sMfjhw8fJjk5OUCtqv9axUFIYnu6nHUVAJk/v4ABLD/gedzmKo4DKSix/a4AIiIildTgAkhYWBiDBg3ip59+cj1WWlrKTz/95LOLRUwpziVREkf9DoDcVR9TfHw3S5wzWNrGm7ebj1btvPbQoS4YERGprHoZQLKzs1m9ejWrV68GYOfOnaxevZo9e/YA8OCDD/LOO+/wr3/9i9TUVO6++25ycnJcs2KkrFbOALI/ZiDhXc+D0hKy5r7MCecslpHtzFv7TJhl++G2bzzHeXizV0DyS8o/TkRExK5ejgFZvnw555xzjuu+NUh04sSJTJs2jWuuuYYjR47w5JNPcujQIfr378/3339fZmCquLV2bkpoAHHn/p4jW34ie9E7xF3wOMHRiZzfET5YCweyIbMA4sLhys/M16Tnw2dX+T6vKiAiIlIdVQ4g48aNq9Lx69atq+olOPvsszGMijdOmzx5MpMnT67yuU9VrWyr0kd0O5/INgPI27uKjBl/oOk1bzGoJbSMMWfFbD4GQ1Lcx1fULWOvgBSXmj8h9bKuJiIi9UmVA8j3339f5Yv42ilX/CvFFkAcDgdn3fkyPzw+kuxFb9P+7InEhJ1O56ZmANmV7hlACiroWvEeeJpfDDFhtdp0ERFphKocQHburOaOZRJQVheM5fxzR7Bg6M3kLH2fff+9i6KnV9A0MhTwXN0UzH1jyuMdThRARESkMqocQNq1a1cX7ZA6Fh8O0aGQU2Te79kMEi7+P/I2fE367nW8/PLLNBlizpA54RVAKuoM81UBERERORn11p8iHA64sIv7fvNoCI5pRsLFLwDw1FNPUXpiNwAZ+b7O4JuvCoiIiMjJKIA4TZ06lZ49ezJkyJBAN6XOPH8ePHoGXN0T+ifDg6dBnwtuYvgZI8jNzWXGy/diGAbp+WWDRHndMAogIiJSHQogTpMmTWLjxo0sW7Ys0E2pM8FBcPdgeOF8c6bK/cPgl5sc/PPtNwgNDWX1vG/I+uXvpOebU3HtjuWat96Tk9QFIyIi1aEAIvTs2ZNnnnkGgPSvHmLlFy+R4RVAjuTC7B0w8B34yTYOWRUQERGpDgUQAeCRRx7h9t8+AcCmDx/i9X/8zeP5I7nmqqjH8+CWr92PWxUQa+0P7QcjIiKVoQAigLk2yGNPPEPc6CkAvPzMw2T+/ILr+aO5vl9nVUDinRsK55fAngw44314Z2VdtlhERBoyBRBxaRIJCWOfIn7MUwCkf/17Mn/8K1BBAHFWPFwBpBj+8ivsy4Q/za/jBouISIOlACIusWHgAOLHTGH0bU8DkD7jUTJmPVtmUGpGgTkg1VUBiTBv84vhcI7/2iwiIg2TAoi4BAeZm9AB9LjySeIv/DMAGd89yRevP+mxP8/NX8H2E1DqfCjOVgHJLqx5W0oNKCmt+XlERKR+UgARDwnOSsaeDIg//w8kXmKOA1n+0bNkzPiDK4SsOAgvLHS/zt4Fk+VVLakqw4ArP4XzPoCiCpaBFxGRhksBRDw0sQJIpnnb57KHSbj07wBk/vQ8xz++DaPIXCp1wV7368qrgFRnWm6JYQacnemw7XjVXy8iIvWfAoh4sMZypDnHcbSOg7izH6DJlVPBEUTOkvc4/OpIitP3u/aVCQ8G5z52ZBd6BhDv9UQqw171qGgnXhERabgUQMSD1ZViaePcRTf2zHtIuvM7ImKbULhnKYf+Nojc7b8CZgCJcG5ruCvdc/O6quwrYylUABERafQUQMRDnFcAaR3n/j2y+wX8btoy+vTpQ2nWYdJeO4eM758mtCSXiGDzmC1eXSbes2cqwx5A8oqq/noREan/FEDEg9UFY2kT73m/b/dOLFq0iDanXwOlxWR8/xQbnuzGmtn/xTAM9mV6Hl+tLhjb7JccBRARkUZJAUQ8eFdA2sR53k+OgejoaCY8/RGJEz8huEk7Ck/s45+PT+Dwy6dTsGsJA1u6B7PWtAJS0xk1IiJSPymAOE2dOpWePXsyZMiQQDcloLzHgDSPhrBg9/2UWPO2Y1MH0QOupuVjqXS56s9ER0dTuHsxh18+jWaz72Bg0yygahWQR3+Cp+d6BpDy1hR5ZSmM+2/1Ao6IiASeAojTpEmT2LhxI8uWLQt0UwLKuwISHw5xYe77LWPM245NzNugsEh6XP4HtmzZwk033QTAP//5Dl/c14/87fMrHRCO5cJH6+G91Z6horwA8vF62HDEnK5bV7Yc0+6+IiJ1RQFEPNgrIMEOiAp1jwtJiHBPt+3UxH1ceAikpKTw/vvvM2fOHNq1a0fGoZ2kvTaS//39d+Tnn3wqjD1oHM9z/57lI4AYhrk7r/extWnlQTj/P/D7H+vm/CIipzoFEPFgDyBx4eBwuKsiVvUDzNkxoc7/esJtXTRnn302a9eu5bTxt4BhsODjFxk8eDArV1a8NW62bbDpMVuo8FUBySxwd9Mcq6MAknrUvN2dXjfnFxE51SmAiIe48LK/+wogIUHQLsH8PTzE6xxxcdz97Ls0u+1rIhOas2HDBoYNG8YzzzxDUZHvaS05tqBxzLbzrj2AvLwYbpgO+7Pcjx0vZ5femjriXIhNXTAiInVDAUQ82KfhRju7W6yqiDUA1WJ1w9grIPbzRPUezwV/28D4y66kuLiYKVOmcPrpp5Oamlrm+Mp0wfx9CczbA/9a436sriogVhePAoiISN1QABEPMWFlH7PWAunc1PPxDgnmrXcFBKCVM6wcKG3G6Q/+j8QbPsQRmcDy5csZMGAAL774IiUl7ukuOVXogtlxwv17XY0BcQUQrcQqIlInFEDEQ4iP/yImDYb3xsN1vT0fv7Qb9GkOF3ct+5puiebt4RzYn+UgetB1tHxkPWPGjKGgoIDf/e53jBw5kq1btwLlV0B8BZADti6YuqqApKkLRkSkTimAyElFh8F5HctWOnokwYxr4ez2ZV8TG+5exGzVIfM2JKEV3377Le+88w6xsbEsWLCAfv368corr5CV717+9KiPAGLfoM5jDIi6YEREGiQFECmXcfJDKtSjmXm717Y8e6nh4LbbbmPdunWce+655OXlcf/99/P8rSMoOrwZ8D0GJM8WBOztqosAYhieg1CNmv4hRESkDAUQqTPdm5V9zBrr0a5dO2bPns3UqVOJiYlh59oFHHyhH5k//pVj2e60kV1oBoDyKhFZhVBQy1WKrELPXXi1I6+ISO1TAJFy9W5es9f7DCC2MR1BQUHcc889rF+/ng6DR0NxAekzHmXPi8Mo3LsCgFIDcosq7go5cfJ1zqrkiNfU3toOOCfz0w64fjocyvbvdUVE/EkBRMqYcS3c0h+eOKtm5+nhI4Bk+1gGJKFFO8578juaXjcNR2QCRftWcuiloZz44gFK87PIKqw4gNT2QFRrAKolz88B5JZvYP4emPStf68rIuJPCiBSRp/mMGWk55og1dEuHiK8Bq7meM1q2XkCzpoGP+xwEDN0Iil/2ETUoOvAKCVr3j84+FwPPvnfZ+QWluKtebR5W9nFyEpKYfUh87YiR7wCSKAGoi6vw31uREQCTQFE6kxwEHT1WjvEPq22qAQemOW5Y25wbAua3fAhSXfNIqRZJ0oy9vPArVdx1bn9yVn5MUapOSAjNMi9IV55FZBD2fDBWrMLB+C5BXDJJ54Lmfni3QXj7wCSYAt+/u7+ERHxFwUQqVPe40DsC469uhRWH/b9usjuF5D8+3XEjX6SyOhYtm1ax7F/X8vB53qSveR9moYV0SzSPLa8mTDXfg6Pz4HnfjXvv+PcjubZ+RW3OdAVkNZx7t/XlPP3ERFp6BRAnKZOnUrPnj0ZMmRIoJvSqHiPA7G6YHalw2vLzN/jfKy+ChAUFknC2Kd5edZubnjgGYKimlJ8ZAvHP7qFtY+1Z8lb95C38TsOpZujULefMKsb1kZ1O9LN2++2eXb92L/gfQl0BaTQNuvG2hRPRKSxUQBxmjRpEhs3bmTZsmWBbkqjMiTF877VBfPvtVBiwMh2MLpTxecoDG3CFXc9QcqU3SRc8iJBcckUnDjAiq/f4Mjb43hqXCJXXnkl9/xzFU/+Ag/94Pn6olJYUYXxFIEOIPZul1zfe/eJiDR4CiBSp/q0gG9+A+d3NO/nFEFeEXy6wbx/c39om1DxOU7kmyEgKDyGuHMeotUTO7nyTzM456q7CI5vRVF+Lp9//jk//H4gRz+4ni8W7fLolikqgSX73fcPZpnTe8sT6C4YewUkRwFERBopBRCpc31buHfSzS6EZQcgsxBSYswKSNtyukSswZjp+Z5TYR2hEQw/90Ie+vMbpDy1l/P+upLrrrsOgNwVH3LgL9244a6HKMk+ApgVEGs5eOu+d8iwsyog1vX9XgGxBZBcH3vhiIg0Bgog4hfWLrs5Re7ukGGtIcjhnk4LEB7s/r2F83GrAmKXFA1NI8HhcFCaPIAPP/yQQU8tJ7zLuVBSyLf/fokDz3Qg/ZvHyMs8xjqvwZz7svCppNQ9q8bayyaQXTCqgIhIY6UAIn4RE2reZhfC8gPm74Namrf2gapJUe7fm9sCiPd01KQoSHTOgrECQ2jrQTS/50eS7vyOZp0GYhTmkPnT8xx4pj17pj9OaP4xBjqvuT8Tn47lmd0zQQ5o5aza5Pt5KXZ7F4zGgIhIY6UAIn4R7ayAZBa4u0OsANIkEmZfD/MmmrvoWqwAkp5XtgqREmtWQMDsoikuNbtpHA4HkT3G0PPx5TS79UtCW/XHKMgmc/af2TWlLbs+/i3F6fs4UE4FxFoFNTHS3ebKVEB+2eUOVjVRUmp2EVkUQESksVIAEb+wumAW7jW7FWLCoFui+/muidAuAWJtU3KbO6shx21jQHolwUPDzdVam0SAw3nsiTzPcSK7MhxE9bmE5IdX0uyWLwhtPZCSglxWT3+ZA8925K0pt7Jp06Yy7bTGfyRFQ4SzOyizAH43G2Zu9f3eMvLhlq/hpq/MIFQThV7VFnXBiEhjpQAifhHt7ILJcg6qvGOguVKqN3sFpEWMeZuR764EjOkM9w0Fh8N8vTVQ9JiPKgmYFZGovpeR/NByprzzPV0GjoSSIlZ/+x49e/ak39mXMfOnRa7jrcGpSVHuZeTn74b/bYT/W+D7vR3OMacUZxXCwWyzHdUdN+IdQFQBEZHGSgFE/CLGVtkY39UMEb54VECcXTAGcNi5M6z33jJWN8x+W5eKNTbEzuFwcNOVo3nmX7/Q4v6FtBl6MYZhsHbul1w06nRGjBjBt99+S1qOOT+3uS2AHHaGkj2ZZQMCeC4lv+sEjP4PDHwbpi4Do4Lpvr54jzdRBUREGisFEPGLbolmuDitFbx4vlnB8CXOVgGJDHEHEmtr+ohgz+OTnCFlT4bntbzFh5ub4yVEQHiH4Qx66CsmvLWR6GG3QHAo8+fP58ILL+RP1w0gZ9X/SIwoIdwZQI46u2VKDc/rWDLz3b+vPgy7Mszg8H8L4eMNvt9nebwH22oarog0Vgog4hdJ0bD8dvj4irJVDDt7F0xYsLuL5aAzgESGeh7f0tlNs+OE+zWdvDbAA+jXwgw91vky8qFr9x4kXvsuKU/spMX5DxEWGc3h7Ws49q9r+MeNPVn02auUZB+hxFbF2Jle9tzptgqIfb0RgCm/wKYqLKdeoAqIiJwiFEDEbyJCyq98WOz7woQGmwNNwd3N4R1eUrwCSEQItI8ve97+yeatPYDkO7/cQxJaEX7hiyQ9vpu40VMIimrC4d1b+OTF+9j/ZApH3rmY3NWfYRTlu65jl2GrgFgBpGMCnN3ODBSTvjNnt1SGxoCIyKlCAUTqFXsFJDTInKJr5x1AWjrX6rCCQWQItE9wP9+5KdzY1/wB2+qqBe5ZM78bDg8Ph+DoRBLGPkXKk7t58JlX6NhzEJQWk7fhG45Ou4p9T7bk7Wcnk5qa6tEG+xgQawn4xCh46QKzvduOm90ylWF1wVhdUUWlvsedVFVBMTz4A3xZduKPiEhAKIBIvWIfhGrvgrFEllMBOWAbpNouwf38oJbw7DnusSLW+YptK57GhsO4Lu7XBEXEcs/ke3npi+W0fHQDcec9SnBCa4y8dFZ+Ze6afP755/PVV19RXFzsEUAsTSPNEGItZpZWztLv762CSz8x1zIBdxdME9v7zquFKsinG+HzVLh/Vs3PJSJSGyrojRfxP+8xIE29KiDh5VRALJEh5hLqDszZM/bZN2AGlPBg84v+oC20eO9H0zzKPFdock8Sxj9H/IV/In/rzxQtmkrm2m/48ccf+fHHHwkJCSEqsTUFMe0IadqOiG4XEDXoOppGmn1NSdGw/UT5AeSDtbAj3dwsb3Qnd7UjOsx8/4Ul5jiQ+Ajfr6+s4/knP0ZExJ9UAZF6xV4BCQ3yrASAjzEg3gEk1DzGejzWK4CA+8vcmlkTGWKONwm1/a8hJszz2o6gYCK7nU/cTV/yzeLtxJ33CMHRiRQXF5N5eBcF2+eSs+zfHPvP9Rz/5A7iQszpK9Ziar4CiGG4KzfWOBKrCyY82F3tqY2BqCEnGXsjIuJvCiBSr9in4Yb66IKJ8woU8eGe3TJWQGnnHIjqXQEB9zkznV0n1swa+7UdDmgWhU+HQtqTMP55Up49zNKNexn59K8k3vAhsWc/CI4gchb/k389eD5Hjx51df1YAeTFRXDVp+ZCZRkF7gXL1hw2u0mscSnhIe7F26o7Fdcw4Ked5hoqIcEnP15ExJ8UQJymTjX79ocMGRLoppzSvMeA2KsQoUHQyqurxOFwT8UFdxi5tLs5PuT0NmWvkRDued9aW8S7WpLoFUCsIsLaNOf9oGDSw1sT0uEMogddR58b/0bS7d/giIhjy8p5DBkyhKxtCynNTedwtjmX99WlsPQAfLsNDtoWT/vPOnh4Nny3zbwfHgxRth2Eq2PGVnOJ+FEfeFZASqu4OFpjcTALUo8EuhUiYlEAcZo0aRIbN25k2bJlgW7KKc17DIg9gLRPgBAf/8Xax4FYFZBresGiW829Y7x5V1UinJWGWweYt6e3drbFOQ7D0tm5vsi6NPdjG4+4B5D2bQ6RPceR/MAiUtp2ZNeuXbx46xns+0MTpl4cTkpKCodfPZvsJe9zIiPH1f1iZ21oFx7sroBUdxDqzzvN28xCz79bdZeJb8gMA057D8b8t/zxOCLiXwogUq9Eh8LFXeGCjmb3SoJtEGqnJr5fk2KvgIT6PsbOe0CnVTW5vi98cCm8eZF53+GAZrbr921h3m477n5s4xF3V471fGhyTz7+fimXXnopUTFmOiotLuLgwYMUbJ/L8Y9u4d5RKTz36D0U7l2JYVuv3doMLzwEopzvpTbGgNj33amNWTUNza509+/2ZftFJHA0C0bqFYcDXh3rvt/UFhbKCyD2Coj3NF1fylRAnK8JcsCIdp7PNY1yDxTt09ycymq3+rB76myf5u7HO7ZKZPr06Ww5BqPezyeq6ChTBqVxz6uzyV78DnlHt/PT/94A3iA0uRdRg68netAEQpqYfUb2Csi/15qrqd4xqGzbK8u+S29uMfhYrR4wF0wz8F1pasiWHnD/fqp2QYnUNwogUq/ZFyJLjvF9TIqPLpiKxHuNAakotNgHvXZvVvZ5ayZNkAN6N4dgh/m7NX6kRTQ4QiPIC21NTPvWxI0aSOy5v+OMkl9YNeNtNi/4kqJDG8iY8RgZMx4jvMMZhLUbxpaD/Unu3A+jpAfLDoSy7IBZEZlcziZ+J2MPIOVVQKYugzdXQOtY+Pa6k69a25As2+/+/VTsghKpjxRApF6zh4NWsb6PaVnFLpgyi5tV8JqISlwfoEOCed5/jDEDiPW6uHD3uiPWAEhHUBDRnc9lYMdzyRmdTu7az8lZ/h8Ktv1Cwc4FFOxcwIxfzGNDQsNIaNubwk4XMj/ociYN6YejGsnA/qXr6wv4cLa5eR7AxgKz28fXDKKGapmtAqIAIlI/KIBIveZwwJ2DYMuxst0jFo8KSCWmm5bXBeOLfeGz8qblAgx07jUzvqvn4w6HOeYkLQe22faROZprjh0Jikog5rRbiTntVopP7CF/82wK96+hWeZqju9cQ2ZmJke3r4TtK/nfD8+y/OWOXHHFFZw/4be8tL4lfzwLzmx78vecbluIzNf+Mtu99rjJKaz9ALInAz5aDzf1NytD/nTQNuBXAUSkfmhkPb3SGP3hTJh2ibkuiC/JVa2AeE/DrSiA2K4ZGeJ5375uyICW5Z/DOs4+ePVIDhzwGgwZ0qQtMafdStMrXuHeN+aRnp7Ojh07ePmtfxPZ51IcoRHs2LGDF154gbGn92LZ9x9y3RflD2gosnW72ANIno8v4N1ee9VkVXPtkYq8vRJeXw6fbKj9c1fEMDz30ylQABGpFxRApMGLC3f/a72qg1DDg80uk/LYw4nD4TkmZUCy7999tQ88v+T3ZfkOApawYHA4HHTo0IF7b7+BdndNp9WfjvLK+58yaNAgSnJPcOw/13P03cs4dOiQz3Nk20KERwDxUQGxzxIBswJS23Y7r3Eir/bPXZFi58BaiyogIvWDAog0CtY4kIgqTsM92aDVi7uZt9bKqvZ1SU5r5f69a3nTSnAPerUPBLXY97ppH+/+3d71E+SALk0hKDyazmdeyaJFi4gf9ywEh5K3/it69erF7373O77//ntyctyLXOSUF0B8fAF7B5C6qIBY01/r4twVKSip+L6IBIYCiDQKQ1LML+quTU9+rD2AnKzL5ow28M1vzB/wDCB9W8B742H61RVPW40LL/85e/dRjyR3NSbcq7vJel9bjkFoaCjxFzxO8kPLCW3Vn+PHj/Piiy8yduxYmjRpwsiRI/nrX//K4d2bXa8/cZIKiHcXTG2sPWJnGLAv03luPweQQq/AoQqISP2gQajSKPz5XHh4eNnl032JDTO/6EuNynXZWAuMgWcXTGxY5QaAegcQa1YMmJWbjc7ZMUlR5mya7SfK7vrbMwlIhQ22pcTDUvqS/OBS/i/lc2bPns2PP/7Inj17mDdvHvPmzQMeJaR5N6L6XMq+IZdiNB+KIyioTAXEMNwVkDZxsDfTs/vGm2FUfYru0Vz3e67o3HVBAUSkflIFRBoF+9oblTnW6hapzLohdvYKSEwFlQ077wByQSf37y1j4NEzzO6XyUPh/I7mnjc9vdYc6eVc5GzdYc/HHcGh/OY3v+Hdd99l165dbN26lalTpzJ69GgcwaEUp20m86e/svn54Rx4ug3HP5vM6kU/U1TkLnGk5ZjdMsEO6OG8rhUS/vgz3Pq1uUAZwO9/hHP+DVnO1V8/T4V7vzv5l7p99dFsP6/EqgAiUj8pgMgpyRqIWtUAYh/AGlOJ8SbgufBZXBiMsFVNWsbA3YNh7k3m1NRHz4A1d0KfFp7nsALJgWw4luv7Og6Hg86dO3PPPffw/fff0/mvR0m88WOiBvwGR3gsJRkHyP51Kq9PPo/ExEQuuugiXnrpJX5YuBqjtJRWce73l11oVoj+sw5+3AkrneNcP9kAO9PNnXtP5MGDP8DXW+D7bRX/DazuF6heF0xxKbywEH7dU/XXeo/5UAARqR/UBSOnJOuLtjJdMHb24yu7Toa9ApIUDcNsg1ftXTpgdm1E+zhvbLjZPbMz3bMbpjylBhSExBE98BqiB16DUVxA/pafyF37BUbqV2RlHGXmzJnMnDkTgKDoRIo6DSAzuSXpJSnM2tGStkd7YRSPwBESxhGvDdz2ZJrhxHLUFoq+2QLvrYbXxrh3L95nr4BUI4As3Q+vLYNvt8KciVV7rfe0WwUQkfpBAUROSdXtggmxDQ6NqmQFxCOAREFb22yX5CosyNW7uRlA1qed9FA2H/W87wgJJ7LnOCJ7juPqHm9zXdIaZs76mec++Im8bfMozTnGobU/cmitefw3P8E3r4AjMoHIXuP5vvRyTr9tNGAmpvVpsNW2rok9YPxnLaw8CN9tg9sGOp+3VUCqE0CsHWx3ppsBoiqfm7pgROonBRA5JbkqIJUMEZYwW6dlZQdixntVQBwO+N+VsPoQnNuh8tfu0cysLmw65vl4qeG5lsnPO+Hmr8s/T35JEAMGDKA0eQDvRD6EUVJE4Z7lXJi4leNpB/lp7UGSjQOc2DyPo2mHyV3+Aa8u/4B3H4/C6DyGqD6XsrjnhQRHu6cc2QOGteroDtvqqvu9AkhVB7Jas3gMzAXdejev8HAPCiAi9ZMCiJyS4qvZBdOxnB15K+JdAQGzG8beFVMZ1lojG726YPKK4Egu3DUT7h0K762q+DzWF7DVNeEIDiW8w3CuGz+cg9mwcg6c3QnuGVjC6OcXkrf2C4yNX5B9ZA+s/YK8tV9AUDDhnUZywbhLWBF/CXsTzXXyDcO9QZ99eXd7haTEMMdlVKWKYV/HZGsNA4jWARGpHxRA5JTU3BkE4iMqPs7byHbw2JllZ6lUxF4BaV6DPVC6OQOIfUl3MNfseHERpB6Fe749+XmsabiZBZ6Pt0twLxKWXQh5pcFEdDqLiE5n0fP2l7gleRW3/d+X5K37kqKD6yjY+jPf/ONn4H6Ote7Hk1su4ZzRF5NfPBCHw+EKIIbhWQEBcxZNVQKIfR2TrcfKP84XDUIVqZ8UQOSUdG1vc2bFVT2r9jqHA+4aVLXX+KqAVEfrOLNi472OR16Re5psZVib0XkHkDZx7vVAcgoh1zZWY1+Wg7ZnDyRh3EASxj1DStF2Rhd9xU/ffcWvv/5Kwb41PPvsGp599hmC41sR2Ws8eb0v5sjV5xAaHuFa2MxaA2XpAfj3Gvjd6TA45eRtti/fvuV4+cf5oi4YkfpJ03DllJQYBQ+c5p6lUZdivcaAVJe1JLu3nKKqDez0VQG5f6i5+Jk1syer0HO9jswC91oefZvDooc78dRjDzJ/3lz6vXiYptdN47wLLyciKpqSjP1kL3yTI2+Po11KM664/DKyF79HQvFh19ibj9fD4v3mbWXYKyBbalgB0WZ0IvWDKiAidSwkyFw1NavQ3fVTXd0SYa3XLJjcIs9BoENS4Ioe8OhPvs9hhRUrgNzQFx4cbv5uTQHOKSq7Xsdq51og3tOP26U040TwRH5/0UQOnMjn9+/MIW/DN+St/5q8jP38/N2XwJcc/xiiW/XC0e4sVvU9i+IWZ7E3s02l3rc9gOzJMKs+lR1AXOgMHHFhkFlYuxWQzIKKl9oXkfIpgDhNnTqVqVOnUlKiEWpS+x4aDpuPQbcqjB3xpYuPTe9yitzVibsHwU39zUXNmkeZ//q/22tcyIEsKCoxv4zB/GK2xDp/zy4sux/MsgPOY7y+cK21TE7kw7GiCCJ7jiWy51iMK6dyecJqdiz+mlnffkPh3hXk7N8A+zewYeGbAHzVrD13/Tia8ePHc+655xIZ6bUwilO6rQvGALadgD6VHIhqdcHEhdduAPkiFX77A/zhTLizit1yIqIuGJdJkyaxceNGli1bFuimSCN0c394/jzP6bLV0c1HANmbYQYNB2YlIznGHKtyXkdon1D2+OJSc78XqwJi/xd8tLOqkFNYtlsn9YjnMRZrefoT+e4ZME0izJVZC5IGMOjaKSQ/tJw/fJ3Gmb/7gtiRDxDWZhA4gig4uou33nqLiy66iMTERMaPH8/bb7/N/v37Pa5hVUBaOLuwqjIQtcAWQADya+nfGL/9wbz9y6+1cz6RU40qICINSFcfAcQalNkiBsK8dtEtb7XWHSd8B5C4cPdGfdY6Hikx5hLwRjnntAJIeh4cdi4YNrw1fLvNPIcVHvp0SCKNy9jT6jIASvMzKdg+n9ElM5k7ewZ79+5lxowZzJgxA4ABAwZw0UUXMXrseLILBuEICmJYK3Pp9/LGgRgGPDXX3NfmyZHmY4XeAaQGFZBjufDNVrism/vvdDJ7M83g5P3ZiJzqVAERaUBaxri7SSxWNaBVbNnjvasVnZ2DWHekuzeUsweQ8BB3lWXRPvPWe5aKdwBJsHXBWONG+iebt9tPuMeO9E/2fG1QRByRvS7k9idfZ/fu3cxfuoZnn/0Tw4cPx+FwsGrVKp599lnOPH0oB55uw4lP7yZs5/cUHd3O8g3b2b7d/MnLc/fP7EqHaWvg3dXuCo6vAGJUIjj48u4qmPKLuQx9cCWqWUv2w5nvw29nVe96Io2ZAohIA+JwlB0HYm0U1y6+7PHe+8p0d762vAoIuMPDEef+Lr2am9NnLeVVQE7kQ66zutClqfkv/qJSc9ZNVKj5mK99bvZmwq97HFy/sC+x5/+RhQsXcvjwYf71r39x5ZVXEhUdQ0nGAbIWvMlLk8Zy8E+d+fyuznTubP40b96cG2+8kVmzZrF4j7u8Yb0/K4BY67GUGmY3VHVYS8Kn5VSuO+2lRebtjK3Vu55IY6YAItLAeI8DyS82vwxv6lf22PBgz3+pW104OysIIAOSPe/Hh3t2/ZTbBZNvzk6xjrGPP+nTHIKDPBdls+zJgNWHzS6e+c7dbmObJHGo8408/uqnzFx9hKQ7viXlnDtp3boNjvAYHOExRMfEEBkZSXZ2Nh988AFjxozhtrNbcfyzyeRvncPxHDOMWNNu7e+zut0w1tTk7EJzdtPJ7Eyv3nUagpJS+OPP5nouItWhACLSwFzdE/q3gIEt3Y/d3A/6JZc91nt3XSu8bK9CAIkONfehsZTpgrFXQJxf0JGh0NW2Zkm/FuZtUx+TXPZmuhcas8advL0Spi6Diz+BHMOcWXPaXW+yd+8eRr6VRZu/ZjFjXRY5OTn88f1fGT/hHpo1a0ZuehrZv04lbeq5DO/Rkkuvu53187+hNC+DmDBzoC5UP4BYXUxZhZXrgjmcc/JjGqrpm8yuqCd+CXRLpKHSIFSRBmZgS/jqN/DqUnPX2dax5jTf8sSEusOGFUCs7hUoG0A6N3WvWwJmgOmZZDufdwXEGgOS5642RIWaq5wGOczxJtf0ch7rY+n7PRnuLp5jeeZ5lh9wP2/tA2Ndp28L85xrDkP7BAcfZJxB3JlnsG7qy/T9/Y/krv6UvPVfkZ1+lK8++ifwT3AE8UqPQWSmnE1Ix3M4mn4mSdE+Bs2chL0CEnSSf7419hVX5+0JdAukoVMAEWmgLu9uVgxu6e97bIUlyvZc0yhzOXh7APEe1BrkMCsWv+4175+sAmLvgrHGdkaFQMtYeHWs57EJ5QSQRFtlxL6JHbirItZr+7WALzfD2sPudmUWwLLDoe41SEqKKdg+l9w1n1O8dTb5advYvXEZbFwGvEDf90M579xzueSSSxg/fjytW7cu2zAfrApIdiUqIJuPun8PbYS1ZmtwMZTdkVmkMhRARBqoVnHw99EnPy7GNhMmNMjc0dcKIOHB5swXbwNa2gJIGLS1LVkfU846IEW2gZ1R5axS6qsLJqPADCGWHSfc64kArDjoeR1rAbLUo2YlxPLDdvfvjuAQIrqeR0TX8wAoPrGXi8Lm8sOPc9i7dg7Fx3Yya9YsZs2axT333MOgQYO4+OKLGT9+PP3798fh8P1tmm0PICcJFVtte9YUlZqLv4U2kqm42YWw2/aZ5ReX/5mLlKcR5nIRsbNXR0KDoEOC+36LGN+vGdDC/XtMqLlrcF/nbJi2XrNtIkM9Z8lA+Tvd2rtgokPdlQ97kNhy3L0pHsB659LzVnhJcfacHMl1V0cAZu8wb70rOgAhTdpwzsXXM+vTd+n41A5aPraJq+7/K6effjoOh4MVK1YwZcoUBg4cSNu2bbn77ruZOXOmxxRfcAeQyowBsVanteQ2oi6ZHV5Vqtwi38eJVEQBRKSRs3eZhDgrIJYxnXy/pr9tIKr1+o+vgPk3u8di2NkfC3aUv+hWgu24kKCyYQZg/m7PDeSsyorVBZPo3E+nsATW2LoBrE32RrTzfe2wEHM2zx/OgtAW3Vjd+fd8OHMBBw8e5N133+XSSy8lKiqKffv28eabb7pWZ73ooot488032bVrt2t5eu8uGF/ritj35wH3DKHa9O4q+M3nVduMsDZ4b+inACLVoQAi0shZpfGwYHNWTGtbd8ql3X2/JjEKHjwNbh3g3sE3Osy9FLo3e2UjKtS8ji/2fWeKSqGNj92IN5Wzyql1jYgQd5XD+9jYMOiVhE9WlWZiXzizjRly/rYIWrRowS233ML06dM5evQoM2fO5K677qJNmzbk5eUxc+ZM7r77bjp0aM/ev/TixFcPc3zDT5QWubcTLvKxroh3AKmLL+m3VpgLxtkH7fqD9w7DjX3ArdQNjQERaeSs1VCtdSuGpphVjR7NoGcFm+PdP6zy17APLq1ol1p7MCkqgTY+KiCWuHD37B3wrLI0i3LP0rFLifW91gi4qzIOBzx2Jlz4kbms+0PD3WuWREZGMm7cOMaNG4dhGKxfv54ZM2Ywc+ZMFi1aRNGhjRQd2kjWnL9xNDyasM7nENl9NOtHjWZAz84eY0fKdME4A8iMLeaibDXdmDCjwD3NN6Og4mNrW6FXAFEFRKpDFRCRRs7qQrFmYiRFw8Jb4INLy69UVJVHBaSS/6wpKvWcXRMf7rl0/BU9yr9Goo9uIDCXqveeVmyxj1Pp3dwc0wLl7yvjcDjo06cPjz32GL/++iurth8lceInRA+ZSFBsC0oLcsjfMIMTn9/LoN5dadWqFVdddRV///vfWbR4CQfSCzEMg+DCDIqObGP50qV8u+Yok76DCz50/g1K4JrP4PE55n3DgH+tMXfaPZlttkGuGfknP97bsVx4bSkczj75sd4UQKQ2qAIi0sjZu2As5VUJqqtJJSsg3gbaxppEhppThNc5B52e3xH+twHXuAv7NZpF+T5fSmz5AcR7XEpyDKxNcy+vfjLB0U2IHnA10QOuxjAMig6sJT/1e/I2z6J0168cPHiQzz77jM8++8z5gjAwSqHU7J+4GTPUhLYZQkSPMSwaOgZH66Es3h/M4v3w5Ah4foE5rgPggk7lbyYIngEkvRoVkA/Xm11QR3Lh6bOr9lrvLpg8dcFINSiAiDRy3hWQumAfXFqVAJJiWwvsUDZ0tg2Q7dvcHDBrBZKEcgKIA/f6I94BpHUs7HN2hXgHkObO8SxWACkpNRdCa17OOJccW5ePw+EgrFU/wlr1I27UI3x1eR5Zu5azYMECFi5cyLxfF5Jxwl1acYRF0yQhjuNpByncs5TCPUs5fdYzxCU0pbjjaCJ7jmP6ijG8u8pdEtqbAT3KGc8CntN8q1MBsSofm8upAFXEuwJSFwNspfFTABFp5FxjQOpwDYrqdMFA2S4g+2JWseHQyRlAYsM819BIsgWQLonubhTvAHJaa/jM2Z1RXgCxxlHcNRN+2AGfX1V2B2CoeKaJERrJWWedxVlnnQXAV5sM7vnvLga0CiUmPpFFhyP5+wVw4MABprw7i/zU7wnd9QMZ6cdh5UfkrvyI33zoIKztUCK6jyay+2h2Hh9Kj6Ty/5geXTDVqIBY42u8F36rjDIBRBUQqQaNARFp5PxRAfGeBVORy7p73k4abN5e3NUcHBoRAo+cbj7WybmfjPfU30RbABlk2xPHewzI0Fbu370XXPOugPzgXEfE6gLxVlEA8Z4Fsj/LQUhiB7q0b01cjNn43CIIb5JCzLCbaXbTJyzcdIS/fDifuFGPEZrSDwyDwt1LyJz1DIf/cQZXDUniyiuv5K233mL79u1lrmmvgGRWI4BYoSUtp+qv1xgQqQ2qgIg0clYA8bXiaW2xB5DyFiGz/OVcc/0Ra72O355mrrw6rJUZHjZPch/bxRlAkrzGfDTzCiAfrTd/954FM9y2wrr3YmmuAJLr+XiJsz9nTwb8uAOu7W12K+VU8CVrdUGk55vjKlY61ydpFeeejptb7NmNk1EUQuveZ5Jw0ZkkXPQXitP349g2iyb7Z7FxyWxys07w+eef8/nnnwPQoUMHRo0axXnnncdpZ53Lvkx3/0x6Nbpg7K/ZfqLsJoQVKTMGRAFEqkEBRKSRO601XNTFHNRZV+xjQE5WAYkKhTGd3fdDg8tv23kdYNIQOMdrcTErgIQEmZvnWZJjzKD16ZXm/iRt482AcjCr7NgOVxeM1yyQUmcAufYLMzzsyzIHiFZUAbG6IF5ZCv9e6368VSwcdwacvCLPqcPH8yDLVnkISWjFdTfdQr8Wt/D72SX0KlzG6YWzmT17NosWLWLnzp288847vPPOOwCEpvQlvPPZhLcdwv78QZSUdCU4uPL9bPZxI9uPVzGAeFV81AUj1aEAItLIRYTA1HF1e42qdMFURVgw/P70so93SzSrIv2TzcGqp7U2B5xa1Rd718tnV5nTXb0rQNaiasfyzAGoFut3q3LxzRYzgORUogvGvqcNmG2yxmrkFnmGmBN5Zdcyubw7FBvgCAomL/k0nph4Gk888QRZWVnMnTuXn376iZ9//pm1a9dSdMD8yQYWAgl/imHAgAEMGTLENR4lMTGx3Dbbx41UdRyIumCkNiiAiEiNVXcabnXFhZtrmYQGmQNZP7mi/GODHL67nxIjzedKDThq2/KlxGtZdWt8RHYFX7JWAPFeKbZ1nDuQ5RR5hphjeZ5jL4akmINfDzhn7ezLNMNQcBDExsZy0UUXcdFFFwHw5Iw0Xv90Ds2OLWTXxhUU7l9FdnY28+fPZ/78+bz00ksA9OnThxEjRrgCSUqKObq21KjdAKIKiFSHAoiI1FhcuHs6bFVmwdREefvNVFZwkNmVk5YDabZumBKvZdWtcLHKtivvCa8xF9YYCO+xES1j3QHEuwvmRL77/h/Pglv7m2EqOcb8WxaVmt00ST6mBR+iOdEDr+GuYdfw9yVglBTz1XmbWLt6BYsWLWLevHmkpqaybt061q1bx9SpUwHo2LEjZ555JkOGj6AgbSQhzTrhcDg8ZtRUhhVAQoKguFRjQKR6FEBEpMaCg8wdc9Pz/VMBqS0tos0AYt9avsQoG0JWHITlB82Ky3V9YOoyz+etCoD3bJKIEPffw7sLxj4GJD7c/BuCeZvgDDnlBZCtzmnHA5wzgBzBIbTu3JsB/XozceJEANLS0pg3bx7z5s1j/vz5rFmzhh07drBjxw7+/e9/m9eKa0lYhzM4Ed2UuxeHEBYaQlhYGF27dmXgwIH07t2b8PCyK7tZASQh3Kwe1aQLJrfIHIfToQn8c6U5hubjKzzXiLGk58NPO2FUx8ovpldqeE7vPpll+82KWd8WJz9WakYBRERqRRNnAKnNMSB1LSXWXGfE3gVRUlq2wjH5W/N2fFdzbRJvVpXE12wUqyLkawyI9cUd67XiadNIsw3H8iijqAT2OMendG3q3jPnWJ4ZDFo5N/hLSmrO+RddyZVXXglARkaGqzoy6+f5rFy+lJLMg+StMVdufXNh2WuFhITQo1dv8poPYdRZp3HflcPp1q0bBSVmWoqPMANITbpgJn9nhoqfboBn55uP/XUB/GNM2WPfWA5vrjCD3dyJZrWoIrvS4dJPYGI/c7bVyWQWwITpZgBZc2fVgotUnQKIiNSKJpGwMx0iG9D/q7R0foHZA0husVl5sDuQbX7ZPTgcNh4pex7rC9g+s+RB5xeeqwum2DOAHMszuy+g7PLxiZFmm7zbAWb4KC41/87JMWYlILMA7pwBuzJgxrXQpzm8tNiclfPxFeZ05Pj4eMaMGcOYMWMYtweu/SSP5ulLydu9nAPHc7moUzHt4orJzc1lw4YNrFixguPHj7NuzWpgNdtmv8ObT5rniWk3kIyEPiT26EtBVB+yEnsB5SwhexJW94/9Mygv0FjH5hebU69PFiqW7DeD3HfbKhdA9mWa3WgFJeY1GlKYboga0P9V1K2pU6cydepUSkpKTn6wiJRxfR8IccAZbQLdksqzAsgO25dfdkHZL/7WcfDR5dAmruxMF3APLrUGdn5xtXuBNGsJ+b0ZngFkZ7p71o6vCgj4roBYbe3QxBwzEh8BezPN8AGwPs0MIKuca5HM220GkB0n4D/r4M5BZjuDwiJp328krc8ayZeb4VgzePtq95euYRjs3buXW95YztKlS2DfYor3LiMjI4OMtXOAOaya53y/Dgc9/tyNYcOGuX769OlDaOjJv8Gtv4m9+6rU8H2sfeCsd5XKl6POKdD7Ms2N/k62+eJB21ig3CIFkLqmAOI0adIkJk2aRGZmJvHxFewRLiI+XdGj7A629V1L5zgD+7++swvdX/xxYXBNb7ilv3tMgndYAPcYEqsLxr5w2uAUczn8A7Yvt5gw8zquLhivCoi1zokVhHacMI/v28LdVqsryHssxJFcz7akHjVvr/vC/ILdlwnntHe+NgK6NwM2w8aj8OJCeHKk+ZzD4SCldVsOtW1Lk+TLiQqFtbcXsW7dOu59fw3r1q2jSeY69m1bR2nWYTZt2sSmTZv417/+BUBERIRrWrD106VLF4KCPJfktQKIfU0U7zE4lqO2ReNyK5gW7X18TpH59/BeUdfbIdtnpJk9dU8BREROWSnOCoh9EGV2kfuLf3gbePwsz9f42qF2+wlzcS7rS8seCiJCzEGTX212P3b3IHhhkft+eRWQo7nmImoXf2ye+6cb3BWQjgnmrX2TPoAjzqXlrQCyyRlArH/dL9rr3oU4IcIcVPvuKjO4WBv3WdYcds/UyS2CUkcoAwcOpO3OgezrbAaz91ZDcyONp7suZ/HixSxZsoSlS5eSnp7OokWLWLTI/UZjY2MZOHAggwcPZtCgQfTuO5D8oi44goI8KiDeU6Et9gBS0bRoX8fvyzx5ALFXQPw9s6ekFBbtg15JJ29nY6EAIiKnrJY+ZlrkF7v3h2nq44vAHkBSYszKRloO7Hd+eTsoW9EY39UdQBzADf1g6vLyKyDWdY/nwVNz3SHg81TYaQWQk1RArPEoB7PNAa+WqDB3OIkPN38ePwvun1V2tddf93jeTy+AFiG2WTDO8JMf0ZwxY8cxbpy54l1paSnbtm1j2bJlrp9Vq1a5FlSbO3eu65yO8BjCWg3gkwEDyQ4fQFir/hSn9AQ8+z/yiz2nMVdm5s0RWwDZmwl9TjKz5ZAtgPl7cbUvN8ODP5i/v38xnNvBv9cPBAUQETlltYh2r19iZ3Wp+Aog9mpF0yjzX+uHc2Clc52QuPCysydGtDW7czILzdfHh8Nl3eDD9eYeNd775yTaxoAsP+B+/ItU8xzg3qivTADJMQepZtq+rH/c6f49xOEeS2G91npPVgCxxkvM9wogf5oH1/d1r3fSuanzfRWYYcXa3ycoKIiuXbvStWtXJkyYAEBxcTGpqamsWLGC5cuXs2LFClavWUN+XjYFO+azeMd813U+CQlj03O96NGjBz169KB79+40bdMDo7gzjpBwj7ZWxD6Gxru648vBAHbB2Lt/PtmgACIi0qiFBpt7whzO8Xzc6uZI9BFAIkIg2GEGj7BgcyzG4RxzrRAwx1V4Cw+BCzrBZ6nuCsrEfvC/je5Khp0VfPZkuLsjQoPcX6JxYdCjme/rpeWWXY/k682ez7sqIM7XxjiDSHYhpB6B33xhdq9YA1mjnZvxfb0FNh0zQxuYAebyHjBtjTnA1QogvoSEhNCnTx/69OnDTTfdBMCag8WM+cdmivatpGXWSrZuWEXh/tWU5mewatUqVq3ysTVxUAiOkDAOhITR6rdRtG/fnm7dutGtWze6du1K37596dixIw6Ho0wXzMl4D0KtKsMw/06+uulOxr66bEZB+cc1JgogInJKaxlTNoCsSzNveyWVPd7hML9gMgogLMisRCzc5w4gCeUskHVZdzOAWOt0dGtmTpn1taCWFXysL8TwYLikmxlYAE5vY65CCr7HgHjPEJlnq2QUlrgHsloBxKqAZBbAnF1mQHlpsflY23izPVYY2XnC3XUVFgwT+pgBZPYOc7yKr26t8uSXhhDWshdhLXvRo9UNZO43Z9/0DNnF3W3WkpqayqZNm0hNTWX9xlRys7OgtBijsJjiwlwO5KZz4MABFi70XMQkLi6Ofv37s50BhLYeSFjrAexp24OKvvIMo+ZjQJ78Bf67Hr691vx8q8K+wZ93gGysFEBE5JTWMhZWHy77+Mh25iZ3vsRaASTYPRtls3N1Ul8VEIAz25p9+/aKR/dyvqSaRnnejw2DK3u6A4i90uC9hkheMRw4yb/2rfU0rPATY+uC2ZnueWzvJPdCa2AuEb/fef6wYOiaCKe1gsX7zbU5Hhxe8bXtsm1ftFa1wuFwENm8A5dc0oFLLrnE9fxH6wx+981xWoTncyijkPiQAv49Lpvt27ezefNmNm/eTGpqKhs2bCAzM5P58+YB81yv/yA0nI39+9KnTx969OhBz5496dmzJ23btiUoKIisQs+qR3UqICsOmt1f8/dUPYDYKyAKICIipwBrJoxdsKPs7Bc76ws7LBi6NPV8zte4EUtl+/WbeoWYuHBzs7oezcxumXPbu5/zVUHZ6gwYsWFld9wFd7dOglcFJK8YtnltTNcqDo7lej5mvT7cuR/PDX2dAWSDOZ4mLhxuH1jROzTZ22YfMFrqYxrusTwHwdGJdGkNR/dBcTAMHgyDBw/2OG7HsSLueC+VZpmr+HbeKgr3W906ma4BsXYRERF06dKFlA7dSM/rSkizzoQ07cDerh0o6d6a4ODKbzpkdZ1YYbQqCtQFIyJyavHVZXBtb/Nf9uWxAkhocNml2XtU8V++voQGu5dYB/fA1k+uhPwiaGELTb4qLlYA6d3cnNppGdvZXBXU9VpneIm2jVlI9VrptVWs70AAEOb8Brmgk9nGtBxz9VUwQ4n34Fpv9oGk9n/1e++2C+4di9vFm++poMS9kuyyAzAg2bzes7+GsjWsL1ub9aXJ5RNpHw87T5RSfGwHf+6xij3bNrJxo/mzZcsW8vPzXZv22T08FR4NCaFt27Z07tyZ7t2707NnT9eg2KSkJBxeK5tlOru+ahpAsgqqvodNQ6QAIiKnNPumZ2e2gZ5JcO/Qil9jr4Akx7gHaYLvcSPVkRjpGUDAPW3WznsMCMAW5xdgM6+unHZeayxa5woLNqsZBSVlZ3+0ii2/S8DakTgsGEZ1gC82uZ/LKKhaALHzNQPFqsK0T3A/llsEH6yF/1toTnV+bWzZ2S6t4iCnKIgjQZ0ZPKozN09wP1dcXMzu3bvZvHkzH8/dwvRfN1N8bAfFx3dinNhFcXGRawO/H374weO8cXFxdO7cmS5dutC5c2c6de7Ckc1dCEnqwuagRA4cTOPA/n3s27ePjIwMevToQZ8+fYiM9F0is4cuA7M6VNkN9xoqBRAROaXZNzQ7ow3cM+Tkr7HW7QgLMgelJse4B3bWVgBpGukej+G9TohdRV0w8eFwUz9zkOgzZ/t4rS28xIZBgY+l31vFuQONtzBb78SYzl4BJN+8fqlR/pLmmeUEEF/jL6wumpYx5oygolJzCfx3VpqPf7PFDCDeq6g2izLPdyS37FogISEhdOrUiU6dOrGl6Tjmprifu61fCTd1OsDOnTvZsmULqamprp/du3eTmZnJypUrWblyZdnGOoJodV/ZslFQUBDdu3enX79+JCcnk5iYSLNmzUhMTGT7pgQKTsQTFBFPUGQCRzLjiU+qfAIxDLNfzLsqk1MIxUb9DDMKICJySrOPAYms5N4f9goIeJbPE6PKHl8d9inA3gNNfbXFzhpDkBABk4eYM2gGJJu7zlqiQj0DREyYu5vDrnVs+ZWKcNvrR7aDns3MJd2tNpz5vnm77i7f1ZByKyA+Aog1SLVZlNn2jAKz6hQb7jnrp8hHADEMcxZPRWuBWDNgrHCTXxpMmzZtaNOmDSNGjPBsX14eO3fuZOvWrWzbto2tW7eyLnUrS9ZupSR9LxilOBwOWrZsSevWrYmOjmb9+vUcOXLE1f1zMl2eMANSTEwM0dHRrtuoqCgiIyOJjIwkJyeHI0eOcOTIEY4ePUpQUBBNmzalSdNEmjZtSkJ8HD/vDYeQcK7qE0HnTh246aabaN26nNHVfqYAIiKntObR7nU9Krv5mH0MCJhLm+/LNM9TW5pWMoBUNE4gIcIMVQOdG+PZu5u8/0UcU8414sLN6sYbKzy7msAzgESEwHcT4KKPzGnMaTnuqsWudHPGz9bj5jTh050bFpYXQHJ9dMFYASQpyj0NOqfQ829TapStgCRFudtZ0VogVgBpl2DOEvLVDbT2sPm+RnWMdM2isaw7DBd9DKWFeZTmHud35zfngdPd/0EZhsGBAwdYvXo1GzZs4OjRoxw7dsz1s35PBlmZ6ZTmZ2Dkmw0tLi4mPT2d9PT08hvu/T4OHuTgwYNlHv/XCvP2qaee4uKLL2bSpEmce+65ZSom/qQAIiKntOAgc0XUA9nmFveVMaoD/LAdznPOavnTOeYX4Q19a69dHhWQSi5sFRLkHpgJ0MRrfEirCgKIr032wOxi6p8MP0yA5FgY8o674hPmY4KIdd4029oq1viGUR+Ytz/faA7eLS+AFJdCUYk74BWVuKscVgUEzDAUbQuNh7M9AxKYf0crpFQUQKyVSDsmmAHEVzfQXTPNJffn32Suj/LVZnNA7LNnu6tOQWGRBIW1YpvXrskOh4NWrVrRqlUrLrzwQkpKzf/2LFd+ag6mBTBKS/jbyCyGN88mJyeHnJwcsrOzyc3Ndf3k5OQQHR1NUlKS66e0tJSt+44z4cNjlOQc49Eh2fxlbgFGUT43985n5a8/MHfuXKZPn8706dPp1q0bd999NxMnTiQhIaH8P04dUQARkVNel0QzgFR2Ea3TWsO8m9z34yPgz+fWbpvsFZCKxoDYnd/Rc5ZLuwTP5+PC3Tvxeg9etQeQCzrCDzvMbhuLta5FuwRzTEiww/ML1GKNK7EvLZ5d6FmZSD1iBpCsCqab5hZDfLC5MNpTv5iPBTnMdlsVqJwiz6m820+4V3m1NItyV4n2V6IC0sE5q8lXN5BV0VmfZgaQ+7437w9JcXcxWUv7lzcTJqPAXNL+q83wyhizugSeg1AdQcGUhifQunVC+Q0uR2lcOyK6mb+fewW86jzv7ddBjz/9gQ0bNvDGG2/w73//m82bN/PAAw/QokULfvOb31T5WjXl4z8fEZFTywujYNolMLhloFviZl+MrKIuGIBZE+Dps+EezyUx6JDged/hcHfDeE/ftY8luW8ofHIF/OvSsteyzumr+gHuCog9gKTn+x6nUdF+LlYAuOkr2OWsJiRGmqHHVQEpdG+6B+7VaO2Sotzv+VBO2eet81gzfaxdhr27YIpL3SFhyzHPQHXEtvx9D+cg5B0nylZRth6H8z8wF5QrKPGcIm2du5kzeFZ3LRB7Bci+tkq+8/y9evXitddeY//+/bzxxhucd955XH755dW7WA0pgIjIKa9FDJzT3vyCri8qOwgVzPEVN/XzXB8kOtT3XjbWoFvvc9oDSIcmZpXH18wJaxrsyQKIfXn7jALPxcxO5MGy/bDBueZIe6/pweC7AmFNK7ZXQOxf1Ev3+36NNdMpPd/3eQ9ku8/bPNr83Ts82O9vPobHPjMO3EGoe6K7K6zH6+a4Ecu01ebfxRorZG+7tRR7kvP61V0N1f7+7N1g+V6BKjY2lrvuuosff/yRsLBqbF5TCxRARETqocoOQrWzB474cN+ByhoHUl4XjDXIszxWBSS8nA58q7Jy2FYBySjwnGFzJBf+OMcc+HtJNxjmY1KGr4GoVgCxKiAZ+Z5VlF/3ln1NYpT53qyxIvbKjMXqmmkV654JlVdsTu39PNV53yuA2PeNOZHnDgzxEZ5dV6sP2Y6zQoqzO8veXeSqgDjfY3UDSE4lA0h9oAAiIlIPeYeJygix/T96dDkh4to+ZrXniu6ej1uhw77Qly/WXjbR5cwYcnXB2L78MvM9KyBL95tf4iFB5gBOXwHLqjjYn3MudeG6tj0EXNDRd1vCgt1rtXi/xrLfOT23VSxEOYNVZgE8+AM89IMZMOwVkF3p5o/laK67mhEfDg/Z9sOxj1Gxxry0dm5I6FEBcQaQJGcA8R7LUlm5DSiAaBCqiEg9VJ0KiF15VYw+zc3xLt6sf5UPTSn7nN2QFLhrkOe/8u2sCoj9izCjAI7ZKiDLnWM1hrUyj/f1/vKKzMBh3yXW6tax/jbLnbNGYsPgnfGw6ag5uHNPBszY6rkSbEvnYnEVVkDi3BUQ+5f3vkzPAbclhme15Uiue6BwfDgMbw239od3V3tWaKww4gogtpBhBRBrb6HF+8zZPyFBsGCv+fl4r2zri/3vfrieBxBVQERE6qGIEPNL7LLu5jThyurs/AK7okfVrnduB1h8Czx8esXHBTngsTPdsze8+arWpOd7BhDLKOc0Zp8BpNj80rQv8mZt5mdd21r0zAo93ZvBI2eYwQbKBhDwXQGxFihrHet7LZh9WWXHhPyyy/370Tx3mLDaYgUSe1eKFUDaOAPIsTxzgbTCEncXzJjO5kDUwznmTKRvt8GE6XDF/8q2y5eG1AWjCoiISD315Miqv+a/l8OKAzC6U9VfW9lpyBXxFUC8B6FazqsggHjPnHnmbLjSGap6JZk/1iBW72ue1dbc92Z8V/djyc73diAL3l1l7vkz3Dn2xKMC4uNb8UAWxHgFE/sMk6O57oGl1nuxKlDZPrpgrACSng+XfmIGTavSEx0G1/SGqcvMfW6s8+zyWlekPJUdhFofKICIiDQiLaJhXJfAXd/X7rwZ+WUrC52butcp8bXQ2s4T5m6+YI6LmNjP8/mre8GUX5zX9AogHZp4rtMC7grIrO3u8GAtiGYfA+JrzZX9We5uE1+O5UJEsGdbrOCQVWiOeXlnpbtLxPtc7652/x4RDBN6wxvLzWm6SZXodrGzV0DsVaeCehhA1AUjIiK1prIVEKv7BTwrINaCXjvS3QMxfe34e2k391RgX897swah2isXt3wFS/Z7BoOw4LIDbPdnuisLvva0KSp1T+W13r/1nrIL4a0VZneKpXl0+dOYw4LNSsz5Hcu2tzLsXUWlhvv3+lgBUQAREZFaExturoth5z0IFeACWxeRPYD0cA6Gta9q6itgJES4u5ma+ljvxJtVAbHblQFXf2Z+UYcHu8eMeF/vQJZ7YbLett2O28a7py9bYzisCpC9AuK9KmpMWPkzm6xg4msMj3211PL4WkIeFEBERKSRC3KU7cZIz3dPW315NLw6BgbZVp21B5CezgCyO9292Jf3njaW359uriNyYyX24PEOIJd3d48pCQmCe4e6l2z3FUCsL/aUWPdqpQ+dVraLxAoWVjA5nA17bUvAhwebIcPX3jshQe7ZNvagY8moxNTccgNIJcKLv2kMiIiI1Kr48LILaRmYYxsu6172ePuXcbsEs5sjv9jcVRfK72JpG2/up1IZCRHml799uus9Q8wVZOMjzHNZvAPP0Tw47qzgRIbCtEthbwaM7QwfrjO7iwBCg9xdNFYFxLvyY4WtAh+BwN4tkxLr3rfHklHgXim1PKqAiIjIKct7IGp8uFn1+Mt5vo+PDnNXHyJD3KutrnSuF1KZMR4n43B4VkGsJdf7tPAMHwBNfHTp7Djhbl+f5uZAX4fDc6qvffXZ8nYXjrV1zXizBxCHw11psVRmfxgFEBEROWXZxzf8bjgsvx0u7lb+8UEO9xdzeIh7tdXtzi/98rpgqirZNs24eQWVBF+BZ5uzLd6zeRLtAcT2uvJ2MLYe97UTcLjXwFTvdlSmCyZHAURERE5V9gASF17+jA8764s5LNgdQCwVhYWqSLFVQCqa3uor8Gw7bt5GegUQ+3nsY1miQssOxgV3pcfXSrXefyfvPXKO5cFffnUvgmYY5nTd2c4ZNvsyYXc564X42oQv0BRARESkVtkrAb6mrfpifXmH+wgg1jLxNeWrC8YXewCxpuRaU1qjvN6PdxeMxV7VsbPW43jzQnPa79nt3M95B5AHhsENfd37Ak1bY07pnfiVeX/ZAXh+Adz2jTlG5ex/uceqeKuPg1AVQEREpFbZv4i9KwblGdnWDCG9m0OnBPfjwQ738vI1Za0FEhLke5yHJcH2XNdEz+e8u2CalVMBAd9VDqsr5My2sOBmuN42g8d7h+GoUPjTOe4py6lHPJ8/kOX+fe5ucz2S8tgXIjuYBRuPlH+svyiAiIhIrfIIIJWsgDx6Jqy+wxwQaq+ANI+ufBXlZKyl5pOi3F0hvtgrIN7Vl4gKAoj34NsY59+hjW3l0zyvsRitbeNSvMeAuM7rPE+JbWExw/AccPrDdq92eQUs+xiQm76Csf+F1Yd8X89fFECcpk6dSs+ePRkyZEigmyIi0qBVpwsG3Gtg2AdwlvelXB0Dk81umLHlbKRnqSiAeHfBJJXTBQPuLhj7OYq9qhStbOGkvPfqa1BsTpHnbrc/7/J83ntfHyuAlBqwybkw2j9X+b6evyiAOE2aNImNGzeybNmyQDdFRKRBs38R17R60a2Wxn+AOWNl0S0w5SSb/Nm/8LtXoQumTAXEGUC6JsKfzzHHeLx0gecxceHurpvyBuv6WjX1RL5nAPGe5eK98Jr1fLptJs2CvVBSQbdNXVMAERGRWlUbAeSf4+H01jBlRO20yeKooOvFYm9/hybmmBGL95iWqFB3KPEOCkNSzDEs57Qzx3psuBtGtKMMa3O6cgOIjwpIej4cyi7/PXgPsrUCiH2H3ON5ZggJFK2EKiIitcr+hVnZQajezu/o3pDN35pEwnW9zTEXLaLhvA7mLrpQtgICZhVkT0bZQaj3DoXbBrj/BuUFjDZx5qBQ70GoFp8b/OWby7zbjWwHtw8wQ98vuz2f8xVAHhpedpCtPymAiIhIrarOINT65jnbqq2TBtsCiI/3c0Ybc9+aPs3LPleZAGYNRK1KF0y6VxcMwIBkOMtZYVl12PO5/GJz4KoVQEa0hfuGnrxtdUldMCIiUquqOwi1vuqXbK7J8Zte0D6h7PPPnQur7nB3pVTVQOfGfJ2a+H7eVxdMWk7ZfWYG2jb48w4tBuZuulYAOdmeMv7QCP7TEBGR+iQuHLolQlFJ+dvONzS/Pa385xyOmgWtC7uYIad1rO/nff0Ntxwv+1j/5Ipfk18CR5w7DDevYCVYf1EAERGRWhXkgJnXmv/qDlad/aQcDs+1QrzFhpvLutuWAXF1CbWPdwa+Zp6hw1fVJKvAXQGpreXta0IBREREal1oLa7fcaoLcpghJNO2gZ215PrNA+CmfmVfYw8jUaHmomUbj9SvLhhlUxERkXrO12JkCRFwdU/fx9sDyJAU83ZtWv2qgCiAiIiI1HO+xnTc2Nf3tGDw7IIZ7Awgaw7BIWcAaaEAIiIiIifjHUDCg2Gij64XS0wYXN4dxnU2p9wCLNlvTscNdkCrcga8+pPGgIiIiNRz9orGuM7mDrnNTjKT5e+jzduCYggNgoIS837ruPoxRkcBREREpJ6zV0BeuqBqK8yGh5izZNanmffbxddu26pLXTAiIiL1nBVAgqq55khf2yqt7RJqpUk1pgAiIiJSz1ldMNGhldtQz1vfFu7fVQERERGRSrEqINFh1Xu9PYD4Wk4+EBRARERE6jl7BaQ6ujZ1bwzYsZw9Z/xNg1BFRETquS5NzdvyNqw7mdBgeHUsHMyq/jlqmwKIiIhIPdc1EeZOrNkCYud3rL321AYFEBERkQagvozdqC0aAyIiIiJ+pwAiIiIifqcAIiIiIn6nACIiIiJ+pwAiIiIifqcAIiIiIn6nACIiIiJ+pwAiIiIifqcAIiIiIn6nACIiIiJ+pwAiIiIifqcAIiIiIn6nACIiIiJ+pwAiIiIifhcS6AbUN4ZhAJCZmRngloiIiDQs1nen9V1aEQUQL1lZWQC0adMmwC0RERFpmLKysoiPj6/wGIdRmZhyCiktLeXAgQPExsbicDhq5ZyZmZm0adOGvXv3EhcXVyvnlNqhz6Z+0udSP+lzqZ/q0+diGAZZWVmkpKQQFFTxKA9VQLwEBQXRunXrOjl3XFxcwP/jEN/02dRP+lzqJ30u9VN9+VxOVvmwaBCqiIiI+J0CiIiIiPidAogfhIeHM2XKFMLDwwPdFPGiz6Z+0udSP+lzqZ8a6ueiQagiIiLid6qAiIiIiN8pgIiIiIjfKYCIiIiI3ymAiIiIiN8pgPjB1KlTad++PREREQwbNoylS5cGukmN2rx58xg/fjwpKSk4HA6+/PJLj+cNw+DJJ5+kZcuWREZGMmrUKLZu3epxzPHjx5kwYQJxcXEkJCRw6623kp2d7cd30fg899xzDBkyhNjYWJo3b86ll17K5s2bPY7Jz89n0qRJJCYmEhMTwxVXXMHhw4c9jtmzZw8XXnghUVFRNG/enN/97ncUFxf78600Km+88QZ9+/Z1LWI1fPhwvvvuO9fz+kwC7/nnn8fhcPDAAw+4HmsMn4sCSB375JNPePDBB5kyZQorV66kX79+jB49mrS0tEA3rdHKycmhX79+TJ061efz//d//8crr7zCm2++yZIlS4iOjmb06NHk5+e7jpkwYQIbNmxg9uzZzJgxg3nz5nHHHXf46y00SnPnzmXSpEksXryY2bNnU1RUxAUXXEBOTo7rmN/+9rd88803fPrpp8ydO5cDBw5w+eWXu54vKSnhwgsvpLCwkIULF/Kvf/2LadOm8eSTTwbiLTUKrVu35vnnn2fFihUsX76cc889l0suuYQNGzYA+kwCbdmyZbz11lv07dvX4/FG8bkYUqeGDh1qTJo0yXW/pKTESElJMZ577rkAturUARjTp0933S8tLTWSk5ONF154wfVYenq6ER4ebnz00UeGYRjGxo0bDcBYtmyZ65jvvvvOcDgcxv79+/3W9sYuLS3NAIy5c+cahmF+DqGhocann37qOiY1NdUAjEWLFhmGYRjffvutERQUZBw6dMh1zBtvvGHExcUZBQUF/n0DjViTJk2Mf/7zn/pMAiwrK8vo0qWLMXv2bGPkyJHG/fffbxhG4/nfiiogdaiwsJAVK1YwatQo12NBQUGMGjWKRYsWBbBlp66dO3dy6NAhj88kPj6eYcOGuT6TRYsWkZCQwODBg13HjBo1iqCgIJYsWeL3NjdWGRkZADRt2hSAFStWUFRU5PHZdO/enbZt23p8Nn369KFFixauY0aPHk1mZqbrX+xSfSUlJXz88cfk5OQwfPhwfSYBNmnSJC688EKPvz80nv+taDO6OnT06FFKSko8/gMAaNGiBZs2bQpQq05thw4dAvD5mVjPHTp0iObNm3s8HxISQtOmTV3HSM2UlpbywAMPcMYZZ9C7d2/A/LuHhYWRkJDgcaz3Z+Prs7Oek+pZt24dw4cPJz8/n5iYGKZPn07Pnj1ZvXq1PpMA+fjjj1m5ciXLli0r81xj+d+KAoiI+N2kSZNYv349v/76a6CbIkC3bt1YvXo1GRkZfPbZZ0ycOJG5c+cGulmnrL1793L//fcze/ZsIiIiAt2cOqMumDrUrFkzgoODy4xMPnz4MMnJyQFq1anN+rtX9JkkJyeXGSRcXFzM8ePH9bnVgsmTJzNjxgzmzJlD69atXY8nJydTWFhIenq6x/Hen42vz856TqonLCyMzp07M2jQIJ577jn69evHP/7xD30mAbJixQrS0tIYOHAgISEhhISEMHfuXF555RVCQkJo0aJFo/hcFEDqUFhYGIMGDeKnn35yPVZaWspPP/3E8OHDA9iyU1eHDh1ITk72+EwyMzNZsmSJ6zMZPnw46enprFixwnXMzz//TGlpKcOGDfN7mxsLwzCYPHky06dP5+eff6ZDhw4ezw8aNIjQ0FCPz2bz5s3s2bPH47NZt26dR0CcPXs2cXFx9OzZ0z9v5BRQWlpKQUGBPpMAOe+881i3bh2rV692/QwePJgJEya4fm8Un0ugR8E2dh9//LERHh5uTJs2zdi4caNxxx13GAkJCR4jk6V2ZWVlGatWrTJWrVplAMZLL71krFq1yti9e7dhGIbx/PPPGwkJCcZXX31lrF271rjkkkuMDh06GHl5ea5zjBkzxhgwYICxZMkS49dffzW6dOliXHvttYF6S43C3XffbcTHxxu//PKLcfDgQddPbm6u65i77rrLaNu2rfHzzz8by5cvN4YPH24MHz7c9XxxcbHRu3dv44ILLjBWr15tfP/990ZSUpLx2GOPBeItNQqPPvqoMXfuXGPnzp3G2rVrjUcffdRwOBzGDz/8YBiGPpP6wj4LxjAax+eiAOIHr776qtG2bVsjLCzMGDp0qLF48eJAN6lRmzNnjgGU+Zk4caJhGOZU3CeeeMJo0aKFER4ebpx33nnG5s2bPc5x7Ngx49prrzViYmKMuLg44+abbzaysrIC8G4aD1+fCWC8//77rmPy8vKMe+65x2jSpIkRFRVlXHbZZcbBgwc9zrNr1y5j7NixRmRkpNGsWTPjoYceMoqKivz8bhqPW265xWjXrp0RFhZmJCUlGeedd54rfBiGPpP6wjuANIbPxWEYhhGY2ouIiIicqjQGRERERPxOAURERET8TgFERERE/E4BRERERPxOAURERET8TgFERERE/E4BRERERPxOAURERET8TgFERGpVTk4Of/nLXxg4cCAxMTGEh4fTunVrzjrrLB577DG2b9/uOrZ9+/a0b98+cI0VkYAJCXQDRKTxyMrK4swzz2Tt2rV07tyZ66+/nsTERI4ePcrSpUt5/vnn6dSpE506dQp0U0UkwBRARKTWvPzyy6xdu5bbbruNt99+G4fD4fH8zp07KSgoCFDrRKQ+UReMiNSaRYsWATBp0qQy4QOgQ4cOdO/enV27duFwONi9eze7d+/G4XC4fp566imP18ybN4/x48fTrFkzwsPD6dKlC48//ji5ubkex/3yyy+u1//666+cffbZxMbGkpCQwBVXXMG2bdvKtGfr1q3cfPPNdOjQgfDwcJo2bUq/fv144IEH0DZZInVLFRARqTWJiYkAbNmyhf79+5d7XEJCAlOmTOHll18G4IEHHnA9d/bZZ7t+f+ONN5g0aRIJCQmMHz+e5s2bs3z5cv785z8zZ84c5syZQ1hYmMe5Fy9ezHPPPceYMWO499572bBhA9OnT2f+/PksXryYjh07AnDgwAGGDh1KTk4OF154Iddccw05OTls3bqV119/nRdffJGQEP1fpEidCfBuvCLSiHz11VcGYMTGxhoPPfSQMWvWLOPo0aPlHt+uXTujXbt2Pp/bsGGDERISYvTr16/MOZ577jkDMF588UXXY3PmzDEAAzDefPNNj+PffPNNAzAuuugi12OvvPKKARgvv/xymWsfO3asMm9XRGpAXTAiUmsuvvhi/va3v2EYBn/7298YPXo0zZo1o3PnzkyePJmtW7dW+lxvvfUWxcXFvPrqq67KiuX3v/89SUlJfPTRR2Ve17VrV26//XaPx26//Xa6dOnCzJkzOXLkiMdzkZGRZc7RtGnTSrdTRKrHYRjq6BSR2pWVlcX333/PwoULWb58OUuWLKGoqIiIiAg++eQTLr74YgDXFNxdu3aVOcewYcNYunQpf/zjH312hbzzzjtkZGSQnZ0NmGNAzjnnHG6++Wbee++9MsfffPPNTJs2jdmzZzNq1Ch27dpF7969KSgo4PLLL2fMmDGMHDnS1UUjInVLHZwiUutiY2O56qqruOqqqwDIyMjgD3/4A6+//jq33nor+/fvLzN2w9vx48cB+POf/1yla7do0aLCxzMyMgAz/CxevJinnnqKb7/9lv/9738AdO/enWeeecbVdhGpG+qCEZE6Fx8fz2uvvUa7du04evQo69atO+lr4uLiAMjMzMQwjHJ/vB0+fNjn+azH4+PjXY/17t2bzz77jOPHj7No0SKefPJJDh06xDXXXMOCBQuq81ZFpJIUQETELxwOB9HR0R6PBQcHU1JS4vP4YcOGAeaslqpYsGABpaWlHo+VlpaycOFCHA4H/fr1K/Oa0NBQTjvtNJ5++mleeeUVDMNgxowZVbquiFSNAoiI1Jq33nqLZcuW+Xzuyy+/JDU1lYSEBHr37g2Ygz2PHj1Kfn5+mePvueceQkJCuPfee9mzZ0+Z59PT01m1alWZx7ds2cI777zj8dg777zDli1buPDCC0lKSgJgxYoVZGZmlnm9VSmJiIg4ybsVkZrQGBARqTXfffcdd911F507d+aMM84gJSWFnJwcVq1axfz58wkKCuL1118nPDwcgHPPPZfly5czduxYzjrrLMLCwhgxYgQjRoygd+/evP7669x9991069aNcePG0alTJ7KystixYwdz587lpptu4s033/Row+jRo7nvvvv49ttv6dWrFxs2bOCbb76hWbNm/OMf/3Ad98EHH/DWW28xYsQIOnXqRFxcHBs3buTbb7+ladOm3HzzzX7924mccgI0/VdEGqFNmzYZ//d//2ecf/75RocOHYyIiAgjIiLC6NSpkzFx4kRj+fLlHsdnZWUZt99+u9GyZUsjODjYAIwpU6Z4HLN06VLjN7/5jZGSkmKEhoYazZo1MwYOHGg8+uijRmpqqus4ax2QKVOmGPPnzzdGjhxpREdHG3FxccZll11mbN261eO8ixcvNu68806jd+/eRkJCghEZGWl06dLFmDx5srF79+46+xuJiEnTcEWkUbCm4U6ZMqXMcu4iUv9oDIiIiIj4nQKIiIiI+J0CiIiIiPidxoCIiIiI36kCIiIiIn6nACIiIiJ+pwAiIiIifqcAIiIiIn6nACIiIiJ+pwAiIiIifqcAIiIiIn6nACIiIiJ+pwAiIiIifvf/HiFsb0QDLsAAAAAASUVORK5CYII=\n"
},
"metadata": {}
}
],
"source": [
"data = pd.read_csv(f'logs_csv/lightning_logs/version_{csv_logger.version}/metrics.csv')\n",
"fig, ax = plt.subplots(figsize=(6,5))\n",
"x = data['epoch'][~data['epoch'].isnull()]\n",
"y = data['train_loss'][~data['train_loss'].isnull()]\n",
"print(len(y))\n",
"plt.semilogy(y, label='Training Loss',color='dodgerblue')\n",
"y = data['val_loss'][~data['val_loss'].isnull()]\n",
"print(len(y))\n",
"plt.semilogy(y, label='Validation Loss',color='k')\n",
"plt.xlabel('Steps',size=14)\n",
"plt.ylabel('Loss',size=14)\n",
"plt.legend()"
]
}
],
"metadata": {
"accelerator": "GPU",
"colab": {
"provenance": [],
"include_colab_link": true
},
"kernelspec": {
"display_name": "Python 3",
"name": "python3"
},
"language_info": {
"name": "python"
},
"gpuClass": "standard"
},
"nbformat": 4,
"nbformat_minor": 0
}
"
]
},
{
"cell_type": "code",
"source": [
"from IPython.display import HTML\n",
"\n",
"HTML(f\"\"\"\"\"\")"
],
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 321
},
"id": "ljBOLgk-wLWI",
"outputId": "c8595e33-a151-42a8-dc40-29973771c800"
},
"execution_count": 1,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
""
],
"text/html": [
""
]
},
"metadata": {},
"execution_count": 1
}
]
},
{
"cell_type": "markdown",
"source": [
"## Importing PyTorch Lightning and Libraries\n",
"We will first install PyTorch Lightning and import libraries needed to train our machine learning models."
],
"metadata": {
"id": "BPuN7hFOFT5L"
}
},
{
"cell_type": "code",
"source": [
"%%capture\n",
"!pip install pytorch-lightning > /dev/null\n",
"import math\n",
"import numpy as np\n",
"from typing import Sequence, Tuple\n",
"\n",
"import torch\n",
"import torch.nn as nn\n",
"import torch.nn.functional as F\n",
"from torch import Tensor\n",
"\n",
"from torch.utils.data import TensorDataset, DataLoader, random_split\n",
"import pytorch_lightning as pl\n",
"from pytorch_lightning import loggers as pl_loggers"
],
"metadata": {
"id": "fPn6Q6URnYDN"
},
"execution_count": 2,
"outputs": []
},
{
"cell_type": "markdown",
"source": [
"## Defining Symmetry Functions\n",
"\n",
"We will define the BP and ANI symmetry functions to ensure that our ML predictions are invariant to translations, rotations, and permutations.\n",
"\n",
"- **pairwise_vector:** Distance function for calculating distances between each atom.\n",
"\n",
"- **symmetry_function_g1:** BP radial symmetry function.\n",
"\n",
"- **symmetry_function_g2:** BP angular symmetry function.\n",
"\n",
"- **symmetry_function_g2ani:** ANI angular symmetry function.\n"
],
"metadata": {
"id": "VbFZM9qAsPwK"
}
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {
"id": "tzRTvSuqsPwM"
},
"outputs": [],
"source": [
"def pairwise_vector(coords: Tensor) -> Tensor:\n",
" num_batches, num_channels, _ = coords.size()\n",
" rij = coords[:, :, None] - coords[:, None]\n",
" mask = ~torch.eye(num_channels, dtype=torch.bool, device=coords.device) # remove self-interaction\n",
" rij = torch.masked_select(rij, mask.unsqueeze(2)).view(num_batches, num_channels, num_channels - 1, 3)\n",
" return rij\n",
"\n",
"\n",
"def symmetry_function_g1(rij: Tensor, Rcr: float, EtaR: Tensor, ShfR: Tensor) -> Tensor:\n",
" dij = torch.norm(rij, dim=3)\n",
" fij = (torch.cos(dij / Rcr * math.pi) + 1) * 0.5 * (dij <= Rcr)\n",
" g1 = torch.sum(torch.exp(-EtaR.unsqueeze(dim=1) * (dij.unsqueeze(dim=-1) - ShfR.unsqueeze(dim=1))**2) * fij.unsqueeze(dim=-1), dim=2)\n",
" return g1\n",
"\n",
"\n",
"def symmetry_function_g2(rij: Tensor, Rca: float, Zeta: Tensor, EtaA: Tensor, LamA: Tensor) -> Tensor:\n",
" c = torch.combinations(torch.arange(rij.size(2)), r=2)\n",
" rij = rij[:, :, c]\n",
" r12 = rij[:, :, :, 0]\n",
" r13 = rij[:, :, :, 1]\n",
" r23 = r12 - r13\n",
" d12 = torch.norm(r12, dim=3)\n",
" d13 = torch.norm(r13, dim=3)\n",
" d23 = torch.norm(r23, dim=3)\n",
" f12 = (torch.cos(d12 / Rca * math.pi) + 1) * 0.5\n",
" f13 = (torch.cos(d13 / Rca * math.pi) + 1) * 0.5\n",
" f23 = (torch.cos(d23 / Rca * math.pi) + 1) * 0.5\n",
" cosine = torch.einsum('ijkl,ijkl->ijk', r12, r13) / (d12 * d13)\n",
"\n",
" g2 = torch.sum(2**(1 - Zeta.unsqueeze(dim=1)) * (1 + LamA.unsqueeze(dim=1) * cosine.unsqueeze(dim=-1))**Zeta.unsqueeze(dim=1) * torch.exp(-EtaA.unsqueeze(dim=1) * (d12**2 + d13**2 + d23**2).unsqueeze(dim=-1)) * (f12 * f13 * f23).unsqueeze(dim=-1), dim=2)\n",
" return g2\n",
"\n",
"\n",
"def symmetry_function_g2ani(rij: Tensor, Rca: float, Zeta: Tensor, ShfZ: Tensor, EtaA: Tensor, ShfA: Tensor) -> Tensor:\n",
" c = torch.combinations(torch.arange(rij.size(2)), r=2)\n",
" rij = rij[:, :, c]\n",
" r12 = rij[:, :, :, 0]\n",
" r13 = rij[:, :, :, 1]\n",
" r23 = r12 - r13\n",
" d12 = torch.norm(r12, dim=3)\n",
" d13 = torch.norm(r13, dim=3)\n",
" f12 = (torch.cos(d12 / Rca * math.pi) + 1) * 0.5\n",
" f13 = (torch.cos(d13 / Rca * math.pi) + 1) * 0.5\n",
" cosine = torch.einsum('ijkl,ijkl->ijk', r12, r13) / (d12 * d13)\n",
" cosine = torch.cos(torch.acos(cosine).unsqueeze(dim=-1) - ShfA.unsqueeze(dim=1))\n",
"\n",
" g2 = torch.sum(2**(1 - Zeta.unsqueeze(dim=1)) * (1 + cosine)**Zeta.unsqueeze(dim=1) * torch.exp(-EtaA.unsqueeze(dim=1) * (0.5 * (d12 + d13).unsqueeze(dim=-1) - ShfZ.unsqueeze(dim=1))**2) * (f12 * f13).unsqueeze(dim=-1), dim=2)\n",
" return g2"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "826_ckjtgmp2"
},
"source": [
"## Defining Neural Network and Feature Extraction Classes\n",
"\n",
"We will now define feature extraction classes which will be used in our Behler-Parrinello and ANI neural networks.\n"
]
},
{
"cell_type": "markdown",
"metadata": {
"id": "oCSkqkOrgmp2"
},
"source": [
"### Defining Sequential and Dense Classes\n",
"\n",
"The Sequential class contains the function for the feed-forward aspect of our neural network.\n",
"The Dense class contains functions to describe a densely connected neural network."
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {
"id": "WXspRElYvr5n"
},
"outputs": [],
"source": [
"class Sequential(nn.Sequential):\n",
" def forward(self, input: Tuple[Tensor, Tensor]) -> Tuple[Tensor, Tensor]:\n",
" for module in self:\n",
" input = module(input)\n",
" return input\n",
"\n",
"class Dense(nn.Module):\n",
" def __init__(self, num_channels: int, in_features: int, out_features: int, bias: bool = True, activation: bool = False, residual: bool = False) -> None:\n",
" super().__init__()\n",
" self.num_channels = num_channels\n",
" self.in_features = in_features\n",
" self.out_features = out_features\n",
" self.weight = nn.Parameter(torch.Tensor(num_channels, out_features, in_features))\n",
" if bias:\n",
" self.bias = nn.Parameter(torch.Tensor(num_channels, out_features))\n",
" else:\n",
" self.register_parameter('bias', None)\n",
" self.activation = activation\n",
" self.residual = residual\n",
" self.reset_parameters()\n",
"\n",
" def reset_parameters(self) -> None:\n",
" for w in self.weight:\n",
" nn.init.kaiming_uniform_(w, a=math.sqrt(5))\n",
" if self.bias is not None:\n",
" for b, w in zip(self.bias, self.weight):\n",
" fan_in, _ = nn.init._calculate_fan_in_and_fan_out(w)\n",
" bound = 1 / math.sqrt(fan_in)\n",
" nn.init.uniform_(b, -bound, bound)\n",
"\n",
" def forward(self, input: Tuple[Tensor, Tensor]) -> Tuple[Tensor, Tensor]:\n",
" x, channels = input\n",
" weight: Tensor = self.weight[channels]\n",
" output: Tensor = torch.bmm(x.transpose(0, 1), weight.transpose(1, 2)).transpose(0, 1)\n",
"\n",
" if self.bias is not None:\n",
" bias = self.bias[channels]\n",
" output = output + bias\n",
"\n",
" if self.activation:\n",
" output = torch.tanh(output)\n",
"\n",
" if self.residual:\n",
" if output.shape[2] == x.shape[2]:\n",
" output = output + x\n",
" elif output.shape[2] == x.shape[2] * 2:\n",
" output = output + torch.cat([x, x], dim=2)\n",
" else:\n",
" raise NotImplementedError(\"Not implemented\")\n",
"\n",
" return output, channels\n",
"\n",
" def extra_repr(self) -> str:\n",
" return 'num_channels={}, in_features={}, out_features={}, bias={}, activation={}, residual={}'.format(\n",
" self.num_channels, self.in_features, self.out_features, self.bias is not None, self.activation, self.residual\n",
" )"
]
},
{
"cell_type": "markdown",
"source": [
"### Defining the BP Feature Class\n",
"\n",
"Now we will create the feature class, which takes input information and uses functions to extract characteristics unique to the called input features. Here we will be using the previously defined symmetry functions for feature extraction.\n"
],
"metadata": {
"id": "SUdKJjQLK4Wz"
}
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {
"id": "rRXofpIJkKnd"
},
"outputs": [],
"source": [
"class Feature(nn.Module):\n",
" def __init__(self, Rcr: float, EtaR: Tensor, ShfR: Tensor, Rca: float, Zeta: Tensor, EtaA: Tensor, LamA: Tensor) -> None:\n",
" super().__init__()\n",
" assert len(EtaR) == len(ShfR) == len(LamA)\n",
" assert len(Zeta) == len(EtaA)\n",
" self.Rcr = Rcr\n",
" self.Rca = Rca\n",
" self.EtaR = torch.Tensor(EtaR)\n",
" self.ShfR = torch.Tensor(ShfR)\n",
" self.Zeta = torch.Tensor(Zeta)\n",
" self.EtaA = torch.Tensor(EtaA)\n",
" self.LamA = torch.Tensor(LamA)\n",
"\n",
" def forward(self, coords: Tensor, atom_types: Tensor) -> Tensor:\n",
" num_batches, num_channels, _ = coords.size()\n",
" rij = pairwise_vector(coords)\n",
" EtaR = self.EtaR.to(device=coords.device)[atom_types]\n",
" ShfR = self.ShfR.to(device=coords.device)[atom_types]\n",
" Zeta = self.Zeta.to(device=coords.device)[atom_types]\n",
" EtaA = self.EtaA.to(device=coords.device)[atom_types]\n",
" LamA = self.LamA.to(device=coords.device)[atom_types]\n",
" g1 = symmetry_function_g1(rij, self.Rcr, EtaR, ShfR)\n",
" g2 = symmetry_function_g2(rij, self.Rca, Zeta, EtaA, LamA)\n",
"\n",
" return torch.concat((g1, g2), dim=2)\n",
"\n",
" @property\n",
" def output_length(self) -> int:\n",
" return len(self.EtaR[0]) + len(self.EtaA[0])"
]
},
{
"cell_type": "markdown",
"source": [
"### Defining the ANI Feature Class\n",
"\n",
"We will create a similar feature class for ANI that uses the ANI angle symmetry function.\n"
],
"metadata": {
"id": "id6zvxx-K_yu"
}
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {
"id": "st4TXB2yeW6v"
},
"outputs": [],
"source": [
"class FeatureANI(nn.Module):\n",
" def __init__(self, Rcr: float, EtaR: Tensor, ShfR: Tensor, Rca: float, Zeta: Tensor, ShfZ: Tensor, EtaA: Tensor, ShfA: Tensor) -> None:\n",
" super().__init__()\n",
" assert len(EtaR) == len(ShfR)\n",
" assert len(Zeta) == len(ShfZ) == len(EtaA) == len(ShfA)\n",
" self.Rcr = Rcr\n",
" self.Rca = Rca\n",
" self.EtaR = torch.Tensor(EtaR)\n",
" self.ShfR = torch.Tensor(ShfR)\n",
" self.Zeta = torch.Tensor(Zeta)\n",
" self.ShfZ = torch.Tensor(ShfZ)\n",
" self.EtaA = torch.Tensor(EtaA)\n",
" self.ShfA = torch.Tensor(ShfA)\n",
"\n",
" def forward(self, coords: Tensor, atom_types: Tensor) -> Tensor:\n",
" num_batches, num_channels, _ = coords.size()\n",
" rij = pairwise_vector(coords)\n",
" EtaR = self.EtaR.to(device=coords.device)[atom_types]\n",
" ShfR = self.ShfR.to(device=coords.device)[atom_types]\n",
" Zeta = self.Zeta.to(device=coords.device)[atom_types]\n",
" ShfZ = self.ShfZ.to(device=coords.device)[atom_types]\n",
" EtaA = self.EtaA.to(device=coords.device)[atom_types]\n",
" ShfA = self.ShfA.to(device=coords.device)[atom_types]\n",
" g1 = symmetry_function_g1(rij, self.Rcr, EtaR, ShfR)\n",
" g2 = symmetry_function_g2ani(rij, self.Rca, Zeta, ShfZ, EtaA, ShfA)\n",
"\n",
" return torch.concat((g1, g2), dim=2)\n",
"\n",
" @property\n",
" def output_length(self) -> int:\n",
" return len(self.EtaR[0]) + len(self.EtaA[0])"
]
},
{
"cell_type": "markdown",
"source": [
"### Creating the Fitting Neural Network\n",
"\n",
"Now we create the Fitting class, which will use the dense neural network for fitting.\n"
],
"metadata": {
"id": "YJsBu7NoLFzC"
}
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {
"id": "02e3WPabvjIl"
},
"outputs": [],
"source": [
"class Fitting(nn.Module):\n",
" def __init__(self, n_types: int, in_features: int, neuron: Sequence[int] = [240, 240, 240]) -> None:\n",
" super().__init__()\n",
" layers = [Dense(n_types, in_features, neuron[0], activation=True)]\n",
" for i in range(len(neuron)-1):\n",
" layers.append(Dense(n_types, neuron[i], neuron[i+1], activation=True, residual=True))\n",
" layers.append(Dense(n_types, neuron[-1], 1))\n",
" self.fitting_net = Sequential(*layers)\n",
"\n",
" def forward(self, input : Tuple[Tensor, Tensor]) -> Tensor:\n",
" output, _ = self.fitting_net(input)\n",
" return output"
]
},
{
"cell_type": "markdown",
"source": [
"### The Behler-Parrinello Fitting Neural Network (BP-FNN)\n",
"\n",
"We create the BPNN class that can be used for feature extraction with the symmetry functions.\n"
],
"metadata": {
"id": "7YTxfJXgLKsy"
}
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {
"id": "Gw-8zbn_wPz5"
},
"outputs": [],
"source": [
"class BPNN(pl.LightningModule):\n",
" def __init__(self, descriptor: nn.Module, fitting_net: nn.Module, learning_rate=5e-4) -> None:\n",
" super().__init__()\n",
" self.descriptor = descriptor\n",
" self.fitting_net = fitting_net\n",
" self.learning_rate = learning_rate\n",
"\n",
" def forward(self, coords: torch.Tensor, atom_types: torch.Tensor):\n",
" coords.requires_grad_()\n",
" descriptors = self.descriptor(coords, atom_types)\n",
" atomic_energies = self.fitting_net((descriptors, atom_types))\n",
" energy = torch.unbind(torch.sum(atomic_energies, dim=1))\n",
" gradient, = torch.autograd.grad(energy, [coords], create_graph=True)\n",
" return torch.hstack(energy), gradient\n",
"\n",
" def training_step(self, batch, batch_idx):\n",
" qm_coord, atom_types, energy, gradient = batch\n",
" ene_pred, grad_pred = self(qm_coord, atom_types[0])\n",
" ene_loss = F.mse_loss(ene_pred, energy)\n",
" grad_loss = F.mse_loss(grad_pred, gradient)\n",
"\n",
" lr = self.optimizers().optimizer.param_groups[0]['lr']\n",
" start_lr = self.optimizers().optimizer.param_groups[0]['initial_lr']\n",
" w_ene = 1\n",
" w_grad = 1 + 99 * (lr / start_lr)\n",
"\n",
" loss = w_ene / (w_ene + w_grad) * ene_loss + w_grad / (w_ene + w_grad) * grad_loss\n",
" self.log('train_loss', loss)\n",
" self.log('l2_trn', torch.sqrt(loss))\n",
" self.log('l2_e_trn', torch.sqrt(ene_loss))\n",
" self.log('l2_f_trn', torch.sqrt(grad_loss))\n",
" return loss\n",
"\n",
" def validation_step(self, batch, batch_idx):\n",
" torch.set_grad_enabled(True)\n",
" qm_coord, atom_types, energy, gradient = batch\n",
" ene_pred, grad_pred = self(qm_coord, atom_types[0])\n",
" ene_loss = F.mse_loss(ene_pred, energy)\n",
" grad_loss = F.mse_loss(grad_pred, gradient)\n",
"\n",
" lr = self.optimizers().optimizer.param_groups[0]['lr']\n",
" start_lr = self.optimizers().optimizer.param_groups[0]['initial_lr']\n",
" w_ene = 1\n",
" w_grad = 1 + 99 * (lr / start_lr)\n",
"\n",
" loss = w_ene / (w_ene + w_grad) * ene_loss + w_grad / (w_ene + w_grad) * grad_loss\n",
" self.log('val_loss', loss)\n",
" self.log('l2_tst', torch.sqrt(loss))\n",
" self.log('l2_e_tst', torch.sqrt(ene_loss))\n",
" self.log('l2_f_tst', torch.sqrt(grad_loss))\n",
" self.log('lr', lr)\n",
" return loss\n",
"\n",
" def configure_optimizers(self):\n",
" optimizer = torch.optim.Adam(self.parameters(), lr=self.learning_rate)\n",
" scheduler = {'scheduler': torch.optim.lr_scheduler.ExponentialLR(optimizer, 0.95),\n",
" 'interval': 'epoch',\n",
" 'frequency': 10,\n",
" }\n",
" return [optimizer], [scheduler]"
]
},
{
"cell_type": "markdown",
"source": [
"## Importing Data and Seeding\n",
"\n",
"We will now import our semiempirical and DFT calculation data. We will then use seeding to generate random but reproducible training."
],
"metadata": {
"id": "-7Tv-R5NJSuF"
}
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {
"id": "vuHEYr6CCf5u"
},
"outputs": [],
"source": [
"ds = np.DataSource(None)\n",
"qm_coord = np.array(np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_coord.npy\", \"rb\")), dtype=\"float32\")\n",
"atom_types = np.loadtxt(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_elem.txt\", \"r\"), dtype=int)\n",
"elems = np.unique(atom_types).tolist()\n",
"atom_types = np.array([[elems.index(i) for i in atom_types]])\n",
"atom_types = atom_types.repeat(len(qm_coord), axis=0)\n",
"\n",
"energy = np.array((np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy.npy\", \"rb\")) - np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy_sqm.npy\", \"rb\"))) * 27.2114 * 23.061, dtype=\"float32\")\n",
"energy = energy - energy.mean()\n",
"qm_gradient = np.array((np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad.npy\", \"rb\")) - np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad_sqm.npy\", \"rb\"))) * 27.2114 * 23.061 / 0.529177249, dtype=\"float32\")\n",
"\n",
"device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')\n",
"\n",
"qm_coord = torch.from_numpy(qm_coord).to(device)\n",
"atom_types = torch.from_numpy(atom_types).to(device)\n",
"energy = torch.from_numpy(energy).to(device)\n",
"qm_gradient = torch.from_numpy(qm_gradient).to(device)"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {
"id": "5fc0zx5YOn-y",
"colab": {
"base_uri": "https://localhost:8080/"
},
"outputId": "3a6bbd16-ac1c-47d3-99fb-75011e5df388"
},
"outputs": [
{
"output_type": "stream",
"name": "stderr",
"text": [
"INFO:lightning_fabric.utilities.seed:Global seed set to 2\n"
]
}
],
"source": [
"pl.seed_everything(2)\n",
"dataset = TensorDataset(qm_coord, atom_types, energy, qm_gradient)\n",
"train, val = random_split(dataset, [2016, 84])\n",
"# Training Set Size: 2016 (96%)\n",
"# Test Set Size: 84 ( 4%)\n",
"# Data Set Size: 2100\n",
"train_loader = DataLoader(train, batch_size=32)\n",
"val_loader = DataLoader(val, batch_size=32)"
]
},
{
"cell_type": "markdown",
"source": [
"## Using ANI for Feature Extraction\n",
"\n",
"Here we set the parameters for the ANI model and begin training our BP-FNN."
],
"metadata": {
"id": "L-g9rxO6LSu5"
}
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {
"id": "0FYCh2Le7jRr",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 306
},
"outputId": "6af9d322-d0f6-41d4-c2d9-4b99008fc1b4"
},
"outputs": [
{
"output_type": "stream",
"name": "stderr",
"text": [
"INFO:lightning_fabric.utilities.seed:Global seed set to 2\n",
"INFO:pytorch_lightning.utilities.rank_zero:GPU available: True (cuda), used: True\n",
"INFO:pytorch_lightning.utilities.rank_zero:TPU available: False, using: 0 TPU cores\n",
"INFO:pytorch_lightning.utilities.rank_zero:IPU available: False, using: 0 IPUs\n",
"INFO:pytorch_lightning.utilities.rank_zero:HPU available: False, using: 0 HPUs\n",
"INFO:pytorch_lightning.accelerators.cuda:LOCAL_RANK: 0 - CUDA_VISIBLE_DEVICES: [0]\n",
"INFO:pytorch_lightning.callbacks.model_summary:\n",
" | Name | Type | Params\n",
"-------------------------------------------\n",
"0 | descriptor | FeatureANI | 0 \n",
"1 | fitting_net | Fitting | 383 K \n",
"-------------------------------------------\n",
"383 K Trainable params\n",
"0 Non-trainable params\n",
"383 K Total params\n",
"1.532 Total estimated model params size (MB)\n",
"INFO:pytorch_lightning.utilities.rank_zero:`Trainer.fit` stopped: `max_epochs=100` reached.\n"
]
}
],
"source": [
"%%capture\n",
"%%time\n",
"pl.seed_everything(2)\n",
"\n",
"ani = True\n",
"\n",
"if ani:\n",
" # From TorchANI\n",
" Rcr = 5.2000e+00\n",
" Rca = 3.5000e+00\n",
" EtaR = [1.6000000e+01]\n",
" ShfR = [9.0000000e-01,1.1687500e+00,1.4375000e+00,1.7062500e+00,1.9750000e+00,2.2437500e+00,2.5125000e+00,2.7812500e+00,3.0500000e+00,3.3187500e+00,3.5875000e+00,3.8562500e+00,4.1250000e+00,4.3937500e+00,4.6625000e+00,4.9312500e+00]\n",
" Zeta = [3.2000000e+01]\n",
" ShfZ = [1.9634954e-01,5.8904862e-01,9.8174770e-01,1.3744468e+00,1.7671459e+00,2.1598449e+00,2.5525440e+00,2.9452431e+00]\n",
" EtaA = [8.0000000e+00]\n",
" ShfA = [9.0000000e-01,1.5500000e+00,2.2000000e+00,2.8500000e+00]\n",
" EtaR, ShfR = np.array(np.meshgrid(EtaR, ShfR)).reshape(2, -1)\n",
" Zeta, ShfZ, EtaA, ShfA = np.array(np.meshgrid(Zeta, ShfZ, EtaA, ShfA)).reshape(4, -1)\n",
" EtaR = np.repeat([EtaR], 3, axis=0)\n",
" ShfR = np.repeat([ShfR], 3, axis=0)\n",
" Zeta = np.repeat([Zeta], 3, axis=0)\n",
" ShfZ = np.repeat([ShfZ], 3, axis=0)\n",
" EtaA = np.repeat([EtaA], 3, axis=0)\n",
" ShfA = np.repeat([ShfA], 3, axis=0)\n",
" descriptor = FeatureANI(Rcr, EtaR, ShfR, Rca, Zeta, ShfZ, EtaA, ShfA)\n",
"else:\n",
" Rcr = 6.0\n",
" Rca = 6.0\n",
" ShfR = np.zeros((3,6)) # H, C, O\n",
" EtaR = [0.0, 0.04, 0.14, 0.32, 0.71, 1.79]\n",
" EtaR = np.repeat([EtaR], 3, axis=0) # H, C, O\n",
" Zeta = [1, 2, 4, 8, 16, 32, 1, 2, 4, 8, 16, 32]\n",
" Zeta = np.repeat([Zeta], 3, axis=0) # H, C, O\n",
" EtaA = [0.0, 0.04, 0.14, 0.32, 0.71, 1.79, 0.0, 0.04, 0.14, 0.32, 0.71, 1.79]\n",
" EtaA = np.repeat([EtaA], 3, axis=0) # H, C, O\n",
" LamA = [1, 1, 1, 1, 1, 1, -1, -1, -1, -1, -1, -1]\n",
" LamA = np.repeat([LamA], 3, axis=0) # H, C, O\n",
" descriptor = Feature(Rcr, EtaR, ShfR, Rca, Zeta, EtaA, LamA)\n",
"\n",
"fitting_net = Fitting(3, descriptor.output_length, neuron=[240, 240, 240])\n",
"model = BPNN(descriptor, fitting_net, learning_rate=5e-4)\n",
"csv_logger = pl_loggers.CSVLogger('logs_csv/')\n",
"trainer = pl.Trainer(max_epochs=100, logger=csv_logger, log_every_n_steps=20, accelerator='auto')\n",
"trainer.fit(model, train_loader, val_loader)\n",
"model.to(device)"
]
},
{
"cell_type": "markdown",
"source": [
"## Saving the Model with PyTorch Files and Evaluating the Model's Accuracy Using RMSD"
],
"metadata": {
"id": "OkKS46hBwoEi"
}
},
{
"cell_type": "markdown",
"source": [
"### Saving the Model with PyTorch\n",
"\n",
"The following files are saved:\n",
"\n",
"**1) model.pt**\n",
"- torch.save saves tensors to model.pt\n",
"\n",
"**2) model_script.pt**\n",
"- torch.jit.save attempts to preserve the behavior of some operators across PyTorch versions.\n",
"\n",
"Previously saved models can be loaded with:\n",
" - model.load_state_dict(torch.load(\"model.pt\"))\n",
" - torch.jit.load(\"model_script.pt\")"
],
"metadata": {
"id": "UoCqvOvdLZ6H"
}
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {
"id": "wDsRamgOkdXY"
},
"outputs": [],
"source": [
"torch.save(model.state_dict(), 'model.pt')\n",
"torch.jit.save(model.to_torchscript(), \"model_script.pt\")"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {
"id": "cRMmWy9TPeJD"
},
"outputs": [],
"source": [
"ene_pred, grad_pred = model(qm_coord, atom_types[0])"
]
},
{
"cell_type": "markdown",
"source": [
"### Plotting RMSD for $\\Delta$MLP Energy and Forces\n",
"\n",
"RMSD for predicted and reference energy and forces are calculated and displayed below."
],
"metadata": {
"id": "qnQCBYPZL7eF"
}
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {
"id": "JlF1V44dPibM",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 506
},
"outputId": "d302ce14-9d13-4bec-fdb8-adb38f037330"
},
"outputs": [
{
"output_type": "display_data",
"data": {
"text/plain": [
""
],
"image/png": "iVBORw0KGgoAAAANSUhEUgAAA94AAAHpCAYAAAB0jeQXAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAD4g0lEQVR4nOzdd3SUVbfH8e9MCJ0EQknAACIgIL0TkNACiFKko3QBQcUrRUGwggUVpNkQRZoiVRAQ6RGkGuCNoIJShUgTIhMIEEIy949xxkwySWYmZVJ+n7WyVuape7jv9WQ/zzl7G8xmsxkRERERERERyRBGTwcgIiIiIiIikpMp8RYRERERERHJQEq8RURERERERDKQEm8RERERERGRDKTEW0RERERERCQDKfEWERERERERyUBKvEVEREREREQyUB5PB5AdxMfHc/78eYoUKYLBYPB0OCIiks2ZzWauX79OmTJlMBr1DDwzaCwXEZH05sp4rsTbCefPn6ds2bKeDkNERHKYc+fOERgY6OkwcgWN5SIiklGcGc+VeDuhSJEigOUf1MfHx8PRiIhIdhcVFUXZsmVt44tkPI3lIiKS3lwZz7N14v36668zadIku21VqlTh2LFjANy+fZuxY8eydOlSYmJiaN++PR9//DH+/v4u3cc6Jc3Hx0eDtYiIpBtNec48GstFRCSjODOeZ/uFZdWrV+fChQu2n127dtn2jR49mnXr1rFixQp27NjB+fPn6datmwejFRERERERkdwmW7/xBsiTJw8BAQFJtptMJubNm8eSJUto3bo1APPnz6datWrs27ePJk2aZHaoIiIiIiIikgtl+zfex48fp0yZMtx333307duXs2fPAnDw4EFiY2MJCQmxHVu1alXKlSvH3r17U7xmTEwMUVFRdj8iIiIiIiIi7sjWiXfjxo1ZsGABGzdu5JNPPuH06dM0b96c69evc/HiRfLmzUvRokXtzvH39+fixYspXnfKlCn4+vraflQFVURERERERNyVraead+jQwfZ7rVq1aNy4MeXLl2f58uUUKFDA7etOmDCBMWPG2D5bq9WJiIiIiIiIuCpbv/FOrGjRotx///2cOHGCgIAA7ty5w7Vr1+yOuXTpksM14Qnly5fPVvU0I6ufnjlzBoPBYPfj7e3NPffcQ69evThw4IDD8wYNGmQ7/sMPP0z2+r1797Ydt2DBArt9ZrOZL7/8ktatW1O8eHHy5s2Lv78/devW5emnn2bHjh12x7/++ut2cXp5edn+vXv27Mn8+fOJjo5O87+J1c6dO3n++edp1aoVvr6+GAwGBg0a5PJ1jh8/zttvv01wcDBlypQhb968lC1blgEDBtiq3zty6NAhevbsSYUKFShQoADly5enS5cu7Ny5M8mx+/fvZ+DAgdSoUQM/Pz/y589PpUqV6N27d7L/NxQRkZxD43ny0ms8Txy3o58hQ4YkOW/jxo2EhIRQtGhRChQoQM2aNZk+fTpxcXFJjv3hhx9SvH7if3sREVdk6zfeid24cYOTJ0/Sv39/6tevj7e3N9u2baN79+4A/P7775w9e5agoCAPR2qvYsWK9OvXD4Do6GgOHjzIihUrWLNmDVu3biU4ONjheXny5OGLL75g5MiRSfZFRkby7bffkidPHu7evZtk/xNPPMGCBQsoVqwYHTt25J577uHWrVv8/PPPzJs3j6ioKFq0aJHkvO7du1OjRg3AMhPgzJkz/PDDD6xcuZJXX32VxYsX07JlyzT8a1h88cUXLFy4kIIFC1KuXDm319m/8sorLFu2jBo1atClSxd8fHw4cuQIixcvZuXKlWzcuDHJv++aNWvo3r07+fLlo2vXrpQtW5Zz586xevVq1q5dy/z58+3+aPjxxx/ZsmULTZo0oXXr1hQsWJBTp06xdu1aVqxYwcKFC+nfv39a/jlERCQb0HieVHqN5ynF8vnnn/PXX3/Rvn17u+2zZ8/mueeew8fHh27dulG0aFG2bt3K2LFj2bt3LytWrHB4vRYtWji8X506ddyKXUQEAHM2NnbsWPMPP/xgPn36tHn37t3mkJAQc4kSJcyXL182m81m84gRI8zlypUzb9++3XzgwAFzUFCQOSgoyOX7mEwmM2A2mUzpGv/p06fNgLl9+/ZJ9k2ZMsUMmIODg5PsGzhwoBkwd+rUyQyYw8PDkxwza9YsM2Du3LmzGTDPnz/ftm/nzp1mwFynTh2H3+mff/4x7969227ba6+9ZgbMX3/9dZLjb9++bX7nnXfMRqPRXKhQIfPPP//szNdPUVhYmPmXX34x371717x3714zYB44cKDL15k/f7750KFDSbZ//fXXZsD8wAMPJNlXrVo1s8FgMP/vf/+z237w4EGzwWAwV6hQwW77rVu3HN77yJEj5vz585tLlSpljo+Pdzl2Ecm5MmpckeRl5L+5xvPkpdd4npyLFy+a8+TJYy5evLg5JibGtv2vv/4y58uXz1ysWDHzmTNnbNtjY2PNXbp0cfhvEBoaagbMr732WrrFJyI5mytjS7aeah4REcFjjz1GlSpV6NWrF8WLF2ffvn2ULFkSgBkzZtCxY0e6d+9OcHAwAQEBfPPNNx6O2jnW6VIHDx5M9piBAwfi5eXFvHnzkuyztk5z9HbfWtV94MCBDqfRFy1alKZNmzoda758+Rg/fjyvvvoq0dHRvPjii06fm5wGDRpQvXp1vLy80nSdQYMGUbdu3STb+/Tpw/33389vv/3GlStX7PadOnWK0qVLJ3myXa9ePUqXLs3ff/9ttz1//vwO712jRg2qVavG5cuXVRlfRCSX0niePuN5chYuXMjdu3fp378/efPmtW3//vvviYmJYejQoZQvX962PU+ePEyaNAmATz75JENiEhFxJFsn3kuXLuX8+fPExMQQERHB0qVLqVixom1//vz5+eijj4iMjCQ6Oppvvvkm1fXdWU2ePMmvBrjnnnto164dS5Ys4c6dO7bthw4dIjw8nMGDBzs8r3jx4gD88ccf6Rrr2LFjKViwIJs2bcJkMtm2W9dMpceUtfTk7e0NJP03rlGjBhcuXCA8PNxu+6FDh7hw4QJt2rRx6vonT57k999/p2zZsvj6+qZLzCIikj1pPM8Y1ocVQ4cOtdtu7WBToUKFJOdYt+3Zs4eYmJgk+48fP87MmTOZMmUKixcv5q+//krvsEUkF8rWiXdO9vnnnwPw4IMPpnjckCFDuHr1Kt9++61t27x588iTJw8DBgxweE779u3x8fFhzpw59O3bl5UrV/Lnn3+mOebChQtTv3594uPjU3yynxX89NNP/PrrrzRs2DBJy7kZM2ZQuHBhmjZtSr9+/ZgwYQJ9+/blwQcfpGXLlsyZMyfZa77++uu89NJL9OvXz/amPbnjRUQk59N4nnF+/PFH/vjjD5o0aUL16tXt9pUoUQKA06dPJznPuu3u3bucOnUqyf4lS5YwevRoJk6cyIABA7j33nsZM2aMw4JsIiLOylHF1bKrEydO8PrrrwP/FWMJDQ3F39+fqVOnpnhu586dKVGiBF988QU9e/bk9u3bfP311zzyyCP4+/s7PCcwMJBVq1YxZMgQlixZwpIlSwAoWbIkrVq1Yvjw4bRu3dqt71KmTBkAu+nbjRo14ujRoxQsWNCta6Y3k8nEwIEDMRqNvPfee0n2N2/enB9//JGePXvy1Vdf2baXL1+eQYMGJTtr4qeffrJNXwNLz/hFixbRrl279P8SIiKS5Wg8z1zJve0GaNeunW36/rPPPmtrC3v37l27sTph95uSJUvyzjvv0LFjR+69916io6PZu3cvL774IjNmzMBgMPD+++9n7JcSkRxLb7yzgJMnTzJp0iQmTZrEtGnTCA0NJSAggF27dlGtWrUUz/X29qZfv35s3ryZv/76i9WrV/PPP//wxBNPpHheSEgIJ0+eZMuWLbzyyis8/PDDxMTEsHz5ctq0acPEiRPT7fsVLFiQqlWrUq5cuXS7prtu3bpF165dOXbsGG+88YbD6XLfffcdwcHBNGzYkKNHj3Lz5k2OHj1Ks2bNGDhwIOPGjXN47ZEjR2I2m7l58yY///wzDz30EB06dGDatGkZ/K1ERCQr0HieeaKiolixYgWFCxemd+/eSfZXqFCBiRMnEhkZSc2aNXniiScYPXo09erVY/v27bbvYDT+96dw9erVGT9+PNWrV6dQoUKUKlWKLl26EBoaSsmSJZk9ezaXL1/OtO8oIjmLEu8soH379pjNZsxmM5cvX2bq1KlcvnyZzp07c+PGjVTPf+KJJ4iPj2fBggV88cUXBAQE8PDDD6d6Xp48eQgJCWHy5Ml89913XL16lc8++4w8efIwZcoUDh065PJ3OX/+PICtwF1Wcvv2bdsAOmHCBId/jFy9epW+fftSuXJlFi9eTNWqVSlQoABVq1Zl8eLF1K9fn+nTp3P27Nlk71OgQAFq1arFggULeOihhxg/fjy//PJLRn41EckkEZgI5TQRmFI/WHIdjeeZZ+nSpdy8eZPevXtTuHBhh8dMnjyZxYsXU6VKFZYuXcq8efMIDAxk9+7dtmJ0pUqVSvVeAQEBdOnShbt377J///50/R4i4hmeGM+VeGcxJUuW5Pnnn2fixIkcPXqUl19+OdVzatasScOGDfnoo4/Yvn07AwYMSLGIS3Ly5MnD0KFDefzxxwEIDQ116fwbN25w8OBBvLy8qFevnsv3z0i3bt2ic+fObNmyhXHjxvH22287PG7Pnj2YTCZatGhh9xQcLE/Fg4ODiYuL4/Dhw07dt127dsTHx/Pjjz+m+TuIiGfN4xDlYqbRmoWUZybzcD2ZkdxD43nGsq6ddzTNPKF+/fqxf/9+bt68SVRUFBs2bKBSpUocP36c4sWLOyy+5oh1zXh0dHTaAhcRj/PUeK7EO4uaOHEiZcqU4eOPP+bMmTOpHv/EE09w4cIF4uPjU52Wlprknhyn5v333+fmzZt06NAhS1XxvnXrFl26dGHLli08//zzvPvuu8kea60mm7hlmJV1e758+Zy6t/WNgbWCuohkTxGYGHZyIeZqH8Kq34jHzHDW6c23pErjefo7cuQIYWFhVK9enSZNmrh8/sqVK4mJiXE4RT051jfd9957r8v3E5GsIwITw8LmYK40G3adzdTxXIl3FlWgQAHGjx9PbGwsb7zxRqrH9+vXj9WrV/P9999TpUqVFI/duHEj3377LXfv3k2y78SJE6xYsQJIvQKrVUxMDO+99x6TJ0+mcOHCTJkyxW7/zZs3OXbsWIrTs9MquXtYp5dv2bKFMWPGpFrcpnHjxnh5ebFy5cokb7XDw8NZuXIlBQsWpHHjxrbtBw4ccHit8PBw5syZg7e3NyEhIW5+MxHJCn48cxhz64Vw+hpM3gl344nDzAkiPR2aZHEaz13jzD2sRdWsPdKTExUVlWTb0aNHGTt2LD4+Pkn6lCdXwX3WrFmEhoZSuXJlGjZsmNpXEJEsJuG08u8O7cTcbjFERMGUXQCZNp6rqnkW9uSTT/Luu++yaNEiJk6caNejPLHChQvz6KOPOnXdY8eOMXr0aEqUKEFwcDAVK1bEbDZz4sQJNmzYwJ07d3jqqafskkurlStXcuzYMcAyFe306dPs3LmTK1euULZsWb788ktq1Khhd85PP/1Eq1ataNGiBT/88INTMe7atcs2jcz6lnnXrl0MGjQIsEz5Sli0LLl7jBgxgi1bthAQEECRIkVs1WYTGjRokO0JdmBgIOPHj+ftt9+mYcOGdO3alfLly3PmzBnWrFnDnTt3mD17tm1tGECPHj3IkycP9evXp1y5cty5c4fff/+dLVu2YDabmTVrlp6Qi2Rj586d48XW/eGsCe4vDpv6QR4jXhiohJ+nw5NsQON52sdzqzt37vDll1+SN2/eZNusWY0dO5ZDhw7RsGFD/Pz8OH78OOvWrcNoNLJmzRpbpXOr7t274+3tTYMGDQgMDCQ6Opp9+/bxv//9j6JFi/Lll1/i5eXl1PcWkaxhHod4knXEY8bw8yUKtF0C125Ds7KwrAdApo3nSryzsPz58zNhwgSeffZZJk2axKJFi9Llun379qVw4cJs2rSJI0eOsGXLFm7fvk2JEiVo164dgwYNonv37g7PXbVqFatWrcJoNFK4cGFKlSpFy5YteeSRR+jVq1e6tRg5ceIECxcutNt28uRJTp48CVhaezlTLdw6re/ixYt27UMSatmypV1i/NZbb1GrVi0+/fRTNm3axPXr1/H19aVVq1Y899xzdOjQwe78iRMnsn79evbt28e6deuIj4+ndOnSPP7444wcOdLhHzwikj389ddftGrVirOn/6RkxUCubu9FfEBhvDDwKZ0IJOtNw5WsR+N52sdzqzVr1nD16lV69epF8eLFUzy2Xbt2HDt2jBUrVnD9+nUCAgLo27dvsg8/nnrqKTZt2sTOnTu5evUqRqOR8uXLM2rUKMaOHUtgYKDTcYqI50VgsiXd/HoZc8gibkbepFzjB4jY0Jn4wnkzdTw3mM1mc4bfJZuLiorC19cXk8lk96ZTRERyrosXL9KiRQv++OMPKlSowI4dOzCU9eEEkVTCL02DtMaVzKd/cxGR3CWU07RmIRy7Ai0XwKVoaFCGdVs2UKfovZk+nuuNt4iISCKXL1+mdevW/PHHH5QrV47t27fbpqXqLbeIiEjWE4GJ40RS+d9kujJ+GI5HWmq0XIqGOgEYN/WjTtF7CcQ308dzJd4iIiIJXLlyhZCQEI4ePco999zD9u3bVadBREQkC0u4ltuIgbl0ouVJX4q2WsY/F25AzVIYt/Rnrl9vjz1AV+ItIiLyr8jISNq2bcuRI0coXbo0oaGhKRbCEhEREc+yW8sNxGPmyTOLKN16Ff/8dZn7H6jKO1sX0bDE/R6dtabEW0REBLh27Rrt2rUjPDycUqVKsX37dipXruzpsERERCQFx4m0Jd0AnDMR33ohf529xv3338+ObaEElArwXID/Uh9vERHJ9aKionjooYc4ePAgJUqUYPv27VStWtXTYYmIiEgqKuOHEYPlw19R0HoRnL5G+YoV2L59OwEBnk+6QYm3iIjkcjdu3ODhhx9m//79+Pn5sXXrVqpXr+7psERERMQJgfgyl04YL96wJN0nIilR4R5+DN3BPffc4+nwbJR4i4hIrhUdHc0jjzzC7t27KVq0KFu2bKF27dqeDktERERc0OlyIJXafAd/XOWecoGEbd9l60aSVSjxFhGRXOnWrVt07tyZnTt34uPjw+bNm6lXr56nwxIREREXHL5yiqCQYP747Rj33HMPO7b/kCW7kai4moiI5Dq3b9/m0UcfZfv27RQuXJiNGzfSsGFDT4clIiIiqUjYr3tV5CFGtX0cjlyE0oV5OvTDLNuNRIm3iIjkKjExMXTv3p3NmzdTsGBBNmzYQFBQkKfDEhERkQTCiOBHztKccjQkELDv182129BuEYRfhFKFYPtAXq38MwNo5dG2YclR4i0iIrlGbGwsvXv3ZsOGDRQoUIDvvvuO5s2bezosERERSWAQq1nIz7bPA6nNMzT8L+mOioGHvoSDF6BEQdg+AKqWIA4zJ4hU4i0iIuIpsbGxPPbYY3z77bfky5ePtWvX0rJlS0+HJSIiIgmEEWGXdAMs5Of/tt24Aw9/Bfv/Ar8CsLU/VC8FgBcGKuGX2SE7RcXVREQkx7t79y4DBgxg1apV5M2blzVr1hASEuLpsERERCSRHzmb/M7oO/DIEth9Dormhy39obalT7cXBj6lU5Z82w164y0iIjlcXFwcgwcPZunSpXh7e7Nq1SoeeughT4clIiIiDjSnnOMdt2Kh81LY+Sf45IPN/aBeabww8DXdCaJslk26QW+8RUQkB4uPj2fo0KF8+eWX5MmTh+XLl9OxY0dPhyUiIiLJaEggPahmv/H2XXh0GWw/DYXzwsa+0PAe21vuntTI0kk36I23iIjkUPHx8YwYMYIFCxbg5eXFkiVLePTRRz0dloiIiKRgHof4hmP/bYi5C92Xw+aTUNAb44a+vBv0BA0oQyX8snzCbaXEW0REchyz2cyzzz7LZ599htFoZPHixfTs2dPTYYmIiEgKIjD9V7kcIDYOeq+EDcehQB6e+W4GLzbvl22S7YSUeIuISI5iNpsZPXo0H3/8MQaDgfnz5/PYY495OiwRERFJRgQmjhPJ30TbJ92PrYJvf4d8XhjXPsaLLbNn0g1KvEVEJAcxm82MGzeOWbNmAfD5558zYMAAD0clIiIiVtYku/K/08Tnccj+LTfA3XgYsAZWHYW8XhjW9GFuyKhsm3SDEm8REckhzGYzL7/8MtOmTQNgzpw5PPHEEx6OSkRERKwSJtkGYCSN+Igw+6Q7Lh4GfwtLfwFvIx1WTWTuQ2OzddINSrxFRCSHmDx5Mm+//TYAH3zwAcOHD/dwRCIiImKVeP22GfiAn+wPijfDsHXw5WHIY4TlPRnXcXC2T7pB7cRERCQHePvtt3n99dcBmD59OiNHjvRsQCIiImLnOJH2b7YTizfDU+thfjh4GWBJN7werUYl/DItxoykxFtERLK1qVOn8tJLLwHw7rvvMnr0aA9HJCIiIolVTimBNpvh2Q0w9xAYDbCoK149a/ApnXLE227QVHMREcnGZs6cybhx4wB44403bL+LiIhI1hKIL32pyVccsd9hNsPoTfDxATCAYX4Xlj0+iSDK5pikG/TGW0REsqmPPvrI9nb71Vdf5eWXX/ZwRCIiIpKSOgTYbzCbYfxWmLXf8vnzzpgH1OYnzidJuiMwEcppIjBlUrTpS2+8RUQk25k7d65tHfeECRNs67tFRETEcxK3Cku4rTDejGfrfwebzfDydpi6x/J5ziPwRF0AprOH52hsu0bCauhGDMylE0Ool6nfLa30xltERLIsR0+3v/jiC1vF8rFjx/LWW29hMBg8FaI4YefOnXTq1IkyZcpgMBhYs2aN3X6z2cyrr75K6dKlKVCgACEhIRw/ftzumMjISPr27YuPjw9FixZlyJAh3LhxIxO/hYiIpGQehyjPTFqzkHLM4AU2M5Xdtm2N+dy+uNrkHfD2LsvvH3SA4Q1su+KBE0QCSauhx2NmOOuy3ZtvJd4iIpIlJRzAyzOTeRxi8eLFDB06FIDnnnuOqVOnKunOBqKjo6lduzYfffSRw/3vvfces2fPZs6cOezfv59ChQrRvn17bt++bTumb9++/Prrr2zZsoX169ezc+dOnnzyycz6CiIikgJHrcKmsYdxbLHbZvP2j/D6Dsvv09vByEZ21/PCYKtm7qgaehxmW2KeXWiquYiIZDmOnm4P+/ptDINWYzab6fxUX8bOeF1JdzbRoUMHOnTo4HCf2Wxm5syZvPzyy3Tp0gWARYsW4e/vz5o1a+jTpw9Hjx5l48aNhIWF0aCB5Y3IBx98wMMPP8y0adMoU6ZMpn0XERFJKtVWYQlN3Q0vbbf8/m4IjA6y220Au2rmlfHDiMHu+gkT8+xCb7xFRCTLSTKAr/wNc/9viI+Ph6H1WPthRe41zGIehzwXpKSL06dPc/HiRUJCQmzbfH19ady4MXv37gVg7969FC1a1JZ0A4SEhGA0Gtm/f7/D68bExBAVFWX3IyIiGcOaHKdq5j4Y9+867zdawbhmdrsNwH6G2q3fDsSXuXTC69/re2HIlm3GlHiLiEiWUxm//4bvb4/BY6sgzgyD6sCnHcFoyLZrvMTexYsXAfD397fb7u/vb9t38eJFSpUqZbc/T548+Pn52Y5JbMqUKfj6+tp+ypYtmwHRi4iItXhaN6qlfOBHP1nahgG8GgwvByc55DM605DAJNuHUI8zjCKUgZxhVLYrrAY5LPF+5513MBgMjBo1yrbt9u3bPPPMMxQvXpzChQvTvXt3Ll265LkgRUTEeev/gJ4r4G489K0Jn3cC439P1LPjGi/JHBMmTMBkMtl+zp075+mQRERynKnspiwzaM1CVvKbw2MeoTI9596Ckd9bNkx4EF5vmeS40TROMaEOxJeWVMh2b7qtckziHRYWxqeffkqtWrXsto8ePZp169axYsUKduzYwfnz5+nWrZuHohQRkdREYGI5v2LedAK6L4fYeOhdHRY8itHLy+7Y7LjGS+wFBFh6uiZ+KH7p0iXbvoCAAC5fvmy3/+7du0RGRtqOSSxfvnz4+PjY/YiISPqZxm7GsSXV4777Yjkrhr9n+TA2CN5qDQ5qtNxP8fQOMUvJEYn3jRs36Nu3L5999hnFihWzbTeZTMybN4/p06fTunVr6tevz/z589mzZw/79u3zYMQiIpJYBCZeYDPlmMHYbXPg0WVwJw66V4PFXfHK48W7hGT7NV5ir0KFCgQEBLBt2zbbtqioKPbv309QkKXgTlBQENeuXePgwYO2Y7Zv3058fDyNGzfO9JhFRLIzR6063bmGM0k3i3+GoWstvz/XGKa2dZh0A3SkitvxZAc5oqr5M888wyOPPEJISAhvvvmmbfvBgweJjY21K9hStWpVypUrx969e2nSpInD68XExBATE2P7rIIsIiIZax6H/qti/sMZ6PQ13L4LnavAku54eefhUzoxhHr0oQYniKQSfkq6s4kbN25w4sQJ2+fTp08THh6On58f5cqVY9SoUbz55ptUrlyZChUq8Morr1CmTBkeffRRAKpVq8ZDDz3EsGHDmDNnDrGxsYwcOZI+ffqoormIiAsSjrdGDMz9d2xNjXUdd+V/x97jRKZew/zrIzDoW0sfsacawIz2YDBgxMCLPMgUfsSMpaDaZ3TO8WN6tk+8ly5dyqFDhwgLC0uy7+LFi+TNm5eiRYvabU9YsMWRKVOmMGnSpPQOVUQkx0s8MKd2DMAezv2XdO86Cx2XwK278HBlWN6Dp/M2YRC1bcVWAvHN8YNzTnPgwAFatWpl+zxmzBgABg4cyIIFCxg3bhzR0dE8+eSTXLt2jQcffJCNGzeSP39+2zlfffUVI0eOpE2bNhiNRrp3787s2bMz/buIiGRXjlp1Dmcd7amY4rjqKFn3Sq2C+crfoP9qiDfD0Lrw4cO2N93xmGnLfTxFg1z1ID1bJ97nzp3jueeeY8uWLXaDc1pNmDDB9kcBWN54qxqqiEjKnHmKnvAY65Bte2K+LwI6fAXRsdD2PljVC/Ll4WPCmMMBp5/KS9bTsmVLzObk340YDAYmT57M5MmTkz3Gz8+PJUuWZER4IiK5gqNe29YipSk9LE+crA9jbcpvu5N0I7EvjGqtz5LbHqRn6zXeBw8e5PLly9SrV488efKQJ08eduzYwezZs8mTJw/+/v7cuXOHa9eu2Z2XsGCLIyrIIiLimuSeoidcP5b4GDMJku4D56H9l3DjDrS6F9b0gfz/PRtW6zAREZG0cdRrO7UipY6S9RST7u9S7kYC0I9auSrhtsrWiXebNm04cuQI4eHhtp8GDRrQt29f2+/e3t52BVt+//13zp49ayvYIiIiaZfSU/SUjgHgfxeg7WKIioHg8rDuMSjoneQwtQ4TERFxXyC+dtPEnSlS6ihZT9amE9DNvhtJDS//JGd/yeFc+SA9W081L1KkCDVq1LDbVqhQIYoXL27bPmTIEMaMGYOfnx8+Pj48++yzBAUFJVtYTUREXGcdmBMm1omfojs6hsOXIGQxXLsNTcvC+segUF6H91DrMBERkbQZQj3aU9HptdXWZH0464hL6V33tlP/dSPpZulGQh4jv/J3krNSm96eU2XrN97OmDFjBh07dqR79+4EBwcTEBDAN9984+mwRERyFGefog9LuEb718vQZhFE3oJG98D3faFIPofXV+swERGR9BGILy2p4PSYOoR6TCEk+QN2nPmvG0mn++Hr7uDtBTielp5bH6QbzClVOxHAUlzN19cXk8mk9d4iIimIwOTwKbpduzCAY1eg5QK4FA31S8PWAVDUvkimEQPvEEJDyuS4iqcaVzKf/s1FRNwTgYlyzHD8vnvXWXjoS0th1IcrwzeWwqiJWWe8WR+k55Riqa6MLdl6qrmIiGQtjiqUJi6qxvGr0HqhJemu7Q+b+ydJug3APobYWoiJiIiIZ/RgueOkO5luJIl5YWAvQ4gmNsc9SHeFEm8REclQdkXVTv0DrRfBhRtQo5TlTbdfgSTnvEdbJd0iIiIeFIGJF9nKfv5KujOFbiSWYmxm4rEk3aMJojRFcm3CbZXj13iLiIhn2Sqi/nkNWi2EiCioVgK2DYASBZMc/xLNeZ5mmR+oiIiIEIGJF9hMWWbwFUeSHpBKN5J4zCylB8/TlHjMTGMP5ZnJPA5l4rfIepR4i4hIhonAxB7O8di5spak+6wJ7i9uSbpLFUpy/HDq8yZtPBCpiIiIzOMQ5ZnJNPY4PsCJbiReGLiXokxnr22KejxmhrMuV7YRs9JUcxERyRDzOMQw1mI+fx1aL4DT16BiMdg+AEoXSXK8FwZeJjjT4xQRERHLw/JhrE2+aZgT3UisxdNuEGvfPpTc20bMSom3iIiku/X8zlDWwsUblkJqJyLh3qKwfSDck7Tqp9qFiYiIeNYs9iefdB+7Ykm6r9y0dCPZ1A98krYA/Zru9KQGEZhslcytcmsbMSsl3iIikmYRmDhOJJXx42W2s5Cf4XK0ZZD+/SqU9YHQgVAuaWI9g/b04AEl3SIiIpnIOnYXxpvTXEt+erkT3UjAklgHURawdDmZSyeGs464BG3EcvNYr8RbRETSJGGPbtvT7as3IWQR/PY33FPEknTfWzTJuV4YlHSLiIhksoRjd4qc7EZihCSJ9RDq0Z6KnCAyV7cRs1LiLSIibkvcozseM/xzy1Lt9MhlKF3YMr28YtKpZUYMvENIrh+IM0poaCjbtm1j9+7dREREcOXKFQoWLEjJkiWpWbMmLVq0oGPHjgQEBHg6VBERyUSJx+5kOdGNxAiMoSnP0djheB6Ir8b5fynxFhERt9n16AZLldN2X8L/Llqqlm8bYKli/i8jBrpRjVX8RjxmxrOVYhRgCPU8EH3OEx0dzezZs/nss8/4888/MZst/7fJnz8/fn5+3Lp1i19++YXDhw/z1Vdf4e3tTadOnRg9ejTNmqmFm4hIbpBk7HbknCnVbiS9qc402imxdpLaiYmIiNtsPbrB0s+zw1dw4Lzlifi2AVCtpO1YI/AtffiGo2ovkgHmzJlDpUqVeOmll/Dx8eGNN95g27ZtmEwmbt68SUREBFevXiU2NpZjx46xcOFCevXqxebNmwkODqZbt26cPn3a019DREQymN3Y7cj565bp5al0I2lB+YwLMgdKl8TbZDIRGxubHpcSEZFsIIwIprOHcC7yGDXgxh14+CvYFwHF8sPW/pa1YP/ywsBcOlOIvMm2F5G0efbZZ2nbti2HDx8mPDyciRMn0qpVK4oUsf9jyWAwcP/999O/f38WL17MpUuX+PTTT/n5559ZvHixh6IXEZGMEIGJUE7bHnBbC6r1oJrjE5zsRgLwNBsoz0zmcSiDos9ZXJ5qfuPGDVasWGFbN3b+/Hnu3r0LQJEiRahZsyYtW7akS5cuNGjQIN0DFhERzxrEakvVcqubsdBxCew+B775YEt/qP3fuuGEVcsjMGEAu9Q7t7cXSS+//vor999/v8vnFShQgKFDhzJ48GDOnj2bAZGJiEhGSNhRxNF074QF1AxAdx7gG44mP838b+e6kSRknbnWnoqacp4KpxPvc+fO8eabb/L1119z48YNAIoVK0bFihVt68YiIyPZt28fu3fv5u2336ZOnTqMGTOGvn37ZtgXEBGRjGcd3KO5Y59034qFzl/Djj8t/Tw394f6ZWy7E1ct38RJu+saSFoFVdzjTtKdkJeXFxUqVEinaEREJCMl7igyl0529VISF1AzAyv5LfkLXr0JIYtT7UbiiHXmmsbylDmVeL/44ovMnj2buLg4OnToQK9evQgKCnI4QN+8eZODBw+yefNmlixZQv/+/ZkxYwafffYZdevWTfcvICIiGWsquxnPlqTPx2/fha7LYNtpKJwXvu8Lje6x7U6cVFv/CEh4HSMG2lMxo7+CiIhIjuGoo8hw1lGLUpzmmu24VAuoWVm7kRy+BAHJdyMxAG/RmpfYrplrbnAq8Z4zZw7PP/88o0aNws8v5X/UggUL0rx5c5o3b84bb7zB1q1bmTx5MuvWrVPiLSKSzUxjN+PYknTHnTjosRw2nYSC3rDhcWha1u4QQ6Kk2lEVVT0lz3zHjx8nPDzc9vPzzz8TERHh6bBERMRJyY2njfnc2VT7P6ZE3Ui223cjSegzOjOEepSiMMNZRxxmvDBo5pqTnEq8T58+TbFixdy6QUhICCEhIfzzzz9unS8iIp4RgYnxbE26IzYOeq+E745DgTyw/jFonrSyaXyipNpaRTXhHwt6Sp42Bw8e5NVXX+XkyZM0aNCAqVOnUrp0aQBiYmJshdasP0eOHCE6OhrA1mrMYEihsq2IiGQ5jsZTwPWkOyoGHkq+G0lCn/CwbSr7EOrRnoqcIJJKyawvl6ScSrzdTbrT+xoiIpJ5HPb5vBsPj38Da45BPi/4tg+0crwuOHFSHYgvc+mkp+Tp5NSpU7Rq1YoWLVrw1ltvMX/+fNq0aUPdunUJDw/n+PHjxMXFAdj18zabzVSvXp0hQ4ZQvXp1atSo4cmvISIiLko8nhqBeFcvkko3koQMQEeqJIlB47drXK5qLiIiucNqjtpviIuH/qth5W+Q1wtW94a2ya/P7ka1JIOynpKnn/Xr1xMdHc2XX36Jr68vbdq0wc/Pj99//x2j0UilSpWoUaMGNWrUoGbNmtSoUYOKFSvi7e1NUFAQo0aN8vRXEBERNyUcT7dyirf40fmTU+lGkthYmmq8TgdOJd47d+50+wbBwcFunysiIp4RRgQf8NN/G+LiYfC3sPQX8DbCyp7QoXKK11jBb0xlNy/QzG67npKnjzJlymA2m9mzZw8dOnRgz549gGXq+HPPPcekSZMoVKiQh6MUEZH05KiFWBsWOX+BVLqRONKLB9ISsvzLqcS7ZcuWbq8Bs05zExGR7GFq4oJq8WYYtg4WHwYvAyzrAZ2qJH+BBF5kC49RQ4l2BujevTudO3emU6dOlC9fHrPZzHvvvcf777/PjBkzWLJkCZMnT2bIkCFaxy0ikgM4aiF2jCvOVy9PpRtJcqKJTWPkAk4m3q+++qoGbRGRHC4CE2+yk085+N9GsxmeWg/zw8FogCXdoWs1p68ZD6pankEMBgNr1qwhLCyMS5cu0bx5c3x9fRkxYgRvvfUWM2fOZPjw4cyePZtp06bRrl07T4csIiJuSq6FWJyzSbcT3UgcURHU9ONU4v36669ncBgiIuJJ09jNC4nbhpnN8Oz3MPeQJele3BV6VXfpuhqwM17Dhg3tPhcuXJgpU6YwYsQIxo0bx4oVK+jQoQPt2rVj6tSpHopSRETSIrkWYk5xshtJYiqCmr6Mng5AREQ8a2pySfeYTfBRmKWc6Red4fGaqV7rYSrZBhYN2J5Vvnx5li1bxq5du2jQoAGbNm2ibt26msEmIpKNRGBiOb9wjL8xYv/fby+c+O+5C91IwJIcvkdbQhnIGUbZWohJ2qW5qvnu3bsJDw8nKioKHx8f6tSpQ7NmzVI/UUREPC6MCPv13GBJusdvhZn7LZ8/6wQD66R4HSMG3iWE52lGBCZVLc9CmjZtyv79+/nqq6+YMGECERERLF26lMqVKzN69Gjy5FGDExGRrGgehxjGWrv32tb+3V4YqEMAB7mQ/AVc7EYCsI+hNCQwfb6A2DGYrc09XbRnzx4GDx7MiRMnAEuPUOtT9MqVKzN//nyCgoLSL1IPioqKwtfXF5PJhI+Pj6fDERFJF0mKqIEl6X4lFN76ty3JJ4/AiAaA5cX3cOozl0O2wi4TeJDa+GMGmlJWibaTPDWu3L59m6lTpzJ16lSio6OpUqUKs2bNom3btpkWg6doLBeR7CQCE+WZmWR6uQFYRg+iiWUw3yZ/AWs3ksWHIY8RvunlVGHU5fSgJzXSGH3u4crY4lbi/euvv9K4cWNu3rxJ27ZtadWqFaVLl+bixYuEhoayefNmChcuzL59+3jggexffl6DtYjkNA7XdANM3gGv/WD5ffZD8Gxju92hDKQSfrY32ps4maTCqqalpc7T48rFixeZOHEiixZZWtDcvXs302PIbJ7+NxcRcUUop2nNQof7elGd5fya/MnxZhi2Fr4It3QjWd4TujlXGNUAfEZnjeVOcmVscWuN9+TJk7lz5w4bNmxg06ZNvPjiiwwcOJDx48ezceNGNmzYwO3bt5k8ebJbX0BERDJOBCbHSfeUH/9Lut9vlyTpBjjAeQLxpSWW9WGOKqxGYMqo0CUVH3/8MX/99VeqxwUEBPDFF18QFhZGcHBwJkQmIiKuqIxfkjXdVikm3WYzPP2dJem2diNxMukGMIPG8gziVuL9ww8/0KNHDx566CGH+x966CF69OhBaGhomoITEZH09398n3TjtD0wcbvl93fawBjHS4VeZKttME6uwuoJItM1XnHeyJEjKVeuHA0bNuStt97iyJEjKR5ft25dtm/fnknRiYiIswLxZS6dkk2+HbJ2I/n0oOXVdSrdSAzAKJI+ZNdYnjHcSrxNJhMVKiRfDQ+gQoUKmEx6UiIikpX0ZDmrOWa/cdY+eOHfN+CTW8L4B5M9P+Fg7OhpvNqHeVZYWBgTJ07kzp07vPLKK9SpU4eKFSsyduxYduzYQXx8vKdDFBERJw2hHn8yik94mCapFTxL3I1kfpdUu5F8RmfG0lRjeSZxK/EuU6YM+/btS/GY/fv3U6ZMGbeCEhGR9BWBiU/4iZX8Zr/j4zAYtcny+yvB8EqLFK+TeDAeQ5CtnYnah3le/fr1eeONN/j55585deoU06ZNo1y5csyePZvWrVvj7+/P4MGDWbNmDTdv3vR0uCIikoqv+YWn2cA+IpI/yGyGF13rRvI2rRlCPdubdY3lGc+txLtz58788MMPvPLKK9y+fdtu3+3bt3nttdcIDQ2lS5cu6RKkiIi4LgIToZxmGrspxwyeZoP9AXMPwjP/bnuxGUxqmeo1pxBCIL7M4xDlmck09hCPmedpqn6fWcy9997L6NGjCQ0N5dKlS8yfP5/mzZuzcuVKunXrRokSJejUqRNffPEFly9f9nS4IiKSyLR/u4+kWAnb2o3kvT2Wz588AkNSH4v7U9v2+xDqcYZR6t2dwdyqan716lUaN27M6dOnKV68OI0aNcLf359Lly4RFhbG33//zX333cdPP/2En1/2n6agSqgikt3M45Bd4bMk5v8Pnlhr+X1ME5jWDgypryOzVjVP3OLECwNnGKUn5E7y5LgSExPDli1b+Pbbb1m/fj2XLl3CaDTSpEkTdu3alamxZCaN5SKSnURgoiwzUj8wlW4kjnyuquXpxpWxJY87NyhevDj79u1j3LhxLF26lA0b/nuLkj9/fgYPHsy7776bI5JuEZHsJgJTykn3l4dhyL9J9/81cjrptk4zT6momhLvrC9fvnx07NiRjh07Yjab2bt3L99++y1r1671dGgiItlSBCaOE0ll/NI8DlqvtZezqR/sRDeSxNSn23PcSrwBSpQowRdffMGnn37KsWPHiIqKwsfHh6pVq+Lt7Z2eMYqIiBOsg/XfRCefdC/9BQausfQLeaoBzHzIqaQbIIT7bH9QGDEkeeOtQizZj8FgoGnTpjRt2pR3333X0+GIiGQ7CWeYGTEwl05uv02eym7Gpza13MrJbiQJGYEgyroVm6Sd24m3lbe3NzVrplwxT0REMlbigd+hVb9Bv28g3gxD68KHDzuddANs4SQRmGyFWIazjjjMKsSSRTzxxBNunWcwGJg3b146RyMikvMlnmEWj5nhrKM9FVMcExO+Ib/AdX7kLL9wmfmEO3djF7qRWBmAuXTWWO1BaU68RUTEsxwN/Aawf2L+7THoswrizDCwNnzaCYwu9AYF4sE2nXwI9WhPRU4QSaV0mFonabdgwQK3zlPiLSLiHneWXqVagyU1LnYjeY1gqlOKIMpqrPYwtxPvXbt2MW3aNH7++WfOnz/P3bt3kxxjMBgcbhcRkfTjaOC3+/TdH9BzBdyNt/T0nNfZ5aQbkk4nD8RXg3gWcvr0aU+HICKSq1TGz6WlV6nWYEmNi91IjMBQ6musziLcSrwXL17MoEGDMJvN3HfffTRq1Ig8efTyXEQks0VgSrkAy6YT0G05xMZDr+qw8FHwcr2TpKaTZ33ly5f3dAgiIrmKq0uvHD0od9r8/8Hw9ZbfxzSBt9ukuFxMU8uzHrey5TfeeINixYqxYcMGGjVqlN4xiYiIE1KdrrbtFDy6DO7EQdeq8GVXyJM06U4yLT2B4dSnDzU0nVxERMQBV5ZeOXpD7pSE3UieTbkbiQH4mIfpSBWN21mM6689gHPnztGnTx8l3SIiHpLqdLUdZ6DT13D7LnS6H5b2AG+vJIcZgB484PASRuBlgmlJBQ3e2dju3bsZNmwYDRs2pEqVKjRs2JAnn3wyR/fsFhHJTIH4OjVWBuJLf2q5dvGE3UhG1IdZKXcjMQNVKalxOwtyK/EuX748d+7cSe9YXPbJJ59Qq1YtfHx88PHxISgoiO+//962//bt2zzzzDMUL16cwoUL0717dy5duuTBiEVE0keK09V2n4VHlsCtu9ChEqzoCXmTJt1gGaC/4ajDfe/QVgN3Njd69GiCg4OZN28eBw8e5MSJExw8eJDPP/+cFi1aMGbMGE+HKCKSK0RgYjm/sJCfnT8pcTeSjx5JtRuJ2ntmXW4l3sOGDWP9+vVERkamdzwuCQwM5J133uHgwYMcOHCA1q1b06VLF3799VfA8gfHunXrWLFiBTt27OD8+fN069bNozGLiKSHaJJ5+LkvAjp8BdGx0PY++KY35Et5VVFcMgl8Q8qkNUzxoIULFzJr1iwqV67MV199ZSuEeuHCBZYsWcL999/PrFmzWLRokadDFRHJcSIwEcppIjAxj0OUZya9Wen8BdzoRqJ6LFmbwWw2u7XC/5lnnmH79u28/PLL1K5dGx8fH4fHlStXLk0BusrPz4+pU6fSo0cPSpYsyZIlS+jRowcAx44do1q1auzdu5cmTZo4fc2oqCh8fX0xmUzJfk8Rkcwyjd28wJakOw6ch5BFYIqBVvfC+sehoHeq13O0xtsLA2cYpcE7g2TGuNKkSRPOnz/PkSNH8PVN+n9Hk8lEzZo1KVOmDPv27cuQGLISjeUiklmmsZvxbLW194Tka6k4tOE4PLrUUhj18Zqw6NFUC6MagP0MpSGB7gUtbnFlbHG7FHm9evVYsmQJAwYMSPaYzGwnFhcXx4oVK4iOjiYoKIiDBw8SGxtLSEiI7ZiqVatSrly5VBPvmJgYYmJibJ+joqIyNHYREWdEYOJNdvIpB5Pu/N8FaLfYknQ3LwfrHnMq6QbHfwy8Q4iS7mzu119/ZejQoQ6TbgBfX1+6d+/O559/nsmRiYjkXFPZzbgED8ddfsO5+SR0W+ZyNxIzEE2sq3eTTORW4v3BBx8watQovL29adWqFaVLl/ZYO7EjR44QFBTE7du3KVy4MKtXr+aBBx4gPDycvHnzUrRoUbvj/f39uXjxYorXnDJlCpMmTcrAqEVEXJNiBfMjl6DtYvjnNgQFwnePQ6G8qV7TCAyjvsNEvoGmmecKhlTWCoqIiPMiMDHe0Yw0Z207BV2WQkzK3Ugc0drurM+tbHnGjBncc8897Nmzh8BAz05nqFKlCuHh4ZhMJlauXMnAgQPZsWNHmq45YcIEu4IzUVFRlC1bNq2hioi4JcUK5r/9DW0WwdVb0Oge+L4vFMmX4vWMwFJ6EITlv2ufccju2hq8c4bq1auzatUq3njjDQoXLpxk//Xr11m1ahXVq1f3QHQiIjnPcSLd7dLtdDcSR4ygtd3ZgFvF1S5evEj37t09nnQD5M2bl0qVKlG/fn2mTJlC7dq1mTVrFgEBAdy5c4dr167ZHX/p0iUCAgJSvGa+fPlsldKtPyIinpJsBfPfr0DrhfD3TahXGjb1A9/8KV7LCwNz6UxPahCIL4H4MpdOeP27Ck2FWXKO4cOHExERQVBQEKtWreLKlSsAXLlyhZUrV9K0aVMiIiJ46qmnPBypiEjOUBk/3JpH5EI3ksSGU58/Gc0Q6rlzZ8lEbr3xrlSpUpKENquIj48nJiaG+vXr4+3tzbZt2+jevTsAv//+O2fPniUoKMjDUYqIOCcCE8f4O+mOE5HQehFcioba/rClPxRNOekG2MuQJIVXhlCP9lTkBJFUwk9Jdw4xePBg/ve///Hhhx/Sq1cvAIxGI/Hx8QCYzWaeffZZBg4c6MkwRURyjEB8GUtTprHH+ZPc6EaSUJ9/H6RL1udW4j169GjGjh3Ln3/+Sfny5dM7JqdNmDCBDh06UK5cOa5fv86SJUv44Ycf2LRpE76+vgwZMoQxY8bg5+eHj48Pzz77LEFBQS5VNBcR8ZR5HGIoa5PuOP0PtFoI569D9ZKWpNuvgFPXTK7wivXtt+Qss2fPpmfPnixYsIDw8HCioqLw8fGhbt26DBw4kObNm3s6RBGRHKUF5Z1PvA+ch4e+hOt3LN1I1vSB/M6nZ1oalr24lXhXrFiRFi1a0KBBA0aNGpViO7Hg4OA0BZiSy5cvM2DAAC5cuICvry+1atVi06ZNtG3bFrCsRTcajXTv3p2YmBjat2/Pxx9/nGHxiIiklwhMDHOUdP95zZJ0R0RB1RKwbQCULOTUNY0aoHOl5s2bZ/kE+/XXX09S1LRKlSocO3YMgNu3bzN27FiWLl1qN577+/t7IlwRETsRmDhOJAc5b1fRPEVudiOxtgDV0rDsx60+3kajEYPBgPXUlKqixsXFuR9dFqHenyKS2ZbzC71Zab8xIgpaLIBT/0BlP9gxCEoXcfqaI6jPJ3RKst36B0NlTTPPNBpX7L3++uusXLmSrVu32rblyZOHEiVKAPDUU0/x3XffsWDBAnx9fRk5ciRGo5Hdu3c7fQ/9m4tIRpjKbsazxbWiakcuWR6iX71l6UayqV+qhVGHU5+XsbzQ1NKwrCPD+3i/+uqrakEiIpJBIjCxh3P2G89ftxRSO/UP3FcMtg90KekGOMqVJNsStikzYmAunVSgJYeJi4sjIiKC8+fPExvreKlBRs5Oc1aePHkcFj81mUzMmzePJUuW0Lp1awDmz59PtWrV2Ldvn5aPiYjHTEvUs9spbnQjmUpbnqeZ7bMS7uzJrcT79ddfT+cwREQkAhOz2J90bdilG5ZB+ngk3FsUQgdCoOtv7HbwJ2FE2IqrJW5TFo+Z4ayjPRU1qOcA8fHxvP3228yaNYvIyMgUj80Ks9OOHz9OmTJlyJ8/P0FBQUyZMoVy5cpx8OBBYmNjCQkJsR1btWpVypUrx969e5NNvGNiYoiJibF9joqKyvDvICK5RwQmXnA16XajG4kRSwE1yf6cTrzHjRtH165dVRFcRCQDJHzzbOfvaEv18mNXoKwPbB8A5dxPindzzpZ4O2pTFoeZE0Qq8c4BJkyYwNSpUylVqhSDBw+mdOnS5Mnj1vP2DNe4cWMWLFhAlSpVuHDhApMmTaJ58+b88ssvXLx4kbx581K0aFG7c/z9/bl48WKy15wyZUqSdeMiIunFYfHTlLjZjSQeNC7nEE6PwNOnT+f999+nZMmSdOrUiS5dutC2bVvy5Ut5aoSIiKQsjAiGsTbp+rCrNyFksWVaWpkilunlFYo5dc1W3EsoZ5Jsb0ZZ2++V8cOIwS75VoXUnGPhwoVUqVKFsLAwChcu7OlwUtShQwfb77Vq1aJx48aUL1+e5cuXU6CAcxX7E5swYQJjxoyxfY6KiqJs2bIpnCEiuZE7dU7CiGATJ52/SRq6kWhczjmMzh544cIF5s6dS6NGjViyZAldunShRIkSdO/enUWLFnH16tWMjFNEJEeaxm4a83nSpPufW9B2MRy+BAGFLW+6Kzk/8O7gDD15wG7bQGrb9fAOxJe5dMILS80OVUjNWW7cuMEjjzyS5ZNuR4oWLcr999/PiRMnCAgI4M6dO1y7ds3umEuXLjlcE26VL18+fHx87H5ERBKaxyHKM5PWLKQ8M5nHIafOW8cfzt8kDd1INC7nLE4n3iVLlmTIkCGsXbuWK1eusHLlSrp3787OnTsZNGgQpUuXpmXLlsycOZNTp05lZMwiIjnCVHbzgqNKqKbb0P5L+N9FKFnQMkhXKeHSteOB8hS129ac8kmOG0I9zjCKUAZyhlEqrJaD1KpVi/Pnz3s6DLfcuHGDkydPUrp0aerXr4+3tzfbtm2z7f/99985e/aslr+JiNuSq3MSgSnF8+ZxiDfY6eRNoizTy/80WbqRbB8A/qk/DB1MHY3LOZBb7cQSio+PZ9euXaxZs4a1a9dy6tQpDAYDDzzwAF27dqVz5840aNAgveL1CLUgEZH0ZK1anqRdGMD1GGj3JeyLgOIF4IdBUKNUutzXCwNnGKUn51lAZowr3333HT179mTXrl3Uq5e1/3B7/vnn6dSpE+XLl+f8+fO89tprhIeH89tvv1GyZEmeeuopNmzYwIIFC/Dx8eHZZ58FYM+ePalc+T8ay0UkoVBO05qFDrYPpCUVHJ4TgYlyzHCuddj569BygaUw6n3FLC1AnSyM+hrBvE5rp44Vz8rwdmIJGY1GgoODCQ4OZvr06fz666+sWbOGb7/9lrfeeou33nqLMmXKcO7cudQvJiKSwyVbRA3gxh14eIkl6S6WH7YOSLekG1Q4Lbd55JFHWLBgAR06dKBz587Url072T8KBgwYkMnR2YuIiOCxxx7j6tWrlCxZkgcffJB9+/ZRsmRJAGbMmIHRaKR79+7ExMTQvn17Pv74Y4/GLCLZm6t1TiIwMZZNziXdaexGMomdlKWo3nbnMGl+452S8+fP8+2337J27Vq+//77jLpNhtNTchFJK+tb7sdY5TjpvhkLjyyBH86Abz7L9PL6ZdI1Br3xzjoyY1yJiYlh6NChLFmyBOtQbzAY7I4xm80YDIYs0U4so2ksF5HE5nGI4awjDrNtPbU12U1YdG0TJ52vYv53tGVN969/W7qR7BjkdGHUhDRmZw+Z+sY7JWXKlOGpp57iqaeeysjbiIhkaSm+5Qa4FQtdllqS7iJ5LX090yHpNmIAzMSjAi250ZgxY/jqq6+oVasWPXr0yNLtxEREPGEI9WhPRU4QSaUEVc1THbeTY+1G8qvr3UgS0yy1nMepEXjnTicLCDgQHBzs9rkiItldBCbHrcKsbt+Fbsth6yko5A0b+0HjwOSOTpGjRNvRHxSSO6xYsYL69euzd+9eJdwiIskIxNdufExcdM1paehGYp2LlPCOaiOW8zg1Erds2TLJ9DRn5YbpayIiCVmnlQNs53TyQ/edOOi5AjaegILesKEvNHWtz7Al1U450VbCnTvdvn2bVq1aKekWEXHBcSJdT7rT0I3EAHxGZ4Ak0941fucsTo3Gr776qtuJt4hIbjKPQym/4baKjYM+K2H9H5A/D6x7DIKTtvtKTifu5xWCKU0RJdriUP369Tlx4oSnwxARyVYK4+3aCddjoMNXEHbe0o1k+0B4oKTTpy+jBz2pAaBZajmcU4n366+/nsFhiIhkTwmLrwA8ybrUk+678dD3G1h9DPJ5wbd9oLXj1iWJWd9wf8dxulCVhgRqcBaH3n77bdq0acP69evp2LGjp8MREcny5nHI+SJq8F83kr3udSPxwkAQ/810SzztXXIWzT8TEXFTwuIrRgyMISj16Wlx8TBgNaz4DfJ6wTe9oV1Fp+9pvXo8ZoazjvZU1CAtDm3ZsoWWLVvSpUsXWrdunWw7MYPBwCuvvOKBCEVEsgbrEjGXku6bsdDpa9h11tKNZEt/qBPg9OmaTp77ZGg7sZxCLUhEJLEITJRnZpL+n/GYk0+94+LhibWw6GfIY4RvekGnKmmKI5SBtMS5t+WSdWTGuGI0Gp06Tu3ERCQ3c6uC+a1Y6LzUUhi1SF5L0u1kYdSRNKI71TSdPIfIlHZi169f58MPP2Tr1q2cP3+emJiYJMcYDAZOnjzp7i1ERLIsR8VX4jDzPE2Zzt6kA3i8GZ5cZ0m6vQywrIfLSbd1mrmVKp5KSkJDQz0dgohIluZWBfM0diOpQ4AemOdSbiXef//9N02bNuXkyZP4+PjYMv07d+5w69YtwNLD29vbxeIEIiLZRGX8MP77htvKCwPP0ZhePMASjjCT/ZYdZjM8/R18EQ5GA3zVDbpVc+l+BuA92vIiW1XxVJzSokULT4cgIpKluVzBPB26kTzJWi0Ty6Wcm4eWyOuvv87JkydZtGgR//zzDwCjR48mOjqa/fv306hRI+69915+/fXXdA1WRCSrCMSXuXTC69/um9ZEeBMnaczn9kn3/30Pnx60ZM+LHoXeNVy+33u05XmacYZRhDKQM4xiCPXS7wtJjvDxxx/z119/eToMEZFsobIrs8bS2I3EKh44QaTL50n251bivWHDBtq0aUO/fv2StBlr2LAh33//PWfOnGHSpEnpEqSISFY0hHp2iXAtStm3EjObYexm+DDMknR/0QX61nLrXg0oA1gS/pZU0JNycWjkyJGUK1eOhg0b8tZbb3HkyBFPhyQikiVZu5L0pWbqB6ehG0liRtAysVzKrcT7woUL1K1b1/bZy8vLNsUcoFixYnTo0IHly5enPUIRkSwsEF8q4ccs9tOIz+2T7he3wox9ls9zO8GgOm7dQ2u5xVlhYWFMnDiRO3fu8Morr1CnTh0qVqzI2LFj2bFjB/Hx8Z4OUUTEoyIw8QKbKcsMWrOQr0jlAWUau5EYEv3+Dm05TiQRmNyKX7Ivt9Z4+/r6Ehsba/tcrFgxIiIi7I7x8fHh0qVLaYtORCSLS7bn56uh8N4ey+8fPwxDXZsWbi2kprXc4or69etTv3593njjDc6cOcPq1atZu3Yts2fPZubMmfj5+dGxY0e6dOlCu3btKFiwoKdDFhHJNC5XMLd2I/n6F0s3khU94eHKTt/PCwN7GcIZrgHwJybGs9XWhnQunbRsLBdxq51YUFAQAQEBrF69GoD27dvz888/8+uvv1K8eHFu3bpF7dq1MRqNHDt2LN2DzmxqQSKSe1l7ewI0pawtAbZu783KpCdN3gGv/WD5fdZD8H+NXbrne7TlMWpwgki1G8mhMntciYyMZP369axZs4YtW7YQHR1N/vz5adOmDV27dqVjx46UKlUqw+PwJI3lIrmbozagKYo3w7C1lsKo1m4k3R9w+n7WB+fWxDq5NqRnGKVxPhvL8HZi7dq1Y8aMGdy8eZOCBQsyfPhwevToQe3atQkKCuLQoUOcOXOGt956y60vICKSFczjkN2abQPwLm25TDTvs8fx0D3lx/+S7mltXU66p/5bRA3QQCzpxs/PjwEDBjBgwABiYmLYsmUL3377LevXr+e7777DaDTSpEkTdu3a5elQRUTSjXUdd2X8XKtg7qgbiQtJ93J6EJTgYT0k34b0BJEa73MJt954X7hwgZ07d9KmTRtKlCgBwPvvv8+bb76JyWSiQIECPP3007zzzjt4eXmle9CZTU/JRXKfCEyUY4YrTUbg/T3w/BbL71PawIsPunxfPf3OHbLKuGI2m9m7dy/ffvsta9eu5ejRox6LJaNllX9zEckcCaeVGzHQjWqs5LfUT7R2I7EWRl3c1aXCqO/Rlhf+fYCekN5450yujC1uJd7JiYuL48qVK5QqVSpJtfPsTIO1SO4Tymlas9D5E2bvh+c2Wn6f1BJedb+H8nJ60BPXW45J9qFxJfPp31wk93Dr4Tn8141kxr7/upG4UBjVAJxldLKJ9DwOMZx1xGFOMhVdsqcMn2qeHC8vL/z9/dPzkiIiHlEZP1uBs1R9EvZf0v1y8zQl3QC9WUkUdzQYi0ueeOIJt84zGAzMmzcvnaMREfGcWex3L+mesC1N3UjMkOLU8SHUoz0VVcMll3Lrjffu3btZtWoV48aNIyAgIMn+CxcuMHXqVHr16kWTJk3SJVBP0lNykdwp8Rpvhz47CE+ut/w+vpllirkLM34m0px32UVcorto+lnOlhHjitHoVodQDAYDcXFx6RJDVqaxXCR3cLmImtUr2+HNHy2/f/wwPNXQ5Xtr7M59MvyN9/Tp0zl8+DDTp093uL906dKsX7+ev/76i2XLlrlzCxERj0hYiMX6ZHov57jKTZ5ig/3BC8Jh+L9J9+gmLifdA6nNW7ShNv5JqqOr4Iq46vTp054OQUTE41wqomb1xo7/ku5ZD7mddKv9p6TErcQ7LCyMNm3apHhMcHAwW7ZscSsoERFPSFyIxdpfsye+hJIoqfnqMDzxrWVe2bON4P12TiXdPahGWXx4jJo0JJAITABJprV7YaASfun23STnK1++vKdDEBHxuPfZ49oJ7+yCV3+w/O5GN5Ll9KAkhTR1XFLlVuJ9+fJl7rnnnhSPCQgI4PLly24FJSKS2SIw2ZJugHjMDGcdRchLU8rar/le9gsMWGP5MKK+5em4E0m3FwZm8JBtYE6Y6Bv4L/nWU3MRERHXhRHBdxx3/oT391jWdYNl1trYpi7dzwtDkrZhIslxK/EuWrQoZ8+eTfGYP//8k8KFC7sVlIhIZkuuv2ZvVmLEwGPUsOz95ij0/QbizTCkLnz0iFNJtzFRMp040bcm3F/TXYO4pDtr15GYmBiH+8uVK5fJEYmIpL8fSTk/sTN7/38tQCe1dLkFqB6Si6vcSrybNGnC6tWrOXfuHGXLlk2y/+zZs6xZs4bWrVunOUARkcxQGT+MGByuC4vHzFccgbW/Q++VEGeGAbUtFU+Nzq3p3scQGhJo+5xcol+SQhrEJd0cPHiQiRMnsnPnTu7cuePwGIPBwN27dzM5MhGR9BWBids4+d+yNHQj6UE1nqGRppaLy9wqgTpmzBhu3rxJs2bNWLRoERcuXAAs1cwXLlxIs2bNuHXrFmPHjk3XYEVE0lsEJtv67bl0wotkEukNx6HHcrgbD4/VgC86O510A0QTa/fZmugnpHXdkp7Cw8Np3rw5e/fupV27dpjNZmrVqkW7du0oUaIEZrOZFi1a0L9/f0+HKiLiFusY/jLbKMcMXmJ76id9dhCe/rdY6rimMLmV0/cbTWNW0JuWVFDSLS5z6413cHAw06dPZ+zYsQwePBiwPDG3diYzGo3MmjWL4ODg9ItURCSdJS6m1p9aSdp6AbD5JHRbBrHx0PMBWNQVvJx/bmmEJAl1IL7MpRPDWUccZk1Zk3T3xhtvALB//36qVauG0Wika9euvPrqq7aH4ytXruSLL77wcKQiIq5LOIY7LXE3kndCXOpG8hg1XQtSJAG3Em+A5557jlatWjFnzhzCwsIwmUwULVqURo0aMWLECGrUqJGecYqIpKsITHY9uuMxs5Cfkx64/TR0WQoxcfBoVfiqG+SxT7pr4896HmcW+5nmoJrqGJo6TKit7cpOEKkpa5Ludu3aRefOnalWrZptm/UBeYECBfjwww/Zs2cPEydOZMmSJZ4KU0TEZWFE2I3hTknYjWRkQ6e7kVg9TGW7JWMirnI78QaoVasWH3/8cXrFIiKSoRL26J7F/tQH7J1/Qqev4fZd6Hg/LOsB3l5JDjvMJQCeozHT2Wv39N0LA8+RfGuSQHyVcEuGMJlM3HfffbbP3t7e3Lhxw/bZaDTSsmVLvv76a0+EJyLiFuubbpeS7oTdSIbXh9kdXEq6m3AP39HXxUhF7Lm1xnvPHuf6482YMcOdy4uIpLt5HKI8M2nNQsoxI/U+n7vPwsNfwc1YeKgSrOwJeZMm3WAZx08QaZs+bl0nrunj4kmlSpXin3/+sX0OCAjg+HH7Nju3b9/m5s2bmR2aiIhbEncEcUribiQfO9eNxMoArKCX68GKJOJW4t2pUyeOHj2a4jEzZ87k+eefdysoEZH05Kh1V4pD9v4I6PAVRMdCyH3wTS/Il/IEoUJ4A5bp42cYRSgDOcMohlAvfb6EiIseeOABfv/9d9vnZs2asXnzZvbu3QvA0aNHWb58OVWrVvVUiCIiLnHUESRFaehGApYH6J/RWQ/QJV24lXgXKFCAhx56iL/++svh/tmzZzNmzBiCgoLSFJyISFpFYGI5vzo/UB84D+2/hOt3oOW98G0fKOCd6mkJq5YH4quKp+JxjzzyCDt37rR1Hhk/fjxms5kHH3yQkiVLUrNmTa5du8bEiRM9HKmIiHMK451c75Gk0tiNZBSN2csQPUCXdONW4r1x40aioqJo164dkZGRdvs++OADRo0aRZMmTdi4cWO6BCki4g7r9PKxbHbuhPCL0G4xmGLgwXKw7jEomHrSbSBp1XIRTxsxYgR//fUXxYsXB6B27dps27aNhx56iBIlShASEsK6devo2rWrhyMVEUlZBCZeYDON+dy5x+hp7EYCMJP9NGEe8zjkVswiibmVeNeoUYN169Zx5swZOnbsyK1btwD48MMPee6552jUqBGbNm2icOHC6RpsYlOmTKFhw4YUKVKEUqVK8eijj9pNqwPL+rVnnnmG4sWLU7hwYbp3786lS5cyNC4R8TyX14EduQQhi+Cf2xAUCBseh8J5nTp1As2TvN229haNwORq6CLpwtvbG39/f/Lm/e9/x02bNuW7777j6NGjbNy4kUceecSDEYqIJM86jv4fGyjLDKaxx7kR3YluJM6Kx8xw1mksl3Th3v8KgQcffJCvv/6asLAwevTowaxZs/i///s/GjRowKZNmyhSpEh6xunQjh07eOaZZ9i3bx9btmwhNjaWdu3aER0dbTtm9OjRrFu3jhUrVrBjxw7Onz9Pt27dMjw2EfEsl9aB/fY3tFkEV29BwzLwfV8oks+pU2tSirdoY7ctYSG38szU03IREREXJBxHP+An5090shuJK+Iwc4LI1A8USYXBbG3q6aZ58+YxbNgwDAYD9erVY9u2bfj4+KRXfC75+++/KVWqFDt27CA4OBiTyUTJkiVZsmQJPXr0AODYsWNUq1aNvXv30qRJE6euGxUVha+vLyaTyWPfTUScY20ZVhhv56ak/X4FWi6EizegXmnY2h+KFXD6fl4YOMMo2xvvCEyUZ2aSlmIJjxHJjHFl9+7drFq1inHjxhEQEJBk/4ULF5g6dSq9evVyejzMzjSWi2QPjsZRp+w5Z1kuFv1vN5I1vVMtjGoVQgWeowm3iKUPqzSGi9NcGVuc+l/jzp07k91XuXJlOnfuzK5du3j55ZcJDw+32x8cHOzMLdKFyWSZBuLnZ1lrefDgQWJjYwkJCbEdU7VqVcqVK5di4h0TE0NMTIztc1RUVAZGLSLpxdrbMx4zBlKpXA5wIhJaL7Ik3bX8YXM/l5Ju+O9JuHVAdvSmPfExIplh+vTpHD58mOnTpzvcX7p0adavX89ff/3FsmXLMjk6ERHHXK5cDpZuJA996VI3koTm86htjI7iDsNZRxxmtQWVdOXU/yJbtmyJIZV+d2az2eEU7ri4OPcic1F8fDyjRo2iWbNm1KhRA4CLFy+SN29eihYtanesv78/Fy9eTPZaU6ZMYdKkSRkZroikowhM7OEcw1hrG6pTHbJP/wOtF8L561C9pOVNd/GCLt/bC4NdYbXK+GHEkORpuYqvSWYLCwujTZs2KR4THBzMli1bMikiEZGURWDiGH+7dtJB97qRJJTw4fgQ6tGeipwgkkr4KemWdONU4v3qq6+mmnh72jPPPMMvv/zCrl270nytCRMmMGbMGNvnqKgoypYtm+brikj6S/iW22lnTZY33eeioGoJ2DYAShZy6/7vEGI3KAfiy1w66Wm5eNzly5e55557UjwmICCAy5cvZ1JEIiLJm8chuwfoTgm/CG1d70aSkJGknUkC8dW4LenOqcT79ddfz+Aw0mbkyJGsX7+enTt3EhgYaNseEBDAnTt3uHbtmt1b70uXLjlc72aVL18+8uVzrrCSiHiOy5XLASKioNVCOHMNKvtZkm5/9zswjGcrxShg1+dTT8slKyhatChnz55N8Zg///wzwzuQiIikJgITQ1nr2kkJu5E0ca0biZUBmEtnjdOSKdyuap4VmM1mRo4cyerVq9m+fTsVKlSw21+/fn28vb3Ztm2bbdvvv//O2bNnCQoKyuxwRSSdubwO7MJ1y/TyU//AfcVg+0Aok7YODMm1GgnEl5ZU0GAuHtOkSRNWr17NuXPnHO4/e/Ysa9asoWnTppkcmYiIvVnsd+2ExN1INjrfjQSgHzVZTg/OMtruwblIRnIq8U7Ynstd6XGNxJ555hm+/PJLlixZQpEiRbh48SIXL1609RX39fVlyJAhjBkzhtDQUA4ePMjgwYMJCgrKFRVcRXIqa2/PwnhjxMllMJduWKaXH4+E8r6wfQAEOlfZOLV7qNWIZEVjxozh5s2bNGvWjEWLFnHhwgXAUs184cKFNGvWjFu3bjF27FgPRyoiuVUEJpbzC++zx/mTfr9iSbr/vgl1A2BTP/DN79J9h1CPntTQw3HJVE5NNa9QoQIvvPACTz/9NIUKubYOcu/evUyaNIlmzZrxyiuvuBVkcj755BPAUvwtofnz5zNo0CAAZsyYgdFopHv37sTExNC+fXs+/vjjdI1DRDJPwjVgBqAHD7CC31I+6e9oyyB97Iol2d4+EMoXdep+RmAfQ4gmlkJ4c4Zr9Gal3Xt2FU+TrCg4OJjp06czduxYBg8eDIDBYMDaRdRoNDJr1qxM7T4iImLlVo2WxN1ItrjWAhQsD9M1ZosnONXHe9SoUXzyySfkzZuXbt260aNHD5o0aULJkiWTHHv37l1+/vlntmzZwldffcVvv/3GAw88wPz582nQoEGGfImMpt6fIllDBCbKMcO1witXb1oG6cOXLNPKdwyCSs4PuO/RlhdoZrdtHoeSFE/TVDVxRWaOK4cPH2bOnDmEhYVhMpkoWrQojRo1YsSIEbYuILmBxnKRrMOtXt2n/4EWCyyFUauXhNCBLhdGNQCf0VljtqQbV8YWpxJvgOPHj/PGG2+wYsUK7ty5A8A999yDv78/RYsW5fbt20RGRnL69GliYmIwm8088MADjBkzhkGDBmE0Zt/l5BqsRbKG5fxCb1Y6f8I/tyBkMRy6AP6FLEl3lRIu3TOUgbSkQpLtEZhUPE3clpXGlbi4OLy8vDwaQ2bISv/mIrldKKdpzULnTzhrsiTdZ65ZupH8MNClwqhNCaQ/tehIFY3Zkq5cGVuc7ixfuXJlFi1axMyZM1myZAnbtm1jz549HDx40HaMt7c3NWrUoEWLFnTt2pXmzZu7/y1EJFeLwMRxIqnsbmJrum3p63noApQsaJle7mLSndJ0NLUakazuo48+4plnnknxmLi4OPr06cOKFSsyKSoREajsylTvNHYjMQLL6KkxWzzO6cTbys/Pj5EjRzJy5EgAYmNjuXr1KgUKFMDXV/+DFpG0S7juy4iBuf9O5a5AUecucD0GOnwFYeeheAHLIP1A0qUxqXk3UY9ukezk//7v//D396dHjx4O98fHx9OnTx+++eabTI5MRHIr60P1bZxy7oQ0diNRuzDJSlxOvBPz9vZOsSe2iIgrEvfmtrbrak9FTnMt9QtE34FHlsDeCCiWH7YOgJr+LsVgAN6lLc8nWtstkp08+OCD9O/fn+LFi9OqVSu7ffHx8Tz22GOsWrXK9iBdRCQjuVxMLQ3dSACGU5+XCVbSLVlG9l14LSI5kqPe3HGY6c/q1Nd334yFjl/Dj2fBNx9s7g91XHswaMTAfoYmKagmkt2sW7eO+++/n65duxIeHm7bHh8fT9++fVmxYgVPP/00s2fP9lyQIpIrJH6onqo0dCMBywN0Jd2S1SjxFpEspTJ+Dvtm/8CZlE+8fRe6LIUfzkCRvJa+ng3KuHx/M2YOc9nl80SyGh8fHzZt2kSxYsXo0KEDp06dwmw28/jjj7Ns2TJGjBjBhx9+6OkwRSSHi8DEWDY7n3RfvWkpjPrr35Zp5aEDLdPMXWAGThDperAiGUiJt4hkKYH4MpdOeDlIvpMVcxe6LoOtp6CQN3zfFxoHunV/MzCcdURgcut8kawkICCATZs2ERcXR7t27ejVqxfLly9n2LBhfPzxx54OT0RyuHkcojwzWc6vzp3wzy1o96WlBah/Icv0chdagFp5qVe3ZEFKvEUkyxlCPc4wiv7USv3gO3HQcwVsPAEF8sB3j0Ozcmm6fxxmPSmXHOP+++9nw4YNXL58mW+++YahQ4fy6aefejosEcnhwohgGGudf9Odxm4k1sf1Xhj4lE6aZi5ZTpqLq4mIZIRAfAkikMUcTv6g2DjosxLW/QH588D6x6HFvWm+t56US3Y0efLkFPc3atSI8PBwypQpY3eswWDglVdeyejwRCQXmcchhrHW2ZQ7XbqRLKMHJSlEJXfbkIpkMIPZbHb6/ydyK1cao4tI+onARFlmON55Nx4eXwUrfoO8XrDuMWhX0elrG7BMKzcC3ajGao4Rh9n2pHwI9dLjK4g4lBHjitHo3iQ2g8FAXFxcusSQlWksF8kcEZgoxwznk+7oO5ak+8ezlm4k2we6XBjVCwNnGKWEWzKdK2OLW2+89+/fT+PGjd0KTkQkMWtfz8rOPqWOi4eBayxJt7cRVvd2KekGS+K9jB4EUZZAfInAxAki9aRcsq3Q0FBPhyAiwjp+dz7pvhkLndLWjURTyyW7cCvxDgoKombNmgwbNox+/fpRtGjRdA5LRHKLhH09jRiY++/b5ghMdGVZ0hPizTBkLSw5AnmMsKInPFzZ5fvGAyUpZBuoA/HVoC3ZWosWLTwdgojkcvM4xNNscO7g23fh0aUQesbtbiSf8DAdqaLxW7IFt+al9evXjxMnTvB///d/lClThgEDBvDjjz+md2wiksMl7usZj5nhrGMquynPTA5w3v6EeDM8uQ4W/gxeBljaHbpUdeveWsctkj199NFH3HvvveTPn5/GjRvz008/eTokkVwtAhOhnCaMCIay1rmTrN1ItrjfjaQH1RhBIyXdkm24lXgvWrSI8+fP88EHH1C1alW+/PJLWrZsSdWqVXn//fe5cuVKescpIjnQcSKTVDuNw8x4tiStgmo2wzPfwbz/gdEAX3WD7g+4fe93CNFgLZLNLFu2jDFjxvDaa69x6NAhateuTfv27bl8+bKnQxPJlaztwlqzkEZ87txJ6dCN5FkasYLebkQs4jlutxPz9fXlmWee4dChQxw4cIAnn3ySS5cu8cILLxAYGEjv3r3ZunVresYqIjlMZfwwJurXbS16Zsdshuc2wpyDlgMWPgq9a6Tp3g1wbTqbSFb30EMPERYW5ta50dHRvPPOO3z00UfpHFX6mj59OsOGDWPw4ME88MADzJkzh4IFC/LFF194OjSRXCcCk2vtwiBpN5J1j7nVjeQjwpjHIZfPE/GkdOnjXa9ePT755BPOnz/PggULKFGiBCtXrqR9+/bcd999vPfee1y/fj09biUiOcjLbE8yYDtMup/fDB/8O510Xmfo50R/7xRomrnkRH///TdNmjShVatWzJ8/H5PJlOo5+/btY+TIkZQvX5433ngDf3//TIjUPXfu3OHgwYOEhITYthmNRkJCQti7d2+S42NiYoiKirL7EZH0s4dzrqTclm4kfb+B1ccs3UjW9IY297l1b+vStAhS/++cSFaRbn28//nnHxYtWsTnn3/O+fPnMRgMNGvWjKNHj/Liiy8yc+ZMvv32Wxo2bJhetxSRbCyMCBbyc8oHmc0wYRtM32f5PLcjDK6bpvuq+qnkVAcPHmThwoVMmjSJIUOGMGzYMKpUqUL9+vXx9/enaNGi3L59m8jISH7//XcOHDjA9evX8fLyok+fPrz55puUK+fadM/MdOXKFeLi4pI8HPD39+fYsWNJjp8yZQqTJk3KrPBEcqSUuo5c5abzF3LUjaR9pTTFFoeZE0RqPJdsI82Jd2hoKJ999hlr1qzh9u3blCxZkhdeeIHhw4dz3333ERMTwxdffMG4ceN49tln2bdvX3rELSLZRMJBGyzrugvjzXDWp37yaz/Au7stv3/0MAyr7/L9jRgYQxC9eIBoYtUuTHK0gQMHMmDAADZs2MD8+fP54Ycf+PLLL5McZzQaqVWrFl27dmXo0KGULl3aA9FmrAkTJjBmzBjb56ioKMqWLevBiESyl+S6joBlbE9SADU5aexGMpQ6PEkDmjDPbpacZq9JduNW4n3p0iXmz5/PvHnzOHXqFGazmRYtWjBixAi6deuGt7e37dh8+fLx1FNPceLEiSy/dkxE0lfCQdvh2u2UvLED3thp+X1me3ja9dkyRmAfQ2iIa5VSRbIzg8HAI488wiOPPALA0aNHiYiI4OrVqxQoUICSJUtSvXp1fH2z1wOoEiVK4OXlxaVLl+y2X7p0iYCApH1/8+XLR758+TIrPJEcJbmuI+2pyCZOOl+9PB26kbxGKwLxZS6dGM464jBr9ppkS24l3oGBgcTHx1OsWDFGjRrFk08+SZUqVVI8p2TJkty5c8etIEUk+7C+4S6MN8NYa0u2XUq639kFr/5g+X1qW3iuictxGIG5dFbSLbletWrVqFatmqfDSLO8efNSv359tm3bxqOPPgpAfHw827ZtY+TIkZ4NTiSHSa7ryF7OOZ90p0M3kvdoa0uuh1CP9lTkBJGavSbZkluJd+PGjRkxYgQ9e/Z0+mnyiy++yIsvvujO7UQkm0jTG26r6Xst67oB3m4Nzzd1+RJGDHrTLZIDjRkzhoEDB9KgQQMaNWrEzJkziY6OZvDgwZ4OTSRHsXYdSTy1+4qz67rToRvJSzTnBZrZbQvEVwm3ZFtuJd67du1K7zhEJJtLPC3NraR79n4Yu9ny++stYEJzly9hnX6mpFsk5+nduzd///03r776KhcvXqROnTps3LgxS1djF8mOHE3tfocQvud46iensRuJEXiHtkmSbpHsLt2qmotI7uZoWppLPgmzPB0HeKk5vNrC6VMfpCzTaa/iaSK5wMiRIzW1XCQdJVe5POHU7jDO8wJbUr9YGruRDKc+LxOscVxyJLcS79atW6d6jNFoxMfHhypVqvDoo4/SuHFjd24lItmEo2lpTvv8EDy9wfL7uKbwRiswGJw+fRfn2MGfPO/g6XhKrVBERERys5Qql4PlzfcFrjPOmaQb0tSNpB81mUMnF6IXyV4MZrPZ5b+SjUaj5WSDAUenJ95uMBgYPHgwn3/+eRpC9ZyoqCh8fX0xmUz4+Ph4OhyRLCvhAO60heEw+FvL3PRRjWF6e5eSbisDsJQeNKWsLcFO7Q8KEU/RuJL59G8uYi8CE+WZmWQd9xlGEYgvEZh4k518ykHnLvjGjv8Ko85s73Jh1HOM1gNyyXZcGVuM7tzg1q1bdOrUiWrVqrFkyRL+/PNPbt++zZ9//smSJUuoXr06nTt35ty5c2zevJl69eoxf/58PvnkE7e+kIhkTRGYCOU0EZgAy7S0x3CheMqSI/8l3c80dDvpBsslerOS8sxkHoeSbYVijVVERCQ3S65y+QkimcchyjLD+aT73bR1I/mczkq6JcdzK/F+7bXXOHLkCPv376dPnz6ULVuWvHnzUrZsWfr06cPevXs5fPgwH3zwASEhIWzZsoWSJUsyf/789I5fRDwgAhMvsJlyzKA1C+2S3SUcce4iy3+F/qstGfOT9WB2hxSTbmfTcWuCvYdzyf5BISIikttZl4gl5IWBQng73zIMLN1IXvy3G8lbrncj+YSHNRtNcgW3Eu8lS5bQrVs3ChUq5HB/oUKF6NatG19//TUARYsW5aGHHuLo0aPuRyoiHpcw4Z7GHltamzDZdWqS+eqj8PgqiDfDE3Xgk46WHp/JMGDp5en17x8IXhjoyQNJ/mCwivu3nZmjPygq4edMhCI5wt27d5kxYwaNGjXCx8eHPHn+K+0SHh7O008/zR9//OHBCEXEU6yVyxOOre8QwgS2OX+RDxJ1I5noWjcSA9CRKi6dI5JduVVc7e+//yY2NjbFY+7evcvly5dtn0uXLk1cXJw7txORLCC19dtxmAnldOoXWvc79F4JcWboXwvmdkox6QbLS/FY4lhCdwxA0L/ruCMwsZdz9GFVkjVqQZRN0grlUzppKpvkGrdu3aJdu3bs2bOHEiVK4OPjQ3R0tG1/hQoVmD9/Pn5+frz55psejFREPMWtyuVWcw7A/7nXjQQsSfdnmmIuuYhbb7wrVqzIihUruHr1qsP9V69eZfny5VSsWNG27fz58/j56U2TSHaUeL10cuakthbs++PQYwXExkOfGjC/C3g595+hiWynNyvpwyo2cRKwPK3vSY0kT+ytCfYQ6nGGUYQykDOM0lQ2yVXefvttdu/ezZQpU7h48SJDhw612+/r60uLFi3YtGmThyIUkawgEF8q4cd4V5Luzw/BU99Zfn/BtW4kfanJcnpwltEalyVXceuN97PPPstTTz1FvXr1GDt2LM2aNaNUqVJcvnyZ3bt38/7773Pp0iVee+01AOLj49m+fTsNGzZM1+BFJHOkuUc3wJaT0HUZ3ImDHg/A4q5OJ90JWae1t6ei7Sl5wif2ift4B+Krp+mSKy1btoxWrVoxbtw4wNJhJLH77ruP//3vf5kdmohkMceJdH6UXxgOT66z/D6qMbwb4lJh1KHUoyUVXA1RJNtzK/EePnw4f/31F1OmTGH06NF2+8xmM0ajkQkTJjB8+HAAIiMjef7552na1LViCyKSNaSpRzdA6GnovBRi4qBLFVjSDfK4NeEG+K9ImhJskeSdPXuWrl27pnhMkSJFMJlU6V8kt4rAxB7OcQLHs1iTSGM3EtVakdzMrcQbYPLkyfTv358lS5Zw+PBhoqKi8PHxoXbt2vTp04f777/fdmyJEiV47rnn0iVgEcl81gIsLlU5tdr5J3T8Gm7fhUcqw7Ie4O2Vpng0cIukrkiRIna1Vhw5efIkJUuWzKSIRCQrmcpuxrkyvdzFbiSJGVVrRXI5txLvRYsW4e/vT/v27W3TyUUkZ6tFKQzg2jvvPefg4a/gZiy0rwgre0E+t5/3AahImoiTmjRpwrp167h27RpFixZNsv/cuXNs2LAh1bfiIpLzTHM16XaxG4ljZtpTMfXDRHIot+Z6DhkyhI0bN6Z3LCKSRU1lN4353LWk+6e/4KEvIToW2lSA1b0hv/tJtwFYTg8VSRNx0gsvvMA///xDmzZt2L17N3fv3gXg5s2bbNu2jfbt23P37l3GjBnj4UhFJDNFYHIt6XajG4kj8cAJIl0+TySncOuv4NKlS9sGcBHJ2Vx+Kg5w8Dy0WwzX70CL8rD2MSjg7dIl6lOacC7atQLrSQ3X4hDJxYKDg/nwww957rnnCA4Otm0vUqQIAF5eXnz88cfUr1/fUyGKSCaLwMRcDjr/ID0N3UgS0zIxye3cSrw7d+7Mli1biImJIV++fOkdk4hkERGYGM9W1076+SK0XQymGHiwHKx/HAq6lnQDhHORvQwhmtgklcpFxDlPPfUULVu2ZM6cOezfv5/IyEh8fHxo3LgxTz/9NNWrV/d0iCKSCSIwMYv9vM8e55PudOpGApYptlomJrmdW4n3W2+9xd69e+nWrRvvvfeeBm6RHCYCE8eJ5G+iXatk/stlCFkM/9yGJoGw4XEonNetGOIwE02sWo6IpFG1atWYNWuWp8MQkUxmHcsPcJ7xbHFtuVg6dyNZSg/NWpNcz63Eu27dusTExBAeHs7GjRvJnz8/pUqVStIj1GAwcPLkyXQJVEQynltPxK2O/g1tFsGVm9CgDGzsC0XcnxGjKWkiIpLbWZPnyi7O/JrHIZ5knXttQNO5G4kXBoIo6/b5IjmFW4+u4uPjyZs3L+XKlaNcuXKUKlUKsPTwTvgTHx+frsGKSPqIwEQop4nAZPv8Apspz0ymOUi6Uy2h8sdVaL0ILkdDnQDY3A9887scl/U+qlwukna7d+9mzJgxXLx40eH+CxcuMGbMGPbt25fJkYmIM+ZxiPLMpDULKc9M5nHIqfMiMLmfdKdzNxK1EBP5j1v/n3TmzJl0DkNEMkvCp+BGDPSnFov4OcXhOcWh+2QktF4IF29AzVKwtT8UK+ByXEZgH0O1plsknUyfPp3Dhw8zffp0h/tLly7N+vXr+euvv1i2bFkmRyciKUmcPMdjZjjraE9Fh+Njwjfjx4l0L+lOYzeSxC1HLeP6EBoS6HosIjmQ+4s1soidO3fSqVMnypQpg8FgYM2aNXb7zWYzr776KqVLl6ZAgQKEhIRw/PhxzwQr4mGOBvKFqSTdKTpzDVothL+uwwMlYesAKF7QrUv1pzYNCaQlFZR0i6SDsLAwHnzwwRSPCQ4O1htvkSzIUfIch9lhO67Eb8aX8QvG1Oeq2Tt0IU3dSF6iOZ/RGa9/7+uFgbl0VtItkkCaE+/ffvuNb775hsWLF6dHPC6Ljo6mdu3afPTRRw73v/fee8yePdtW0bVQoUK0b9+e27dvZ3KkIp7n9lNwR86aLEn3uSioUhy2DYBShdy+3Jcctk19F5G0u3z5Mvfcc0+KxwQEBHD58uVMikhEnFUZvyTJs6PaJ44eqH/KQdfG+p8vQsgiSzeSZmXd6kYyggYMoR5nGEUoAznDKIZQz6VriOR0bifeYWFh1KlTh5o1a9KzZ08GDRpk27dz504KFizI2rVr0yPGFHXo0IE333yTrl27JtlnNpuZOXMmL7/8Ml26dKFWrVosWrSI8+fPJ3kzLpIbOBrI3fJXlGV6+ZlrUMkPtg+EgMJOn+4oguSe5IuIe4oWLcrZs2dTPObPP/+kcGHn/39XRDJHIL7MpZPdG2RHa6XT/EA9STeSvm51I7GO34H4auaaSDLcSrx//fVXWrduzenTpxk9ejQdOnSw29+8eXNKlCjBihUr0iVId50+fZqLFy8SEhJi2+br60vjxo3Zu3dvsufFxMQQFRVl9yOSEwTiSw+qpe0iF65bCqmd/AcqFIXtA6BMEZcuMZHmTj3JFxH3NWnShNWrV3Pu3DmH+8+ePcuaNWto2rRpJkcmIs5w5g1ymh6oO+pG4uN6NxKN3yLOcSvxfu211wA4ePAg06ZNo2HDhnb7DQYDQUFBhIWFpT3CNLBWcvX397fb7u/vn2yVV4ApU6bg6+tr+ylbVi0QJHtLWMX8edLwR/alG5ZB+o+rUM4XQgdCWdeeaj9LI96kjVNP8kXEfWPGjOHmzZs0a9aMRYsWceHCBcBSzXzhwoU0a9aMW7duMXbsWA9HKiLJSe0NsvXNuMvJdzp1I9H4LeI8t6qa79ixg+7du1OpUqVkjylXrhwbN250OzBPmjBhAmPGjLF9joqKUvIt2VbiKuZz6cRAarOQn1270JWbluloR69AoI8l6S5f1OV4uv37xn0I9WhPRU4QqSrmIhkgODiY6dOnM3bsWAYPHgxYHoybzZZpqUajkVmzZhEcHOzJMEUkjYZQjz+5xhvsdO6EdOhG8hLNCeE+jd8iLnAr8b5+/bqtd3dybt26RVxcnFtBpZeAgAAALl26ROnSpW3bL126RJ06dZI9L1++fOTL5/pUG5GsxlHRlSdZx7f0cS3xjrxlKbzyy2UoXdgyvfy+Yi7HYwS76WiB+GrAFslAzz33HK1atWLOnDmEhYVhMpkoWrQojRo1YsSIEdSoUcPTIYpIOmhEyoUUbdKpG8k77GIEDTSGi7jArcS7bNmyHDlyJMVjDh06RMWKFd0KKr1UqFCBgIAAtm3bZku0o6Ki2L9/P0899ZRHYxPJDI6KrsRjphNfO3+Ra7ctLUZ+vgT+hSyF1CoXT/U0IwbeIYTxbLFFYAY2cVKVTkUyUa1atfj44489HYaIpLOEvbt38GfqJ6RjNxJrQVQl3iLOc2uNd8eOHdm8eTNbt251uH/58uXs27ePRx99NC2xOeXGjRuEh4cTHh4OWAqqhYeHc/bsWQwGA6NGjeLNN99k7dq1HDlyhAEDBlCmTJlMiU3E09Jcxdx0G9p/CQcvQMmClkG6agmnTn2XEB6jBoYE9zcDw1mntmEimcDLy4u+fft6OgwRyQAJe3eXZQbT2JPyCWnsRpKYEQOFcK3lmEhu51biPXHiRMqUKcPDDz/MsGHDOHDgAAAff/wx/fv35/HHH+fee++1WyedUQ4cOEDdunWpW7cuYCkmU7duXV599VUAxo0bx7PPPsuTTz5Jw4YNuXHjBhs3biR/ftcLSIhkN64WXalKgqT6egw8vAR++gv8Climo1VPeYlJYo7euKttmEjm8PHxUX0SkRwmAhPL+YWhrHW+jVg6dCNJLB4zTZjHPA6l6ToiuYnBbK2y4qJTp07Rv39/h225GjduzNdff829996b1viyhKioKHx9fTGZTPj4+Hg6HBGXLeB/DOZb50+IvgMdvoIfz0LR/JZBum7p1M9LwIiBfQyhCfPs/jjwwsAZRml6muRqmTGutG/fHqPRyPfff58h189uNJZLdpewWKrTLt2wTC8/esXSjWTnILcKo1oZwO7uGtMlt3NlbHFrjTfAfffdx+7duwkPD2ffvn1ERkbi4+ND48aNk7QXExHPsK7/OsU/zp90MxY6fW1Jun3yWVqMuJh0g+VpeDSxzKUTw1lHHGa1HRHJRK+//jotW7Zk0aJFDBgwwNPhiEgaJC6W6pR06kZi1YvqLOdXu21a6y3iPLcTb6s6deqkWCFcRDxjHocYxlpXhmi4fRceXQqhZ6BwXtjUDxo6WSk1ES8MVMKPllRQ2zARD9iyZQstW7Zk8ODBfPDBBzRs2BB/f38MBvulJwaDgVdeecVDUYqIMxwt3UpROnUjsfLCQOUEXUkSbq/kYLuIJOX2VPPcRNPTJDuJwMQ6fudpNrh2Ysxd6LoMvj8BhbxhYz94sJxbMVjfbKt6uYhjmTGuGI3OlXExGAweb/+ZGTSWS3aTsGo5QHlmOpd8X7ttSboPXrB0I/lhkNOFUQGW04OdnOUjfsKMZUyfkqhLidV7tOUFmjl9bZGcJlOmmv/999/Mnz+fsLAwrl275nDQNhgMbNu2zd1biIiL3HrLDXAnDnqusCTdBfLAd4+7nHQbgXdoS0PK6M22SBYQGhrq6RBExE0J13MbMTCXTtQjgANcSPnENHQjAXiepkRxh48Jw8x/rUHL4evwb4t7NdaLOM2txPvw4cO0bt2af/75h5RemCeeziYi7kn41Du5hDYCk3tJd2wc9FkJ6/6A/Hlg3WPQ4l6nTvXCwF6GEE2skm2RLKZFixaeDkFE3JB4PXc8ZoayNvUT06EbSS8esCuKGo+ZF9nKB3Rw+XuIiD232omNHTuWyMhIXnrpJU6fPk1sbCzx8fFJfnLD1DWRjJawV2d5Ztpad0RgIpTTtp7Yx4l0Pem+Gw/9VsPqY5DXC9b0hjb3OX36aIJoSCAtqaCkW0REJB24vJ4bLN1IHlkCe85ZupFs6Q+1/F26xHDqc4NYh21AS1AwSWNSAxCEWhaKOMutN9579+7l0UcfZfLkyekdj4gk4Oip93DWEckt21orA/AubSnvauIbFw+D1sDyX8HbCN/0gvaVnD7dCDxHY9fuKSKZbvfu3SxYsIDw8HCioqLw8fGhbt26DBgwgAcffNDT4YlIIpXxw4jB+eTbUTeSeq51IzEALxMMkOTeXhgIoiyf0ZknWUs8lr8B5tJZD91FXOBW4p03b14qVqyY3rGISCKOnnrHYWYcW2yfzWD32SnxZhi6Dr46AnmMsKInPHK/06erLZhI9jB69Ghmz55tWxZmMBgwm80cPHiQefPm8dxzzzF9+nQPRykiCQXiy1w6OTe9PB26kSROopNrAzqEeupSIpIGbiXeLVq04MCBA+kdi4hgv57b5afezog3w/B1sCAcvAzwdXfoUtWpU4dSh77U1oArkg0sXLiQWbNmcf/99/Paa6/RqlUr/P39uXz5MqGhoUyaNIlZs2ZRp04d9fkWyWLaUxEDpDz6x9yFbstgyylLN5Lv+0KTQJfuM4L6vESw3ZieUoIdiK/GfxE3udVO7OTJkzRp0oTx48fz/PPPZ0RcWYpakEhmcVTFFLA9eU4zsxme2QCfHACjAb7qBn1qOH36JzzMCBqlPQ6RXC4zxpUmTZpw/vx5jhw5gq9v0j+UTSYTNWvWpEyZMuzbty9DYshKNJZLdhLKaVqzMPkD7sRBj+WWwqgF8liSbicLo1pNpDlv0SZtgYrkchneTuytt96iRo0ajB8/njlz5lCnTh2HNzIYDMybN8+dW4jkOsmt5z7DKJbQnd6sTNsNzGYYtdGSdBuABV1cSroNQEeqpC0GEck0v/76K0OHDnWYdAP4+vrSvXt3Pv/880yOTESSE4GJPZzjGb5L/qDYOHhslVvdSKym0pbn1X9bJFO5lXgvWLDA9vupU6c4deqUw+OUeIs4L7n13CeIpCll0zbl3GyGF7bA7J8snz/vDP1rO326AfhMRVREchy1/RTJPCm1Bo3AxCz28z57Uh7prd1IvjnqVjcS0Ow1EU9xK/E+ffp0eschkus5Ws/thcG2vupdQnjB1SJqYEm6J26D9/daPn/aEZ6o69IlDEmaiIhIVle9enVWrVrFG2+8QeHChZPsv379OqtWraJ69eoeiE4kd3G0lGwI9Wz7nCqklsZuJFbFKejyOSKSdm718S5fvrzTPyLiHGsVU69/k9zElcPLufu2+fUf4J3dlt8/7ABP1nf5EtZp79ae4SKS9Q0fPpyIiAiCgoJYtWoVV65cAeDKlSusXLmSpk2bEhERwVNPPeXhSEVytuSWkkVgIowI55LuNHYjsVLvbRHPceuNt4ikL+v0s/ZU5Ayj7CqJWqefTWOP6xd+cydM3mn5fUZ7eMbx1LKRNCKYclzlJk+zweE0N+u0d003F8keBg8ezP/+9z8+/PBDevXqBYDRaCQ+Ph4As9nMs88+y8CBAz0ZpkiOl9xSMuvU8lSloRtJQuq9LeJZTiferVu3ZtCgQXYtR/bv38/+/fv5v//7vyTHv/vuu7z33ntcvXo1fSIVyaFSmn42jd2MY4t7K7vf3QWvhFp+fy8ERjWx7TIAo2jM/RSnI1XsBmFv8vAka4lPdDnrtHcRyT5mz55Nz549WbBgAeHh4URFReHj40PdunUZOHAgzZs393SIIjmeo6VkRkh9PTdYlouN3ACf/8/SjeTLbtDjAZfub8TAUroTRFkl3SIe5HTi/cMPP9CyZUu7bRs3bmTy5MkOE+/bt29z7dq1tMYnkqMlN/3Mn0LMZB/bcLOewoy98OI2y+9vtYYX/qtcap3Cbk3uE7P275zFfmawlzjMSaa9i0j20bx5cyXYIh5kXUpmbQ3qdLHUNHYjsYrHTEkKaQwX8TBNNRfxoOSmn3Xia/cv+sF+GLPZ8vtrLWDif39wj6A+LxEMWHqEOqqsCpY/EqbSjudobDftXUSytqioKPLnz0/evHk9HYqIJGB9qL2Xc861B01jN5KENGNNJGtwq7iaiKQP6/SzdDPnAPzfRsvvEx+0JN4JzOUQn3CAcsygNQspz0zmcSjZywXiS0sqKOkWySaKFSvGu+++a7dt//79zJ4920MRiYjVBa4zhV3OTS9PYzcSKyMwmiC3zhWR9KXEW8SDElcyT1MKPu8QPPWd5ffng+DN1pCoR288Zt7mR9ugr2rlIjmL2WzGbLb/s37jxo2MHj3aQxGJCMAgVtOIz/kfF1M/OB26kRiwzHIDA9PYk+qDdhHJeEq8RTxsCPU4wyhCGchaHkv2OP+U+m4uDIdh6yy/P9cY3mubJOlOjrVauYiIiKS/MCJYyM/OHexkN5KUGIF3actcDjlsYSYinqHEW8RDIjCxnF9Yzi8AtKQCl4hO9vhL3HS8Y8kRGPwtmIGnG1gGaieTbrD8R0Brv0RERDLGj5x17sAUupE4w4iB52nKn4ymAWUc1pDRg3YRz3GpuNr69eu5ePG/KTIHDhwA4Omnn05ybFhYWBpDE8m5pv7bJszKgOXp9Itsde1CK36F/qstSfewevDBwy4l3QDv0FZruEVERDLIaa6lflDCbiRvtrLrRuKM52nKczS2G88TV09XkTURz3Ip8T5w4IAt2U5ozpw5Do83uJgAiOQG0xIl3WDJm8e72q979VF4bBXEm2FwHZjT0dLj00lGDLxLCM/j2uAuIiIiKYvAxHEiWczPzCc85YM//Mm+G8lLwU7fpy4BrOWxJA/QE7cwU1tQEc9zOvEODQ3NyDhEcoUITEmSbiszljffTiXf6/+A3ishzgz9asFnnZxOup+lEd2ophZhIjnUl19+yb59+2yfT5w4AcDDDz/s8HiDwcB3332XKbGJ5AbzOMSTrHOuV/enB+DZ7y2/O+hGkprDXEp2n7WFmdqCimQNTifeLVq49h8CEUnqOJEpDsNOJd0bT0D35RAbD31qwPwu4OVcuYYePMBsHP/xLSI5w4kTJ2zJdkIbN250eLxmp4mknwhMzifd8w7BiJS7kaTGum47uaQ6EF8l3CJZhEtTzUUkbQrjnbYLbD0Fjy6FO3HQvRos7gp5kk+6e/AA42jKbs7RjLI0JDBt9xeRLO306dOeDsEt9957L3/++afdtilTpvDiiy/aPh8+fJhnnnmGsLAwSpYsybPPPsu4ceMyO1SRFB0n0rmke9HPbncjSUjrtkWyDyXeIhnIusarMn5s4iRDWev+xX44A52/hpg46FIFvu6eYtLdj5ospjuAEm6RXKJ8+fKeDsFtkydPZtiwYbbPRYoUsf0eFRVFu3btCAkJYc6cORw5coQnnniCokWL8uSTT3oiXBGbhGO9Uw/Y09CNxHqUGbRuWySbUeItkkESrvFyeu12cn78Ex5ZArfuwsOVYVkP8PZK8ZQphKTljiIimapIkSIEBAQ43PfVV19x584dvvjiC/LmzUv16tUJDw9n+vTpSrzFoxKO9UYM9OCBlE+wdiOJN7vcjcQI7GMopSmiddsi2ZD6eItkgMRrvNKUdO89Bw8vgZux0K4irOoF+VJ+ZtaGChqMRSRbeeeddyhevDh169Zl6tSp3L1717Zv7969BAcHkzdvXtu29u3b8/vvv/PPP/84vF5MTAxRUVF2PyLpKfFYH4+Z5fya/Alp7EYSD0QTSyC+tNQ4L5Lt6I23SAZweo1Xan76Cx76Cm7cgdYVYE1vyJ/6/9tOoU3a7y0ikkn+7//+j3r16uHn58eePXuYMGECFy5cYPr06QBcvHiRChUq2J3j7+9v21esWLEk15wyZQqTJk3K+OAl13JprE9DNxIrrecWyd70xlskA1TGDyNprBR86AK0/xKiYiC4PKztAwVSXzvWgwe0pltEPO7FF1/EYDCk+HPs2DEAxowZQ8uWLalVqxYjRozg/fff54MPPiAmJsbt+0+YMAGTyWT7OXfuXHp9NRHAhbE+Dd1IrLSeWyT70xtvERckLKASiG+SzwBhRPAjZ+lAJb7juHs3+vkitF0M125Ds7Lw3eNQKG+qpz1LI7ULE5EsYezYsQwaNCjFY+677z6H2xs3bszdu3c5c+YMVapUISAggEuX7PsVWz8nty48X7585MuXz/XARZwUiC/9qcVCfk7+oMTdSBY9mmJh1MQ+4WGqUlLruUVyACXeIk5KXEClP7VYzGHb57l04kf+THkAdsYvlyFkMUTegsb3wIa+UDj1pPs92vICzdJ2bxGRdFKyZElKlizp1rnh4eEYjUZKlSoFQFBQEC+99BKxsbF4e1tm/mzZsoUqVao4nGYukhnCiEh5zE/YjaRzFVjSPdXCqAkZgI5UUcItkkM4lXgn90Q6NQaDgZMnT7p1rkhW4qiASsLBNh6z3X63Hf0b2iyCKzehQRnY2A98Un5js5weBFFWA7OIZEt79+5l//79tGrViiJFirB3715Gjx5Nv379bEn1448/zqRJkxgyZAjjx4/nl19+YdasWcyYMcPD0UtuZX0Yn6zE3UiW94C8riXdn9FZY7tIDuJU4h0fH48hUauDO3fucOHCBctF8uShePHiXL161VaFtHTp0nbVR0WyM2cKqKQ56f7jKrReBJejoU4AbOoHRfOneIoBlHSLSLaWL18+li5dyuuvv05MTAwVKlRg9OjRjBkzxnaMr68vmzdv5plnnqF+/fqUKFGCV199Va3ExCMSP4xPwo1uJFb9qUUn7tfYLpIDOfVfgTNnzth9vnbtGiEhIVSuXJm33nqLoKAgjEYj8fHx7Nnz/+3deVxU1fvA8c+AAiKbC664a5ZpbinhgrjiRmpumbnvaa65lWnaouWWWWbumn3V0p+aSynu5r6R5paaiJhoioLigjDn98c0E8MMMDMMDODzfr14xdx77p3nzpDnPveee56DTJgwgbi4OHbs2JERMQuR6fQTqKSWXDuhK/VhkyvR0Gg5RD2EKoUgtBvkz5PmZgq4TLR0zkIIevfubdN2Go2GxYsX2zkay9WoUYPDhw+n2e6VV15h//79mRCREKk7yPWUzwdsrEaiF8ILdKSynSIVQmQlNj3jPXbsWJ48ecKRI0dwdv5v2IyTkxP16tVjx44dVK1albFjxzJ//ny7BSuEo/jhzQJCGMAmEv99pjt5p2su6W5FBbZyKfV74eH3dXe6bzyASr6wozsUdLcoLg1IaREhBADLli0zu1yj0aCU6b9C+uWOTryFyGrMTZyqt5iT9OVn8xvaWI1ECPF8sKmc2MaNG2ndurVR0p1Urly5aN26NRs3bkxXcEJkJX2oQTjD+ZEOKAuGlfeiGnXwowgeKTe6HgMNl0NEDLxQAHZ2h0J5LY5pPPXlbrcQAoCrV68a/Vy5coXWrVtToEABPv74Y/bs2cP58+fZs2cPU6ZMoUCBAoSEhHDpko3VF4TIgRZzklJ8SSOWU4ovWcxJQJeM/8gfKSfdNlYjSUr/+JgQImey6Y53bGwsMTExqbbR180UIifxw5uCRFv0NPdSwlJvcCNWl3SH34dy+WBXdyhiPknXgMl7dqQSn9LYgkiEEM+DUqVKGb2eNm0aR44c4ffff6do0aKG5RUrViQwMJBevXpRvXp11q5dy5gxYzI7XCGyHHMTqfbnZ+7xmLHsSHl4uY3VSJLSoKtOcoloALmoLkQOZNMd75dffpnVq1enOGP5pUuXWL16NZUryzMqIuepQH40aTdLXdRD3fDyK/egjA/s7gHFvVJs3p2qXGcE39KSSQRylL78SKf0RiGEyMEWL15Mp06djJLupIoXL06nTp1YuHBhJkcmRNZkbiJVLTCG0JST7gt3rK5Gkty3tORzmjKWHSZ32oUQOYdNifeECROIiYmhevXqjBgxgnXr1rF//37WrVvH8OHDqVmzJg8ePGDChAn2jtdm33zzDaVLl8bNzQ1/f3+OHj3q6JDE8+p2nG4itT/vQklv2NUDSqR+ZXslpwEYSG0+ohG18MuMSIUQ2VhkZCRubqlXRnBzcyMyMjKTIhIia0vpwnqKo9wu3dX151ZUI0nuC5rSmoqMS3JHXYtiAJuIREaOCpGT2JR4t2nThmXLlqHRaJgzZw6dOnUiKCiITp068dVXX+Hk5MTSpUt5/fXX7R2vTdasWcPIkSOZNGkSJ0+epGrVqgQHB3P79m1HhyayoUsWDjU3684jaLICzt+B4p664eWlfdLcLBHF5X+HnwkhhCX8/PxYv349T548Mbv+0aNHrF+/Hj8/uZAnBOiGd4+ijmWNr0TrHhe7aV01kqQGUpPR1DV7p136fSFyHpsSb4Du3bsTGRnJ8uXLGTFiBL1792bEiBEsX76ciIgIunfvbs8402XWrFn069ePXr16UalSJebPn4+7uztLlixxdGgiG9KXFrNa9GPdxCtnbkNRD93w8nKWz0h+nL+tf08hxHOrb9++/PXXX9StW5eNGzdy9+5dAO7evcuGDRuoV68e4eHh9OvXz8GRCpF1dKJS2j18OqqR6GmADwgEzJ9XOKORqiVC5DAaZa7GSA4SHx+Pu7s7a9eupW3btoblPXr04P79+2ZnXn/69ClPnz41vI6NjaVEiRLExMTg5ZXyc7ji+bGYk4bSYha5/0R3p/vETd2s5Xt7wosFrXpPZzSEM1wmXBEiB4iNjcXb2ztD+xWtVku/fv1YunQpGo3upN7JyQmtVlf8UClFr169WLRokWF9TpYZn7nI3hZz0mhyNbOux0CDZXD1vq4ayd6eKU6Mmpr3qMMw/A19etLzCmc0fEcIfahh03EIITKPNX2LTbOaJ/Xw4UP+/PNP4uLiqF+/fnp3Z3d37twhMTGRwoULGy0vXLgwFy5cMLvN1KlTmTx5cmaEJ7IBc/U8+1CDaB4zhtC0dxD7FJqv1CXdBd11w8utTLrhv2FnkngLISzh5OTE4sWL6d69O8uXL+f06dPExMTg7e1N1apV6datG0FBQY4OU4gsIfmM5mbpq5FcvZ9mNRJzNIA/xTnCDWZwkFkcYsG/CXYfahBMOS4TTXkz9cOFENmfzYl3eHg4w4YNY+vWrWi1WjQaDQkJCQAcOHCAfv36MW/evGzZqY8fP56RI0caXuvveIvnT9Kr3xpgFHXoRCWO87dlSffDeGjxAxy5oXv2a0c3eLmQTbHIsDMhhC0aNGhAgwYNHB2GEA5l7iJ6UuaeszZiZTWSpJzQsJr2lMaH11hseBf9JGrBlMMPb8OPECJnsinxjoiI4LXXXuPu3bu0adOGqKgoDh06ZFjv7+/PnTt3WLVqlcMT74IFC+Ls7MytW7eMlt+6dYsiRYqY3cbV1RVXV+tKQYicJ/nVbwXM4CAzOGjZDuLiodX/4OB13Synod2gqvm/uZTo63frh51JhyyEEEJYJ+lFdCc0hrvMScURn/IObKhGoqcBFhBCRyqzm6spTqIm/bsQOZ9Nk6tNmjSJe/fusXfvXtauXUvTpk2N1ufKlYv69etz4MABuwSZHi4uLtSsWZOdO3calmm1Wnbu3ElAQIADIxNZ3UGup371OzWPnsHrq2HfNV09z+1vQw3ztXRT4oyGI/RlNz0IZ7g86yWEsFpCQgKzZ8+mdu3aeHl5kSvXf9fbw8LCeOedd/jzzz8dGKEQGSv5RfSUSnX9yV3zO7CxGglAAH5EMMLQf8skakI832xKvLdt20a7du2oUyflkgulSpXixo0bNgdmTyNHjmThwoUsX76c8+fPM2jQIOLi4ujVq5ejQxNZ1GJO8iZrbdv4SQK0WwO7roKHC/zaFWoVt3o302hCLfwIooxcCRdCWO3x48c0bNiQ9957j2vXruHl5UXS+VTLlCnD0qVLWbFihQOjFCJjpVWqK5IYdnOVLZi5AJXOaiRzaG7Uf/vhzQJCcP43+ZbRbEI8X2xKvKOjoyldunSqbZRSRjODO1Lnzp2ZMWMGEydOpFq1aoSFhfHrr7+aTLgmBPx3ddyme91PE6D9j7D9Crjnhq1vQYBt8wO8SjGbthNCCIDPPvuMAwcOMHXqVKKioujbt6/Rem9vbxo0aMC2bdscFKEQGS+1u8yLOUkpvqQRy9lFuPGG959As+8hLEpXjWRXD6hQwOL37UFVauFnsrwPNQhnuIxmE+I5ZNMz3oULF+bSpUuptjlz5gwlS5a0KaiMMGTIEIYMGeLoMEQ2kOYEKymJT4ROa2HrJciTC7a8BfVL2RSDDD0TQqTXmjVraNiwIWPGjAEwWzKsbNmynDp1KrNDEyLT6O8y60t1OQEjCOAmD1KexTyd1Ui+pSUDqZ1qTHKXW4jnj013vJs2bcrmzZs5ffq02fX79+9n165dtGzZMl3BCeEI5q6Op+lZInRZBz9fBFdn+LkLBJW2OYZpNJFOWQiRLhEREbz66quptvH09CQmJibVNkJkd/q7zAOpaZgo1Z9F5pNuO1QjaU1F+wQuhMhRbEq8J0yYQJ48eQgMDOTTTz/l8uXLAPzyyy98+OGHNG/enIIFCzJ69Gi7BitEZvDDm2k0sXyDBC10Ww//dx5cnGHDm9CkbJqbaf79MUeGmQsh0svT05Pbt2+n2ubKlSv4+vpmUkRCOM4q/mA+JwypttlxbXaoRvIFTeXCuRDCLJuGmpcuXZpt27bx5ptv8uGHH6LRaFBK0bp1a5RSlCxZkrVr11K0qHWzOAuRVdwmzrKGiVrotRHWnIXcTrCuEzQvb9GmCt1wtHfYanQCIMPMhRD28Nprr7Fp0ybu37+Pj4+Pyfrr16+zdetW2rVrl/nBCZGJIolhLKGpN3qc/mok02nKe9RNR6RCiJzMpsQbdLW6L126xKZNmzhy5AjR0dF4eXnh7+9PmzZtcHFxsWecQmSaSGKYxaG0G2oV9N0EK09DLif4sSO0fsHi93FGQ2sqkptchmfPZIZTIYS9jB49moYNG9K4cWO++uorEhISAHj06BGHDh3i3XffJSEhgZEjRzo4UiEy1iWiU5+55UkCtLW9GokGOEJfs5OpCSGEns2JN+jqdbdr106uloscIZIYLhHNP8SlPbmaVsHAzbAsDJw18L83oO2LqW7Sg6qs5LRJgt2HGgRTjstEU578knQLIewiMDCQr7/+mmHDhhEYGGhY7unpCYCzszPz5s2jZs2ajgpRiEzhQe6UV9qhGsko6kjSLYRIk02Jd6NGjejZsyfdu3dPsc3KlStZsmQJu3btsjk4ITLLYk7Sj58N6baGFJ7/AlAK3t0KC0+Ckwa+bwcdX051/5voQmsq8gmNzCbYMsOpECIjDBo0iKCgIObPn28yOu2dd97h5ZdT/7dLiJzgOH+bX2GHaiTOaBiGvx2iFELkdDYl3nv27CEoKCjVNteuXWPv3r227F6ITHWMSPrys9GyVJPuEdtg3nFddr60DXSpkur+G1DKMMOpJNhCiMwSERGBj48PL730EnPmzDHb5sGDB9y7dy9Llf8Uwp5mcIAx5p7vfpYIb9lWjcQJDVp5PEwIYSWbZjW3RFxcHLlzpzK0R4gsYDEn8WeRZY2VgjGhMOeI7vWi16F71TQ3W8kb6YhQCCFsU6ZMmRQTbr2vvvqKMmXKZFJEQmSu6RxgNKGmF9P11UjWWVeN5D+KH+lAOMPpQw07RiyEyMksvuMdERFh9Pr+/fsmywASExO5fv0669ato3Tp0ukOUIiMEkkM/dmU1tPcOkrBB7tgxr+Trs1vBb2rp7mZlBURQjiKUgqlUv8XLq31QmRXKc5kno5qJHpawJe80r8LIaxiceJdunRpNBpd1WGNRsOcOXNSvZKulGL69Onpj1CIDHKJ6LQnUdObvBem/qb7fW4LGPCqRZvVknrcQogsLDIy0jDZmhA5ySfsM+3hk1YjcdbAmg5pViPJhYaEZHuSsp9CCFtYnHh3797dUK97xYoVVK1alWrVqpm0c3Z2Jn/+/DRq1IjmzZvbM1Yh7KoC+VOfRE3v0326xBtgVjMYUtui/TtJxyyEyGRTpkwxer1nzx6z7fSj01avXs1rr72WCZEJkXkmsJPvOGG8MHk1klXtod1Lqe7HlzycZCDbuCJlP4UQ6aZRNowzK1OmDCNGjGDo0KEZEVOWExsbi7e3NzExMXh5eTk6HGElfZmwCslmEo8khpLMTj3x/uIAjN2h+/3zJjCmrsXvO52mvIfl7YUQz4+M6lecnP6bukV/sTw1xYoVY/369dSqVctuMWRV0pfnXMeIZD8R1KckG7nIp+w3bqAUDNmqmxhVX43krdQnRtXTAAt5Xcp+CiHMsqZvsWlW86tXr9oUmBCZIWmivY0r9GcTWhROaFhAiGEilEtEp550zz70X9L9cUOrku4vJOkWQjjA7t27Ad3jXvrSnz169DBppx+d9uKLLxol60JkNz1Zz3J+T7mBuWokFibdoBsVN4BNhDOcIGQiQiGE7WxKvM+dO8eOHTvo0qULvr6+Jutv377N6tWradq0KS+9lPowHiHsaTEnDYm25t9l+uRai2IAm3iFQjzkGR6kMuv+10dh5Hbd7xMDYUKgxTH8SAc6Utmm+IUQIj0aNGhg+H3SpEkEBQUZLRMiJzlGZNpJtw3VSJJLRHGZaLnTLYRIF5sS72nTprFz506GDBlidn2BAgWYPn06p06dYunSpekKUAhL6Wcp10+YZu5udiIKfxalfqf7u+Pw7i+638fXg4+CLI7BGQ0BlLC4vRBCZJRJkyY5OgQhMtR+TKvrGNhYjcQcmUxNCGEPNo0v279/P40bN05xeJqzszONGzdm37596QpOCGtYOkt5qi2WnIKBW3S/jwqATxuBRpPaFgYy4YoQIis5ePAgI0eOJCoqyuz6mzdvMnLkSA4fPpzJkQlhH/UpmfJKG6uRLKUN71HHcIIsfbsQwl5suuMdFRVFiRKp39UrXrw4N2/etCkoIWxRgfw4oTFKvpMPN0/Vit+h78+634f5w/SmaSbd71GHTlQijmcy4YoQIkuZOXMmp0+fZtasWWbXFy1alM2bN3Pjxg3WrFmTydEJkX5F8cSf4hzhhvEKG6uR9KAqPdHdFR+Gv0ymJoSwK5sS77x583L79u1U29y+fRs3NzebghLCFn54s4AQo5IfU2nCWELT3njVGei1UZehD3oVZgenmXR/S0sGYllnLoQQme3YsWM0btw41TaBgYGEhlrwb6QQDpa8QknSOV2MfHEAJugmGeTzJjAiIM19B1KCGQRTCz/DMj+8JeEWQtiVTYl3jRo12LBhA9OnT8fHx8dk/b1791i/fj01atRIb3xCWKUPNYxKfqQ5cznAT2eh23pdjc++1eHrlmkm3RqgNRXtFbYQQtjd7du3KV68eKptihQpkuaFdCEcLWmS7YSGaTRhHDtMk24bq5F0oYpR0i2EEBnBpme8Bw8ezN27d2nYsKHJc9x79+6lYcOG3Lt3L8XJ14TISH54E0QZ/PBOfeZygA0X4K3/g0QFPavBdyFonNJ+pnsUdeRKuBAiS/Px8SEiIpXJp4Br167h4eGRSREJYb3kE6dqUYwj1DTp/sb2aiRyIV0IkRlsSrzbtGnDiBEj+P3332nYsCHu7u6ULVsWd3d3GjVqxOnTp3nvvfdo27atncMVwjo/ci7llZv/hE4/QYIWulaBRSFgQdLthO7ZLyGEyMpee+011q9fz/Xr182uj4iIYMOGDdSpUyeTIxPCcuYmTtUmb7TgBAyxrRrJIl6XC+lCiExhU+INuklbfv75Z4KDg8mbNy+RkZF4eHjQokULtmzZwueff27POIWwyDEimcVBjhFJJDHM4KD5hr9ehvY/wjMtdH4ZlrUFZ93/DmkNTR8pd7uFENnAyJEjefToEXXr1mXFihWGCU9v3rzJ8uXLqVu3Lo8fP2bUqFEOjlSIlFUgP6leEl9yCgZs1v1uZTWSTXShD/JYpBAic9j0jLde69atad26tb1iEcJiSSdZAd0V8W85xk9J7nD74Wl+4x1/QdvVEJ8I7V+C79tBLsuuQcndbiFEdhEYGMisWbMYNWoUvXr1AkCj0aCU7vKik5MTc+bMITDQ8iG5QmQp31tfjUSvB1VliLkQIlOlK/EWwhGSTrKiIeU71JE8MF24JxxeXwVPE+H1ivC/9pDb2ahJSvuUWp5CiOxm2LBhNGzYkPnz53Ps2DFiYmLw8fGhdu3aDBw4kMqVKzs6RCFSleIkqavOQE/rqpEAtKUi71NfJlMTQmQ6SbxFtpJ8khWL6nPr/RYBrf8HjxOgZQX4sQO4OJs0609NvuOEyfJVtKcjcpIqhMheXnnlFebNm+foMISwidlJUm2oRqInSbcQwlEsGl/r5ORErly5+PPPPw2vnZ2d0/zJlUvyemFf5iZZscih69DiB4h7Bk3LwrpO4Gr69zmAmkwgEKdkT5Q5oyGAEraGLYQQQggrLeYk/iwyXmimGoklE6OCbni5JN1CCEexKDMODAxEo9Hg7u5u9FqIzHaCv63f6NgNaP4DPIyHhqVhw5vgZv5PvyDu+OHNAkIYwCYSUTLEXAiRLfTu3RuNRsNnn31G4cKF6d27t0XbaTQaFi9enMHRCWG5SGI4yHX68bPxpXYbq5HUwY8vaW6SdOvni/EgNw95RgXyS18vhMgwGqWfZUWkKDY2Fm9vb2JiYvDy8nJ0OM+tSGIoxZfW3fE+eRMar4D7TyCwFGx9C/K6pLrJFzRlNHWJJIbLRFNeOmIhhJ1lRL/i5OSERqPh/PnzvPDCCzg5WTZppEajITEx0S4xZGXSl2d9kcTwCftYwAnTnv7Xy9Dm34lRO78MK9+weGLUo/Q1SbqTzhej54SGBYTITOdCCItZ07fIWHCRbRzkunVJ9+lb0PR7XdJdpwRs7pJm0g0wjlC6UBk/vCXhFkJkG1evXgWgePHiRq+FyA4Wc5K+/Gx+ZdJqJG9YV40EII5nRq+Tzxejp0UxgE0EU076fyGE3UniLbIF/ZVpi529rbvTHf0YaheHX7qCp6tFm2qBy0RLpyuEyFZKlSqV6mshsqpIYlJOupNWIwl5AVaZViNJjTMayv9belQvtfliElFyDiCEyBAWJd6WPieWnDw3JiyVtC530s5O/5yXuSvTKbpwR5d033kENYvCtrfBy7KkG8x30kIIIYTIGAe5bn5F8mokP3U0W40kJSnN0VKB/DihMXteIecAQoiMYlHivWzZMrPLNRoN5h4R1y+XxFtYIulzVkmfr5rOAcYSat0c5pfuQqPlcCsOqhaG7d3Ax83izWUiNSGEECJz7cLMYxEWViMB0ABH6Es49wEojQ9xPEtxjpbkk6jqyTmAECIjWZR4J39OTKvVMmzYMA4fPsywYcOoX78+hQsX5tatW+zbt4+vvvqKgIAAZs+enSFBi5wj+XNW+uerrnKPT9lv3c7+ugeNVsDNh1C5EOzoDvnzWLSpMxpW0Z4ASkiHK4TIlmR0msiOIonhO04YL7SiGgnAYGpTCz+rSoX1oQbBlOMy0eQld6qJuhBC2INFiXfy58SmTZvGkSNH+P333ylatKhhecWKFQkMDKRXr15Ur16dtWvXMmbMGPtGLHKUORwxGeqViLI46e7AS6zlPITfh4bLITIWXioIO7tDQXeL40hE4Ute6XCFENmWjE4T2dEloo0XnLwJzVZC7FNdNZJNXcA9d6r7KEc+m95bJlEVQmQmy6eETGLx4sV06tTJKOlOqnjx4nTq1ImFCxemKziRs0USw0wOmiy3pkJ8cyrwzfV6uuHlETHwQgFd0l0or1WxyDNdQojs7urVq0Y/V65coXXr1hQoUICPP/6YPXv2cP78efbs2cOUKVMoUKAAISEhXLp0ydGhi+dIJDHs5iqRxAC6560NbKxGUpcSGRWuEELYjU2zmkdGRuLmlvpzs25ubkRGRtoUlHg+XCLa7PPbL1KQ89yxaB/9bqwkb6NVcPU+lMsHu7pDUc8U2zsB02hKfvIYnu2SZ7qEEDmBjE4TWV3yOV2m0YRXKca71Gbu2c02VSPpQVWrhpgLIYSjaJS58WdpqFChAkop/vjjD7MJ+KNHj6hSpQpOTk454kq6NYXRheUiiaEUX1pXmzupqIcQtAwu3oXSPrC3J5RMOXn+kQ5Gz3BHEsNlouWZLiFEpsuMfqVChQo0b96cuXPnpthmyJAhbNu2LUf01WmRvtyxUu3zL9zR9ee34nTVSHZ0T3Vi1CHUphz5qEsJSbqFEA5lTd9i01Dzvn378tdff1G3bl02btzI3bt3Abh79y4bNmygXr16hIeH069fP1t2L54T+llFnf8dXO5szSDz23G6K+MX70IJL9jdI9WkWwMmE6f54U0QZSTpFkLkSDI6TWQlKdbOtrIayQfUZy4tGU6AJN1CiGzFpjveWq2Wfv36sXTpUjQaXbLk5OSEVqsFQClFr169WLRokWF9diZXye1DX6vbg9xc/bfkR51/n8u6TDS3iaMza9Pe0Z1Huk76zG0o7qm7010u7eezd9ODIMqk4wiEEMI+MuuO9/M0Oi0t0pc7ltk73n/dgwbLdBOjVi6ku4ieysSoX9CU0dTN+GCFEMJC1vQtNj3j7eTkxOLFi+nevTvLly/n9OnTxMTE4O3tTdWqVenWrRtBQUG27FrkUEmf60pKAyzkdYIpx3n+SXtH0Y91E6+cuQ1FPGBXD4uSbieQydOEEM+Vvn37Mn78eOrWrcvEiROpV68eBQoU4O7du+zfv58pU6YQHh7O1KlTHR2qyKH0F9wr/PtIl1Ht7Gv3rapGcpS+codbCJGt2ZR46zVo0IAGDRrYKxaRQyWv1Z2UAvrys2U7uv8EgldCWJRu1vJd3XWzmFtgJHVkSLkQ4rkyevRo/vzzT5YuXcobb7wBmB+dNnr06AyN49NPP2XLli2EhYXh4uLC/fv3TdpEREQwaNAgdu/ejYeHBz169GDq1KnkyvXfacqePXsYOXIkZ8+epUSJEkyYMIGePXtmaOzCdsknUltACH2owT0eM/r6Wl3SbUE1EidgAa9L0i2EyPZsesY7q/j000+pU6cO7u7u+Pj4mG0TERFBq1atcHd3p1ChQowePZqEhITMDfQ5d5Drtk+gphf7FJqvhON/666I7+wOL/maNHPCtByZMxqG4Z++9xdCiGxGPzpt9+7d9OjRg+rVq1O6dGmqV69Oz5492bVrF4sXL87wR8Li4+Pp2LEjgwYNMrs+MTGRVq1aER8fz8GDB1m+fDnLli1j4sSJhjZXr16lVatWNGzYkLCwMIYPH07fvn3Ztm1bhsYubJP8grsWxQA2sZmLjL6xDhqtSLMayQfUZzc9uMYI+lAjk49ACCHsz+Y73gkJCcydO5dVq1Zx4cIFHj16ZEhow8LCWLBgAcOHD+eFF16wW7DJ6TvzgIAAFi9ebLJe35kXKVKEgwcPcvPmTbp3707u3Ln57LPPMiwu8R/9Fe90eRgPLX+AIzcgnxvs6KZ7FiwZDbqr4oCUChNCiH85enTa5MmTAVi2bJnZ9du3b+fcuXPs2LGDwoULU61aNT7++GPGjh3LRx99hIuLC/Pnz6dMmTLMnDkTgJdeeonffvuN2bNnExwcnFmHIixkbiK1RBQhUQt1E6NejtZVI9nVA4qbPhMpz3ILIXIim+54P378mIYNG/Lee+9x7do1vLy8SDpHW5kyZVi6dCkrVqywW6DmTJ48mREjRlClShWz6/Wd+cqVK6lWrRotWrTg448/5ptvviE+Pj5DYxOpDzG3WFw8tP4fHLgO3q4Q2g2qFjHbVAH7uUYfahDOcHbTg3CGy5VyIYTIwg4dOkSVKlUoXLiwYVlwcDCxsbGcPXvW0KZJkyZG2wUHB3Po0KEU9/v06VNiY2ONfkTmqEB+nJKPP7OwGkkIFSTpFkLkSDYl3p999hkHDhxg6tSpREVF0bdvX6P13t7eNGjQwOFDwCzpzM2Rzto+UiwdYqnHz+D11bD3Gni56kqM1CyW6ibL+Z1jREqpMCGEQDc6bfbs2dSuXRsvLy+jZ6bDwsJ45513+PPPPx0YIURFRRn104DhdVRUVKptYmNjefz4sdn9Tp06FW9vb8NPiRIlMiB6YU7ycqHceQRNVsC5f3TVSHb30N3xNmMLl4kkJvOCFUKITGJT4r1mzRoaNmzImDFj0Gg0Zp8PK1u2LBEREekOMD0s6czNkc46fSKJYTdXiSPemsrcxp4kQNs1sOsqeLjAL12hdnGLNj3AdVvfVQghcoyMHJ02btw4Q/+f0s+FCxfseThWGz9+PDExMYaf69elb8hMfajBIfpYXY1Ei+Iy0ZkYqRBCZA6bEu+IiAheffXVVNt4enoSE2P9Fcus0JlLZ21Kn0yndRV6MScpxZc0YjkhrLLtfvfTBOjwI2y/Au65YetbUMfyix91kQslQgiRkaPTRo0axfnz51P9KVu2rEX7KlKkCLdu3TJapn9dpEiRVNt4eXmRJ08es/t1dXXFy8vL6EdkrhX3j1pdjcQZjZT/FELkSDZNrubp6cnt27dTbXPlyhV8fU1nnU7LqFGj0iwPYk1nfvToUaNlyTtzc1xdXXF1dbXoPZ4HKZUESc4uz3Q/S4TOa2HLJciTCzZ3gfqlLN68B1Wl5IgQQmA8Og1IcXTaqVOnrN63r6+vTX28OQEBAXz66afcvn2bQoV0E2eGhobi5eVFpUqVDG22bt1qtF1oaCgBAQF2iUHYR9K63Q9iY/m6+dA0q5H0oCorOS0TogohcjybEu/XXnuNTZs2cf/+fbNlvK5fv87WrVtp166d1fvO7M5cpC6lkiDBlDPpGNP9THeCFrqsg40XwdUZNr4JDcukusl0mtKAUhzgOnUpIUm3EEL8KyIiIs1+2NbRadbGER0dTUREBImJiYSFhQFQvnx5PDw8aNasGZUqVaJbt2588cUXREVFMWHCBAYPHmy4CD5w4EC+/vprxowZQ+/evdm1axc//vgjW7ZsydDYheWSXqTXPIynWMufLapG8gmN+IRGXCaa8uSXpFsIkWPZNNR89OjR3Lt3j8aNG3PgwAFDGbFHjx6xc+dOgoODSUhIYOTIkXYNNrmIiAjCwsKMOvOwsDAePnwIYNSZ//7772zbts2kMxepS6kkiLnnr8zOYmqpBC10Ww/rzoOLM6zvDE3Lpdhcg67cyHvUpRZ+DCdAkm4hhEgiI0enWWPixIlUr16dSZMm8fDhQ6pXr0716tU5fvw4AM7OzmzevBlnZ2cCAgJ4++236d69O1OmTDHso0yZMmzZsoXQ0FCqVq3KzJkzWbRokZQSyyKMLtLHxaNa/48bB85aVI3kENdlQlQhxHPBpjvegYGBfP311wwbNozAwEDDck9PT0DXic6bN4+aNWvaJ8oUTJw4keXLlxteV69eHYDdu3cTFBRk6MwHDRpEQEAAefPmpUePHkaduUidPplOmnyn9PyVfhbTvvxs3ZskaqHXRlj9B+R2grUdoUUFs001wCjqMAx/6aCFECIVGTk6zRrLli1LsYa3XqlSpUyGkicXFBRk07B4kfEMF+ltqEbSmbXEEi+lP4UQOZ5NiTfAoEGDCAoKYv78+Rw5coTo6Gi8vLzw9/fnnXfe4eWXX7ZnnGbZqzMXKdMn0wPYRCIKJ2AqTVJMeu9hvqxLirQK+m2ClafBWQNrOkBIRbNNG1CKlbwhCbcQQlhg9OjRNGzYkMaNG/PVV18ZjU47dOgQ7777bqaMThM5XwXyo3mSgDJTjUQDaJJdwE9KQYqPsAkhRE5iU+K9b98+vLy8qFatGnPmzLF3TCKL6UMN7vGYsexAi2IcO8hPHsPV6WNEsp8IXqAAY9lh+Y61CgZthqVh4KSB/7WHdi+ZbTqE2sylpR2ORgghng9ZZXSayPl8n7pRpMMv3DRTjUQBa2iPL3nJS242c4kp7DXaXv8ImyTeQoiczKbEu2HDhgwYMIB58+bZOx6RBUQSw8F/a2HX+bc0lz7pBuMJ1kbwK2s5b/2bKAVDf4EFJ3Xjx79vB51MR0k4oeFzmvAedW0+HiGEeF5lhdFpImfSz2Be+pknIZ3f4OaWk+BmWo3EGQ0BlDAk1UXx5BP2WfQImxBC5CQ2Jd6FChXCzc3N3rGILGAxJ+nHz4buUP9MtbkJ1nqxgR1ctf5NlIKR2+CbY7o3WNoG3qpieL81dKA0PsTxTGY4FUKIdHrppZdkdJqwK8MM5gmJ8NY62HhOV43kZ+NqJBowKQ+W/BE2KSEmhHhe2JR4N23alD179qCUMlsXVGRPkcQYJd2gGyI2i0No/v09KZuT7rE74MsjutcLQ6BHNaP38yWvzFAuhBDp5OzszJtvvskPP/zg6FBEDmKYwTwhUVeNZO25FKuRaIBgTCuU9KEGwZSTEmJCiOeKTeXEpk2bxt27d+nfvz/R0aZlpUT2dIlos1OfaFG04oX0v4FSMGEXTD+oe/1tK+hjOotpXnKn/72EEOI55+XlRYkSJRwdhshhLhGNNjERev9bjSRXytVItGC2/CggJcSEEM8dm+54v/322/j4+LBkyRJWrlxJmTJlKFy4sMndb41Gw86dO+0SqMh4Fchv9s42wGb+TP8bTNkLn/2m+/2r5jDwVbPN4niW/vcSQojnXO3atfn9998dHYbIYdy1zrpqJN+nXY1Ent0WQoj/2JR479mzx/D706dPuXDhAhcuXDBpJ8PQsxc/vFnI6ybDze3is/3w0b+zmM5sBu/6m20mnbQQQtjHRx99RFBQECtWrKB79+6ODkfkAAu1x+k/aKBxNZI3zFcjkWe3hRDCmE2Jt1artXccIovQP3d1iOts4zKLCUv/TqcfgA926X6f1hhGBhhWNaE0uwhHi3TSQghhT6GhoQQFBdGrVy/mzp1LrVq1Uhyd9uGHHzooSpEV6Wcsr5Dk+evr6j79h74DC06kWY1kNe2NZjIXQggBGqWU3W9u5jSxsbF4e3sTExODl5eXo8PJFIs5SV9+Tv+OvjwMI7bpfp8SBB82MKxyQsM1hgPIBCtCiOdKZvQrTk6WTeOi0WhITEzMkBiykuexL7eFYcZyFE5oWEAIvVV1Oo7sw7ovl/5XjSTJxKh6+vZ9MJ2/RQghciJr+har7ngfOnSIDz74gGPHjqHRaPD39+eTTz7B39/8sGGRPelnLE23b47+l3R/GGiUdAMsSHJ3WxJuIYSwr927dzs6BJHNGGYs//eBMy2K/upnjo9drku6waQaCehy8QHU5AMCpT8XQogUWJx4nzlzhsaNG/PkyRPDsp07d3Lw4EGOHj3Kyy+bDjcS2UPyIWWXiDap2221BSdgyC+638fVhclBRqudMF9iRAghhH00aNAg7UZC/CuSGH7krHH/rxTaCbuYP103Merb345nVR9XEpOdIyhgISf5gMBMjFgIIbIXi8uJTZs2jSdPnvDBBx8QFRVFVFQUH374IY8fP+bzzz/PyBhFBlrMSUrxJY1YTim+ZDEnqUB+nEjHxHhLT8GAzbrfR74GnzWGZM8UplZiRAghhO0OHTpEo0aN8PT0xMvLi6ZNm3L06FFHhyWyMP25wCi2G69IUo3kq6++4vuBn3GIPmb3kYiSfl0IIVJh8TPeJUuWpHTp0uzbt89oeYMGDQgPD+fatWsZEmBWkJOeC0t6dxugFF8aXd12RkM4w9nGFdue8f7+d+ixQXf5e2ht+LK5SdKd9H1kSJoQ4nmUUf3KmTNn8Pf3NxqdBpAnT57nfnRaTurL7SmSGJNzAUBXjeTfiVFnzpzJyJEjAdjNVRqx3GQ/+nlbpF8XQjxPrOlbLL7jfevWLV577TWT5f7+/ty6dcv6KEWmS353ew5HTDraRBSbucgF7lj/Bqv/gJ4bdUn3oFdTTLoBRhAgnbMQQtiZjE4T1jL7eFmSaiTTpk0zJN1AiqPiPqeJ9OtCCJEKi5/xfvbsGR4eHibL8+bNy7Nnz+walLA/cxOmzOIgGjB5mnsQW61/g7Xn4O3/A62CvtXh65YpJt0aYBgyIZ8QQtjb/v37qVevHh9//LFh2eTJk9mzZw979+51YGQiq9In0obk+8vDMGYHAKOmvE/tsZ2IJMZoMtQFhDCATSSicAKm0ZT3qOugIxBCiOzB4jveInszd0Vbi2nSbZONF6DLOkhU0KMqfBcCTikn3Qt5Xa6KCyFEBpDRacJa+kTaGY1RNZLWH/Zl9ocuRnPA6PWhBuEMZzc9uMYIRkvSLYQQabKqnNjKlSs5fPiw0bLLly8D0LJlS5P2Go2GLVu2pCM8YS8mV7TtZcuf0PEnSNDCW1Vg8esmSbcGmEdLCuBOACUk6RZCiAwio9OELfpQgzsL9jPu32okg8eNYN5kL1SSUXID2EQw5YzufEt/LoQQlrMq8b58+bIh0U7u119/NVmmSWGosch8fnjzOU0YTaj9drrtMrzxIzzTQqeXYXlbcDYdRPEFTRlIbfu9rxBCCCHsZunSpYwbMByAfiMH88ZnQ/hGs8KojX7Wckm2hRDCNhYn3levXs3IOEQmuEWc/Xa28y9ouwbiE6Hdi7CyHeQy/+TCqxSz3/sKIYRIlYxOE9ZYuXIlffr8WyLs3dosmlGQCpqbJqPknNFQ/t+KKEIIIaxnceJdqlSpjIxDZIDkpcNmccg+O94bDiGr4EkChLwAqztAbmezTaWjFkKIzCWj04SlVq9eTY8ePVBKwcCaMKc5SgPj2cHnNGEcO0hE4YyG7wiRu91CCJEOVg01F9nHYk4aZjF3QsNIAuzzfPdvEdDqf/A4AVqUh586gkvKSbd01EIIkXlkdJqw1Nq1a3n77bfRarW6aiTftDJUI0lE8SrFCGc4l4mmPPmlLxdCiHSSxDsHMlc6bLY97nYfjoSWP0DcM2haFv6vM7ia/xNyAg7Rh1r4pf99hRBCWERGpwlLbNy4kS5dupCYmEiHHl1Y910FVJKJUfWj1WQCNSGEsB9JvHOAY0SynwheoAB5ceEf4kzubiem92738b8heCU8iIeGpWHDm+CW8p+PFohDZtAVQgghspItW7bQsWNHEhISeOutt1ixeAXLnH431OWW0WpCCJExJPHO5nqynuX8brTMCQ0ajGt0O6FLhm1y6iY0/R5in0L9krCpC7jnTnUTebZbCCGEyFq2bdvGG2+8wbNnz+jUqRPLly/H2dmZPtQgmHIyrFwIITKQJN7ZTNIJ027ywCTpBgzPdWtQaNElwcGUYyvmJ9tJ1elb0OR7uP8EAvxgy1uQ1yXVTeRquRBCCJG17Ny5k7Zt2xIfH0+7du1YuXIluXL9dxoow8qFECJjSeKdjSSfMK0DlVJsq0XxIx0AuMRdPmC39W947h9osgKiH0Pt4vBLV/B0NdvUGQ3TaMKrFJOr5UIIIUQWsnfvXkJCQnjy5AkhISGsXr2a3LlTH7kmhBDCviTxzibMTZi2lrOpbrOfCOZy1LY3vHAHGi2Hfx5BjaKw7W3wdjPbtBMvM5NmkmwLIYQQWcxvv/1Gq1atePz4MS1atOCnn37CxSX1kWtCCCHsz8nRAQjLXCLaZMI0LRBMuRS3sTnpvnRXl3TfioOqhSG0G/iYT7oB1nHOtvcRQgghRIY5fPgwLVu2JC4ujqZNm/J///d/uLqaH7kmhBAiY0ninU1UID9OaIyWOaNhEa+ziS7J1qTDX/eg0Qq4+RBe9tUl3fnzpLpJIorLRNsrAiGEEEKk0/HjxwkODubBgwc0bNiQbzYs55DbTSKJcXRoQgjxXJLEO5vww5sFhOD8b4rtjIYRBADQmoos5PX0J9/X7kPD5RAZCy8WhJ3dwTdvmpvJDOZCCCFE1nHq1CmaNm1KbGws9evXp8Omj3nRfQGNWE4pvmQxJx0dohBCPHck8c5G+lCDcIbzHnXQopjBQUoym+kc4BUKpa9Sd2SsLumOiIEK+WFXdyjsYdREA/xIB76gqdEFAJnBXAghhMgaTp8+TZMmTbh//z4BAQEs2PI/3s27w2iOmAFskjvfQgiRyWRytWxoFocMSbYCxhBKY0rbvsO/H+iS7qv3oWw+2NUDinoaNdEAC3mdjlQGoAuVpd6nEEIIkYWcO3eOJk2aEB0dTe3atfnll1846Wk6R4z+ETFL+++kpUylzxdCCNtI4p3NmJtkDWAn4bbtMOqhbiK1y9FQ2gd29wA/L0CXbA+gJo0oQwAljDpbqfcphBBCZB0XLlygUaNG/PPPP1SpUZUPfv2OB97/zRGT9NzBmkfEkpcyXUAIfaiRUYchhBA5lgw1z0YiieEf4uy3w3/ioPEKuHgXSnjphpeX/C+ZrksJviWEjlSWJFsIIYTIoi5dukSjRo24desWJaq+wB/bg2mTbwOl+JJtXDGZI8bSR8TMlTKVYepCCGEbueOdTSS94mwXdx9Bk+/h3D9QzFM3vLxMPqMmv3GdGRzgPera5z2FEEIIYVd//fUXjRo14ubNm7zw8ktcCm2NKqCrRqJPlMMZTjjDrX5EzNwoO2uHqQshhNCRO97ZQPIrzul27zE0/R5O34IiHro73eXNDzkbyw65si2EEEJkQdeuXaNRo0ZERkby4osv8tnOZShfd6M2SRPlIMpYlTCnVMpUKpkIIYT1JPHOBlJ6rtsmMU8geCWcigJfd13JsIoFU2yulRrdQgghRJYTGRlJo0aNuHbtGhUqVGDXrl34F65o10TZXClTqWQihBC2kaHm2UAF8qOB9KfesU+h+Q9w7G8okEc3vLySb6qbyJVtIYQQImv5+++/adiwIX/99Rdly5Zl165dFC1aFIAFhDCATSSi7JIo96EGwZSTSiZCCJFOknhnA354M4o6zOCg7Tt5GA+t/geHIyGfG+zoDpULGTVJntw7yZVtIYQQIku5desWjRo14vLly5QuXZrdu3fj5+dnWJ8RibJUMhFCiPSTxDub6EQlZnLQtrvej55ByCr4LQK8XSG0G1QrggY4Ql/CuQ9AACUAOMR1w2vpaIUQQois4Z9//qFRo0ZcvHiREiVKsGvXLkqWLGnSThJlIYTIeiTxzuIiiWEOR2xPuh8/g9dXwZ5w8HSBbW9DzWKA7u72aW6b1OPsKJ21EEIIkaXcvXuXJk2acO7cOYoVK8auXbsoU6aMo8MSQghhoWw7uVp4eDh9+vShTJky5MmTh3LlyjFp0iTi4+ON2p0+fZr69evj5uZGiRIl+OKLLxwUsfUWc5KSzGaGrUn3kwRotwZ2XoW8ueHXt8Hfz6iJ1OMUQgghsrZ79+7RtGlTTp8+TZEiRdi1axfly5d3dFhCCCGskG3veF+4cAGtVst3331H+fLl+eOPP+jXrx9xcXHMmDEDgNjYWJo1a0aTJk2YP38+Z86coXfv3vj4+NC/f38HH0HqjhFJP362fUK1+ETo8CNsuwLuuWFrV6hTwqSZ1OMUQgghsq6YmBiCg4M5deoUvr6+7Ny5k4oVKzo6LCGEEFbKtol38+bNad68ueF12bJluXjxIt9++60h8f7hhx+Ij49nyZIluLi48PLLLxMWFsasWbOydOK9mJP0Z5PtSfezROi8FrZcArdcsKkLBJYy21RmLRdCCCGyptjYWJo3b86xY8coUKAAu3btolKlSo4OSwghhA2y7VBzc2JiYsif/78k8tChQwQGBuLi4mJYFhwczMWLF7l3716K+3n69CmxsbFGP5klkhj6s8n2ut0JWnjr/2DDBXB1ho1vQqMyyap66jiBzFouhBBCZEEPHz6kVatWHD58mHz58rFjxw4qV67s6LCEEELYKMck3pcvX2bu3LkMGDDAsCwqKorChQsbtdO/joqKSnFfU6dOxdvb2/BTooTpEO2Mcolo25PuRC10Xw9rz4GLM/xfZ2hWDg3wBU1x/jf9dkbDe9ThGiNMJlYTQgghhGM9evSIkJAQfvvtN7y9vQkNDaVatWqODksIIUQ6ZLnEe9y4cWg0mlR/Lly4YLTNjRs3aN68OR07dqRfv37pjmH8+PHExMQYfq5fv57ufaYmkhh2c5VIYrj2b2kvqyVqoddGWPUH5HKCnzpCywo4AQt5nfeoSzjD2U0PwhnOdJrJnW4hhBAii3n8+DGvv/46e/bswdPTk23btlGzZk1HhyWEECKdstwz3qNGjaJnz56ptilbtqzh97///puGDRtSp04dFixYYNSuSJEi3Lp1y2iZ/nWRIkVS3L+rqyuurq5WRm4b/fPcWhQasO1et1ZB/03w/Wlw1sDq9vB6RT6jId2oZkiwpa6nEEIIkXU9efKEdu3asXPnTvLmzcsvv/yCv7+/o8MSQghhB1ku8fb19cXX19eitjdu3KBhw4bUrFmTpUuX4uRkfAM/ICCADz74gGfPnpE7d24AQkNDqVixIvny5bN77NZK/jy3TUm3UvDOFlgSBk4a+OENaF+JOvgxngb2DFcIIYQQGSQ+Pp4OHTqwbds23N3d2bp1K3Xr1nV0WEIIIewkyw01t9SNGzcICgqiZMmSzJgxg3/++YeoqCijZ7ffeustXFxc6NOnD2fPnmXNmjXMmTOHkSNHOjDy/6TreW7QJd3v/gLfnQANsKItL3QOZBNdOEBfu8UphBBCiIzz7NkzOnfuzJYtW3Bzc2PTpk0EBgY6OiwhhBB2lOXueFsqNDSUy5cvc/nyZfz8/IzWKaVLZr29vdm+fTuDBw+mZs2aFCxYkIkTJ2aZUmIVyI8TmjSTb7ND0JWCkdvgm2O6BkvaQNdXuMw9bhGXQRELIYQQwp4SEhJ466232LBhA66urmzcuJFGjRo5OiwhhBB2plH6LFWkKDY2Fm9vb2JiYvDy8rLrvqdzgDGEWreRUjBuB3xxUPd6YQj0/W92cmc0hDNcnucWQogsKiP7FWFeVvzMExMT6datG6tWrcLFxYX169fTsmVLR4clhBDCQtb0Ldl2qHlO8SrFrN9o4u7/ku55LY2SboBEFJeJtkN0QgghhMgIiYmJ9OrVi1WrVpErVy5++uknSbqFECIHk8TbwTzIbd0GU/bCJ/t1v89pDoNqmTRxRkN58tshOiGEEELYm1arpX///nz//fc4OzuzevVqXn/9dUeHJYQQIgNJ4u0g+trdV62p2z11P0zao/t9RlMYalpixBkN3xEiw8yFEEJkCZ9++il16tTB3d0dHx8fs200Go3Jz+rVq43a7Nmzhxo1auDq6kr58uVZtmxZxgefAZRSvPPOOyxZsgQnJyd++OEH2rdv7+iwhBBCZLBsO7ladpa8drdFZhyE93fpfp/aGEbVAXTzqo2iDp2oRBzPKE9+SbqFEEJkGfHx8XTs2JGAgAAWL16cYrulS5fSvHlzw+ukSfrVq1dp1aoVAwcO5IcffmDnzp307duXokWLEhwcnJHh25VSiqFDh/Ldd9+h0WhYsWIFnTt3dnRYQgghMoEk3pnM0trdRjOZzzkMo/+dgG1yEIyrB8AAajKBQEm0hRBCZFmTJ08GSPMOtY+PD0WKFDG7bv78+ZQpU4aZM2cC8NJLL/Hbb78xe/bsbJN4K6UYNWoUX3/9NRqNhiVLltC1a1dHhyWEECKTyFDzTJZS7W4n4Fta8iMduM4ImlFOt2LeMRi+Tff7hPowsQFOaDhKX+bLkHIhhBA5xODBgylYsCC1a9dmyZIlJC26cujQIZo0aWLUPjg4mEOHDqW4v6dPnxIbG2v04yhKKcaNG8fs2bMBWLBgAT179nRYPEIIITKf3PHORJHE8A9xZutya4EX8SWIMkQSwzauwMITMHirrsHYujClIU7AAkKohR9CCCFETjBlyhQaNWqEu7s727dv55133uHhw4cMHToUgKioKAoXLmy0TeHChYmNjeXx48fkyZPHZJ9Tp0413G13tIkTJ/LFF18AMG/ePPr27evgiIQQQmQ2SbwzSVrPdSedifwg12FZGAzYrFs54jWY2pgQTUXm0UrucgshhHCocePG8fnnn6fa5vz587z44osW7e/DDz80/F69enXi4uKYPn26IfG2xfjx4xk5cqThdWxsLCVKlLB5f7aaMmUKn3zyCQBz5sxh0KBBmR6DEEIIx5PEOxOYe65bn3wrTGci379yE/TeqFs5pBbMbAYaDd14RZJuIYQQDjdq1Kg0h0qXLVvW5v37+/vz8ccf8/TpU1xdXSlSpAi3bt0yanPr1i28vLzM3u0GcHV1xdXV1eYY7GHq1KlMmjQJgBkzZqTrQoIQQojsTRLvTGDuuW4F/EgHfMlrNBP5mjVrmNdjgq7BgJrwVQvQaHBCQwCZf6VeCCGESM7X1xdfX98M239YWBj58uUzJM4BAQFs3brVqE1oaCgBAQEZFkN6zZgxg/fffx+Azz77jFGjRjk4IiGEEI4kiXcmqEB+nNAYJd/O/ybSSe9gr1u3jq5du6LVaqnXpw0H51VFq9FIbW4hhBDZVkREBNHR0URERJCYmEhYWBgA5cuXx8PDg02bNnHr1i1ee+013NzcCA0N5bPPPuO9994z7GPgwIF8/fXXjBkzht69e7Nr1y5+/PFHtmzZ4qCjSt2cOXMYPXo0oJvVffz48Q6OSAghhKNJ4p0J/PBmASEMYBOJKLOJ9MaNG3nzzTdJTEyke/fuLF2wlL+dHnCZaKnNLYQQItuaOHEiy5cvN7yuXr06ALt37yYoKIjcuXPzzTffMGLECJRSlC9fnlmzZtGvXz/DNmXKlGHLli2MGDGCOXPm4Ofnx6JFi7JkKbF58+YxfPhwACZMmMDEiRMdG5AQQogsQaOS1usQZsXGxuLt7U1MTAxeXl427yeSGLOJ9NatW2nbti3Pnj2jS5cufP/99zg7O9sjdCGEEFmQvfoVYbnM+MwXLlxI//79ARgzZgzTpk1DozE3paoQQoicwJq+Re54ZyI/vE3uXG/fvp033niDZ8+e0bFjR1asWCFJtxBCCJHNLFu2jAEDBgAwYsQISbqFEEIYcXJ0AM+znTt30qZNG54+fUrbtm354YcfyJVLroUIIYQQ2cnKlSvp3bs3SimGDBnCzJkzJekWQghhRBJvB9m7dy8hISE8efKE1q1bs2bNGnLnzu3osIQQQghhhTVr1tCjRw+UUgwYMICvvvpKkm4hhBAmJPF2gAMHDtCqVSseP35MUPMmDFk7ndsujx0dlhBCCCGskLQaSZ8+fZg3b54k3UIIIcySxDuTHTlyhBYtWhAXF8dLTfzZ+3/+NHddTSm+ZDEnAd0kbLu5SiQxDo5WCCGEEMlFEsMnPy80qkayYMECnJzktEoIIYR58kBxJjp+/DjBwcE8ePCAgKB6HN4YiMqj+wq0KAawiWgeM44daFE4oWEBIfShhoMjF0IIIQTAYk7Sb+tMVIfVkKCldpdglixZIkm3EEKIVEkvkUnOnj1Ls2bNiImJoV69ekzY9C3K3fiZ7kQUYwlFi67Cmz4ZlzvfQgghhONFEkO/3V+h3lgDz7TQsRLHV9TmpvNDR4cmhBAii5M73pmkRIkSVKpUCa1Wy9atW4nx0OKExpBkAyavQZeMXybapAyZEEIIITLXJaJRFQtAmXzwYkH44Q20uZyknxZCCJEmSbwziZeXF7/++iuJiYl4enriCSwghAFsIhGFMxqm0YSx/w4z13NGQ3nyOy5wIYQQQgBQgfw4FfNCu68neLtBbmfpp4UQQlhEEu9M5OHhYfS6DzUIphyXiaY8+fHDm3zkMUrGvyNErqILIYQQWYAf3rqL5r7STwshhLCOJN4O5oe3UYdtLhkXQgghRNYg/bQQQghbSOKdBSVPxoUQQgiRdUg/LYQQwloyq7kQQgghhBBCCJGBJPEWQgghhBBCCCEykCTeQgghhBBCCCFEBpLEWwghhBBCCCGEyECSeAshhBBCCCGEEBlIEm8hhBBCCCGEECIDSeIthBBCCCGEEEJkIEm8hRBCCCGEEEKIDCSJtxBCCCGEEEIIkYEk8RZCCCGEEEIIITKQJN5CCCGEEEIIIUQGksRbCCGEEEIIIYTIQJJ4CyGEEEIIIYQQGSiXowPIDpRSAMTGxjo4EiGEEDmBvj/R9y8i40lfLoQQwt6s6c8l8bbAgwcPAChRooSDIxFCCJGTPHjwAG9vb0eH8VyQvlwIIURGsaQ/1yi53J4mrVbL33//jaenJxqNxtHhGMTGxlKiRAmuX7+Ol5eXo8Oxi5x4TJAzjysnHhPkzOOSY8p6lFI8ePCAYsWK4eQkT31lhqzUl2f3v9/0eJ6PHeT45fif3+PPqcduTX8ud7wt4OTkhJ+fn6PDSJGXl1eO+gOGnHlMkDOPKyceE+TM45JjylrkTnfmyop9eXb++02v5/nYQY5fjv/5Pf6ceOyW9udymV0IIYQQQgghhMhAkngLIYQQQgghhBAZSBLvbMzV1ZVJkybh6urq6FDsJiceE+TM48qJxwQ587jkmITIWp7nv9/n+dhBjl+O//k9/uf52PVkcjUhhBBCCCGEECIDyR1vIYQQQgghhBAiA0niLYQQQgghhBBCZCBJvIUQQgghhBBCiAwkibcQQgghhBBCCJGBJPHOhsLDw+nTpw9lypQhT548lCtXjkmTJhEfH2/U7vTp09SvXx83NzdKlCjBF1984aCILfPpp59Sp04d3N3d8fHxMdsmIiKCVq1a4e7uTqFChRg9ejQJCQmZG6iVvvnmG0qXLo2bmxv+/v4cPXrU0SFZZd++fYSEhFCsWDE0Gg0bNmwwWq+UYuLEiRQtWpQ8efLQpEkTLl265JhgLTR16lRq1aqFp6cnhQoVom3btly8eNGozZMnTxg8eDAFChTAw8OD9u3bc+vWLQdFnLZvv/2WV155BS8vL7y8vAgICOCXX34xrM9ux2POtGnT0Gg0DB8+3LAsJxyXyLks6dc0Go3Jz+rVq43a7Nmzhxo1auDq6kr58uVZtmxZxgdvB/bq17Pr8SdXunRpk+962rRpRm2y27mbNbL7+ZClPvroI5Pv+cUXXzSsz2n9lj3OE6Ojo+natSteXl74+PjQp08fHj58mIlHkTkk8c6GLly4gFar5bvvvuPs2bPMnj2b+fPn8/777xvaxMbG0qxZM0qVKsWJEyeYPn06H330EQsWLHBg5KmLj4+nY8eODBo0yOz6xMREWrVqRXx8PAcPHmT58uUsW7aMiRMnZnKklluzZg0jR45k0qRJnDx5kqpVqxIcHMzt27cdHZrF4uLiqFq1Kt98843Z9V988QVfffUV8+fP58iRI+TNm5fg4GCePHmSyZFabu/evQwePJjDhw8TGhrKs2fPaNasGXFxcYY2I0aMYNOmTfz000/s3buXv//+mzfeeMOBUafOz8+PadOmceLECY4fP06jRo1o06YNZ8+eBbLf8SR37NgxvvvuO1555RWj5dn9uETOlla/prd06VJu3rxp+Gnbtq1h3dWrV2nVqhUNGzYkLCyM4cOH07dvX7Zt25bB0aefPfr17Hz85kyZMsXou3733XcN67LjuZulcsL5kDVefvllo+/5t99+M6zLaf2WPc4Tu3btytmzZwkNDWXz5s3s27eP/v37Z9YhZB4lcoQvvvhClSlTxvB63rx5Kl++fOrp06eGZWPHjlUVK1Z0RHhWWbp0qfL29jZZvnXrVuXk5KSioqIMy7799lvl5eVldJxZSe3atdXgwYMNrxMTE1WxYsXU1KlTHRiV7QC1fv16w2utVquKFCmipk+fblh2//595erqqlatWuWACG1z+/ZtBai9e/cqpXTHkDt3bvXTTz8Z2pw/f14B6tChQ44K02r58uVTixYtyvbH8+DBA1WhQgUVGhqqGjRooIYNG6aUyjnfk8j5UurXlDL9dzW5MWPGqJdfftloWefOnVVwcLAdI8xY6enXc8Lx65UqVUrNnj07xfXZ+dwtLTntfCg1kyZNUlWrVjW7Lqf3W7acJ547d04B6tixY4Y2v/zyi9JoNOrGjRuZFntmkDveOURMTAz58+c3vD506BCBgYG4uLgYlgUHB3Px4kXu3bvniBDT7dChQ1SpUoXChQsblgUHBxMbG2u4q5eVxMfHc+LECZo0aWJY5uTkRJMmTTh06JADI7Ofq1evEhUVZXSM3t7e+Pv7Z6tjjImJATD8P3TixAmePXtmdFwvvvgiJUuWzBbHlZiYyOrVq4mLiyMgICDbH8/gwYNp1aqVUfyQ/b8nIfQGDx5MwYIFqV27NkuWLEEpZVh36NAhk7/94ODgHPE3bkm/ntOOf9q0aRQoUIDq1aszffp0o2H1OfHcDZ6P86HkLl26RLFixShbtixdu3YlIiICeP76LUvOEw8dOoSPjw+vvvqqoU2TJk1wcnLiyJEjmR5zRsrl6ABE+l2+fJm5c+cyY8YMw7KoqCjKlClj1E7fsUVFRZEvX75MjdEeoqKijDpnMD6mrObOnTskJiaajfnChQsOisq+9J+7uWPMit+JOVqtluHDh1O3bl0qV64M6I7LxcXF5JnErH5cZ86cISAggCdPnuDh4cH69eupVKkSYWFh2fJ4AFavXs3Jkyc5duyYybrs+j0JkdSUKVNo1KgR7u7ubN++nXfeeYeHDx8ydOhQIOW+LzY2lsePH5MnTx5HhG0XlvTrOen4hw4dSo0aNcifPz8HDx5k/Pjx3Lx5k1mzZgE589wNno/zoaT8/f1ZtmwZFStW5ObNm0yePJn69evzxx9/PHf9liXniVFRURQqVMhofa5cucifP3+O+0zkjncWMm7cOLOTrCT9Sf4P1I0bN2jevDkdO3akX79+Doo8ZbYckxCZafDgwfzxxx8mkxllRxUrViQsLIwjR44waNAgevTowblz5xwdls2uX7/OsGHD+OGHH3Bzc3N0OEIA9u/XPvzwQ+rWrUv16tUZO3YsY8aMYfr06Rl4BOkj/boxaz6PkSNHEhQUxCuvvMLAgQOZOXMmc+fO5enTpw4+CmFPLVq0oGPHjrzyyisEBwezdetW7t+/z48//ujo0ISDyR3vLGTUqFH07Nkz1TZly5Y1/P7333/TsGFD6tSpYzLxRpEiRUxmSNS/LlKkiH0CtoC1x5SaIkWKmMyA6YhjslTBggVxdnY2+z1kxXhtoT+OW7duUbRoUcPyW7duUa1aNQdFZbkhQ4YYJvHw8/MzLC9SpAjx8fHcv3/f6Kp0Vv/uXFxcKF++PAA1a9bk2LFjzJkzh86dO2fL4zlx4gS3b9+mRo0ahmWJiYns27ePr7/+mm3btmXL4xLZmz37NXP8/f35+OOPefr0Ka6urin2515eXg6525vZ/XpWO/7k0vN5+Pv7k5CQQHh4OBUrVswy52729jycD6XGx8eHF154gcuXL9O0adPnqt+y5DyxSJEiJpPsJSQkEB0dneM+E0m8sxBfX198fX0tanvjxg0aNmxIzZo1Wbp0KU5OxoMXAgIC+OCDD3j27Bm5c+cGIDQ0lIoVK2bqUCVrjiktAQEBfPrpp9y+fdswJCU0NBQvLy8qVapkl/ewJxcXF2rWrMnOnTsNM9RqtVp27tzJkCFDHBucnZQpU4YiRYqwc+dOwz+gsbGxhjuuWZVSinfffZf169ezZ88ek6F9NWvWJHfu3OzcuZP27dsDcPHiRSIiIggICHBEyDbRarU8ffo02x5P48aNOXPmjNGyXr168eKLLzJ27FhKlCiRLY9LZG/27NfMCQsLI1++fLi6ugK6vm/r1q1GbUJDQx32N57Z/XpWO/7k0vN5hIWF4eTkZDj2rHLuZm/Pw/lQah4+fMiVK1fo1q1btu2PbWXJeWJAQAD379/nxIkT1KxZE4Bdu3ah1Wrx9/d3VOgZw9GzuwnrRUZGqvLly6vGjRuryMhIdfPmTcOP3v3791XhwoVVt27d1B9//KFWr16t3N3d1XfffefAyFN37do1derUKTV58mTl4eGhTp06pU6dOqUePHiglFIqISFBVa5cWTVr1kyFhYWpX3/9Vfn6+qrx48c7OPKUrV69Wrm6uqply5apc+fOqf79+ysfHx+jGVyzugcPHhi+C0DNmjVLnTp1Sl27dk0ppdS0adOUj4+P2rhxozp9+rRq06aNKlOmjHr8+LGDI0/ZoEGDlLe3t9qzZ4/R/z+PHj0ytBk4cKAqWbKk2rVrlzp+/LgKCAhQAQEBDow6dePGjVN79+5VV69eVadPn1bjxo1TGo1Gbd++XSmV/Y4nJUlnNVcq5xyXyJnS6td+/vlntXDhQnXmzBl16dIlNW/ePOXu7q4mTpxo2Mdff/2l3N3d1ejRo9X58+fVN998o5ydndWvv/7qqMOymD369ex8/EkdPHhQzZ49W4WFhakrV66olStXKl9fX9W9e3dDm+x47mapnHA+ZKlRo0apPXv2qKtXr6oDBw6oJk2aqIIFC6rbt28rpXJev2WP88TmzZur6tWrqyNHjqjffvtNVahQQXXp0sVRh5RhJPHOhpYuXaoAsz9J/f7776pevXrK1dVVFS9eXE2bNs1BEVumR48eZo9p9+7dhjbh4eGqRYsWKk+ePKpgwYJq1KhR6tmzZ44L2gJz585VJUuWVC4uLqp27drq8OHDjg7JKrt37zb7vfTo0UMppSsV8eGHH6rChQsrV1dX1bhxY3Xx4kXHBp2GlP7/Wbp0qaHN48eP1TvvvKPy5cun3N3dVbt27YwubmU1vXv3VqVKlVIuLi7K19dXNW7c2JB0K5X9jiclyRPvnHJcImdKq1/75ZdfVLVq1ZSHh4fKmzevqlq1qpo/f75KTEw02s/u3btVtWrVlIuLiypbtqzRv1VZmb369ex6/EmdOHFC+fv7K29vb+Xm5qZeeukl9dlnn6knT54Ytctu527WyO7nQ5bq3LmzKlq0qHJxcVHFixdXnTt3VpcvXzasz2n9lj3OE+/evau6dOmiPDw8lJeXl+rVq5fhAl1OolEqSc0KIYQQQgghhBBC2JXMai6EEEIIIYQQQmQgSbyFEEIIIYQQQogMJIm3EEIIIYQQQgiRgSTxFkIIIYQQQgghMpAk3kIIIYQQQgghRAaSxFsIIYQQQgghhMhAkngLIYQQQgghhBAZSBJvIYQQQgghhBAiA0niLbKkS5cu0a5dO4oWLYqTkxM+Pj6ODknkUEopatasSbNmzYyWBwUFodFoHBRV1ovDEuZi3bFjBxqNhq1btzooKiGEEEIIx5PEW1glPDwcjUZj9JM7d26KFy9Op06dOH78eLrfIzExkbZt27J161ZatWrFxIkTGTdunB2ifz589NFHJt9R8p+PPvrI0WFmGStWrODkyZNMmTLF0aHYZO3atWg0GjZv3uzoUMxq0qQJ9erVY8yYMSQmJjo6HCGEEEIIh8jl6ABE9lSuXDnefvttAOLi4jhx4gQ//fQTGzZsYMeOHQQGBtq876tXr3Lu3Dn69evHggUL7BXyc6d9+/ZUrlzZ7LqgoKDMDSaL0mq1fPTRR9SvX5/XXnvN0eHYZOPGjeTNm5cmTZo4OpQUjRkzhtdff53Vq1fTtWtXR4cjhBBCiFRotVr+7//+jxs3btC6dWvKlSvn6JByBEm8hU3Kly9vctd02rRpjB8/ng8//JC9e/favO+///4bgGLFiqUnxOdehw4dePPNNx0dRpb2yy+/EB4ezgcffODoUGySkJDAli1bCA4Oxs3NzdHhpKh58+YULFiQ+fPnS+IthBBCZHFvvPEGGzduBOCDDz5g9+7d1KpVy8FRZX8y1FzYTZ8+fQA4ceKEybr4+HhmzZpFjRo1yJs3L56entSvX5+ff/7ZqF3p0qVp0KABAJMnTzY7NNrSfQH07NkTjUbDX3/9xcyZM6lUqRKurq707NnT0Ob27duMGDGC8uXL4+rqSsGCBWnfvj1//PGHyf5Kly5N6dKlefjwIcOGDaNYsWK4urryyiuvsHbtWrOfS3x8PLNnz6ZWrVp4enri4eFBpUqVGDlyJPfu3TNqa00s9rJs2TI0Gg3Lli1j+/bt1KlTB3d3dwoUKECPHj24e/eu2e1Onz7Nm2++SdGiRXFxcaFUqVK8++67Ju31jyf07NmT8+fP065dOwoUKIBGoyE8PByAR48eMWbMGEqUKIGbmxuVK1dm4cKF7Nmzx+j7j4mJIW/evLz88stmY9JqtZQuXZp8+fLx+PHjNI996dKlaDQa2rdvb/HntWbNGlxdXalatSo3b940LFdKsXTpUurXr4+Pjw/u7u5UqFCBAQMGEBERYWh34sQJhgwZQuXKlfH29iZPnjxUqVKFadOm8ezZM4vjANi/fz/37t2jTZs2hmX656yfPn3K+++/T8mSJcmTJw81a9Zkx44dgO5zHDx4MMWKFcPNzY2AgACOHj1q9j3++OMPOnXqRKFChXB1daVMmTIMHz48xb8Lc3Lnzk3btm357bffuHz5slXHKIQQQojMc/ToUTZt2sSmTZuIjo6mQYMGTJw40dFh5Qhyx1vYXa5cxn9WT58+pXnz5uzZs4dq1arRp08fnj17xpYtW2jTpg1z585lyJAhAAwfPpywsDCWL19OgwYNDEOi9f+1Zl9Jvfvuuxw+fJhWrVoREhJCoUKFALhy5QpBQUFERkbSrFkz2rZty+3bt1m3bh3btm1j586d+Pv7G+3r2bNnNGvWjHv37tG+fXsePXrE6tWr6dSpE7/++qvRJF2PHz+madOmHDhwgAoVKtCrVy9cXV25dOkS3333Hd27dydfvnw2x2JPP//8M1u2bCEkJIQ6deqwb98+VqxYwZUrV/jtt99M2nbq1AknJyfatGlDiRIlOHfuHF9//TXbtm3jyJEjhuPSu3z5Mq+99hpVqlShZ8+e3L17FxcXFxITE2ndujW7d++mSpUqvPXWW0RHRzNq1CiTIfHe3t68+eabLFmyhIMHD1KnTh2j9aGhoVy7do3BgweTJ0+eVI9XKcXu3bupWLGiSawpmTt3LsOGDTNc6PH29gZ0CX/nzp1Zu3YtxYsXp0uXLnh5eREeHs6PP/5IixYtKFmyJAALFy5k06ZNBAYG0rJlSx49esSePXsYP348x44dY926dRbFArBhwwacnZ1p3bq1ybrOnTtz5swZXn/9dR4/fswPP/xA69atOXDgAP379yc+Pp6OHTvyzz//sGbNGpo3b87Vq1cNxwTw22+/ERwcTHx8PB06dKB06dIcOnSIOXPmsHnzZg4fPkzBggUtijUgIIBFixaxa9cuypcvb/ExCiGEECLz3Lp1i5IlSxrOLXr16sX777/v4KhyCCWEFa5evaoAFRwcbLLus88+U4Bq1aqV0fL3339fAerDDz9UWq3WsDw2Nla9+uqrysXFRd24ccOwfPfu3QpQkyZNMnkPa/fVo0cPBSg/Pz917do1k/3VqVNHOTs7q19//dVo+cWLF5Wnp6eqUqWK0fJSpUopQLVp00Y9ffrUsHzHjh1mP5dRo0YpQHXr1k0lJCQYrbt//7568OCBzbGkZNKkSQpQ7du3V5MmTTL7c/PmTUP7pUuXKkDlypVL/fbbb4blCQkJKigoSAHq0KFDhuV37txRXl5eqnjx4io8PNzovVetWqUANWTIEMMy/d8MoCZOnGgS76JFixSgWrRoYfQZnT17Vrm5uZn8LRw5ckQBqmfPnib76tChgwJUWFhYmp/T2bNnFaC6du1qdn2DBg1U0n8i9X977dq1U48fPzZqO3fuXAWoxo0bq0ePHhmte/Tokbp7967h9bVr10z+FrRarerdu7cCjL4Dc3EkVbp0aRUUFGS2fb169dTDhw8Ny9esWaMA5ePjozp27KiePXtmWPf5558rQM2cOdOwLDExUZUrV04BJn+To0ePVoDq3bu3xbH+/vvvClDdu3c3u14IkXPEx8erSZMmqfLlyysXFxcFqPXr1zs6LJGFabVaVaNGDdW0aVOj5amdE2Ym/blMjx49HBqHJdIb671791SpUqXUpk2bVHR0tGrZsqV68803jdpcuHBBOTs7q2+++cYOET8/JPEWVtH/z1yuXDlDEvfee++phg0bKkAVLlxYnTt3ztA+MTFR5cuXT5UrV84oUdb7+eefFaDmzp1rWJbSP7K27EufeM+ZM8ek/cmTJ80mD3ojR45UgDpz5oxhmT7x/uuvv0zalypVSuXPn9/w+tmzZ8rT01N5e3ur6Ohos++RnlhSok+8U/s5deqUob0+8TaXEOnXffXVV4Zls2bNUoBasWKF2fevUaOGKliwoOG1/m+mSJEiRhcr9PTJ/cmTJ03W9e/f3+zfQvXq1VXevHlVTEyMYdnt27eVi4uLqlWrVoqfTVLbtm1TgBo5cqTZ9fokMiEhQfXp00cBql+/fiZJs1JKvfTSS8rZ2Vn9+eefFr23OSdOnFCA+uijj8zGkVxYWJgC1OzZs82237t3r9HyxMRElTt3bgWYXISKiIgw+RvYt2+f4YJIcg8ePFD58+dXbm5uRt9paol3VFSUAlSjRo3MfwBCiAyX9EKo/idXrlyqWLFiqmPHjurYsWN2eZ+pU6cqQAUGBqr3339fTZo0SZ0/f94u+87pzH1HyX/u3bvn6DDtbtmyZSYX+pXKPon3sWPHTM5BHcUesX7xxReGv7eKFSuqyMhIkzZvv/22KlSokIqNjbVX6DmeDDUXNrly5QqTJ082WlakSBH2799vNIz04sWL3Lt3j2LFipm0B/jnn38AuHDhQprvmZ591a5d22TZ4cOHAd2QGnPltfT7uXDhgtHs4D4+PpQpU8akvZ+fH4cOHTLa/sGDBzRp0iTNocy2xpKaVatWWTW5Ws2aNU2W+fn5AXD//n2TWI8cOcKVK1dMtnny5Al37tzhzp07RsOQq1atiouLi0n733//nbx581K9enWTdXXr1jU7s/2AAQMYOHAg//vf/xg4cCCgKwsWHx9Pv3790jhSHf0zymnViG/fvj0bN27kgw8+4JNPPjFZ//DhQ86fP0/58uWpUKFCmu8bHx/P119/zerVq7lw4QIPHz5EKWVYr59cMC36SU+SPt+dVLVq1YxeOzk5UahQIR49emQY9q5XtGhRk/c+deoUYH4GfA8PD1599VW2b9/OxYsXqVKlSprx5s+fH4A7d+6k2VYIkbEysjIJwObNm/Hw8CA0NNTsv/sibUm/o+Sy8mSatsgpFUYg5T45K0kr1gcPHjBz5kw0Gg1KKapXr07x4sVN2o0ZM4aVK1fy1VdfZdtJajObJN7CJsHBwfz666+ALuFdvnw5Y8eO5fXXX+fo0aN4eHgAEB0dDcDZs2c5e/ZsivuLi4tL8z3Ts6/ChQunuL8tW7awZcsWi/eX9BnYpHLlyoVWqzW8jomJATD7j5W9YrEnLy8vk2X65/WT1l/Wx/rNN9+kur+4uDijxNvcdwAQGxtLiRIlzK5LaZu33nqL9957j0WLFhkS78WLF+Ph4UGXLl1SjUtP/wz4kydPUm23b98+3NzcaNmypdn11nzPoJttftOmTbzwwgt07tyZQoUKkTt3bu7fv8+cOXN4+vSpRfvZsGEDVapUMXsRCFL+PlP7npNO7hYbGwuk/B3ok3V9u7ToJ7tzd3e3qL0QIuNkZGUS0F3EK1CggCTd6WDuO8qpsnuFEdAlszVq1EjxfCYrSSvWzz77jFu3bjFixAi++uorwsLCzLarUqUKr7zyCgsXLmT8+PE4Ocmc3WmRT0ikm6+vL++99x7vv/8+58+fZ8KECYZ1+pP89u3bo3SPNpj9Wbp0aZrvk559aTSaFPc3d+7cVPfXo0cPmz4X/Z3UGzduWHxsGRWLPeljPXPmTKqxlipVymg7c9+Bfn/60QrJ3bp1y+xyT09PunbtyokTJwgLC+PAgQOcP3+eN99803DRJy2+vr7AfxcSUrJz507c3d1p3rw5Bw8eNFmvvxBjyfd87NgxNm3aRHBwMOfOnWPhwoV8+umnfPTRR1aNToiIiODUqVO0bdvW4m2spf+eU/oOoqKijNqlRf856z93IUTWklplEtBdhAwJCaFgwYK4urpSoUIFJkyYwKNHjwxtPvroIzQaDVevXuXatWuGyiSlS5e2el+AUWWLgwcP0qxZM3x8fEz6E1v2d/z4cZo2bYqnpyfe3t60a9fOUGnD3LG3bduWwoUL4+rqSokSJXjjjTdMJh61JhZ7Wrp0Kf7+/nh4eODh4YG/vz/Lli0zaWfN55mZx2tLhZGYmBgaNGiAk5MTc+fOtTr++Ph45s6dS3BwMCVKlMDV1ZVChQrxxhtvGEZ8Werq1aucOXPG6A5y8s+6YcOGeHp64uvryzvvvGO4GL1lyxYCAgLImzcvhQsXZsyYMSQkJJh9H0u/Z2tjTSo8PJzZs2dTqFAhJk+eTPny5bl06VKKlWI6derEtWvX2L17t1VxPK8k8RZ28/7771OsWDHmzZtn6LxeeuklvLy8OH78uNWlkpKz574AwwzhSYeH21PFihXx8vLi2LFjJmXDMjsWe7J3rFWrViUuLs7sFVVzia7egAEDAN0s4YsWLQKweJg5wMsvv4yTkxMXL15MtV316tXZtWsXLi4uNG/enAMHDhit15eHu3r1KpcuXUp1X/qh+a1atcLZ2dlo3f79+y2OXV86LyOHtOmH/u/Zs8dkXVxcHMePHydPnjxUrFjRov3pP2dLhqULIRwneWUSgG+//ZagoCAOHDhAq1atGDp0KH5+fnz66ac0bdqU+Ph4QPdoyqRJk/D29sbb25tJkyYxadIkhg8fbvW+kjp48KChVGL//v3p3LlzuvZ37NgxAgMDcXFxYcCAAbz66qts2LCBJk2amIyCmjNnDkFBQYSGhtK0aVNGjRpFo0aN+P33303KiNoSS3oNHTqU3r17c+PGDfr06UOfPn24ceMGvXr1YtiwYWa3Se3zzOzjVTZUGLl58yaBgYEcPnyYVatW8e6771odf3R0NMOHD+fp06e0bNmSESNGEBQUxNatW6lTpw7Hjh2zKBbQjUAD833ykSNHaNy4Md7e3gwYMICSJUvy7bff0q9fP9asWUOHDh0oVaoUAwYMwMfHh+nTp/PZZ5+Z7MeW79naWAHGjh3L06dPmTJlCp6enlSuXJnExEROnz5ttn1AQACgu0khLJCRD5CLnCe1Wc2VUmrOnDkmk4SNHTtWAWro0KEqPj7eZJszZ86oW7duGV6nNpGGtfvST6529epVs/H6+/srjUajVq9ebbIuMTFR7dmzx2hZqVKlVKlSpczuy9zEUvrZny2Z1dzaWFKin1xt1apVFrXXT6C2dOlSk3Xmvovbt28rT09P5evrq/744w+TbeLi4owmR0lrko+FCxcaZsNPTEw0LD9//rzZWc2TqlWrlvL29lZ58+ZVr7zyikXHm1S1atWUp6en0fvqJf8+f//9d1WwYEHl4eGh9u/fb9T2m2++UYBq0qSJyazmjx8/NsxqfvDgQQWoTp06GbX5448/VL58+cx+Tub+rpo0aaL8/PzMHlNqE5yl9vcLqAYNGhheJ53VPDQ01KjtuHHjrJ7VfPLkyQpQ27ZtM7teCJHxbKlMcvbsWZUrVy5VtWpVdefOHaN1+knUZsyYYbQ8pX9rrN2Xvg8C1JIlS+y6v+R9bbdu3Uz6zrCwMOXk5KSKFStmch6h1WqNqqjY8jmZY24S26Q/SfvXvXv3KkC99NJL6v79+4bl0dHR6oUXXlCA2rdvn9njN/d5OuJ406owkvw85OLFi6p06dLK09PTpG+yJv4nT56YnTDsjz/+UB4eHqpJkyZGy1M7l2nQoIEqXbq02bgBtWHDBsPy+Ph49corryiNRqMKFiyojh49algXGxurChUqpPLnz290jmvt92xtrHoHDhxQgKpUqZLhnFV/Tjl//nyz28TExBgmUhRpk8RbWCWtxPvx48eqWLFiKleuXOry5ctKKd0/bk2bNjV0JL169VJjx45Vb7/9tqpatarJLJapJd7W7iutxPuvv/4yzFT+2muvqXfeeUeNGjVKdezYUfn5+SlXV1ej9tYm3o8fP1b169dXgKpQoYIaOnSoGj16tGrfvr3Kmzev0ezi1saSEkvKiSU9sbA28VZKqc2bN6s8efIoZ2dn1apVKzVq1Cg1ZMgQ1bp1a+Xp6Wn095FW4p2QkKACAwMVoF555RU1duxY1a9fP+Xp6alCQkIUoCZPnmx228WLFxs6NltmEtUngwcOHDBZZ+77PH36tPL19VUeHh5GnZxWq1WdOnVSgCpevLgaNGiQGjt2rOrSpYvKnz+/oYxOQkKCql27tgJU/fr11ejRo1Xnzp1Vnjx5DKXQ0kq87927p3Lnzq3eeecds8dkr8RbKaX279+v3N3dVe7cudVbb72lxo8fb5iFvly5cur27dsWv3e9evVUvnz5TEqxCSEyj7WVSZRSaujQoSYn9nqJiYnK19dX1axZ02h5Sv/WWLsvfR9Uo0YNs8dj6/7MJQn6dUkrXQwaNCjFJDW9saQkrVnNk1ay0JehXLNmjcl+fvjhB5MLpGl9no443rQqjCQ9Dzl69Kjy9fVVvr6+6vjx4+mKPzUhISHKxcXFKPlN6Vzmzp07ytnZWQ0bNsxs3A0bNjTZ/5QpUxSgevXqZbJO/50mrZ5j7fdsbaxK6c5j9OcnW7duNSxfu3atAtTAgQNNttFzc3NTZcuWTXG9+I9Mribsys3NjfHjx/Puu+8yefJkVqxYgaurK7/88guLFy9mxYoVrFu3jqdPn1K4cGEqVarEwIEDLR5+as99AZQpU4ZTp04xa9YsNmzYwNKlS3F2dqZo0aIEBgbSoUMHWz8KQPd5hIaG8vXXX7Ny5UoWLlyIs7MzJUuWZODAgUbPvdk7lnXr1rFu3Tqz69q0aWPVM8XJtWrVilOnTjF9+nR27NhBaGgoefPmxc/Pj169eqU4E6s5zs7ObN26lUmTJrFq1Sq+/PJLypUrx8yZM8mfPz+bNm1K8TniN998k3feeQcnJyer3lOvb9++fPzxx6xcuZI6deqk2b5KlSrs2rWLxo0b06JFC7Zu3UpgYCAajYbVq1fTrFkzFi1axIoVK1BKUbx4cTp16mSYMd7Z2ZnNmzczbtw4fv31V44dO0aFChWYMWMGLVq0MBnGZ87WrVt59uxZhj7frVevXj0OHz7MlClT2L59OzExMRQrVoxhw4YxYcIEo8nzUhMeHs6BAwcYNmxYjpuNV4jsyNLKJPBfJYtt27aZHU6aO3duiyqTpGdftWrVsuv+LK3icfToUQCaNWtm9v3tEUtKkk5im5LUqk80bNgQwOxjXCl9no44XksrjOzfv5+ZM2fi6+vLtm3bzFYRsSZ+0H02X3zxBb/99htRUVEmjzHeuXPHMJFoSrZs2UJiYqLFFUbgv8lJU1v3999/GyZPtfV7tibW//3vfxw9epSmTZvSokULw3J9JZ3U9p8/f36pWGIpR2f+QgiRkg8++MDk6mtS+lqU3bp1s/k93n77bZUvX75sU4eyU6dOytvb2+yjFlnVBx98oHLnzm0YBSOEcAxzo9Zu376tpk+frpycnNRLL71k9AiUUkqVL18+1Tuw+p+kUrrjbe2+9HcNJ06caPZ4bN2fuRF15u4Sli9fXmk0GrOPI6U3lpSkNbIwqXLlyiknJyel1WpN1iUmJiqNRqPKly9vWGbJ55nZx7t+/XoFqPfff9/sen3M+sex3njjDZNH92yJ/8CBA8rV1VW5urqqkJAQNXLkSDVx4kQ1adIkwwjKpKMlU7qL3K5dO5U/f3717Nkzs3Gb+1tLbaShftTi7t27Dcus/Z6tjfXRo0eqRIkSysnJSf3+++9G6xISEpSbm5vKmzdvip9rvnz5VJEiRcyuE8ZkcjUhhMPdvHnTZNm5c+f46quv8PHxMXuVF2D69OkADBo0yOb3/uSTT3j8+LHJrKhZUXx8PL/++istWrQgd+7cjg7HIvfu3WPu3LkMGjSIcuXKOTocIUQyqVUmgf8qF8TGxqZaycIStu4rtaoY9orNHB8fH5RSZvuozI4lpffUarVmK4Pcvn0bpZTZEWMpfZ6OOF5LK4wMGTKEPn368H//93+89dZbZmf+tib+Tz/9lKdPn7Jjxw5+/vlnZs6cyeTJk/noo48oUqRImtuDrhzp9u3badWqldlJCe3F1u85qdRinTFjBtevX0er1VK1alVDNQKNRkOuXLl48uQJcXFxZieQ1Wq1xMTESMUSC0niLYRwuEGDBlGtWjX69+/P2LFj6dChA9WrV+fhw4fMmjXLUHMbdKW0pk2bRrdu3fjxxx8JDg42zKppi1KlSrF8+XI8PT3tcSgZysXFhZiYGFatWuXoUCx29epVRowYwcSJEx0dihAiFeYqk8B/lSz0Q4vTw577yoj9JVe7dm0Atm/f7vBYzEmt+oR+mbnhzClxxPFaWmHEycmJhQsX0q9fP3788Ue6du1qknxbE/+VK1fInz8/9erVM1r+6NEjTp48aVHsO3bsIC4uLkMrjIB9vueUYr158yZffPEFefPmNcyWnvzn5ZdfBswPN7906RJarVYqllgq426mCyGEZVauXKnq1aunChQooHLlyqV8fHxU06ZN1a+//mrSVj98y8PDQ4WEhKibN286IGIhhMh+bKlMcubMGZUrVy5VsWJFde3aNZNt7t27p06ePGm0LKWh5tbuK7Xhuvben7nhuadPn1bOzs6qWLFiKjw83Kh98lmybfmczLFmqLl+tutKlSqpmJgYw/L79++rF198UQFq7969huVpfZ6OOF6lUq8wkjxmrVarBgwYoADVoUMHo2HT1sTfrFkzpdFojKqzJCQkGCZow4Kh5n379lWurq4mj2eYizspa4eaW/s9WxNrr169FKCmTp1qEoverFmzFKDGjRtnsm758uUKUN99912K24v/yORqQgiH69q1K127drWobVBQkN2H6wkhhID+/fvz+eefs2LFCt5//33KlStH5cqVmTdvHoMGDaJixYq0bNmScuXK8eDBA/766y/27t1Lz549mT9/fpr7t+e+MmJ/yVWpUoUvv/ySoUOH8vLLL9O2bVtKlSpFVFQU+/bto1WrVnz55ZeZEos5gYGBvPvuu8ydO5fKlSvTvn17lFKsW7eOyMhIhg4dSmBgYJY/3nbt2jFp0iQOHz6c5kSnGo2Gb7/9FicnJ7799luUUqxevZpcuXJZFf+7777L9u3bqVevHp06dcLNzY09e/Zw48YNgoKCzN5dTkqr1bJp0yYaN26Mh4eHJR+vzdL7PacU66lTp1i+fDkvvPACI0eOTHH71O54h4aGkitXLlq3bm37AT5PHJv3CyGEEEKIzGDJ3dS5c+eanbTy6NGj6s0331TFihVTuXPnVgULFlQ1atRQ48aNU+fPnzdqm1rpQmv2ldYdWnvuL7XSl7t371atW7dW+fPnVy4uLsrPz0+1b9/ebClKaz4nc6y54623ZMkSVatWLeXu7q7c3d1VrVq1zJbUsvTzzMzjVUqpGzduqFy5cqlBgwZZHLNWq1WDBw82TLiWdMJRS+Nfu3atqlGjhnJ3d1cFCxZUnTp1UleuXDFbijb534e+5vWCBQtS/AxT+qytveOtZ+n3bGms+vKgv/zyi9lj0Ltx44YCTCZQi4uLUx4eHqpt27apbi/+o1FKbh0JIYQQQgghHKNbt25s2bKFa9euZYs5V8aOHcv06dP5+++/LZ6MzVEyKtZFixbRr18/9u7da9XIiueZJN5CCCGEEEIIh7l27RovvvgiH374Ie+//76jw0nTiy++SL58+Th06JCjQ0lTRsSakJDACy+8QJUqVdi4caPd9pvTyTPeQgghhBBCCIfRVxi5deuWo0OxyIULFxwdgsUyItaIiAi6d+9Ot27d7L7vnEzueAshhBBCCCGEEBlI6ngLIYQQQgghhBAZSBJvIYQQQgghhBAiA0niLYQQQgghhBBCZCBJvIUQQgghhBBCiAwkibcQQgghhBBCCJGBJPEWQgghhBBCCCEykCTeQgghhBBCCCFEBpLEWwghhBBCCCGEyECSeAshhBBCCCGEEBno/wGa4z7joh3aWgAAAABJRU5ErkJggg==\n"
},
"metadata": {}
}
],
"source": [
"import matplotlib.pyplot as plt\n",
"\n",
"fig, ax = plt.subplots(1,2,figsize=(10,5))\n",
"\n",
"e1 = energy.cpu().detach().numpy() + np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy_sqm.npy\",\"rb\")) * 27.2114 * 23.061\n",
"e2 = ene_pred.cpu().detach().numpy() + np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy_sqm.npy\",\"rb\")) * 27.2114 * 23.061\n",
"\n",
"ax[0].plot(e1, e2, linestyle='none', marker='.', color='springgreen')\n",
"ax[0].plot([np.max(e1), np.min(e1)], [np.max(e2), np.min(e2)] , color=\"k\", linewidth=1.5)\n",
"ax[0].set_xlabel(\"Reference Energy (kcal/mol)\", size=14)\n",
"ax[0].set_ylabel(\"Predicted Energy (kcal/mol)\", size=14)\n",
"ax[0].annotate('RMSD: %.3f' % np.sqrt(np.mean((e1 - e2)**2)), xy=(0.05, 0.95), xycoords='axes fraction', size=14)\n",
"\n",
"f1 = -qm_gradient.cpu().detach().numpy().reshape(-1) - np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad_sqm.npy\",\"rb\")).reshape(-1) * 27.2114 * 23.061 / 0.529177249\n",
"f2 = -grad_pred.cpu().detach().numpy().reshape(-1) - np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad_sqm.npy\",\"rb\")).reshape(-1) * 27.2114 * 23.061 / 0.529177249\n",
"\n",
"ax[1].plot(f1, f2, linestyle='none', marker='.', color='springgreen')\n",
"ax[1].plot([np.max(f1), np.min(f1)], [np.max(f2), np.min(f2)] , color=\"k\", linewidth=1.5)\n",
"ax[1].set_xlabel(r'Reference Force (kcal/mol/$\\AA$)', size=14)\n",
"ax[1].set_ylabel(r'Predicted Force (kcal/mol/$\\AA$)', size=14)\n",
"ax[1].annotate('RMSD: %.3f' % np.sqrt(np.mean((f1 - f2)**2)), xy=(0.05, 0.95), xycoords='axes fraction', size=14)\n",
"\n",
"plt.tight_layout()\n",
"plt.savefig('rmsd.png', dpi=300)"
]
},
{
"cell_type": "markdown",
"source": [
"### The Model Weights and Biases Dictionary\n",
"\n",
"This cell prints the size of the weights and biases used in the trained model for reference."
],
"metadata": {
"id": "Ifal2I5wMDU8"
}
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {
"id": "RLr5VkQCPoBO",
"colab": {
"base_uri": "https://localhost:8080/"
},
"outputId": "8d6124b9-4c62-4bb9-b340-68777627976e"
},
"outputs": [
{
"output_type": "stream",
"name": "stdout",
"text": [
"Model's state_dict:\n",
"fitting_net.fitting_net.0.weight \t torch.Size([3, 240, 48])\n",
"fitting_net.fitting_net.0.bias \t torch.Size([3, 240])\n",
"fitting_net.fitting_net.1.weight \t torch.Size([3, 240, 240])\n",
"fitting_net.fitting_net.1.bias \t torch.Size([3, 240])\n",
"fitting_net.fitting_net.2.weight \t torch.Size([3, 240, 240])\n",
"fitting_net.fitting_net.2.bias \t torch.Size([3, 240])\n",
"fitting_net.fitting_net.3.weight \t torch.Size([3, 1, 240])\n",
"fitting_net.fitting_net.3.bias \t torch.Size([3, 1])\n"
]
}
],
"source": [
"print(\"Model's state_dict:\")\n",
"for param_tensor in model.state_dict():\n",
" print(param_tensor, \"\\t\", model.state_dict()[param_tensor].size())"
]
},
{
"cell_type": "markdown",
"source": [
"## Plotting the Minimization of the Loss Function"
],
"metadata": {
"id": "kM7z96Vswymb"
}
},
{
"cell_type": "markdown",
"source": [
"### Plotting Validation Error for $\\Delta$MLP\n",
"\n",
"Validation error for the $\\Delta$MLP is shown below."
],
"metadata": {
"id": "fnqPBH5iMI3p"
}
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {
"id": "xzYcSyS4PrE2",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 855
},
"outputId": "e6411291-147d-466c-c680-858cf25c05c0"
},
"outputs": [
{
"output_type": "display_data",
"data": {
"text/plain": [
""
],
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAj4AAANGCAYAAAD9NIS0AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAC29ElEQVR4nOzdd1yW9eL/8dcNiLjAjYKCeyuaipoTtIxS02xq6dHK6qedks5pnWN7nsZJy8a3HA07WuYoy9Rw5Z6Ue5sKCuIAAQXhvn5/XIIioIwL7sH7+Xjcj3tc1319PtwW95vPtBmGYSAiIiJSBng4ugIiIiIipUXBR0RERMoMBR8REREpMxR8REREpMxQ8BEREZEyQ8FHREREygwFHxERESkzFHxERESkzPBydAXEZLfbiY2NpUqVKthsNkdXR0RExGUYhsG5c+cICAjAw+PabToKPk4iNjaW+vXrO7oaIiIiLuvo0aPUq1fvmuco+DiJKlWqAOY/mq+vr4NrIyIi4jqSkpKoX79+9nfptSj4OIms7i1fX18FHxERkSIoyFARDW4WERGRMkPBR0RERMoMBR8REREpMxR8REREpMxQ8BEREZEyQ8FHREREygwFHxERESkzFHxERESkzFDwERERkTJDwUdERETKDEu3rFi2bBlRUVGsXr2aY8eOkZCQQMWKFalVqxZt27ald+/eDBgwgDp16lhZrIiIiEiB2AzDMIpzgZSUFCZNmsTnn3/OX3/9RdblfHx8qF69OufPnycxMRG73Q5AuXLlGDhwIOPHj6d79+7F/wncRFJSEn5+fiQmJjrVXl1JabDuGPQOhvLa2U1ERJxQYb5Di9XV9emnn9KkSRP+9a9/4evry6uvvkpUVBSJiYmkpqZy7NgxTp06xcWLF9m9ezdffvkld999N4sXL6ZXr17ccccdHDp0qDhVkBL24QZ4eAHM2e3omoiIiBRfsYLP448/zk033cSff/5JdHQ0zz//PGFhYbm2hbfZbDRr1owHHniAr7/+mri4OD777DP++OMPvv7662L9AFKyjidfuj/n2HqIiIhYoVidFzt27KBZs2aFfl+FChV46KGHGDVqFEeOHClOFaSEpaSb9+czHFsPERERKxSrxacooedKnp6eNGzYsFjXkJKVetG8v6DgIyIibkDT2eWaUi4FH7X4iIiIOyhWV1dxuqmCgoKKU7SUErX4iIiIOylW8GnQoAE2m63Q77PZbGRk6JvUFWS3+Fx0bD1ERESsUKzgM2LEiCIFH3EdqRrcLCIibqRYwWf69OkWVUOckWFojI+IiLgXDW6WfKVlQualdb0vqKtLRETcQIltQhATE0N0dDRJSUn4+vrSvn17AgMDS6o4KQGpV4QdtfiIiIg7sDz47N+/n8cee4ylS5fmOta3b18+/vhjmjRpYnWxUgJSFHxERMTNWBp8jh49So8ePYiPj6dFixb06tWLunXrcuLECVauXMlvv/1Gz5492bBhA/Xr17eyaCkBV87k0qwuERFxB5YGn5dffpn4+Hg+/vhjHnnkkVwzvj777DMee+wxXnnlFT7//HMri5YScGWLj9bxERERd2Bp8Fm0aBEDBw7k0UcfzfP4I488wi+//MLChQutLFZKSNY+XXBpoLMdPDUcXkREXJilX2Px8fG0adPmmue0adOGkydPWlmslJDUq7q31OojIiKuztLgU6tWLXbu3HnNc3bu3EmtWrWsLFZKSMpVwUcDnEVExNVZGnz69+/Pjz/+yJQpU/I8PnXqVH766SduueUWK4uVEnJ1i4+Cj4iIuDqbYRiGVRc7cuQInTp14tSpU7Rq1YrevXvj7+9PXFwcK1euZMeOHdSsWZNNmzZpVtdVkpKS8PPzIzExEV9fX0dXB4D/2wKv/375+ZL7oVkNx9VHREQkL4X5DrV0cHNQUBCrV6/mkUceYfny5ezYsSPH8bCwMD755BOFHheRmp7zucb4iIiIq7N8AcOmTZuydOlSjh49mmvlZgUe16IxPiIi4m5KbMuK+vXrK+i4uFxjfLSIoYiIuLgSCz7ivAwDouNg9k5YdAD6BMO7N+c+T4ObRUTE3VgefA4dOsTEiRP5448/iI2N5eLF3M0ENpuNAwcOWF20XEdaBkyLhu92woEzl19fsC/v4KOuLhERcTeWBp9ff/2VwYMHk56eTrly5ahduzZeXrmLsHAimRTC3N3w5mrzsY8XhDeAX/abgSY9E7w9c55/dYtPmoKPiIi4OEuDzzPPPIOnpyezZs1i6NCheHhofwNn8leied+/Mbx3E1QsB40+NF87lwY1KuY8P6vFp7ynuWWFxviIiIirszSZ7N27l2HDhnHXXXeV+dCzYMECmjdvTtOmTfniiy8cXR0Ajieb9x3qQJXy5r5blb3N15LScp+fNZ291qVApK4uERFxdZa2+NSpUwcfHx8rL+mSMjIyiIyMZNmyZfj5+dGxY0eGDBlCjRqOXf3vxKXgU6fy5dd8vSE5Hc6l5z4/q8WnRkU4dk7BR0REXJ+lzTLDhg1j4cKFXLhwwcrLupwNGzbQunVrAgMDqVy5MhERESxevNjR1SIur+BT3rzPs8XnUvCpXsG8V1eXiIi4OkuDz0svvUSLFi3o378/q1evJjk52crL5/DWW29hs9l48sknLb3uypUrGThwIAEBAdhsNubNm5fneZMnT6ZBgwb4+PjQpUsXNmzYkH0sNjaWwMDA7OeBgYHExMRYWs/CMgw4kWI+rlPp8utVLgWfxDyCT1aLT81LwUcrN4uIiKuzNPiUK1eOv//972zbto1evXrh5+eHp6dnrlteM70KY+PGjXz22We0a9fumuetXr06z+n0O3fuJC4uLs/3pKSkEBISwuTJk/O97qxZs4iMjOTFF19ky5YthISE0L9/f+Lj4wv3g5Sic+mXW3DyavE5d1XwybRfDjo1NMZHRETchKVjfGbNmsXw4cOx2+00atSIunXrFjvkXC05OZnhw4fz+eef89prr+V7nt1uZ+zYsTRt2pSZM2fi6WnO1d6zZw/h4eFERkby9NNP53pfREQEERER16zD+++/z8MPP8yoUaMA+PTTT/n555+ZOnUqzz77LAEBATlaeGJiYggNDS3Kj2uZrPE9vuWhQrnLr2d3dV01xufKqezZwUddXSIi4uIsTSWvvPIKfn5+/Prrr3Tu3NnKS2cbO3Yst912G/369btm8PHw8OCXX36hV69ejBgxgq+//ppDhw4RHh7O4MGD8ww9BZGens7mzZt57rnncpTVr18/1q5dC0BoaCjbt28nJiYGPz8/Fi5cyIQJE/K83uTJk5k8eTKZmZlFqk9BZQWfupVzvp7fGJ+s4ONhg6qXzlGLj4iIuDpLg8+hQ4cYNWpUiYWemTNnsmXLFjZu3Fig8wMCAli6dCk9e/Zk2LBhrF27ln79+vHJJ58UuQ4JCQlkZmbi7++f43V/f392794NgJeXF++99x5hYWHY7XaefvrpfGd0jR07lrFjx5KUlISfn1+R63U9ec3oAqiSz3T2rOBTqZy53g8o+IiIiOuzNPjUr1+/xFoujh49yhNPPMGSJUsKNWU+KCiIr7/+mt69e9OoUSOmTJmCzWYrkTpeadCgQQwaNKjEyymorIHN/pVyvp7fGJ+sgc0Vy5mrPANcUFeXiIi4OEsHNz/88MP89NNPnD592srLArB582bi4+O54YYb8PLywsvLixUrVjBp0iS8vLzyDVxxcXGMGTOGgQMHkpqayvjx44tVj5o1a+Lp6ZlrcHRcXBx16tQp1rVLUl5T2eH6XV2Vrgg+avERERFXZ2mLz5133snq1avp3r07//73vwkJCcHX1zfPc4OCggp17b59+7Jt27Ycr40aNYoWLVpkb5VxtYSEBPr27UvLli35/vvv2bt3L3369KF8+fK8++67hSo/i7e3Nx07diQqKorBgwcD5kDqqKgoxo0bV6Rrlob8urryCz7ZLT7elwdDK/iIiIirszT4NGrUCJvNhmEYjBgxIt/zbDYbGRmF+xatUqUKbdq0yfFapUqVqFGjRq7XwQwjERERBAcHM2vWLLy8vGjVqhVLliwhPDycwMDAPFt/kpOT2b9/f/bzQ4cOER0dTfXq1bPDWmRkJCNHjqRTp06EhobywQcfkJKSkj3Lyxkdzy/4FGCMT4WsFh91dYmIiIuzNPiMGDGiVMbPFISHhwdvvPEGPXv2xNvbO/v1kJAQfvvtN2rVqpXn+zZt2kRYWFj288jISABGjhzJ9OnTAbjnnns4efIkL7zwAidOnKB9+/b8+uuvuQY8O5PrdXVdvWVFyqXnFbwuBx8tYCgiIq7O0uCTFQxKy/Lly695/Kabbsrz9Q4dOuT7nj59+mAYxnXLHjdunFN3bV0pPRMSzpuP6+QzuDm/rq5K6uoSERE3UuzBzR9//LHDt2OQa4u/NKPL2/PyvltZqlzR4pNpv/x66hWzurJafDLscLFklxsSEREpUcUOPuPGjSMoKIjOnTvz+uuv5xqALI6XNbC5diW4uieyyuVeQJKv6O5KyWNWF6jVR0REXFuxg8/GjRt5/vnnSU9PZ8KECbRv357GjRvz1FNPsWLFCux2+/UvIiUqv1WbAcp7XQ42V25bceXgZm9PcwVnUPARERHXVuzg07FjR1599VX++OMPDh48yLvvvktQUBCTJk0iPDwcf39/Ro0axbx580hNTbWizlJI+U1lz5LXOJ+swc0Vy5mtRBW0iKGIiLgBSxcwbNCgAePHj2fZsmXExcUxbdo0evbsyezZs7njjjuoWbMmAwcOZOrUqU69k7m7yW/V5ix5bVuR1bJT6dKxClrEUERE3IClwedK1atXZ8SIEcyZM4eEhAR+/PFHhg8fzqZNm3jooYcICAigR48eJVW8XCG/qexZ8tq24soWHwCfS/ea0i4iIq7M0uns+SlfvjwDBgxgwIABGIbBunXrmDdvHj/++GNpFF/mFaWr68oxPqAWHxERcQ8l1uKTH5vNRrdu3Xj77bfZtWtXaRdfJuW3anMWv7zG+FwxnR20erOIiLiHYrX4HDlypMjvLexeXVI0hnF5HZ/8gk9eY3xSrw4+WsRQRETcQLGCT4MGDYq0RUVR9uqSojlzAdIuLTqY3+Dm7K6ufNbxgctT3jXGR0REXFmxgo8z7c0lecsa31OjgrkeT17yHOOTNbj56lld6uoSEREXVqzgU9p7c0nhZQUf/3y6uSB38DGM3C0+6uoSERF3UOqDm6V0XWvV5ixVrgo+aZmQeWmf1lyDmxV8RETEhSn4uLnsqez5jO+BK9bxudS9lXpFd9bVwUcrN4uIiCuzfB2fzMxMvvvuO3777TdiY2NJS0vLdY7NZiMqKsrqoiUP2as2F6KrKyv4lPcEr0vR2EddXSIi4gYsDT4pKSncfPPNrFu3DsMwsNlsGIaRfTzruQZEl57rLV4IuaezZy9eeMXO7erqEhERd2BpV9drr73G2rVrefnll0lISMAwDF566SWOHz/OrFmzaNSoEXfddVeerUBSMq63XQVcXsDwXFrOgc1Z3VxweTq7ZnWJiIgrszT4zJkzh65du/Lvf/+b6tWrZ7/u7+/PXXfdxbJly/jtt9945513rCxWriGrq+tag5uzuroyDbO1J2ufrkpXBB+1+IiIiDuwNPgcOXKErl27Xr64h0eO1p169epx22238eWXX1pZrOTjQgacvWA+vtYYHx8vKHfpv4SktNyrNsPl6exawFBERFyZpcGnUqVKeHhcvqSfnx/Hjx/PcU6dOnWKtdWFFFzW+J4KXuDrnf95NlvOKe3q6hIREXdlafAJDg7OEWratGnD0qVLs1t9DMMgKiqKunXrWlms5OPKgc3XG0/ue8UA56t3Zgd1dYmIiHuwNPj07duXZcuWZe/DNXLkSI4cOUK3bt345z//SY8ePYiOjmbo0KFWFiv5KMiqzVmu3K8rrxYfrdwsIiLuwNLp7A8//DA1atTg5MmT1K1bl9GjR7N161Y+/vhjoqOjARg6dCgvvfSSlcVKPgoysDnLlWv5pF5jcLMWMBQREVdmafBp2rQpzzzzTI7XPvzwQ1544QUOHjxIcHAwderUsbJIuYaCrNqcJc8xPlrHR0RE3IzlKzfnpVatWtSqVas0ipIrFKWr61x+Y3zU1SUiIm7A0jE+O3fuZNKkSZw8eTLP4/Hx8UyaNIldu3ZZWazko2ZFaOAH9X2vf+6VY3zyms5+5ayuKxbjFhERcSmWtvi89dZbREVFMW7cuDyP16hRg3feeYetW7cybdo0K4uWPLwWVvBzffPo6sprjI8BpGdC+VJpKxQREbGWpS0+v//+O3379s2xls+VPD096du3LytXrrSyWLFAlTyms185xsfniqCjRQxFRMRVWRp8Tpw4Qf369a95TmBgYK5FDcXxrtyvK3tw8xVhp5zn5dWdNc5HRERcleUrN8fHx1/znPj4eHx8fKwsVixwvenscMXMLk1pFxERF2Vp8LnhhhuYN28eZ8+ezfP4mTNnmDt3LjfccIOVxYoF8hrjU/GqbS58NLNLRERcnKXBZ+zYsZw6dYqwsLBc43hWrFhBWFgYZ86cyXfwszhOXmN88m3xUfAREREXZencnNtvv53x48fz3//+l7CwMMqXL0+dOnU4ceIEaWlpGIbBP//5TwYPHmxlsWKB7HV80i/v61VRXV0iIuJmLG3xAXjvvff48ccf6d+/P5UqVeLYsWNUrlyZiIgIfv75Z95++22rixQLZAWftMzLs7Zytfhceq5ZXSIi4qpKZDWWAQMGMGDAgJK4tJSQSt5gw1yn58rXruSjri4REXFxlrb47N27t0DnzZ4928pixQIetsv7dWU9L++Z8xx1dYmIiKuzNPjcfPPN112jZ/bs2QwfPtzKYsUivlcEn0rlLo/1yaL9ukRExNVZGnzOnj1L//79SUxMzPP4nDlzGDZsGA0bNrSyWLHIlcHn6oHNoK4uERFxfZYGn3nz5rFv3z4GDhxIWlpajmNz587l3nvvpUGDBixbtszKYsUivleM6bl6YDNc7uq6oK4uERFxUZYGnz59+vDNN9+wZs0a7rnnHux2O2AGonvuuYfg4GCWL19O3bp1rSxWLHJli08FtfiIiIgbsnw6+9ChQ/noo4/48ccfGTNmTHboCQoKYtmyZQQEBFhdpFjk6jE+V9MYHxERcXUlMp390UcfJS4ujpdffplp06Zld2/Vq1evJIoTi1xvjI9mdYmIiKsrVvA5cuRIvsdGjRpFdHQ0v//+O9OnT8cwjBznBwUFFadoKQFVrhzj4537ePYYH7X4iIiIiypW8GnQoAG2q+c8X8UwDPr06ZPjNZvNRkaGvj2dzXVbfNTVJSIiLq5YwWfEiBHXDT7iOq43xsdHXV0iIuLiihV8pk+fblE1xBlcd3CzZnWJiIiLs3xWl7iuKurqEhERN1es4GMYxvVPKoVriDVytPhcY3BzmoKPiIi4qGIFnzZt2vD9998X6b1Hjx7l0Ucf5e233y5OFcRCfprOLiIibq5Ywadp06bcc889NGrUiBdffJFt27ZdswXn1KlTzJw5kwEDBtCkSRPmz59Pp06dilMFp7VgwQKaN29O06ZN+eKLLxxdnQK5cjp7nnt1qatLRERcnM0oZl/TihUrmDBhAqtWrcJms1GpUiXat2+Pv78/VatW5cKFC5w+fZo9e/Zw6NAhAKpVq8b/+3//j6effprKlStb8oM4k4yMDFq1asWyZcvw8/OjY8eOrFmzhho1auT7nqSkJPz8/EhMTMTX17cUa3tZhh0af2g+njoI+l61l+yxJOg+zZzdtWds6ddPREQkL4X5Di32ys29e/dm5cqV7Nixg2nTprF06VLWrFmTvU9Xlho1anD77bczZMgQ7r77bsqXL5/PFV3fhg0baN26NYGBgQBERESwePFi7rvvPgfX7Nq8PMzZXCkXr7NJaQbYDfDQSgYiIuJiLJvV1bp1a9599122bNlCYmIie/bsYc2aNWzdupVjx45x8uRJ5syZwwMPPFDk0PPJJ5/Qrl07fH198fX1pVu3bixcuNCqHwGAlStXMnDgQAICArDZbMybNy/P8yZPnkyDBg3w8fGhS5cubNiwIftYbGxsdugBCAwMJCYmxtJ6lhT/SuZ9zYq5j125cakGOIuIiCsqkenslSpVomnTpnTt2pWQkBDLNiatV68eb731Fps3b2bTpk2Eh4dz++23s2PHjjzPX716NRcv5h6Ju3PnTuLi4vJ8T0pKCiEhIUyePDnfesyaNYvIyEhefPFFtmzZQkhICP379yc+Pr5oP5gT+W9/+O/N0KR67mM+V7QPapyPiIi4Ipdax2fgwIHceuutNG3alGbNmvH6669TuXJl1q1bl+tcu93O2LFjGTZsGJmZmdmv79mzh/DwcL788ss8y4iIiOC1115jyJAh+dbj/fff5+GHH2bUqFG0atWKTz/9lIoVKzJ16lQAAgICcrTwxMTEuMyu9O3rwB0t8z7mYYPynuZjzewSERFX5FLB50qZmZnMnDmTlJQUunXrluu4h4cHv/zyC1u3bmXEiBHY7XYOHDhAeHg4gwcP5umnny5Suenp6WzevJl+/frlKKtfv36sXbsWgNDQULZv305MTAzJycksXLiQ/v3753m9yZMn06pVKzp37lyk+pQ2LWIoIiKurNiDm0vbtm3b6NatGxcuXKBy5crMnTuXVq1a5XluQEAAS5cupWfPngwbNoy1a9fSr18/PvnkkyKXn5CQQGZmJv7+/jle9/f3Z/fu3QB4eXnx3nvvERYWht1u5+mnn853RtfYsWMZO3Zs9oh0Z1fBC86i4CMiIq7J5YJP8+bNiY6OJjExkdmzZzNy5EhWrFiRb/gJCgri66+/pnfv3jRq1IgpU6aUysaqgwYNYtCgQSVeTmnLntmlri4REXFBLtfV5e3tTZMmTejYsSNvvvkmISEhTJw4Md/z4+LiGDNmDAMHDiQ1NZXx48cXq/yaNWvi6emZa3B0XFwcderUKda1XYEWMRQREVfmcsHnana7nbS0tDyPJSQk0LdvX1q2bMmcOXOIiopi1qxZ/OMf/yhyed7e3nTs2JGoqKgcdYiKispzrJG78dEO7SIi4sIs7eoKDw+ne/fuvPrqq1ZeNttzzz1HREQEQUFBnDt3jm+//Zbly5ezaNGiXOfa7XYiIiIIDg5m1qxZeHl50apVK5YsWUJ4eDiBgYF5tv4kJyezf//+7OeHDh0iOjqa6tWrExQUBEBkZCQjR46kU6dOhIaG8sEHH5CSksKoUaNK5Od2JtqvS0REXJmlwWf9+vV07drVykvmEB8fz4gRIzh+/Dh+fn60a9eORYsWcdNNN+U618PDgzfeeIOePXvi7X15E6qQkBB+++03atWqlWcZmzZtIiwsLPt5ZGQkACNHjmT69OkA3HPPPZw8eZIXXniBEydO0L59e3799ddcA57dUQW1+IiIiAsr9l5dV+rYsSMtWrRgxowZVl2yzHCGvboKYtxC+GkvvNQbRrV3dG1EREQK9x1q6Rifxx9/nPnz57Nz504rLytOxEddXSIi4sIs7epq1KgRffr0oWvXrjzyyCN07twZf3//PKeP9+rVy8qipZSoq0tERFyZpcGnT58+2Gw2DMPgvffeu+Z6OVduIyGuQys3i4iIK7M0+LzwwgulsjigOI5mdYmIiCuzNPi89NJLVl5OnFD2ys1q8RERERfk8gsYSunKWrlZwUdERFxRiezVlZKSwrx584iOjiYpKQlfX1/at2/P4MGDqVSpUkkUKaVEg5tFRMSVWR58fvjhB8aMGcPZs2e5cokgm81G1apV+fzzz7njjjusLlZKSeVLa0GeveDYeoiIiBSFpcFnzZo13HvvvXh6evLQQw8RFhZG3bp1OXHiBMuWLePLL7/k3nvvZcWKFWViXyt31KCqeX/orCNrISIiUjSWrtw8YMAAli9fzurVqwkJCcl1/M8//+TGG28kLCyMn376yapi3YKrrNx8/iK0+Nh8vHUMVK/g2PqIiIg4bOXmtWvXcs899+QZegDatWvH3XffzZo1a6wsVkpRhXJQr4r5+MBpx9ZFRESksCwNPqmpqdfdqNPf35/U1FQri5VS1ri6eb//jGPrISIiUliWBp8GDRqwZMmSa54TFRVFgwYNrCxWSlmTaub9frX4iIiIi7E0+Nx9991s3ryZkSNHEhsbm+PY8ePH+dvf/sbmzZu55557rCxWSllWi88BtfiIiIiLsXRwc2pqKmFhYWzcuBFvb2+aNGmCv78/cXFx7N+/n/T0dEJDQ1m2bBkVKmhU7JVcZXAzwLpjcM8PEOQHv//N0bUREZGyzmGDmytWrMjKlSt56aWXqFevHjt37mTZsmXs3LmTevXq8fLLL7NixQqFHhfX+FJX19FEreAsIiKuxdIWn6udO3cue+XmKlWqlFQxbsGVWnwMA0I+g8Q0+HUYtKzl6BqJiEhZ5rAWH09PT4YPH579vEqVKgQGBir0uBmbTeN8RETENVkafHx9falfv76VlxQnldXdpeAjIiKuxNLgExoayh9//GHlJcVJaUq7iIi4IkuDz0svvcTSpUv56quvrLysOKEmWsRQRERckKWblC5ZsoQ+ffowatQoPvzwQzp37oy/vz82my3HeTabjQkTJlhZtJSyrK6ug2fAboCH7drni4iIOANLZ3V5eBSsAclms5GZmWlVsW7BlWZ1AWTYocVkuGiH1aOgnvNXWURE3FRhvkMtbfFZtmyZlZcTJ+blAQ2qwr7T5jgfBR8REXEFlgYfm82Gr68v7du3t/Ky4qSaVDeDz4Ez0KeBo2sjIiJyfZYObg4LC+P//u//rLykOLHsKe2a2SUiIi7C0uBTu3ZtfHx8rLykOLHGmtklIiIuxtLgc9NNN7F8+XJKcBcMcSJN1OIjIiIuxtLg89Zbb3Hq1CnGjBnD6dP6NnR3WV1dCefh7AXH1kVERKQgLB3cfP/991O1alWmTp3KN998Q8OGDfNdxycqKsrKosUBKnlD3cpwPNkc4NyxrqNrJCIicm2WBp/ly5dnP05LS2P37t3s3r0713lXByFxXY2rmcFn/2kFHxERcX6WdnXZ7fYC3bR4ofvQLu0iIuJKLA0+UvZogLOIiLiSUg8+6enpJCUllXaxUkKyp7Qr+IiIiAsodvBp1KgRkyZNyvHaokWLiIyMzPP8N998k2rVqhW3WHESWTO7jiTBRfVgioiIkyt28Dl8+DBnz57N8dq6deuYOHFicS8tLqB2JfD2NHdoP5Hi6NqIiIhcm8b4SLF42KBOZfPx8XOOrYuIiMj1KPhIsQVUMe9jFXxERMTJKfhIsQVcavFR8BEREWen4CPFlt3ik+zYeoiIiFyPgo8Um7q6RETEVViyZcU333zDunXrsp/v378fgFtvvTXXuVnHxH1kBR8NbhYREWdnSfDZv39/noHm119/zfN87dXlXrLG+MQo+IiIiJMrdvA5dOiQFfUQF1b3UotPYhqkpJu7touIiDijYgef4OBgK+ohLsy3PFTxhnPp5gDnptUdXSMREZG8aXCzWKKuxvmIiIgLUPARS2gtHxERcQUKPmIJTWkXERFXoOAjltAihiIi4goUfMQSavERERFXoOAjltAihiIi4goUfMQSVy5iaBiOrYuIiEh+LFm5OS8pKSmcPXuWzMzMPI8HBQWVVNHiAHUuBZ+0TDhzAapXcGx9RERE8mJ58JkyZQrvvfcee/bsyfccm81GRkaG1UWLA5X3gloV4WSq2eqj4CMiIs7I0uDzySefMHbsWLy8vOjVqxf16tXDy6vEGpXEyQRUMYPP8XPQtrajayMiIpKbpankgw8+oGbNmqxatYpmzZpZeWlxAXUrwx9x2qxUREScl6WDm//66y/uvvtuhZ4yKntml9byERERJ2Vp8Klbt26+g5nF/WlKu4iIODtLg8/IkSNZuHAhKSkpVl5WXERW8FFXl4iIOCtLg8+///1vOnfuzE033cTKlStJTlafR1miFh8REXF2lg5uLl++PACGYRAWFpbveZrO7p6yFjE8kQIZdvDS8pgiIuJkLA0+PXv2xGazWXlJcSG1KkE5D7hoh/iUyy1AIiIizsLS4LN8+XIrLycuxsMG/pXhWJI5zkfBR0REnI06I8RSgRrnIyIiTqzEllWOiYkhOjqapKQkfH19ad++PYGBgSVVnDiJupfG+cQq+IiIiBOyPPjs37+fxx57jKVLl+Y61rdvXz7++GOaNGlidbHiJLJafGI1oU9ERJyQpcHn6NGj9OjRg/j4eFq0aEGvXr2oW7cuJ06cYOXKlfz222/07NmTDRs2UL9+fSuLFidRNyv4qMVHRESckKXB5+WXXyY+Pp6PP/6YRx55JNcMr88++4zHHnuMV155hc8//9zKosVJBCj4iIiIE7M0+CxatIiBAwfy6KOP5nn8kUce4ZdffmHhwoVWFitOJGstH+3XJSIizsjSWV3x8fG0adPmmue0adOGkydPWlmsOJEAX/P+9Hk4f9GxdREREbmapcGnVq1a7Ny585rn7Ny5k1q1allZrDgRX2+oVM58rFYfERFxNpYGn/79+/Pjjz8yZcqUPI9PnTqVn376iVtuucXKYsWJ2GyXx/kcSXRsXURERK5mMwzDsOpiR44coVOnTpw6dYpWrVrRu3dv/P39iYuLY+XKlezYsYOaNWuyadMmzeq6SlJSEn5+fiQmJuLr6+vo6hTLE7/CvD3wZBcY39XRtREREXdXmO9QSwc3BwUFsXr1ah555BGWL1/Ojh07chwPCwvjk08+Uehxc50DzOCzMdbRNREREcnJ8gUMmzZtytKlSzl69GiulZvLUuBZsGABTz31FHa7nWeeeYaHHnrI0VUqNZ0DzPutJ+BiJpTzdGx9REREspTYlhX169cvU0HnShkZGURGRrJs2TL8/Pzo2LEjQ4YMoUaNGo6uWqloWgN8y0NSGuxKgHb+jq6RiIiISZuUloANGzbQunVrAgMDqVy5MhERESxevNjR1So1HjboVNd8rO4uERFxJsVq8Rk9ejQ2m4033ngDf39/Ro8eXaD32Wy2fGd+Xcubb77JnDlz2L17NxUqVODGG2/k7bffpnnz5oW+Vn5WrlzJO++8w+bNmzl+/Dhz585l8ODBuc6bPHky77zzDidOnCAkJIQPP/yQ0NBQAGJjY3NsyBoYGEhMTIxldXQFnQNg6WEz+DzYwdG1ERERMRUr+EyfPh2bzcYzzzyDv78/06dPL9D7ihp8VqxYwdixY+ncuTMZGRk8//zz3HzzzezcuZNKlSrlOn/16tWEhoZSrly5HK/v3LmTGjVq4O+fuw8mJSWFkJAQRo8ezR133JFnPWbNmkVkZCSffvopXbp04YMPPqB///7s2bOH2rVrF/rnckdZ43w2xYJhmNPcRUREHK1YwefQoUMA2a0bWc9Lyq+//prj+fTp06lduzabN2+mV69eOY7Z7XbGjh1L06ZNmTlzJp6e5gjbPXv2EB4eTmRkJE8//XSuMiIiIoiIiLhmPd5//30efvhhRo0aBcCnn37Kzz//zNSpU3n22WcJCAjI0cITExOT3RpUVrT1B29POJkKfyVCg6qOrpGIiEgxg09wcPA1n5e0xERzhbzq1avnOubh4cEvv/xCr169GDFiBF9//TWHDh0iPDycwYMH5xl6CiI9PZ3Nmzfz3HPP5SirX79+rF27FoDQ0FC2b99OTEwMfn5+LFy4kAkTJuR5vcmTJzN58mQyMzOLVB9n5eMF7WrDpuOwIUbBR0REnIOlg5tfeeUVVq5cec1zfv/9d1555ZVil2W323nyySfp3r17vvuDBQQEsHTpUlatWsWwYcMIDw+nX79+fPLJJ0UuNyEhgczMzFzdZP7+/pw4cQIALy8v3nvvPcLCwmjfvj1PPfVUvjO6xo4dy86dO9m4cWOR6+SsQi8Nc9IAZxERcRaWBp+XXnqJ5cuXX/OclStX8vLLLxe7rLFjx7J9+3Zmzpx5zfOCgoL4+uuvmTVrFl5eXkyZMgVbKQw4GTRoEHv37mX//v2MGTOmxMtzRp2uGOcjIiLiDEp9Ont6enr2eJuiGjduHAsWLGDZsmXUq1fvmufGxcUxZswYBg4cSGpqKuPHjy9W2TVr1sTT05O4uLhc5dSpU6dY13Y3WVPaD56FhFSHVkVERAQogeBzrdaU9PR0fv/99yLPfDIMg3HjxjF37lyWLl1Kw4YNr3l+QkICffv2pWXLlsyZM4eoqChmzZrFP/7xjyKVD+Dt7U3Hjh2JiorKfs1utxMVFUW3bt2KfF135OcDzS/18KnVR0REnEGxV25u1KhRjuf//e9/mTZtWq7zMjMzSUhI4MKFCzz88MNFKmvs2LF8++23zJ8/nypVqmSPqfHz86NChQo5zrXb7URERBAcHJzdzdWqVSuWLFlCeHg4gYGBebb+JCcns3///uznhw4dIjo6murVqxMUFARAZGQkI0eOpFOnToSGhvLBBx+QkpKSPctLLuscAHtOmeN8bmni6NqIiEhZV+zd2Rs0aJDdynPkyBF8fX2pWrVqrvM8PT2pXr064eHhTJgwIc91d65b2Xxak6ZNm8bf/va3XK8vWbKEnj174uPjk+P1rVu3UqtWrTy7yZYvX05YWFiu10eOHJljnaKPPvooewHD9u3bM2nSJLp06VK4H+gK7rQ7+5Xm7oYnF0F7f5h/r6NrIyIi7qgw36HFDj5X8vDw4KWXXuKFF16w6pJlhrsGn2NJ0H0aeHnAtkehYrnrv0dERKQwCvMdaukmpYcOHcqztUfKrsAqULcyHE82d2vvXjb3rRURESdh6eDm4OBg/Pz8rLykuDibLef2FSIiIo5kaYtPlrVr1/Lbb78RGxtLWlparuNF3atLXFOHOvDjXtgW7+iaiIhIWWdp8MnIyOC+++5jzpw5GIaBzWbjyiFEWc8VfMqWNpdWL9iu4CMiIg5maVfXe++9xw8//MCoUaPYtGkThmHw5JNPsnbtWt5++22qVq3KXXfdxYEDB6wsVpxcy5rm/fFkOKWFDEVExIEsDT4zZsygTZs2fPHFF9xwww0AVK1alS5duvDPf/6TlStXsmDBAhYtWmRlseLkqpSHhlXNxztOOrQqIiJSxlkafPbv30+fPn2yn9tsNi5evJj9vHXr1gwcOLBYm4SKa1J3l4iIOANLg4+3tzcVK1bMfl65cmXi43N+0wUHB7Nv3z4rixUX0KaWeb9dLT4iIuJAlgaf+vXrc/To0eznLVq0YOXKlTkGOK9bt47q1atbWay4gNaXgs8OtfiIiIgDWRp8evfunSPo3HPPPezZs4cBAwYwefJk7rvvPlatWsUtt9xiZbHiAlpf6uo6nAhJuVc4EBERKRWWTmcfPXo0mZmZxMTEUK9ePR5//HGWL1/OggULWLhwIQChoaG89dZbVhYrLqB6BXMV55hzsPMkdM29TZqIiEiJszT43HDDDTkGLpcrV44ff/yRTZs2ceDAAYKDgwkNDcXDw9KGJnERbWqbwWd7vIKPiIg4Roms3Hy1Tp060alTp9IoSpxY61qw6ICmtIuIiOOo6UVKjWZ2iYiIoxWrxSc8PLxI77PZbERFRRWnaHFBWWv57D8N5y9ChXKOrY+IiJQ9xQo+y5cvz/P1q/fouvp1m81WnGLFRdWuBLUqwslU2H3K3LxURESkNBWrq8tut+e4nT9/ngEDBtCsWTO+/vprDh8+zPnz5zl8+DBfffUVzZo1Y+DAgaSmasOmsshmg1ZZ3V1az0dERBzA0jE+L774Itu2bWPjxo0MHz6coKAgypcvT1BQEPfffz/r16/njz/+4MUXX7SyWHEh2rpCREQcydLg8+233zJ06FAqV66c53FfX1+GDh3K//73PyuLFReiAc4iIuJIlgafkydP5tiUNC8ZGRm59u+SsiOrxWfvKUjPdGxdRESk7LE0+DRu3Jjvv/+eU6dO5Xn85MmTfPfddzRp0sTKYsWF1PcF3/Jm6Nl32tG1ERGRssbS4PPkk09y4sQJbrjhBiZOnMjmzZs5evQomzdv5oMPPqBjx47Ex8czfvx4K4sVF2KzXd6wVON8RESktFm6cvNDDz3E8ePHefXVV4mMjMxxzDAMPD09eemllxg9erSVxYqLaVMb1h4zg889rR1dGxERKUss37JiwoQJDBs2jBkzZvDnn3+SmJiIn58fISEhDBs2jMaNG1tdpLiYrAHO0SccWw8RESl7SmSvrsaNG/PCCy+UxKXFDXSrDx42+DMeDp6BRtUcXSMRESkrtFeXlDr/StA72Hw8e6dj6yIiImVLsVp8Vq5cCUBoaCg+Pj7ZzwuiV69exSlaXNzdrWDZYZi9C57qBp6K4CIiUgqKFXz69OmDzWZj165dNGvWLPt5QWRmahGXsqxfI6jmA3EpsPIIhDVwdI1ERKQsKFbweeGFF7DZbNSsWTPHc5Hr8faEIS1gajR8t0PBR0RESofNyGsbdSl1SUlJ+Pn5kZiYiK+vr6OrUyp2noSIb6GcB2x4CKpXcHSNRETEFRXmO1QjK8RhWtUy1/S5aIf5exxdGxERKQsUfMSh7mpl3n+n2V0iIlIKijXGJzw8vEjvs9lsREVFFadocRODm8Prv5vdXtvjL29iKiIiUhKKFXyWL19epPdpALRkqeoDNzeCBfvg+50KPiIiUrKK1dVlt9uLdNNUdrnS3Zf265q729y1XUREpKRojI84XI/64FseEtNg32lH10ZERNyZgo84nKcHtKhhPt6T4Ni6iIiIeyuRTUovXLjAxo0biY2NJS0tLc9zRowYURJFi4tqXhM2xMLuU46uiYiIuDPLg8/kyZOZMGECiYmJeR43DAObzabgIzlktfjsVouPiIiUIEu7uubMmcPjjz9O/fr1effddzEMg9tvv5033niDW265BcMwGDp0KFOnTrWyWHEDzc1dT9ijFh8RESlBlgafDz74gNq1a7N27VrGjx8PQPv27XnmmWf4+eef+eabb5g3bx7BwcFWFituoPmlFp8TyZB4wbF1ERER92Vp8Pnzzz8ZNGgQFStWzH7tyqnrw4YNIzw8nFdeecXKYsUN+JaHelXMxxrnIyIiJcXS4HPx4kVq1aqV/bxChQqcPXs2xzkhISFs2bLFymLFTWR1d+3SOB8RESkhlgafgIAAjh8/nv08ODiYrVu35jjnr7/+wsurRCaTiYvTlHYRESlplgafzp0752jNueWWW1i9ejVvvvkmO3bs4LPPPmPOnDl07tzZymLFTWS1+KirS0RESoqlweeuu+4iLS2Nw4cPA/Dcc89Rr149/v3vf9OuXTsee+wxKleuzH/+8x8rixU3kdXis/cUGIZj6yIiIu7JZhjF+4qZOXMmd9xxB97e3nkeP3PmDF988QUHDx4kODiYBx54gMDAwOIU6ZaSkpLw8/MjMTERX19fR1fHIS5mQsuP4aIdVo2C+mXzYxARkUIqzHdosYOPh4cH1atXZ/jw4YwePZqQkJDiXK7MUvAx9f/G7OqaMhD6NXJ0bURExBUU5ju02F1d9913H+fPn+fDDz/khhtuoHPnznz66af5rtwsci0tssb5aICziIiUgGIHnxkzZnD8+HEmT57MDTfcwObNmxk7diwBAQE88MADLF++3IJqSlnRQis4i4hICbJkcLOvry+PPfYYGzduZNu2bTzxxBNUrlyZGTNm0LdvX5o0acIbb7xBTEyMFcWJG8tawVlr+YiISEmwdFYXQOvWrXn//feJiYlh9uzZRERE8Ndff/Hvf/+bBg0acNtttzFnzhyrixU3kdXic/AMpGU4ti4iIuJ+ij24uSBOnDjBV199xdSpU9m7dy8eHh5kZOhb7Uoa3GwyDGj3KSSlw8Jh0KrW9d8jIiJlW6kObi6IM2fOEB8fn719RSlkLXFRNpsWMhQRkZJTYntHJCcn87///Y+pU6eyYcMGDMOgYsWKjBgxggcffLCkihU30LwGbIzV1hUiImI9y4PPihUrmDp1Kj/88APnz5/HMAw6d+7Mgw8+yH333UeVKlWsLlLcjKa0i4hISbEk+MTExDB9+nSmT5/OwYMHMQyDGjVq8PDDD/Pggw/Spk0bK4qRMkJT2kVEpKQUO/hERETw22+/kZmZic1mo1+/fjz44IMMHjw4320sRK4la0r78WRIvAB+Po6tj4iIuI9iB59FixYRFBTEqFGjGDVqFEFBQVbUS8ow3/IQWAVizpkDnLtoazcREbGIJcGnX79+2Gw2K+ojAkDb2mbwWbRfwUdERKxT7OnsN910k0KPWG5YW/N+1k44l+bYuoiIiPsolXV8RAqrVxA0qQ7J6TBrh6NrIyIi7kLBR5ySzQYPtjcfT/sDMu0OrY6IiLgJBR9xWne0hGo+cCwJFh90dG1ERMQdKPiI0/LxujzWZ8pWx9ZFRETcQ4ltWSFihZHt4LPN5hYWf8ZBO//8zz19HnYlQFKaOSA66dKg6FubQoAWDBeRMmR3Ajy8AIa3gUc7Obo2zsXS4DNr1izuuOMOypUrZ+VlpQzzrwwDmsK8PWarz8Rbcp+zPR6mRcOPeyE9M/fxN1fDwGYw5gbt9i4iZcMnm+BIovn7r3oFuLu1o2vkPGyGhVule3h4ULNmTUaMGMFDDz1EixYtrLq020tKSsLPz4/ExER8fX0dXR2nsi0OBswELw+YfRcYBpy9AHEpMGcXbIi9fG6wH9SsCFW8zYUQTyTnPN4zCJ7voQAkIu7r7AUI/QLSLv0h6OUBX94OPdx4feHCfIdaGnxeeOEFpk+fzrFjx7DZbHTv3p2HH36Yu+66Cx8f7TtwLQo+13bn92Z3V168PODWJjC6A3Sok/v4n3Hwf1vg531gN6CyN0wbBKFaGFFE3NDUrfDySmhVE5rWgPl7zD8Gf7gLmtd0dO1KhsOCD4DdbmfhwoV88cUX/Pzzz2RmZuLr68v999/PQw89REhIiJXFuQ0Fn2tbcxQe/Ak8bFDVx7xV8zGDzvC2UKfy9a9xNAn+sQTWHTMHTv/fAOgdXPJ1FxEpLYYBN8+Avafg1T5wT2u4f67Z8h1YBebeA/6VHF1L6zk0+FwpPj6eadOmMWXKFPbv34/NZqNjx46MGTOGe++9l8qVC/BtVUYo+FyfYZjr+xTHhQx49GdYdhi8PeHDW+CWJpZUT0TE4TYfhzu+M/+42/iQ2eV/5jwM+Q4OnQUbUMkbKpaDSuWgWgVoUQNa1DRbiFrUhCrlHf1TFJ7TBJ8rLVmyhFGjRnH8+HEAKlWqxP33388zzzxDcLD+7FbwKT3pmfDEr/DLfvC0wXs3wxANRxMRN/CPJfD9Trizpfm7Lcvhs2bLz9Gk61+jcTWzNb1DHehQF1rWNFvbnZlTBZ+dO3fy+eef880333Dq1CkqVarEkCFDiI6OZvv27VSoUIHZs2cTERFRktVwego+pSvDDs/8BrN3meHn2zugaz1H10pEpOiS0qDzF2bL9uy7oHNAzuMZdnPZj9SLkHIRUtPheLI59X3Xpdvx5NzXbeBnjqG8q5XZUuSMHB58zp8/z8yZM/n8889Zv349hmHQrl07HnnkEe6//36qVDEXVVm4cCF/+9vf8Pf3588//7S6Gi5Fwaf02Q2z5efHvVCjAvx0LwTqoxcRF/X1n/DvZdC0Oiy5v2hDA06lQnQcbD0BW4+b9ykXzWN+5c0xlSPaQV0nWxvNYcFn06ZNfPHFF8ycOZNz587h4+PD3XffzaOPPkqXLl3yfM/zzz/Pu+++S3p6ulXVcEkKPo5x/iLc8T3sPAlta5t/JfloWU8Rycfp8+bvjYAqxR9zaLVbv4UdJ+GFXvBgB2uumXrR7DqbshX+SjRf87BB9/pwRwvo39gcM+RohfkOtfRXfGhoKACtWrXikUceYcSIEfj5+V3zPUFBQQQGal6xOEaFcubsroH/g23x8PxSeO8m5/uFVhDfbjOn/L/ZV+FNpCScTIG+X0NiGtSqaI6BaX9pLEyIv2MDwJbjZujx9jQDiVUqloORIXB/W/jtkBmA1sfA70fMW8VyMKgZTOhlLhXiCixt8XnggQd45JFH6NGjh1WXLDPU4uNYq4/CA3Mh04CXesOo9o6uUeF1+hxOpsJHEeZK1SJirffWwqQNeR/zsEHzGpfDUKNqEOQLtSpdHhhsGGa3UUIqnDoPiRfgbJp5n5ZhzqbyvXSr4g3lPMHLBp4e5u30eYg9d/kWk3WfBEmXOk0GNYMPS3jI7F9nYe5umLP7civQoGYw6RbH/dHo8DE+UngKPo73xRZ49XdzsPPMoa61wGFaBjSbbD4e2hLev/na54tI4Zy/CF2nmqsi//dmqO8H0SfMMTDRJ8wQkpfynlDP15xNmpAK5zNKro51K8OUQdC6lFamNwxYehjGLDAHTr8WBg+0K52yr+awri4RV/ZgB/gz3lzldNxC+GWYuf2FKzhxxUyMFYfNgdvOPv1UxJV8t9MMPfV94fbmZgvMlbOm4pIvDQg+Ya4WfyTJbI1Jy4QDZ3Jeq1I5c/8sPx+oWt689/GC5HSzGy1ro+UMu3nLNCAj0zwvoMoVt8rmhIzAKuattLvabDbo2xCe7Q6v/Q6vrIT2/tD2GptJOwNLg0+jRo2ue46Hhwe+vr40b96cIUOGcPfdd1tZBZEis9ngzXCzn3z/afj7r/D1YPMXnLOLvSL4JJyHHfHO/8tHxFVk2uGLrebjh27I+3eCf2VzMdQrF0S9mGmGn6NJZrCpXcn8Y8pZp4QX1UMdYEMMLD4Ij/0CPw8zZ4A5K0t/pdvtdtLT0zl8+DCHDx/m2LFjXLhwgWPHjmW/duHCBfbv38+sWbO47777uPnmm8v8jC5xHpW84ZNboYKXOe5n4npH16hgjl/VzL7sL8fUQ8QdLTpg7nRe1QfublXw95XzhOCq5uagnQIgyM/9Qg+YfzS+e5PZGnY0Cf65xOwGc1aWBp/o6Gjq1q1LeHg4a9asIS0tjdjYWNLS0lizZg19+/YlICCAI0eOsHfvXm699VaioqJ47733rKyGSLE0q2HOjAJzIONKFwgRsZeCT9ZsruWHHVYVEbdiGOYmx2COX3HH4GIFPx/4+FZzVtmiA2bXoLOyNPg888wzpKWlsXjxYrp27Yrt0vBum81G165d+fXXX7lw4QLPPvssTZo04fvvvyc4OJiZM2daWQ2RYhvSAoa3AQN4YlHuFhVnk7Xa6sCm5v3WE+Z4BBEpnk2x5v9P5T1hpIMG7rqKdv7wWEfz8bLDDq3KNVkafObPn8+tt96Kh0fel/X09OTWW29l/vz5APj4+BAeHs7+/futrIaIJV7oDW1qm1NIP9/i6NpcW1aLT8cAs8XKbrhGS5WIs8tq7bmjpTk1Xa4ta8D3ngTH1uNaLA0+SUlJJCVdewe0xMREEhMTs5/XrFnTyiqIWMbHCx7vbD5eetihVbmurOBTtzL0ubTn73IFH5FCsRvmWJ7fDsLHG+HJRbDkoHnsIYtWQnZ3zS99pR9ONPcMc0aWzupq1aoV//vf//jHP/6R5wyvgwcPMnPmTFq1ujw67MiRI9SqVUqLDogUUo8gKOcBh87CoTPQsJqja5S3rFldAVWgTwPzr1RNaxfJm2GYfyzsOQV7T8He0+b9/tN5r7NzS2NoUr306+mKalU0p+qfPg/7Tjnn7FJLg8/zzz/PnXfeSfv27XnooYfo3r07tWvXJj4+ntWrVzNlyhSSk5N5/vnnAUhPT2fx4sXcfLNWWxPnVNnbXMhw9VGzz9oZg09KurnuB5gtPg2qmuuEaFq7iLkezpW7j+++FHaS85lM7O0JjauZG302q2GuxtwzqHTr7Mpsl1awXnvM/Kyd8fePpcHnjjvu4IsvvuDJJ5/kgw8+YOLEidnHDMOgcuXKfPbZZ9xxxx0ApKamMmXKFFq3bm1lNUQsFdbADD5LD8NoJ2zuzmrtqeJtLnkPZkvVogPmtHZn/MUjUhJOn4ft8ea+e9vjYftJs+sqL14eZsBpVuNyyGlWA4L9zGNSdNnBx0nH+Vi+cvPo0aMZOnQo8+fP548//iApKQlfX19CQkK4/fbbc2xaWrVqVW6//XarqyBiqfCG5qqk62PM1hVn2In4SlkzzgKqXH6tT/Cl4HMY/h7qkGqJlKgLGWbAiT4Bf8SZM6+O5TPEtE5laFkTWtWEFpduDaqarTtivRaXxvnsPeXYeuTH0uDzyiuv0LBhQx544AFGjBhh5aVFHKZRVXPhsSOJZsvPzY0dXaOcrhzYnKVPA/M++tK09qo+pV4tEUudS4PNx80VgtfHmNvLpGfmPq9RVXM2Zpva5p5VrWtBtQqlXt0yrXkN8353WQg+r732Gk8++aSVlxRxOJsNwhvA9D/M7i5nCz7HrxjYnCWgivnLZ88pWPGXubeQiKtJSjNnVS3YC78fgYv2nMdrVby8G3qIv7mOjK8Tb5VQVjS7FHziU+DMeecLnpYGn6CgIM6ePWvlJUWcQlgDM/gsO2zOCLE50Uyp7BafKjlfv6mRGXxmbFPwEdeyMRY+22yG9itbder7QtdAc8JBl0CzJdaZ/l8UU2Xvy9tX7D4F3eo5ukY5WRp87r33Xr766isSExNzjOURcXVd65nr+pxINmeGtHKiFRiygk9A5ZyvP9DO/PJYH2N2ebWvU/p1EymM/afhP2vM8WlZmlQ3VyS/tenllgRxfs1rXAo+Cc4XfCwduz5hwgTatWtHeHg4P//8M/Hx8VZeXsRhfLyge33zsbMtxZ7V1XV1i0+dypdbej7bXLp1EimM0+fhX0vh5m/M0ONhg/vawOLh8Nv98GRXhR5X09yJBzhb2uJTsWJFwJy6PmjQoHzPs9lsZGQ46ZKOIvkIbwBRh2DpIRjb2dG1MWUtxAa5W3wAxtwAs3fBrwfgr7PmTtEizsRuwMh55mBlMLton+luTjEX19XCiQc4Wxp8evbsmb0xqYi7CWtg3m9xoplSiWmXV5q9usUHzL+6+gSb21d8vhVeCyvd+olcz497zNBTxRumDDLH7ojru3JKu7ONi7Q0+CxfvtzKy4k4lUBf55spldXaU6OC2R2Xl0c6msHn+50wvgvUqFh69cuSetFcM0ULw8mV0jLgnbXm40c7KvS4k4ZVze1+ktPh2DlzsLOzsHwBQxF3FtbADD6zdsDNjaBCOcfW53g+M7qu1K0etKtt/lX91Z8wvmvp1A3g8Fl4by38uNcct1GrojnVPmtrjabVoWkNaFLN8Z9lQdkN8157oBXft9vNRQdrV3LOVdGl6Mp5mgPTdyWYO7W7ffBJT0/nt99+Y/fu3aSkpDBhwgQALly4QFJSEjVr1sTDQ3/6iesZ2MzcAHT1UbjtfzCxv2O3hMjenDSP8T1ZbDaz1WfsQvjyD/Mv65IOGXHJMGkDzNwBGZfWXrEbEJdi3rZeXUegnq85PTnID4J8zTBXzuPyzwBQwcvsEqnkbU6ZrVGhdFfSjj0Hg2aa68l0q2cOeO9R3wxxztSU7wrOpZn/jYDZElnRRYKvFFyzGpeCzynol3vfcoexPPj8+OOPjBkzhpMnT2IYBjabLTv4/Pnnn3Tr1o2vv/6aYcOGWV20SIlrUxu+uh2eWgIHzsDg78xf2o91Ak8HZPmCtPgA3NLk8roa3++EESFFK89uwEcbzUXi7m2du3stMQ0+2wRTos0tBcBsJftHN/Ov+uPnzFlosefMz2//aXNn7NPnzbodTTJDZWFU8zFDU2AVc/B2m1rQtrb52OpWmUkb4GSq+XjhfvMG5mrBYzvD4Bbqziuo/9ti/rs3qgp3a7tGt9SiBszH+fbsshmGYVh1sdWrVxMWFkbdunX55z//ybp16/jf//5HZublFaiaN29OmzZt+OGHH6wq1i0kJSXh5+dHYmIivr5O1CYoeTpzHp5fCr9c+uLrVBc+uKX0m3Of+BXm7YHnusOjna597vQ/4MXlZt/70hFFCwUr/oIR88zHtSrC/+sEw9qaLTZf/wkfbjQHfgN0rGvOzinIuI2EVDh0Bo4kmVuDHEk0A5JhQNYvKLthDuROSTfHDZxLvxyu8lLFG1rXhm6B5qatIf5m83tR/XUWwr6CTAPe6msGoNVHYcvxy4vsNaoKT3QxWwYdEYRdRXwK9Jpu/nt+ehtENHF0jaQkRB2C0T+aYyMX31+yZRXmO9TSFp9XX32VqlWrsnnzZmrWrMmpU7nnsXXq1In169dbWaxIqatWAT6+FebshheWw6bjEDHDnDU1uEXp1SO/NXzycldLeHcNHDprLv/fO7jw5e08efnxyVR4eSV8shm8PcwBjGD26z9zozktuaDdPzUrmrfOhRzcmpQGMUkQc85sLdp/GnacNOt5Lh3WHTNv/11vdo11q2cuS3BzY7O8wpi4wQw9vYPNNWbA3AA2Jd0MfZ9uhoNn4YlFZqvYP280x4GpCyyn5HR4e7UZejrUgVucbAsYsU7WlPYDZ8w/DpxlU1hLg8/69eu58847qVmzZr7n1K9fn/nz51tZrIhD2GwwtCV0DjC/7LYcN++X/wWv9oEqpbBnUPYaPgUIPpW84a5WMDUapkcXLfjsutRkPb6L2XX10UYzdAD4V4LIrnBnq9Lr7vEtD761oOVVK2ln2M0QtPUErDpitsycuWDu+7TkIPxrmdkSdWsTsxuwdqVrl7PvNMzdbT5+6qrB4ZW8zda2+9vBtGizC2ffaRizwGz1eq6H+d9IWXUhwwyjq46Yty0nLo/7era7gqE7C6hitryeS4eDZy5PcXc0S4NPWlradZuYzp49q4HN4laC/OD7O+GjDWarwNzdsCkW3u53ebXnkmA3zC004NqDm680op0ZfJYdLtqChll99W39oW9DM+TM3W1OV7+3tfPMzPLyMH/Jtqhpts7YDfPLd+Vf5ricbfGw9ph5e2mFuZv9nS3NAZh5/VX6wTrzGjc3gpB8tv6o7A2Ph5rjpz7bDFO2mruJ3/m9+b6nupXuL/7zF80WyXPpkGk3w0amHapXNLs7G1Y1v5isDKlnL5gtivtOwR9x5m13Qu7NRYP8YGQ7cysYcV82mznAefNxc4CzWwafRo0asXHjxmues3btWlq0KMW+AJFS4OVhLqvfI8hs9TmaBMPmwD2t4V89wK8EFjtMSDW/UDxs4F/A4NOwmtnSs+Iv+Hob/LtnwctLzzSbrAFaXvoF5u1p/ozOzsNmDnhuW9schHwk0QxAv+yD6DhzLELUIXOg9OAWMLzt5ZWDd56EBfvMx5EFWArArzw8faP5xf7f9ebSB4sPmrebGsG4zqWzb9qrK2HG9mufU87DHBRet8rlZQb8K5mtWD5e5iw6Hy8z9KVnmv+9pWeaXYwJqXDqPJxKNVv9Dp81W9XyUr0ChAZAzyDzphXEy44WWcEnAXCCtc/A4uAzdOhQXnvtNaZNm8aoUaNyHX/33XfZvn07//nPf6wsVsRpdAqARcPNMQxf/Wl+6S09BK/0MTdZtFLWjK7alQr3V/vIEDP4zNphfpEXdBrxgdNmq4Gvt/kF6cqC/Mwp/o90NLvEZu+EH3abg26nRZu37vXNFrLvd5rvGdgsd5fatfhXNgdBP9gB/rvODFlZXW09g8xlBW6sXzLrAe09Bf/bcbneFbzM/0Y8bObPeOisGf7SMuFwonmzSp3KZmtS29pmwGvnD/WqqEurrMras8uZtq6wdFZXcnIyXbt2ZdeuXYSHh5OWlsbq1at56qmnWLt2LWvWrKF9+/asWbOG8uVLYQCEC9GsLvezMRae+e1yK0m72uY4kEHNrOkSWrgfHv3ZHCA6756Cv89uQO8vzS++t/peHqh7PXN2w/hF5l/u399VtDo7swy72RX2v+3w26HLCxWCGRiW3G8O3C6q/afhk01m12DmpWvX9zVbzO5qZQYGq4yaD0sPQ//G8H8D8j7Hbpjh+WiSuR5U1lID8SnmuJzzF80ByOczwMtmzojz9jTvfb3NFcBrVDAHideuZIadBlW1Ho/ktD4G7p5tdsevfbDkyinMd6ilwQfgzJkzjBs3ju+++y7HNHabzcbdd9/Nxx9/TLVq1aws0i0o+LinCxnmAODPNl+e8uzrDUNbQa8g88uuTmWzi6WwfxFP3WrOqrqtqTnDrDA+3wKv/W52WS0cVrCy31hl/hwj2sGrbr7n17EkmLHNDEFnLsDdreCdm6y59tEk8/Ofs8scfwNmsOoVZA60Dm9odjcV1aojMHyu2cKz5H5opF+34kDn0qDNp+bjLQ+X3JY5Dg0+WU6dOsXGjRs5ffo0vr6+dO7cGX9/By5x6+QUfNxbQqrZnTJju9nScjVvT/Ov/w514Ia65n3zGtdeC+bVlfDFVnioA0zoVbj6JF6ALlPMv+a/u7Nga+2MmGd2kb0Zbq7dUxZcyDAHQrcv5hpAeTl/0VwHauZ22BCb81jIpcHjN9Y3WwrLF3BQgt0wVxTfedLs0nylj7V1FimKsC/NpR6+vN2cSFASHLaOz5Vq1KjBLbfcUlKXF3EpNSuaU57HdDT/Iv9+J+w/A/HJkHD+8sDhA2dg9i7zPRXLmbMgWtWEVrXMW7val8NQ1ho+BZnKfjU/HxjSwtwr6cs/ChZ8smZ0NXeSmRmlwcer5KaiVyhnLocwtKX57/7zPog6aA62zpoR9f46KO8JHepClwDzPsTfHCycl7m7zdBTxRueCC2ZeosUVpvaZvDZFl9ywacwtEmpSCnysEGvYPOWJT3THFex95S5xsmW4xB9AlIumo+3HL98bog/vHuTOUW0MGv45GVkiBl8ft1v7p91re6V0+fNc8BsiRJrNa5mLob491Dzc156CJYfNseJnTp/eSHGLPV9zf8W2tY2B1y3rGmGnXfWmMfHdS65LgWRwmrnb25UvC3e0TUxWR58du7cyUcffcTGjRs5e/ZsjnE+WWw2GwcOHLC6aBGX5O1p7jVVz9cc3wHmeisHzpgLBu68tBLx5uNmK8Bt/zMXEMxaOLCga/hcrUVNc4G9zcfNbrixnfM/N6u1J8jPXK9GSo5/JXPA+X1tzC07DpyBDTFmd9gfJ8y/nLP2NcuaZg/mv0tyujk9/W/tHVV7kdza1jbvt7tj8FmxYgW33HILaWlpeHl54e/vj5dX7iJKaFiRiNvw9DBbdZrVgNsvrX1xIhmejTIXH3x7zeVzC7JdRX7ua2MGn5k7zI1W85tavefSVNQWau0pVTabOZOsSfXL46oS02Dbpa6wHSdh10lzenrypYHSz3bPvXmsiCO1vrQMRMw5s/U4v67a0mLp/x7PPvssGRkZfPHFF4wcORJPTyfZmEPEDdSpDNMGmWOAXlkBSelma1Fh95y60m1N4eUV5oDrNUfNBRjzkrVVhbOsvFqW+ZU3/52u/LdKvWh2lV7MLPx+ZyIlrUp5cwPfrHE+Rdkux0qW7h3xxx9/cO+99zJ69GiFHpESYLOZa74secC8/+eNxVsAr2K5yy1Ks3bkf95uBR+nVrGcuVigQo84qzaXurv+jHNsPcDi4FOpUiVq165t5SVFJA91KpuDnMfcUPxrZS1g+OsBsxn6apn2y11dLRV8RKQI2l5azcYZBjhbGnxuvfVWfv/9dysvKSIlrE1t85aeaS6qd7UjieZ6Nj5eEOxX+vUTEdfnTAOcLQ0+77zzDmfPnuXvf/87qampVl5aRErQfZc2Gv3fDnMm0ZWyxvc0q37tBRVFRPJz9QBnR7J0cPO9995L5cqVmTx5MtOnT6dZs2Z5rqBos9mIioqysmgRKYbbm5tbWOw/DZuO51y0T+N7RKS4fMub+7kdOuv4Ac6WBp/ly5dnP05OTmbLli15nmfTNr0iTqVKeRjQzFxReub2q4KPxveIiAXa1r4UfOIcG3wsbbi22+0FuuW1qKGIOFbWIOcF+yAu+fLrZXGrChGxnrMMcFaPvYgAcEMdc4HCCxnQfwb8tBdS0uGvS5uqavFCESkOZxngXOrBJz09naSkpNIuVkSuw2aDj28zN0M9cwHGLYT755nHalfS3k8iUjxZA5yPOXiAc7GDT6NGjZg0aVKO1xYtWkRkZGSe57/55ptUq1atuMWKSAloXA1+vAee7AJeHpc3SFVrj4gUV9YAZ3Bsd1exg8/hw4c5e/ZsjtfWrVvHxIkTi3tpEXGAcp4wvivMu+dy4OkUcO33iIgURFZ31zYHruCsrexEJE9ta8OP95qbYbav4+jaiIg7aFMbftzr2BYfBR8RyVd5LwjV/k8iYhFnGOCsWV0iIiJSKrI2Kz12Ds44aICzWnxERESkVPiWh+Y1zL3/Es5DtQqlXwcFHxERESk1i4aby2c4iiXB55tvvmHdunXZz/fv3w+Yu7VfLeuYiIiIlD2O3rXKZhhX78VcOB4ehR8mZLPZtG3FVZKSkvDz8yMxMTHPjV1FREQkb4X5Di12i8+hQ4eKewkRERGRUlHs4BMc7MAtVkVEREQKQdPZRUREpMxQ8BEREZEyQ8FHREREygwFHwstWLCA5s2b07RpU7744gtHV0dERESuogUMLZKRkUFkZCTLli3Dz8+Pjh07MmTIEGrUqOHoqomIiMglavGxyIYNG2jdujWBgYFUrlyZiIgIFi9e7OhqiYiIyBUUfC5ZuXIlAwcOJCAgAJvNxrx583KdM3nyZBo0aICPjw9dunRhw4YN2cdiY2MJDLy8jXVgYCAxMTGlUXUREREpIAWfS1JSUggJCWHy5Ml5Hp81axaRkZG8+OKLbNmyhZCQEPr37098fHwp11RERESKSsHnkoiICF577TWGDBmS5/H333+fhx9+mFGjRtGqVSs+/fRTKlasyNSpUwEICAjI0cITExNDQEBAvuWlpaWRlJSU4yYiIiIlS4ObCyA9PZ3Nmzfz3HPPZb/m4eFBv379WLt2LQChoaFs376dmJgY/Pz8WLhwIRMmTMj3mm+++SYvv/xyrtcVgERERAon67uzINuPKvgUQEJCApmZmfj7++d43d/fn927dwPg5eXFe++9R1hYGHa7naeffvqaM7qee+45IiMjs5/HxMTQqlUr6tevXzI/hIiIiJs7d+4cfn5+1zxHwcdCgwYNYtCgQQU6t3z58pQvXz77eeXKlTl69ChVqlTBZrNZUp+kpCTq16/P0aNHteO7hfS5Wk+facnQ52o9fabWs+IzNQyDc+fOXXOISRYFnwKoWbMmnp6exMXF5Xg9Li6OOnXqWFKGh4cH9erVs+RaV/P19dX/oCVAn6v19JmWDH2u1tNnar3ifqbXa+nJosHNBeDt7U3Hjh2JiorKfs1utxMVFUW3bt0cWDMREREpDLX4XJKcnMz+/fuznx86dIjo6GiqV69OUFAQkZGRjBw5kk6dOhEaGsoHH3xASkoKo0aNcmCtRUREpDAUfC7ZtGkTYWFh2c+zBh6PHDmS6dOnc88993Dy5EleeOEFTpw4Qfv27fn1119zDXh2JuXLl+fFF1/MMZZIik+fq/X0mZYMfa7W02dqvdL+TG1GQeZ+iYiIiLgBjfERERGRMkPBR0RERMoMBR8REREpMxR8REREpMxQ8HFjkydPpkGDBvj4+NClSxc2bNjg6Cq5jDfffJPOnTtTpUoVateuzeDBg9mzZ0+Ocy5cuMDYsWOpUaMGlStXZujQobkWuZT8vfXWW9hsNp588sns1/SZFk1MTAz3338/NWrUoEKFCrRt25ZNmzZlHzcMgxdeeIG6detSoUIF+vXrx759+xxYY+eWmZnJhAkTaNiwIRUqVKBx48a8+uqrOfaB0md6fStXrmTgwIEEBARgs9mYN29ejuMF+QxPnz7N8OHD8fX1pWrVqjz44IMkJycXq14KPm5q1qxZREZG8uKLL7JlyxZCQkLo378/8fHxjq6aS1ixYgVjx45l3bp1LFmyhIsXL3LzzTeTkpKSfc748eP56aef+P7771mxYgWxsbHccccdDqy169i4cSOfffYZ7dq1y/G6PtPCO3PmDN27d6dcuXIsXLiQnTt38t5771GtWrXsc/7zn/8wadIkPv30U9avX0+lSpXo378/Fy5ccGDNndfbb7/NJ598wkcffcSuXbt4++23+c9//sOHH36YfY4+0+tLSUkhJCSEyZMn53m8IJ/h8OHD2bFjB0uWLGHBggWsXLmSMWPGFK9ihril0NBQY+zYsdnPMzMzjYCAAOPNN990YK1cV3x8vAEYK1asMAzDMM6ePWuUK1fO+P7777PP2bVrlwEYa9eudVQ1XcK5c+eMpk2bGkuWLDF69+5tPPHEE4Zh6DMtqmeeecbo0aNHvsftdrtRp04d45133sl+7ezZs0b58uWN//3vf6VRRZdz2223GaNHj87x2h133GEMHz7cMAx9pkUBGHPnzs1+XpDPcOfOnQZgbNy4MfuchQsXGjabzYiJiSlyXdTi44bS09PZvHkz/fr1y37Nw8ODfv36sXbtWgfWzHUlJiYCUL16dQA2b97MxYsXc3zGLVq0ICgoSJ/xdYwdO5bbbrstx2cH+kyL6scff6RTp07cdddd1K5dmw4dOvD5559nHz906BAnTpzI8bn6+fnRpUsXfa75uPHGG4mKimLv3r0A/PHHH6xatYqIiAhAn6kVCvIZrl27lqpVq9KpU6fsc/r164eHhwfr168vctlaudkNJSQkkJmZmWtVaX9/f3bv3u2gWrkuu93Ok08+Sffu3WnTpg0AJ06cwNvbm6pVq+Y419/fnxMnTjiglq5h5syZbNmyhY0bN+Y6ps+0aA4ePMgnn3xCZGQkzz//PBs3buTvf/873t7ejBw5Mvuzy+v3gT7XvD377LMkJSXRokULPD09yczM5PXXX2f48OEA+kwtUJDP8MSJE9SuXTvHcS8vL6pXr16sz1nBR+Q6xo4dy/bt21m1apWjq+LSjh49yhNPPMGSJUvw8fFxdHXcht1up1OnTrzxxhsAdOjQge3bt/Ppp58ycuRIB9fONX333XfMmDGDb7/9ltatWxMdHc2TTz5JQECAPlM3oK4uN1SzZk08PT1zzYaJi4ujTp06DqqVaxo3bhwLFixg2bJl1KtXL/v1OnXqkJ6eztmzZ3Ocr884f5s3byY+Pp4bbrgBLy8vvLy8WLFiBZMmTcLLywt/f399pkVQt25dWrVqleO1li1bcuTIEYDsz06/Dwrun//8J88++yz33nsvbdu25YEHHmD8+PG8+eabgD5TKxTkM6xTp06uCTkZGRmcPn26WJ+zgo8b8vb2pmPHjkRFRWW/ZrfbiYqKolu3bg6smeswDINx48Yxd+5cli5dSsOGDXMc79ixI+XKlcvxGe/Zs4cjR47oM85H37592bZtG9HR0dm3Tp06MXz48OzH+kwLr3v37rmWWti7dy/BwcEANGzYkDp16uT4XJOSkli/fr0+13ykpqbi4ZHz69HT0xO73Q7oM7VCQT7Dbt26cfbsWTZv3px9ztKlS7Hb7XTp0qXohRd5WLQ4tZkzZxrly5c3pk+fbuzcudMYM2aMUbVqVePEiROOrppLeOyxxww/Pz9j+fLlxvHjx7Nvqamp2ec8+uijRlBQkLF06VJj06ZNRrdu3Yxu3bo5sNau58pZXYahz7QoNmzYYHh5eRmvv/66sW/fPmPGjBlGxYoVjW+++Sb7nLfeesuoWrWqMX/+fOPPP/80br/9dqNhw4bG+fPnHVhz5zVy5EgjMDDQWLBggXHo0CFjzpw5Rs2aNY2nn346+xx9ptd37tw5Y+vWrcbWrVsNwHj//feNrVu3Gn/99ZdhGAX7DG+55RajQ4cOxvr1641Vq1YZTZs2Ne67775i1UvBx419+OGHRlBQkOHt7W2EhoYa69atc3SVXAaQ523atGnZ55w/f974f//v/xnVqlUzKlasaAwZMsQ4fvy44yrtgq4OPvpMi+ann34y2rRpY5QvX95o0aKF8X//9385jtvtdmPChAmGv7+/Ub58eaNv377Gnj17HFRb55eUlGQ88cQTRlBQkOHj42M0atTI+Ne//mWkpaVln6PP9PqWLVuW5+/RkSNHGoZRsM/w1KlTxn333WdUrlzZ8PX1NUaNGmWcO3euWPWyGcYVS1GKiIiIuDGN8REREZEyQ8FHREREygwFHxERESkzFHxERESkzFDwERERkTJDwUdERETKDAUfERERKTMUfERERKTMUPARERGRMkPBR0RERMoMBR8REREpMxR8REREpMxQ8BEREZEyQ8FHREREygwFHxERESkzFHxERESkzFDwERERkTJDwUdERETKDAUfERERKTMUfERERKTMUPARERGRMkPBR0RERMoMBR8REREpMxR8REREpMxQ8BEREZEyQ8FHREREygwFHxERESkzFHxERESkzFDwERERkTJDwUdERETKDAUfERERKTMUfERERKTMUPARERGRMkPBR0RERMoMBR8REREpMxR8REREpMxQ8BEREZEyQ8FHREREygwFHxERESkzFHxERESkzFDwERERkTJDwUdERETKDAUfERERKTMUfERERKTMUPARERGRMkPBR0RERMoMBR8REREpM7wcXQEx2e12YmNjqVKlCjabzdHVERERcRmGYXDu3DkCAgLw8Lh2m46Cj5OIjY2lfv36jq6GiIiIyzp69Cj16tW75jkKPk6iSpUqgPmP5uvr6+DaiIiIuI6kpCTq16+f/V16LQo+TiKre8vX11fBR0REpAgKMlREg5tFRESkzFDwERERkTJDwUdERETKDAUfERERKTMUfERERKTMUPARERGRMsPS6ezLli0jKiqK1atXc+zYMRISEqhYsSK1atWibdu29O7dmwEDBlCnTh0rixUREREpEJthGEZxLpCSksKkSZP4/PPP+euvv8i6nI+PD9WrV+f8+fMkJiZit9sBKFeuHAMHDmT8+PF07969+D+Bm0hKSsLPz4/ExESt4yMiIlIIhfkOLVZX16effkqTJk3417/+ha+vL6+++ipRUVEkJiaSmprKsWPHOHXqFBcvXmT37t18+eWX3H333SxevJhevXpxxx13cOjQoeJUQURERKTAitXiU65cOe677z6efvpp2rRpU+D3nT9/nhkzZvDmm28ycuRIXnjhhaJWwW2oxUdERKRoCvMdWqzgs3fvXpo1a1bUt5OZmcmRI0do2LBhka/hLhR8REREiqbUurqKE3oAPD09FXpK0Oqj8PkWOHTG0TURERFxDtqk1I19sgl+PwJ+5aFhNUfXRkRExPFKJfjs27eP6Ojo7Nsff/zBsWPHSqPoMi3YD34H/kp0dE1EREScQ6GDz+bNm3nhhRc4cOAAnTp14p133qFu3boApKWl8eeff+YIOdu2bSMlJQUge6p7QbaNl+ILrmreK/iIiIiYChV8Dh48SFhYGL179+b1119n2rRp9O3blw4dOhAdHc2+ffvIzMwEyLGej2EYtG7dmgcffJDWrVsXagaYFF0DP/P+r7MOrYaIiIjTKFTwWbBgASkpKXzzzTf4+fnRt29fqlevzp49e/Dw8KBJkya0adOGNm3a0LZtW9q0aUPjxo0pV64c3bp148knnyyhH0PyEnwp+BxWi4+IiAhQyOATEBCAYRisWbOGiIgI1qxZA5hdV0888QQvv/wylSpVKpGKSuEFXQo+SWlw9gJU9XFsfURERBytUNPZhw4dyqBBgxg4cCCNGzdm3Lhx/Oc//6FWrVr897//pWnTpnzxxRcUcxcMsUiFcuB/KYcePuvQqoiIiDiFQgUfm83GvHnzWLt2LRMnTmTr1q384x//YN++fTz99NOcOXOGRx55hJCQEBYvXlxSdZZCaFDVvNcAZxERkSIuYNi5c2cGDBiAn5/Zl1K5cmXefPNNdu/ezZ133sn27duJiIggIiKC7du3W1phKZys7i61+IiIiBRz5earBQcHM2vWLFatWkWnTp1YtGgRHTp00PR1B8qe2aUWHxEREWuDT5Ybb7yR9evX8/XXX1O3bl0Mw2DmzJm88847ZGRklESRko/stXzOOrIWIiIizqFEgk+W4cOHs3fvXl5++WUAnn32Wdq1a8eSJUtKsli5glp8RERELivR4APmAoYTJkxg7969jBw5kr179xIREVHSxcolQVXN+5OpkJLu0KqIiIg4XLGDz8cff0xMTMx1z6tTpw5Tp05l48aN9OrVq7jFSgH5lYdql9bvUauPiIiUdcUOPuPGjSMoKIjOnTvz+uuvs23btmue36FDB5YuXVrcYqUQgtXdJSIiAlgQfDZu3Mjzzz9Peno6EyZMoH379jRu3JinnnqKFStWYLfbrainFIMGOIuIiJiKHXw6duzIq6++yh9//MHBgwd59913CQoKYtKkSYSHh+Pv78+oUaOYN28eqampVtRZCkktPiIiIiZLBzc3aNCA8ePHs2zZMuLi4pg2bRo9e/Zk9uzZ3HHHHdSsWZOBAwcydepU4uPjrSxariFr9WYtYigiImWdzSiFjbXS0tJYsmQJ8+fPZ8GCBcTFxeHh4UHXrl1ZtWpVSRfvEpKSkvDz8yMxMRFfX19Lr70xFu78HupVgdWjLb20iIiIwxXmO7RQu7MXVfny5RkwYAADBgzAMAzWrl3L/Pnz+fHHH0uj+DIvay2fmHOQlgHlS+VfXURExPmU+Do+V7PZbNx44428/fbb7Nq1q7SLdzqTJ0+mVatWdO7cucTKqFkRKpYDAzh2rsSKERERcXrF6uoaPbpo/SY2m40pU6YUtVi3VJJdXQARM2BnAkwdBH0bWn55ERERhym1rq7p06cX6X0KPqUvuKoZfI5oZpeIiJRhxQo+hw4dsqoeUsKyprRrZpeIiJRlxQo+wcHBVtVDSljWlHat5SMiImVZqQ9uFscIylrE8KxDqyEiIuJQJTKxefXq1UyfPp3o6GiSkpLw9fWlQ4cOjBgxgh49epREkXIdWVPajyZBph08FXlFRKQMsjz4jB8/nkmTJpE1Wcxms2EYBps3b2bKlCk88cQTvP/++1YXK9dRpzJ4e0J6JsQmQ33rJ46JiIg4PUv/7v/yyy+ZOHEiTZs2ZcaMGcTGxpKRkcHx48f59ttvadasGRMnTuSrr76yslgpAE+Py2FH3V0iIlJWWbplRdeuXYmNjWXbtm34+fnlOp6YmEjbtm0JCAhg3bp1VhXrFkp6HR+AUfNh6WF4IxyGty2RIkREREpdYb5DLW3x2bFjB0OHDs0z9AD4+fkxdOhQduzYYWWxUkDarFRERMo6h2xZIY4RXNW8P3TWkbUQERFxHEuDT+vWrfnhhx9ITk7O8/i5c+f44YcfaN26tZXFSgE1q27e7znl2HqIiIg4iqXB55FHHuHYsWN069aNH374gYSEBAASEhKYPXs2N954I8eOHeOxxx6zslgpoOY1zPsjiZB60bF1ERERcQRLp7OPGjWKrVu38tFHH3H33XcD4OHhgd1uB8AwDB5//HFGjhxpZbFSQDUqQq2KcDIV9p6C9nUcXSMREZHSZfk6PpMmTeKuu+7KcwHDkSNH0rNnT6uLlEJoVsMMPnsUfEREpAwqkZWbe/bsqYDjpFrUgNVHNc5HRETKJm1cUMY0uzTOZ0+CY+shIiLiCCXS4pOZmcmxY8eIjY3l4sW8R9H26tWrJIqW62he07xXi4+IiJRFlgYfu93OG2+8wcSJEzl9+vQ1z83MzLSyaCmgrCntJ1Ph9HmoXsGx9RERESlNlgaf5557jnfeeYfatWszatQo6tati5dXiTQqSRFV8jb37DqaZLb6dKvn6BqJiIiUHktTyZdffknz5s3ZuHEjlStXtvLSYqHmNRR8RESkbLJ0cHNycjK33XabQo+Tyx7nowHOIiJSxlgafNq1a0dsbKyVl5QSkLWCswY4i4hIWWNp8PnXv/7FvHnz2LJli5WXFYu1uBR89p4Cw3BsXUREREqTpWN8brvtNqZPn05ERASDBg0iJCQEX1/fPM8dMWKElUVLITSsBl4ecC4dYs9BYN7/RCIiIm7H0uCTlpbGTz/9REJCAlOmTAHAZrPlOMcwDGw2m4KPA3l7QqNqZovPnlMKPiIiUnZYGnwiIyOZMWMG7dq1484779R0difWosbl4BPe0NG1ERERKR2WppLvv/+ejh07snbtWgUeJ9dMA5xFRKQMsnRw84ULFwgLC1PocQHNtWeXiIiUQZYGn44dO7J//34rLyklpMWltXz2n4EMu2PrIiIiUlosDT5vvPEGv/76KwsWLLDyslIC6vlCxXKQngmHzzq6NiIiIqXD0j6pJUuW0KdPH26//XbCw8Pznc5us9mYMGGClUVLIXnYzA1Lo+PMcT5Nqju6RiIiIiXPZhjWLWHn4VGwBiSbzabd2a+SlJSEn58fiYmJ+a59ZLV/LoHvdsIToRDZrVSKFBERsVxhvkMtbfFZtmyZlZeTEpY1wHm3ZnaJiEgZYWnw6d27t5WXkxLWQpuViohIGVPswc0ff/wxMTExVtRFSlnWWj5/JcKFDMfWRUREpDQUO/iMGzeOoKAgOnfuzOuvv862bdusqJeUgloVoZoPGMC+046ujYiISMkrdvDZuHEjzz//POnp6UyYMIH27dvTuHFjnnrqKVasWIHdrkVinJXNdnmczz6N8xERkTKg2MGnY8eOvPrqq/zxxx8cPHiQd999l6CgICZNmkR4eDj+/v6MGjWKefPmkZqaakWdxULaukJERMoSSxcwbNCgAePHj2fZsmXExcUxbdo0evbsyezZs7njjjuoWbMmAwcOZOrUqcTHx1tZtBSRgo+IiJQllq7jk5+0tDSWLFnC/PnzWbBgAXFxcXh4eNC1a1dWrVpV0sW7BEes4wOwIQbumg2BVWDN6FIrVkRExDIOW8cnP+XLl2fAgAEMGDAAwzBYu3Yt8+fP58cffyyN4uUaslp8Ys7BuTSoUt6x9RERESlJlnZ1FYTNZuPGG2/k7bffZteuXaVdvFylqg/4VzIfa2aXiIi4u2K1+IweXbS+EZvNxpQpU4pTtFioeQ2ISzHH+dxQ19G1ERERKTnFCj7Tp08v0vsUfJxL0xqw8gjs1QBnERFxc8UKPocOHbKqHuJAzTWzS0REyohiBZ/g4GCr6iEOlBV81OIjIiLurtQHN4vzaVrdvD+ZCqfPO7YuIiIiJanEprNnZmaSkJBAWlpanseDgoJKqmgppEreUN8XjiaZrT5d6zm6RiIiIiXD8uCzefNmnn/+eVauXEl6enqe59hsNjIytB24M2lewww+exR8RETEjVna1RUdHU3Pnj1Zu3YtN998M4Zh0K5dO26++WZq1qyJYRj07t2bBx54wMpixQLNNM5HRETKAEuDz6uvvgrA+vXrmT9/PgBDhgxh4cKFHD58mEcffZTt27fz4osvWlmsWEDBR0REygJLg8+qVasYNGgQLVu2zH4tayuwChUq8NFHHxEQEMDzzz9vZbFigSuntJf87m0iIiKOYWnwSUxMpFGjRtnPy5UrR3Jy8uXCPDzo06cPUVFRVhYrFmhUDTxtkJgG8SmOro2IiEjJsDT41K5dmzNnzmQ/r1OnDvv27ctxzoULF0hNTbWyWLGAjxc0qGo+1kKGIiLiriwNPq1atWLPnj3Zz7t3787ixYtZu3YtALt27eK7776jRYsWVhYrFtEKziIi4u4sDT633XYbK1eu5Pjx4wA888wzGIZBjx49qFWrFm3btuXs2bMa4+OkNMBZRETcnaXB59FHHyUmJoYaNcxv0JCQEKKiorjllluoWbMm/fr146effmLIkCFWFisWUfARERF3Z+kChuXKlcPf3z/HazfeeCM///yzlcVICcnes+s02A3wsDm2PiIiIlbTXl2SrUFV8PaE1ItwLMnRtREREbGepcFn9erVREZGcuLEiTyPHz9+nMjISNatW2dlsWIRLw9oVNV8vP+0Q6siIiJSIiwNPu+//z4//fQTderUyfN43bp1WbBgAf/973+tLNYpLViwgObNm9O0aVO++OILR1enwBpf2qn94JlrnyciIuKKLA0+GzdupEePHtc8p1evXm7f4pORkUFkZCRLly5l69atvPPOO5w65RojhhtVM+8PKPiIiIgbsjT4xMfHExgYeM1z6tSpQ3x8vJXFOp0NGzbQunVrAgMDqVy5MhERESxevNjR1SqQxgo+IiLixiwNPlWrVuXIkSPXPOevv/6icuXKxS7rrbfewmaz8eSTTxb7WldauXIlAwcOJCAgAJvNxrx58/I8b/LkyTRo0AAfHx+6dOnChg0bso/FxsbmCICBgYHExMRYWs+SkhV81NUlIiLuyNLg07VrV+bOncvRo0fzPH7kyBHmzZvHjTfeWKxyNm7cyGeffUa7du2ued7q1au5ePFirtd37txJXFxcnu9JSUkhJCSEyZMn53vdWbNmERkZyYsvvsiWLVsICQmhf//+btGSldXVdTLV3LdLRETEnVgafCIjI0lNTaV79+589dVX2Ss4Hz9+nC+//JLu3btz/vx5nnrqqSKXkZyczPDhw/n888+pVq1avufZ7XbGjh3LsGHDyMzMzH59z549hIeH8+WXX+b5voiICF577bVrLrL4/vvv8/DDDzNq1ChatWrFp59+SsWKFZk6dSoAAQEBOVp4YmJiCAgIKOyP6hCVvaHOpQY5tfqIiIi7sTT49OrVi/fff5/Y2FhGjRpFvXr18PLyol69eowePZoTJ04wceJEevXqVeQyxo4dy2233Ua/fv2ueZ6Hhwe//PILW7duZcSIEdjtdg4cOEB4eDiDBw/m6aefLlL56enpbN68OUf5Hh4e9OvXL3tPstDQULZv305MTAzJycksXLiQ/v3753m9yZMn06pVKzp37lyk+pSErCntBzSlXURE3IylKzcDPPHEE4SFhfHpp5+yceNGEhMTqVq1KqGhoTz66KO0adOmyNeeOXMmW7ZsYePGjQU6PyAggKVLl9KzZ0+GDRvG2rVr6devH5988kmR65CQkEBmZmauFar9/f3ZvXs3AF5eXrz33nuEhYVht9t5+umns7fxuNrYsWMZO3YsSUlJ+Pn5FbleVmpcHdYc0wBnERFxP5YHH4B27drx8ccf53s8MzMTT0/PQl3z6NGjPPHEEyxZsgQfH58Cvy8oKIivv/6a3r1706hRI6ZMmYLNVvJ7MQwaNIhBgwaVeDklQTO7RETEXVna1XWtAcFZMjMzuffeewt97c2bNxMfH88NN9yAl5cXXl5erFixgkmTJuHl5ZVjHM+V4uLiGDNmDAMHDiQ1NZXx48cXuuwr1axZE09Pz1yDo+Pi4vJduNHVKPiIiIi7sjT4/P3vf2f27Nn5Hrfb7dx7773MmTOn0Nfu27cv27ZtIzo6OvvWqVMnhg8fTnR0dJ4tSAkJCfTt25eWLVsyZ84coqKimDVrFv/4xz8KXX4Wb29vOnbsSFRUVI6fKyoqim7duhX5us4kK/j8dRYy7A6tioiIiKUs7erq0aMHDzzwADVq1CAsLCzHMbvdzn333ccPP/zAuHHjCn3tKlWq5BofVKlSJWrUqJHnuCG73U5ERATBwcHMmjULLy8vWrVqxZIlSwgPDycwMDDP1p/k5GT279+f/fzQoUNER0dTvXp1goKCAHP22siRI+nUqROhoaF88MEHpKSkMGrUqEL/XM6obhXw8YILGXA0ERrmP3lORETEpVgafH766Sd69uzJkCFDWL58Oe3btwfMEDJ8+HC+//57/t//+39MmjTJymLz5OHhwRtvvEHPnj3x9vbOfj0kJITffvuNWrVq5fm+TZs25QhtkZGRAIwcOZLp06cDcM8993Dy5EleeOEFTpw4Qfv27fn1119zDXh2VR42cz2fnSfN7i4FHxERcRc2wzAMKy944sQJunXrxoULF1i9ejUNGzbkvvvu47vvvuPRRx+95qDnsixrVldiYiK+vr6Org7jFsJPe+H5HvBIR0fXRkREJH+F+Q61dIwPmHtxLVq0iMzMTG6++WbuvvtuvvvuOx5++GGFHheiAc4iIuKOLA8+AM2aNeOXX34hPj6eOXPm8NBDD/HZZ5+VRFFSQrKDjxYxFBERN1KsMT6vvPLKNY+HhoYSHR1NQEBAjnNtNhsTJkwoTtFSwrL27Dp41qHVEBERsVSxxvh4eBStwchms+W77k5Z5WxjfFIvQstLPZPRY6BaBcfWR0REJD+F+Q4tVovPsmXLivN2cWIVy0FAZYhNNsf5dFLwERERN1Cs4NO7d2+r6iFOqHH1K4KPa2wuLyIick0lMrhZ3INmdomIiLtR8JF8ZQ9wVvARERE3Uazgc8stt7Bx48YivTclJYW33nqrQBubimNoSruIiLibYgWfkydP0rVrV8LCwpg2bRqJiYnXfc+6desYN24cwcHBvPrqq26zzYM7yt6sNBHSNQlPRETcQLG3rPjyyy95+eWXOXz4MB4eHjRv3pyOHTvi7+9P1apVuXDhAqdPn2bPnj1s2rSJc+fO4enpyb333strr72WvfFnWeds09kBDANafWJObY96AJpUd3SNREREcivMd6gle3UZhsEvv/zCtGnTWL58OadP5+4b8fDwoF27dgwZMoSHHnqIunXrFrdYt+KMwQdgwP9gWzz83wDo39jRtREREcmt1NbxyWKz2bjtttu47bbbANi1axfHjh3j1KlTVKhQgVq1atG6dWv8/PysKE5KUeNqZvDZe0rBR0REXJ8lwedqLVu2pGXLliVxaSllbWrDvD3wZ5yjayIiIlJ8ms4u19T+0tjzrSfMMT8iIiKuTMFHrqlNbfC0wclUiD3n6NqIiIgUj4KPXFOFctCipvk4Wt1dIiLi4hR85Lo61DHvo084th4iIiLFpeAj19VewUdERNyEgo9cV1bw2RYPGXbH1kVERKQ4LA0+np6eDB8+3MpLihNoXA18veF8Buw55ejaiIiIFJ2lwcfX15f69etbeUlxAh42aHdpWru6u0RExJVZGnxCQ0P5448/rLykOIms7q6tCj4iIuLCLA0+L730EkuXLuWrr76y8rLiBDTAWURE3IGlW1YsWbKEPn36MGrUKD788EM6d+6Mv78/Npstx3k2m40JEyZYWbSUsKwVnPefhnNpUKW8Y+sjIiJSFJbszp7Fw6NgDUg2m43MzEyrinULzro7+5W6T4Vj5+DbO6C7hnKJiIiTKPXd2bMsW7bMysuJk2lfxww+0ScUfERExDVZGnx69+5t5eXEybSvAwv2aZyPiIi4Li1gKAV25cwu7dQuIiKuyNIWnyyrV69m+vTpREdHk5SUhK+vLx06dGDEiBH06NGjJIqUUtC2Nnh5XN6pPdA5hyKJiIjky/LgM378eCZNmkTWmGmbzYZhGGzevJkpU6bwxBNP8P7771tdrJQCHy9zp/bt8eZO7Qo+IiLiaizt6vryyy+ZOHEiTZs2ZcaMGcTGxpKRkcHx48f59ttvadasGRMnTtQ6Py6svVZwFhERF2bpdPauXbsSGxvLtm3b8PPzy3U8MTGRtm3bEhAQwLp166wq1i24wnR2gNk74akl0KEOzLvH0bUREREp3HeopS0+O3bsYOjQoXmGHgA/Pz+GDh3Kjh07rCxWSlHWNPboE3DmvGPrIiIiUlilPqvr6lWcxbXUrQItaoABrDzi6NqIiIgUjqXBp3Xr1vzwww8kJyfnefzcuXP88MMPtG7d2spipZT1aWDeLz/syFqIiIgUnqXB55FHHuHYsWN069aNH374gYSEBAASEhKYPXs2N954I8eOHeOxxx6zslgpZVnBZ8VfYNd6PiIi4kIsnc4+atQotm7dykcffcTdd98NmPt32e12AAzD4PHHH2fkyJFWFiulrFNdqOwNp86bU9vb+Tu6RiIiIgVj+To+kyZN4q677spzAcORI0fSs2dPq4uUUlbO0xzkvOgALDus4CMiIq6jRFZu7tmzpwKOmwtrYAaf5X/BE10cXRsREZGCsXSMj6enJ8OHD7fykuKk+gSb99En4OwFx9ZFRESkoCwNPr6+vtSvX9/KS4qTqlsFmtcwBzev/MvRtRERESkYS4NPaGgof/zxh5WXFCeWPa1dwUdERFyEpcHnpZdeYunSpdqLq4zI6u5acVjT2kVExDVYOrh5yZIl9OnTh1GjRvHhhx/SuXNn/P39c63WbLPZmDBhgpVFiwN0CoBK5SDhPOyIh7aa3SUiIk7O0k1KPTwK1oBks9nIzMy0qli34CqblF5tzAJzdldkV83uEhERxyjMd6ilLT7Lli2z8nLiAjStXUREXImlwad3795WXk5cwJXT2k+fh+oVHFsfERGRa9E6PlIsdatAq1rm4OZlhx1dGxERkWvTOj5SbDc1NO+XHHRsPURERK5H6/hIsd3UyLxf8RdcyHBsXURERK5F6/hIsbWpDf6VIPUirD3m6NqIiIjkT+v4SLHZbGarzzfb4LeD5kwvERERZ6R1fJyEq67jk2X5YRg532z5Wf+gGYZERERKg9bxkVLXrZ65inNcCmzXKs4iIuKktI6PWKK8F/QKhoX7YfFBBR8REXFOlg5uLoj09HSSkpJKu1gpBVmzu37TtHYREXFSxQ4+jRo1YtKkSTleW7RoEZGRkXme/+abb1KtWrXiFitOKKwBeNhgZwIcU7YVEREnVOzgc/jwYc6ePZvjtXXr1jFx4sTiXlpcTPUK0Kmu+fi3Q46ti4iISF5KvatL3NtNjc17dXeJiIgzUvARS2VtX7HuGCSlObYuIiIiV1PwEUs1rAaNq8FFOyw+4OjaiIiI5KTgI5Yb3MK8/36XY+shIiJyNQUfsdydLcGG2d11JNHRtREREbnMkgUMv/nmG9atW5f9fP/+/QDceuutuc7NOibuK6AK9AiC34/A7J0Q2c3RNRIRETEVe6+ugu7PlaNQ7dWVi6vv1XW1+Xvg779CvSrw+yhzfR8REZGSUKp7dR06pAVbJLf+jcHXG46dgzVHzRYgERERRyt28AkODraiHuJmfLxgYDOYsR2+36ngIyIizkGDm6XE3NXavF+4X2v6iIiIc1DwkRLT3h+aVIe0TFiw19G1ERERUfCREmSzwV2tzMff7XRsXUREREDBR0rYHS3A0wZbT8C+046ujYiIlHUKPlKialeCPg3MxzO2ObQqIiIiCj5S8kaFmPffboPj5xxbFxERKdsUfErIggULaN68OU2bNuWLL75wdHUcqkcQdAk0Bzl/tNHRtRERkbJMwacEZGRkEBkZydKlS9m6dSvvvPMOp06dcnS1HMZmg6cubVsxc4f27xIREcexZK+uK6WnpzNv3jw2btzI2bNn89yawmazMWXKFKuLdhobNmygdevWBAYGAhAREcHixYu57777HFwzx+kSCL2CYOURmLQe3r3Z0TUSEZGyyNLg89dff3HTTTdx4MABrrUFWFGDzyeffMInn3zC4cOHAWjdujUvvPACERERRa1yLitXruSdd95h8+bNHD9+nLlz5zJ48OBc502ePJl33nmHEydOEBISwocffkhoaCgAsbGx2aEHIDAwkJiYGMvq6Kqe6mYGnx92w2OdoXE1R9dIRETKGku7usaPH8/+/fu5//77WbZsGfv27ePQoUO5bgcPHizS9evVq8dbb73F5s2b2bRpE+Hh4dx+++3s2LEjz/NXr17NxYsXc72+c+dO4uLi8nxPSkoKISEhTJ48Od96zJo1i8jISF588UW2bNlCSEgI/fv3Jz4+vkg/V1nRvg7c1AjsBnywztG1ERGRMsmwkJ+fn9GvXz8rL3ld1apVM7744otcr2dmZhohISHGnXfeaWRkZGS/vnv3bsPf3994++23r3ttwJg7d26u10NDQ42xY8fmKCsgIMB48803DcMwjNWrVxuDBw/OPv7EE08YM2bMuGZZiYmJBmAkJiZet16ubEe8YQR9YN52xju6NiIi4g4K8x1qaYuP3W6nQ4cOVl4yX5mZmcycOZOUlBS6deuW67iHhwe//PILW7duZcSIEdjtdg4cOEB4eDiDBw/m6aefLlK56enpbN68mX79+uUoq1+/fqxduxaA0NBQtm/fTkxMDMnJySxcuJD+/fvneb3JkyfTqlUrOnfuXKT6uJpWtWBAU/Px66sg0+7Y+oiISNliafDp0qULu3btsvKSuWzbto3KlStTvnx5Hn30UebOnUurVq3yPDcgIIClS5eyatUqhg0bRnh4OP369eOTTz4pcvkJCQlkZmbi7++f43V/f39OnDgBgJeXF++99x5hYWG0b9+ep556iho1auR5vbFjx7Jz5042biw787zHd4XynvD7EXhnjaNrIyIiZYmlweett95i6dKlzJ4928rL5tC8eXOio6NZv349jz32GCNHjmTnzvw3ggoKCuLrr79m1qxZeHl5MWXKFGw2W4nVL8ugQYPYu3cv+/fvZ8yYMSVenitpUh3evtRg9slmmLPbsfUREZGyw9JZXT///DNhYWHcc8899O7dmxtuuAFfX99c59lsNiZMmFCkMry9vWnSpAkAHTt2ZOPGjUycOJHPPvssz/Pj4uIYM2YMAwcOZOPGjYwfP54PP/ywSGUD1KxZE09Pz1yDo+Pi4qhTp06Rr1vWDGkB+07B5E3w7G/QsCp00McnIiIlzNLg89JLL2U/Xr58OcuXL8/zvOIEn6vZ7XbS0tLyPJaQkEDfvn1p2bIl33//PXv37qVPnz6UL1+ed999t0jleXt707FjR6KiorKnudvtdqKiohg3blxRf4wy6R83mhuXLj4ID/8EP90Ldas4ulYiIuLOLA0+y5Yts/JyuTz33HNEREQQFBTEuXPn+Pbbb1m+fDmLFi3Kda7dbiciIoLg4ODsbq5WrVqxZMkSwsPDCQwMZPz48bnel5yczP79+7OfHzp0iOjoaKpXr05QUBAAkZGRjBw5kk6dOhEaGsoHH3xASkoKo0aNKrkf3g152OCD/jD0e9iVAA8tgO/vhIrlHF0zERFxVzbDuMZKg07mwQcfJCoqiuPHj+Pn50e7du145plnuOmmm/I8f8mSJfTs2RMfH58cr2/dupVatWpRr169XO9Zvnw5YWFhuV4fOXIk06dPz37+0UcfZS9g2L59eyZNmkSXLl2K/LMlJSXh5+dHYmJint2D7uxYEgyaCafOQ//G8OltZigSEREpiMJ8h7pU8HFnZTn4AGyKhWFzzI1MH+0Iz/VwdI1ERMRVFOY7tEQ2KV29ejUPP/wwnTt3pnnz5nTu3JkxY8awatWqkihO3ECnAPjPpZlen26G/213bH1ERMQ9Wd7iM378eCZNmpS9V5fNZsvx+IknnuD999+3ski3UNZbfLJ8sA7+ux68PODL26FHkKNrJCIizs5hLT5ffvklEydOpGnTpsyYMYPY2FgyMjI4fvw43377Lc2aNWPixIl89dVXVhYrbuSJLnB7c8iww2O/wK6Tjq6RiIi4E0tbfLp27UpsbCzbtm3Dz88v1/HExETatm1LQEAA69Zpl8orqcXnsgsZ5nifzcehqg98MwTa1nZ0rURExFk5rMVnx44dDB06NM/QA+Dn58fQoUPz3U1dBMDHC6bdbi5oePYCDPsBtp5wdK1ERMQdlMjg5mspje0ixPX5lYevB0PnAEhKh+FzYEOMo2slIiKuztLg07p1a3744QeSk5PzPH7u3Dl++OEHWrdubWWx4qaqlIevBsON9SDlIoyYB7//5ehaiYiIK7M0+DzyyCMcO3aMbt268cMPP5CQkACYW0fMnj2bG2+8kWPHjvHYY49ZWay4sYrlzG6v3sFwPgP+9iPMzn9PWhERkWuyfDr73//+dz766KPsLi0PDw/sdjsAhmHw+OOPM3HiRCuLdAsa3HxtaRnwjyXw417zeWRX+HsoqOdUREQcvnLz77//zvTp04mOjiYpKQlfX186dOjAyJEj6dmzp9XFuQUFn+uzG/DOGvh4k/n8rpbwZl8o5+nYeomIiGM5PPhI4Sn4FNyMbfDvZWYQ6lEfPr7NHAwtIiJlk8O3rBApScPbwpSB5vifVUdhyCw4fNbRtRIREVdQrBaf0aNHY7PZeOONN/D392f06NEFK9RmY8qUKUUt1i2pxafwdpyEh36E2GRzocNPb4Nu9RxdKxERKW2l1tXl4eGBzWZj165dNGvWDA+PgjUg2Ww2MjMzi1qsW1LwKZr4FHj4J4iOM/f3ej0M7m3j6FqJiEhpKsx3qFdxCjp06BAAgYGBOZ6LlJbalWDWneaMr5/2wjNRsPc0/KsHeKojV0RErqLBzU5CLT7FYxjwwXrzBhDWAD68xVwEUURE3JvDBjcfOXKEpKSka55z7tw5jhw5YmWxIthsML4rTI6A8p6w7DAM+Q6OJDq6ZiIi4kwsDT4NGza87uKEkyZNomHDhlYWK5JtQDOYfRf4V4J9p2HQTFh3zNG1EhERZ2Fp8DEMg+v1nKlnTUpaO3/48V5oVxvOXIDhc821f0REREp9+OexY8eoUqVKaRcrZUydyvD9XTCoGWTY4fmlMGEZXNRkQhGRMq1Ys7oAXnnllRzPly9fnud5mZmZHD16lJkzZ9K1a9fiFityXT5eMOkWaF4D3lkLX/1pdn99citUq+Do2omIiCMUe1bXlWv32Gy263ZlBQQEMHfuXDp37lycYt2OZnWVrMUH4MlFkHIR6vnC/w2A1rUcXSsREbFCqe7VtWLFCsAcuxMeHs7f/vY3Ro4cmes8T09PqlevTosWLQq80GFZouBT8vYkwEMLzJlePl7wVl8Y0sLRtRIRkeJy2CalL7/8MmFhYfTq1cuqS5YZCj6l4+wF+PuvsOIv8/no9vB8D+3wLiLiyrQ7uwtS8Ck9mXZ4fx18tNF83iXQXOzQv7Jj6yUiIkVTaltWXEtmZiYJCQmkpaXleTwoKKikiha5Jk8P+OeN5rT3yMWwPgZu/RYm3gI99J+liIhbs7zFZ/PmzTz//POsXLmS9PT0vAu12cjIyLCyWJenFh/HOHgG/t8vsCsBbMATXeDvodrnS0TElThsy4ro6Gh69uzJ2rVrufnmmzEMg3bt2nHzzTdTs2ZNDMOgd+/ePPDAA1YWK1JkjarBvHvg3tZgYO719cA8iEtxdM1ERKQkWBp8Xn31VQDWr1/P/PnzARgyZAgLFy7k8OHDPProo2zfvp0XX3zRymJFisXHC97uB/+9GSp4weqjcMsM+O2go2smIiJWszT4rFq1ikGDBtGyZcvs17J60ipUqMBHH31EQEAAzz//vJXFiljijpbw033QqiacPg8P/gT/WgrnLzq6ZiIiYhVLg09iYiKNGjXKfl6uXDmSk5MvF+bhQZ8+fYiKirKyWBHLNK1udn091MF8/s02GDAT5u2GlLyHrImIiAuxdFZX7dq1OXPmTPbzOnXqsG/fvhznXLhwgdTUVCuLFbFUeS+Y0At6B5uzvvafhicWmd1gNzWCwc2hV7DW/hERcUWWtvi0atWKPXv2ZD/v3r07ixcvZu3atQDs2rWL7777jhYttFyuOL9ewbD4fngiFIL94HwG/LgXRv8Et/4P/jjh6BqKiEhhWRp8brvtNlauXMnx48cBeOaZZzAMgx49elCrVi3atm3L2bNnNcZHXEb1ChDZDVaMhB/vMVd6ruYDe0/B4O/grVVwQSsziIi4DEvX8bl48SKnT5+mWrVqeHt7A7BmzRpef/11Dh48SHBwMI8//ji33XabVUW6Da3j4zpOn4eXVsD8S42bjavBuzfBDXUdWy8RkbJKW1a4IAUf17PogDnr62Squfjh8Lbw9I3g5+PomomIlC0OW8BQpCzp3xh+ewCGtjQXP/xmG4R/BXN2g/6cEBFxTsVq8Rk9enTRCrXZmDJlSlGLdUtq8XFta4+ZrT8HLk1q7FYPXu4NzWs6tl4iImVBqXV1eXjk3WBks9nI67JZr9tsNjIzM4tarFtS8HF96Znw+RaYuB7SMsHDZnZ/RXY1B0mLiEjJKLWurkOHDuW4HThwgAEDBlCjRg1effVVli9fzq5du1i+fDmvvPIKNWrUYODAgbnW9hFxB96eMLaz2f0V0QTsBnz9J/T+EqZuhYvK+iIiDmfp4Oa33nqL//73v0RHR1O3bu4pLjExMXTo0IF//OMfPP3001YV6xbU4uN+1h6Dl1eYO7+DOfvrXz0gvCHYbI6tm4iIO3HY4OYpU6Zw99135xl6AAIDA7n77rv5/PPPrSxWxCl1qwc/3wdvhptdXQfOmIsfDp8Lu046unYiImWTpcHn2LFj+Phcey6vj48Px44ds7JYEafl6QHD2poLID7a0ewOW33UXPn52ShI0O4tIiKlytKurqZNm2IYBtu3b88zAKX+//buPKzqMu/j+PscdmUTEBAVxNQUTTMVcNBwIW2ZyqypzMrUapqoXHrGaZppamYqp5qaSnvqmSWraTNt1HTSIvctItPUUNQUd8GVRUCE83v+uBUlcIOjh8P5vK7rd+n5nfv87pv7Us73urdvSQlXXHEFdrtd63x+QlNdnmFHAbywHOac+Ocf7AtjkmBEN+X+EhGpK5dNdd1///1s3bqVlJQUZs2axcGDBwE4ePAgM2fOpE+fPuTm5vLAAw84s1oRtxEbAm9cD9Nvg87NobAc/rwUBn8Ai7e7unUiIo2fU0d8HA4HDzzwAFOmTMF2YvWm3W7H4XAAYFkWI0eO5J///GfV+2JoxMfzVDrgk2x4cYVJgwEmI/zv+0KHcNe2TUTEnbg8ZcXixYt59913Wbt2LQUFBYSEhNCtWzfuuece+vXr5+zqGgUFPp6r4Bi89jW8uxYqHOb8n2GdYVwyNG/q6taJiDR8Lg985MIp8JFth2HicpMDDKCpD9zfHe6/CoL9XNs2EZGGTLm6RNxQfDP4+8/hk9ugayQcPQ6vfQN9psAbWXC03NUtFBFxfxrxaSA04iOnc1gwbwu88jVsPmTuhQdAn1iID4U2oebPhOZmi7yIiCe7kO9Q7/pUNGrUKGw2G88//zxRUVHnnbRUSUpFzs5ug+vbmwzwn22CV7+G3AKYlVO9XNtQ+OhWiA50STNFRNxOvZOU2mw2NmzYQIcOHc6YtLRGpUpSWoNGfORsKhywONeM/mw7ArlHIPsAFB4zqTCm3qqF0CLiuS7ZiM+2bdsAk4ri9Nci4lzedhjY1lwn7SqEX0wzqTDungEf3wrNlAVeROSstMangdCIj9RF7hH4xXTIPwpdIuHDoRCiHWAi4mEu2YiPiLhWm1AT7NwxHdbnw9BPoEcLsxA6PMCs/enfBpr6urqlIiINQ70XN9eFFjeLOE/7MHj/FrjzU9hyyFynC/WHUVeafGChZ88hLCLS6NV7cXOdKtXi5ho01SX1tbcIFubCwdITVwmsyTOJUcEciHh3Vxh9JURpF5iINCKX7OTm7dvrnlUxLi6uzp9tjBT4yMVQ6YDPt5gDEDccMPe87XB9OxjVHbpHu7Z9IiLOoJQVbkiBj1xMlgULcuGtb+GbPafuXxkFd3aBfnHQIshlzRMRqRctbhaRamw2GBhvrnX58O4amLXJTIWtyTNl2ofB1XHQPw5+1hq8lNBGRBqhizbiU1lZyYEDBzh27Fit78fGxl6Mat2WRnzkUjtQAlN/gIyt8H2eSZNxUotA+EUC3N4ZWuufo4g0cC6d6lq1ahVPPvkkS5Ysoby89qyKNpuNiooKZ1br9hT4iCsdKYPlO2HJdpMd/nCZuW/D5Ad7so/JCyYi0hC5LDv7mjVr6Nu3LytXrmTQoEFYlkXXrl0ZNGgQERERWJZFamoq99xzjzOrFZF6CvWHG9rDC2mQORomXwd9WoMFLN0Bt04zI0MiIu7OqYHPn//8ZwAyMzOZNWsWALfccgtz584lNzeXhx56iPXr1/P00087s1oRcSI/b7ixA3wwFJbeBymtoeQ4PDAb/v6dWSgtIuKunBr4LFu2jJtuuolOnTpV3Ts5kxYQEMDkyZOJiYnhySefdGa1InKRxIbAuzfD8C5m9Oe5pfDEfCjXMVwi4qacGvgUFBTQtu2pLIo+Pj4UFxefqsxup1+/fsyfP9+Z1YrIReTjBc8NgKevBrsNPv4BBrwHzy6Fb/dUXxQtItLQOXU7e2RkJIcPH656HR0dzebNm6uVKSsro6SkxJnVishFZrOZAw/jQmHsPNhZCP/4zlzNm8C17eD2BLgi0pQVEWmonDrik5CQQE5OTtXrlJQUvvzyS1auXAnAhg0b+OSTT+jYsaMzqxWRS2RgPGTeD29eD0MuhyBf2F8C/14LN34M134A/1pt0mWIiDRETt3OPmnSJMaNG8fOnTtp0aIF33//PcnJyZSXlxMWFsbhw4dxOBx8+umn3HLLLc6qtlHQdnZxR+WVsGIn/GcjzNsCx06s/fGxwzVtYVgXsx3erlEgEbmIXHaOz/Hjxzl06BDNmjXD19cXgBUrVvDcc8+xdetW4uLiePTRR7nhhhucVWWjocBH3F1BGXy2CT75Adbmn7rfKhju6Ay/6KS0GCJycVzSwOfYsWP4+fnV5xGCAh9pXLL3w0frYeZGKDxxjqndBn1jzYnQ17QFfyXMEREnuaSBT1hYGHfddRejRo3iqquuqs+jPJoCH2mMyirg881mJ1jm7lP3Q/wguZUZDWoVBC2D4fJwaBPqsqaKiBu7pIFPkyZNKCsrw2az0a1bN0aPHs3w4cMJDQ2tz2M9jgIfaexyj8C0bPh0A+wtrr1MjxZmXdDP20OAzyVtnoi4sUsa+BQVFfHhhx/y9ttvk5WVhc1mw8/PjyFDhjB69GgGDhxYn8d7DAU+4ikqHWb0J+cg7C6CXYXmyt4PlSd+GwX5ws2Xw52doYu2yIvIObhscXN2djZvv/02H3zwAXl5edhsNmJjYxk1ahT33XcfrVu3dlZVjY4CH/F0ecUwfYOZFttRcOp+pwhzRtCQjhAW4Lr2iUjD5dLs7ACVlZXMnj2bt99+m3nz5lFRUYHdbueaa65h9OjR3Hzzzfj4aBz7dAp8RAyHZbbIT/3BZIo/fYt8WluzODo1DrydegqZiLgzlwc+p8vLy+O9995jypQpbNy4EZvNRnh4OPn5+ef+sAdR4CNSU0EZzMqBqdmw/rRfGc2bwNBOcFsn6BDuuvaJSMPQoAKfk9atW8fDDz/M8uXLsdlsVFYqy+HpFPiInF32fpieDTNy4FDpqftdI+G2BLipAzTTVJiIR2owgc/Jhc//+te/WLVqFZZl0bRpU26//Xb+9a9/Xaxq3ZICH5HzU14JC7aZHWKLtkOFw9z3sZuUGredmArz9XJtO0Xk0nF54LNw4ULefvttZsyYQWlpKZZlkZyczOjRo7njjjsIDAx0dpVuT4GPyIU7UGKmwqZvMCNCJ4UFmBGgWzspcaqIJ3BJ4LNr1y6mTJnCO++8Q25uLpZl0bx5c+655x5Gjx5Np06dnFFNo6XAR6R+svebnGEzN5rEqSe1C4OhHeGWjhCjlBkijdIlDXymTp3K22+/zYIFC6isrMRutzNo0KCq3Vve3jqX/nwo8BFxjgoHLN0B/9lQfVeYDXNa9NCOcF07CFKmHZFG45IGPna72VMaHx/PyJEjue+++2jVqlV9HumRFPiIOF/hMZi7xQRBX5+WMsPfGwa1NaNAV2trvIjbu6SBz/Dhwxk9ejQDBgyoz2M8ngIfkYtrVyHM2GiuHw+fuh8RADddbkaCdEq0iHty+eJmuXAKfEQuDcuCtXlmPdBnm6pvjW8XBrdcbk6JbqX/hiJuQ4GPG1LgI3LpHa+EJdvN2UBfnrYeCCCppZkKu74dhPi7ro0icm4KfNyQAh8R1yo6sR5oxkZYuQtO/mL0tkMTH/Onlw287GaL/H3dIKW1psZEGgIFPm5IgY9Iw7GnCD7LMdNhOQfPXK59GIy80owMNVH6QRGXUeDjhhT4iDRMe4qg5LhJnlrpgKPHzdqg6dnm7wDBvmZd0J1doHNz17ZXxBMp8HFDCnxE3EvhMRP8vPM9bC84db9rpAmAbuwAwTorSOSSUODjhhT4iLgnhwUrdsJH682BicdP5A7z94Yb2sPtCWahtNYCiVw8CnzckAIfEfd3sMSsC/r4B9hy6NT9uBCTPPXWjtBS/71FnO5CvkOdfl5pRUUFf/vb30hMTCQ4OLhayoo1a9bw8MMPs2nTJmdXKyLicuFN4IGr4Ku7YeYdMKwLBPqaqbCXV0LKFLjrPyY4Kjnu6taKeCanjviUlpYyaNAgVqxYQUREBD4+Puzdu5fKSnM4RkFBAdHR0Tz++OM8++yzzqq2UdCIj0jjVHLcbJOfng0rdp2639QHrm9vMsgntQS7psJE6sxlIz7PP/88y5cvZ+LEiezbt4/777+/2vshISGkpqbyxRdfOLNaEZEGq4mPCW4+uhWWjYTxyRAbYnaETcuGOz+FPlPgxRWw+dC5nyci9ePUwGfq1Kn079+fCRMmYLPZsNWymq9t27bs2LHDmdWKiLiF1sEwJgmWjIDpt5mpsGBf2F0Eb2RB2r/hho/gn99B3lFXt1akcfI+d5Hzt2PHDm655ZazlgkKCqKgoOCsZUREGjObDXq1NNczqfDVVnNi9KLtsD7fXM8tg5+1MglUr20HIdoaL+IUTg18goKCyM/PP2uZH3/8kebNdcKXiAiYbe8/72CuQ6UwZ5PJHfbdXli201y/Xwj925izgQbG65RokfpwauCTnJzM7NmzOXLkCKGhoTXe37lzJ59//vk5R4VERDxRWADc281c24+YE6Jn5Zi1P1/8aK4AbxP8/LyDCYb8nfpbXKTxc+oan1//+tccPnyYgQMHsnz5cioqKgAoKSlh/vz5DB48mIqKCsaPH+/MakVEGp24UHg0ETLuhnl3wcM9zRqh0gqYsxke+i9c9Xd4dC7M2wJlFTWfoVPaRGpy+gGGb775JmPGjKnawn46Ly8v/vd//7fGbi/RdnYROTfLgrV5MHsz/HcT7Ck+9V4TH+jRAorLzZTZoVKzcywxxkyRXd/ejCiJNEYuP7l5w4YNvPXWW2RmZnLo0CGCg4NJSkri4YcfpnPnzs6urlFQ4CMiF8JhwZp98N/N5pyg3UVnL+9lgz6xcPPlMKgtBGmxtDQiLg985MIp8BGRurIs+D4PNh6AUH8ID4CwJmYtw5dbzVqh9aftO/HzgmvamiAoNQ78tE5I3JzLAp/ly5fz6aefMmHCBKKjo2u8v3fvXl566SVuv/12kpOTnVVto6DAR0Qupq2HYfaJxdI/Hj51P9gPBrc1i6VTWoOPl+vaKFJXLgt8br31VtauXcvmzZvPWKZDhw50796dqVOnOqvaRkGBj4hcCpYF6/ebAOiznOoHJTbzN2cG3dAOklspCBL3cSHfoU4d4MzKymLgwIFnLXP11VeTkZHhzGpFROQ82WxwRaS5fpsCWXvMLrG5m+FAKXy03lyh/mYt0PXtzUiQr4IgaSScGvjk5+fTsmXLs5aJjo4+5yGHIiJy8XnZzchOcitzgvTXu8xi6S9+hIOl8Em2uYJ8YUA8DL4M+sVBU19Xt1yk7pwa+ISGhp4zD9f27dsJDAx0ZrUiIlJP3naz66tPLDzbH77ZA5+f2DG2v8RMjc3KMQuj+8aaxdFpbSGiiatbLnJhnLrGZ8iQIcyfP5/s7Gxat25d4/0dO3bQuXNnBgwYwKxZs5xVbaOgNT4i0hA5LFi9zxyS+MWPsP20VIs24KoWZkpsYFto18xMpYlcai5b3LxkyRL69+9Py5YtefbZZ7nmmmto0aIFe/fu5csvv+T3v/89e/fuZcGCBVx99dXOqrZRUOAjIg2dZUHOQRMAZWyFdT9ZtRAXAmnxZlossaXWBcml49JzfF577TUef/xxTj7WZrNV/d1ut/Pqq6+Snp7uzCobpDlz5vD444/jcDj4zW9+c87TqhX4iIi72VtkAqCvtsHKXVB+2oH9gb7Qp7UJgvq1gaimLmumeACXH2C4du1a3nrrLbKysigoKCA0NJTExEQeeughunTp4uzqGpyKigoSEhJYuHAhISEh9OjRgxUrVhAeHn7GzyjwERF3VlwOS3fA/K2wINcsjj5d5+YmAOoXB92jtVVenMvlgY+nW7FiBS+99BIzZswAYOzYsSQlJTFs2LAzfkaBj4g0Fg4L1uWZAGhhrjlV+nTBvtAh3GSWP3k1CzC5xpJaQkyQK1ot7uxCvkOdmp3dy8uL4cOHO/OR1UycOJFevXoRFBREZGQkQ4YMIScnx6l1LFmyhBtvvJGYmBhsNhszZ86stdwbb7xBmzZt8Pf3JykpiW+++abqvT179lTb1t+yZUt2797t1HaKiDRUdht0i4ZxyfDZnfDt/fC3QSZFRjN/KCyHb/fCsp1mmmzOZvj3Whj7BfR+G1KmwPgv4T8bqh+wKOIMTt3OHhwcXOtuLmdZvHgx6enp9OrVi4qKCp588kkGDRpEdnY2TZvWnEBevnw5iYmJ+Pj4VLufnZ1NeHg4UVFRNT5z9OhRunXrxqhRoxg6dGit7Zg6dSrjx4/nrbfeIikpiVdffZXBgweTk5NDZGSkc35YEZFGonlTGNrJXJUOkzdsdxGUVcKxCiirMK+/2W3e21Vork83mM93DDfb7K+OM9nmA3zOXp/I2Th1qmvw4MHY7Xbmzp3rrEee1f79+4mMjGTx4sU1dok5HA6uuuoq2rdvz8cff4yXl5lQzsnJITU1lfHjxzNhwoSzPt9mszFjxgyGDBlS7X5SUhK9evVi8uTJVXW1bt2aRx99lCeeeKLWqa7ExETuuuuuM9alqS4REbNW6Lu95jDFpTvMzrHTv6T8vKBXDPSNM+cJdYowI0zi2Vw21fXMM8+wYMEC3nvvPWc+9owKCsyBEmFhYTXes9vtfP7556xevZp7770Xh8PBjz/+yIABAxgyZMg5g54zKS8vZ9WqVaSlpVWrKy0tjZUrVwKQmJjI+vXr2b17N8XFxcydO5fBgwfX+rw33niDhIQEevXqVaf2iIg0JoG+ZmRnQgrMHgbfPQiTr4PbEyAmEI5Vmimyicvg+g+hxz/gkbkmzcbOQle3XtyBU6e6MjIy6NevHyNHjmTSpEn06tWLqKgobD850cpms/HUU0/Vqy6Hw8HYsWNJSUk5406xmJgYFixYQN++fbnrrrtYuXIlaWlpvPnmm3Wu98CBA1RWVtaYJouKimLjxo0AeHt78/LLL9O/f38cDgcTJkw4446u9PR00tPTq6JVERE5JSwAbuxgLssymeWX7oAl2+Hr3XCo1GSdn73JlG8dDD9rDT9rBb1baxu91OTUqS67/fwGkGw2G5WVlecueBa/+tWvmDt3LsuWLaNVq1ZnLbtkyRJSU1Np27YtOTk5eHufX7xX21TXyYXLK1asoHfv3lX3J0yYwOLFi8nMzKzTz6OpLhGRC1NeCd/vMyNAy3aYE6Yrf/KNdlkzs1MsuRUkt4QoZUxqlFyWnX3hwoXOfNwZPfLII8yZM4clS5acM+jJy8vjwQcf5MYbbyQrK4tx48YxadKkOtcdERGBl5cXeXnV92fm5eURHR1d5+eKiMiF8fWCXi3NNS7ZrA/K2gMrdsKKXfBDvhkh+vEwfLjefKZNiDlVOqml+bN1sNJseBqnBj6pqanOfFwNlmXx6KOPMmPGDBYtWkR8fPxZyx84cICBAwfSqVMnpk2bxqZNm+jXrx9+fn789a9/rVMbfH196dGjB/Pnz68aCXI4HMyfP59HHnmkTs8UEZH6C/SF/m3MBVBQZpKtfr3LTItl74fcAnN9km3KRAeaxdI9Y8yOscvDTdZ6abycGvhcbOnp6Xz44YfMmjWLoKAg9u3bB0BISAgBAQHVyjocDq677jri4uKYOnUq3t7eJCQkkJGRwYABA2jZsiXjxo2rUUdxcTFbtmyper1t2zbWrFlDWFgYsbGxAIwfP54RI0bQs2dPEhMTefXVVzl69CgjR468iD+9iIhciBB/k0X+mrbmdcExWLXHbJvP3GMOWdxXXH2NUJCvSbza48TVPRqa+rruZxDnuygnNy9fvpx33nmHNWvWUFhYSHBwMN27d+fee++lT58+dX7uTxdJnzRlyhTuu+++GvczMjLo27cv/v7+1e6vXr2a5s2b1zpNtmjRIvr371/j/ogRI3jnnXeqXk+ePJmXXnqJffv2ceWVV/L666+TlJR0YT/QabTGR0Tk0io9DmvyTCD07R5YtReOHq9exm6DED8zmnTyahEIHSPMVvqE5mYBtabLXMulKSvGjRvH66+/XmuSUpvNxpgxY3jllVecWWWjoMBHRMS1Khyw4YAJgFbtMcHQnuJzfy78RLqNnjFm2qxLpDLTX2ouC3zeffddRo4cSYcOHXj66afp378/UVFR5Ofns3DhQv74xz+yadMmpkyZwr333uusahsFBT4iIg1P/lE4UmYWTh8tN+k2dhSY9UIbDsDWwzV3kvl5wZXRJghKbAlXRUOQn2va7ylcFvgkJyezZ88e1q1bV+uZNAUFBVxxxRXExMTw9ddfO6vaRkGBj4iI+ymrMGk2vj0xSpS1Bw6XVS9jt0H7MLgi0owGXRFppsiaKPWG07hsO/sPP/zA/ffff8aD+EJCQrj11lv55z//6cxqRUREXMLf20xx9YwBepw6ZDFrz6lrRwHkHDTX9BP5x2xA22ZmndDJtUJdIiFSBy5edJd8V9eZFiiLiIi4O5sN2oWZa9iJpAJ5xbA23+wiW5dvrv0lp84YmrP51OejmpoRodNHhyK1eNqpLspUV3Z2NoGBNY/HLCoqokuXLrRo0UJTXT+hqS4REc+Rf9SsEdqwH344cW09XD0h60nNm5ggKCHC7CbrGAHxoeCjBdRVXDbV9ctf/pLRo0fTu3dvnnnmGVJTU4mIiODAgQMsWrSIP/7xj+zatYs//elPzqxWRETErUQ2NVdq3Kl7R8vNoun1+82o0Pp82HzIjA4tzDXXSb5e0DYUOoSb0aUO4dAyCA6WmrOJ8orhQCnEhZiziLpEmmk5uQjb2R977DEmT55cNaVlt9txOBzAqZOXX3vtNWdW2ShoxEdERH6q9LgZGVqXDxsPwMaDsOmg2WV2IXzsZh1R+zAzghTRBJo3PfHniSvU332n1Fx6jg/A0qVLaz3AcMSIEfTt29fZ1TUKCnxEROR8WBbsKjIB0OaDZlRo00HYdxQiAkwi1uhAaOYPWw7Bd3vN6M+5eNshLACC/SDQxxzW2NQXmvqYHWgnr2MVkHf01FVcbg55bOZvgqcQf9PGSsucjeSwTG60OztfvOk5lwc+cuEU+IiIyMVgWbCz0GSv31UIB0rM9Nn+Eth/1LwuOHbx23FZM3jq6lO51Jzpkq7xKSwsxN/fH19fJTMRERFpaGw2iA0x15mUV8LBEjMyVFx+6io6BiUVZsrt6HHzp48XRDeFyECzCy3I1ySEPXziKjxmzi7yspsptuJyeOd7s4PtvllmXdPv+5p1Sa5Q7xEfLy8vnnnmGZ566qmqe5mZmWRmZvLYY4/Vu4GeQiM+IiLSWBUeg0nfwJQ1cNwBXjZ4bwj0iXXS8y/gO9Re38osy+KnsdO8efNqzXwuIiIinifYD37XF766Bwa1hdbBJp2HK2hzm4iIiFwSbULhHzeaqTFXJXKt94iPiIiIyIUI8Xdd3Qp8RERExGMo8BERERGP4ZQ1Pu+//3613FtbtmwB4Prrr6+1vM1m47///a8zqhYRERE5b/Xezm63X/igkc1mo7Kysj7VNjrazi4iIlI3l/QAw23bttX3ESIiIiKXRL0Dn7i4uHMXEhEREWkAtLhZREREPIYCHxEREfEYCnxERETEYyjwEREREY+hwEdEREQ8hgIfERER8RjKzt5AnDxHsrCw0MUtERERcS8nvzvP50xmBT4NRFFREQCtW7d2cUtERETcU1FRESEhIWctU++UFeIcDoeDPXv2EBQUhM1mc8ozCwsLad26NTt37lQaDCdSvzqf+vTiUL86n/rU+ZzRp5ZlUVRURExMzDlTaWnEp4Gw2+20atXqojw7ODhY/0EvAvWr86lPLw71q/OpT52vvn16rpGek7S4WURERDyGAh8RERHxGAp8GjE/Pz+efvpp/Pz8XN2URkX96nzq04tD/ep86lPnu9R9qsXNIiIi4jE04iMiIiIeQ4GPiIiIeAwFPiIiIuIxFPiIiIiIx1Dg04i98cYbtGnTBn9/f5KSkvjmm29c3SS3MXHiRHr16kVQUBCRkZEMGTKEnJycamXKyspIT08nPDycwMBAbr31VvLy8lzUYvfzl7/8BZvNxtixY6vuqU/rZvfu3dx9992Eh4cTEBDAFVdcwbffflv1vmVZ/OEPf6BFixYEBASQlpbG5s2bXdjihq2yspKnnnqK+Ph4AgICuOyyy/jzn/9cLQ+U+vTclixZwo033khMTAw2m42ZM2dWe/98+vDQoUMMHz6c4OBgQkNDGT16NMXFxfVqlwKfRmrq1KmMHz+ep59+mu+++45u3boxePBg8vPzXd00t7B48WLS09P5+uuvycjI4Pjx4wwaNIijR49WlRk3bhyzZ89m2rRpLF68mD179jB06FAXttp9ZGVl8X//93907dq12n316YU7fPgwKSkp+Pj4MHfuXLKzs3n55Zdp1qxZVZkXX3yR119/nbfeeovMzEyaNm3K4MGDKSsrc2HLG64XXniBN998k8mTJ7NhwwZeeOEFXnzxRSZNmlRVRn16bkePHqVbt2688cYbtb5/Pn04fPhwfvjhBzIyMpgzZw5LlizhwQcfrF/DLGmUEhMTrfT09KrXlZWVVkxMjDVx4kQXtsp95efnW4C1ePFiy7Is68iRI5aPj481bdq0qjIbNmywAGvlypWuaqZbKCoqstq3b29lZGRYqamp1pgxYyzLUp/W1W9+8xurT58+Z3zf4XBY0dHR1ksvvVR178iRI5afn5/10UcfXYomup0bbrjBGjVqVLV7Q4cOtYYPH25Zlvq0LgBrxowZVa/Ppw+zs7MtwMrKyqoqM3fuXMtms1m7d++uc1s04tMIlZeXs2rVKtLS0qru2e120tLSWLlypQtb5r4KCgoACAsLA2DVqlUcP368Wh937NiR2NhY9fE5pKenc8MNN1TrO1Cf1tVnn31Gz549+cUvfkFkZCTdu3fnH//4R9X727ZtY9++fdX6NSQkhKSkJPXrGfzsZz9j/vz5bNq0CYDvv/+eZcuWcd111wHqU2c4nz5cuXIloaGh9OzZs6pMWloadrudzMzMOtetJKWN0IEDB6isrCQqKqra/aioKDZu3OiiVrkvh8PB2LFjSUlJoUuXLgDs27cPX19fQkNDq5WNiopi3759Lmile/j444/57rvvyMrKqvGe+rRutm7dyptvvsn48eN58sknycrK4rHHHsPX15cRI0ZU9V1tvw/Ur7V74oknKCwspGPHjnh5eVFZWclzzz3H8OHDAdSnTnA+fbhv3z4iIyOrve/t7U1YWFi9+lmBj8g5pKens379epYtW+bqpri1nTt3MmbMGDIyMvD393d1cxoNh8NBz549ef755wHo3r0769ev56233mLEiBEubp17+uSTT/jggw/48MMP6dy5M2vWrGHs2LHExMSoTxsBTXU1QhEREXh5edXYDZOXl0d0dLSLWuWeHnnkEebMmcPChQtp1apV1f3o6GjKy8s5cuRItfLq4zNbtWoV+fn5XHXVVXh7e+Pt7c3ixYt5/fXX8fb2JioqSn1aBy1atCAhIaHavU6dOrFjxw6Aqr7T74Pz9+tf/5onnniCO++8kyuuuIJ77rmHcePGMXHiREB96gzn04fR0dE1NuRUVFRw6NChevWzAp9GyNfXlx49ejB//vyqew6Hg/nz59O7d28Xtsx9WJbFI488wowZM1iwYAHx8fHV3u/Rowc+Pj7V+jgnJ4cdO3aoj89g4MCBrFu3jjVr1lRdPXv2ZPjw4VV/V59euJSUlBpHLWzatIm4uDgA4uPjiY6OrtavhYWFZGZmql/PoKSkBLu9+tejl5cXDocDUJ86w/n0Ye/evTly5AirVq2qKrNgwQIcDgdJSUl1r7zOy6KlQfv4448tPz8/65133rGys7OtBx980AoNDbX27dvn6qa5hV/96ldWSEiItWjRImvv3r1VV0lJSVWZhx56yIqNjbUWLFhgffvtt1bv3r2t3r17u7DV7uf0XV2WpT6ti2+++cby9va2nnvuOWvz5s3WBx98YDVp0sR6//33q8r85S9/sUJDQ61Zs2ZZa9eutW6++WYrPj7eKi0tdWHLG64RI0ZYLVu2tObMmWNt27bN+s9//mNFRERYEyZMqCqjPj23oqIia/Xq1dbq1astwHrllVes1atXW9u3b7cs6/z68Nprr7W6d+9uZWZmWsuWLbPat29vDRs2rF7tUuDTiE2aNMmKjY21fH19rcTEROvrr792dZPcBlDrNWXKlKoypaWl1sMPP2w1a9bMatKkiXXLLbdYe/fudV2j3dBPAx/1ad3Mnj3b6tKli+Xn52d17NjR+vvf/17tfYfDYT311FNWVFSU5efnZw0cONDKyclxUWsbvsLCQmvMmDFWbGys5e/vb7Vt29b63e9+Zx07dqyqjPr03BYuXFjr79ERI0ZYlnV+fXjw4EFr2LBhVmBgoBUcHGyNHDnSKioqqle7bJZ12lGUIiIiIo2Y1viIiIiIx1DgIyIiIh5DgY+IiIh4DAU+IiIi4jEU+IiIiIjHUOAjIiIiHkOBj4iIiHgMBT4iIhdZmzZtaNOmjaubISIo8BERN5Gbm4vNZjvrpeBCRM7F29UNEBG5EJdddhl33313re+FhoZe2saIiNtR4CMibqVdu3Y888wzrm6GiLgpTXWJSKNks9no168fu3btYtiwYURERNCkSRNSUlL46quvav3MgQMHGDt2LPHx8fj5+REZGcntt9/O+vXray1fXl7O3/72N3r16kVQUBCBgYEkJCQwfvx4Dh8+XKN8cXExY8aMISYmBj8/P7p27cr06dNrlCsoKOAPf/gDCQkJBAYGEhwcTLt27RgxYgTbt2+vX8eIeDglKRURt5Cbm0t8fDyDBw9m3rx55yxvs9no2rUrR44coXnz5qSlpbF//36mTp1KWVkZ06dPZ8iQIVXl9+/fT+/evfnxxx/p168fycnJbNu2jenTp+Pn58cXX3xBnz59qsqXlpZyzTXXsHz5ctq3b8+1116Ln58fmzdvJiMjg+XLl3PllVcCZnHz8ePHiYuL4/Dhw6SlpVFSUsLHH39MaWkp8+bNY9CgQQBYlkXv3r3JzMwkJSWFxMRE7HY727dv56uvvmLatGmkpaU5tW9FPIkCHxFxCycDn7Ot8UlOTubaa68FTOADcNddd/H+++9XvV67di29evUiJCSE7du3ExAQAMCoUaOYMmUKv/3tb3n++eernvn5559zww030K5dO3JycrDbzUD5//zP//Dyyy9zzz33MGXKFLy8vKo+U1BQgJeXF4GBgYAJfLZv387NN9/MJ598gq+vLwDz588nLS2tWjC3bt06unbtypAhQ5gxY0a1n+/YsWMcP3686rkiUgeWiIgb2LZtmwWc9RozZkxVecDy8vKycnNzazxr9OjRFmBNnz7dsizLOnbsmOXv72+Fh4dbR48erVH+mmuusQBryZIllmVZ1vHjx62goCArJCTEOnTo0DnbHhcXZwHW1q1ba30vLCys6vXatWstwBo2bNg5nysiF05rfETErQwePBjLsmq9Xn311WplY2NjiYuLq/GMvn37ArB69WoANm7cSFlZGYmJiTRp0qRG+f79+wOwZs2aqvJFRUX06tWLZs2anVe7Q0NDiY+Pr3G/VatWHDlypOp1p06d6Nq1Kx999BFXX301r7zyCt999x0Oh+O86hGRs1PgIyKNVlRU1FnvFxQUAFBYWHjW8i1atKhW7uTnWrZsed5tCQkJqfW+t7d3taDG29ubBQsW8Mgjj7BlyxYef/xxevToQXR0NH/605+orKw87zpFpCYFPiLSaOXl5Z31/slgJDg4+Kzl9+3bV63cyfOCdu/e7bS2ni48PJxJkyaxe/dusrOzmTx5MmFhYTz99NO8+OKLF6VOEU+hwEdEGq0dO3bUuv176dKlAHTv3h2Ajh074u/vT1ZWFiUlJTXKL1q0CKBql9bll19OcHAwWVlZtW5bdxabzUanTp1IT08nIyMDgM8+++yi1SfiCRT4iEijVVlZyZNPPol12ubVtWvX8u9//5vmzZtz/fXXA+Dr68uwYcM4cOAAEydOrPaMefPm8cUXX9CuXTtSUlIAMx31y1/+koKCAsaMGVNj+qmgoIDi4uI6tTk3N5fc3Nwa90+ORvn7+9fpuSJiaDu7iLiF89nODvDEE0/g7+9/1nN8SktL+fTTT2uc45OcnMzWrVsZMGAASUlJ5ObmMm3aNHx9fWuc41NWVsagQYNYunQp7du357rrrsPPz4+tW7cyb948li1bVu0cn5M/w0/169ePxYsXVwVnM2fOZOjQoSQmJpKQkEB0dDS7d+9m5syZFBcXM2PGDG666aZ696eIx3LVdjIRkQtxPtvZAevw4cOWZZnt7KmpqdbOnTutO+64wwoLC7P8/f2t3r17W19++WWtdezfv9967LHHrLi4OMvHx8eKiIiwbrvtNmvdunW1li8rK7P++te/WldeeaUVEBBgBQYGWgkJCdbjjz9e1Q7LMlvW4+Lian1Gamqqdfqv4p07d1pPPPGElZycbEVGRlq+vr5WbGysNXToUGvlypV16jsROUUjPiLSKNlsNlJTU6vW54iIgNb4iIiIiAdR4CMiIiIeQ4GPiIiIeAxvVzdARORi0PJFEamNRnxERETEYyjwEREREY+hwEdEREQ8hgIfERER8RgKfERERMRjKPARERERj6HAR0RERDyGAh8RERHxGAp8RERExGP8P0e3+SZkdZhjAAAAAElFTkSuQmCC\n"
},
"metadata": {}
}
],
"source": [
"import pandas as pd\n",
"\n",
"data = pd.read_csv(f'logs_csv/lightning_logs/version_{csv_logger.version}/metrics.csv')\n",
"fig, ax = plt.subplots(2, figsize=(6,10))\n",
"x = data['epoch'][~data['l2_e_tst'].isnull()]\n",
"y = data['l2_e_tst'][~data['l2_e_tst'].isnull()]\n",
"y2 = data['l2_f_tst'][~data['l2_f_tst'].isnull()]\n",
"ax[0].semilogy(x, y,color='dodgerblue')\n",
"ax[0].set_ylabel('Energy Validation Error (kcal/mol)',size=14)\n",
"ax[1].semilogy(x, y2, label='Force Validation Error (kcal/mol',color='dodgerblue')\n",
"ax[1].set_xlabel('Epochs',size=14)\n",
"ax[1].set_ylabel(r'Force Validation Error (kcal/mol/$\\AA$)',size=14)\n",
"fig.savefig('loss.png', dpi=300)"
]
},
{
"cell_type": "markdown",
"source": [
"### Plotting Training and Validation Loss for $\\Delta$MLP\n",
"\n",
"The loss at each step of the training process is displayed below."
],
"metadata": {
"id": "0TF629ZDMPQ7"
}
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {
"id": "HCew0e4YnCaG",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 521
},
"outputId": "76721c14-da74-4f82-c7c5-3060b36be958"
},
"outputs": [
{
"output_type": "stream",
"name": "stdout",
"text": [
"315\n",
"100\n"
]
},
{
"output_type": "execute_result",
"data": {
"text/plain": [
""
]
},
"metadata": {},
"execution_count": 17
},
{
"output_type": "display_data",
"data": {
"text/plain": [
""
],
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAiAAAAHFCAYAAADL6EKwAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAACFRklEQVR4nO3dd3hb5d3G8a+8t504Thxn770XYSSMQAaEPQoBwl4Jo0ALtEAYbaEvlFIgzAJpKQXKCCMBQoCQhOw9nb2ns7y3fd4/jo50JMuOp2Q79+e6fMmSjs55ZNHqzu9ZDsMwDERERET8KCjQDRAREZFTjwKIiIiI+J0CiIiIiPidAoiIiIj4nQKIiIiI+J0CiIiIiPidAoiIiIj4nQKIiIiI+F1IoBtQ35SWlnLgwAFiY2NxOByBbo6IiEiDYRgGWVlZpKSkEBRUcY1DAcTLgQMHaNOmTaCbISIi0mDt3buX1q1bV3iMAoiX2NhYwPzjxcXFBbg1IiIiDUdmZiZt2rRxfZdWRAHEi9XtEhcXpwAiIiJSDZUZwqBBqCIiIuJ3CiAiIiLidwogIiIi4ncaAyIi0ggZhkFxcTElJSWBboo0MqGhoQQHB9f4PAogIiKNTGFhIQcPHiQ3NzfQTZFGyOFw0Lp1a2JiYmp0HgUQEZFGpLS0lJ07dxIcHExKSgphYWFaVFFqjWEYHDlyhH379tGlS5caVUIUQEREGpHCwkJKS0tp06YNUVFRgW6ONEJJSUns2rWLoqKiGgUQDUIVEWmETrYMtkh11VZFTf+FioiIiN8pgDhNnTqVnj17MmTIkEA3RUREakH79u15+eWXK338L7/8gsPhID09vc7aJG4KIE6TJk1i48aNLFu2LNBNERE5pTgcjgp/nnrqqWqdd9myZdxxxx2VPv7000/n4MGDxMfHV+t6laWgY9IgVBERCaiDBw+6fv/kk0948skn2bx5s+sx+3RPwzAoKSkhJOTkX19JSUlVakdYWBjJyclVeo1UnyogIiISUMnJya6f+Ph4HA6H6/6mTZuIjY3lu+++Y9CgQYSHh/Prr7+yfft2LrnkElq0aEFMTAxDhgzhxx9/9DivdxeMw+Hgn//8J5dddhlRUVF06dKFr7/+2vW8d2Vi2rRpJCQkMGvWLHr06EFMTAxjxozxCEzFxcXcd999JCQkkJiYyCOPPMLEiRO59NJLq/33OHHiBDfeeCNNmjQhKiqKsWPHsnXrVtfzu3fvZvz48TRp0oTo6Gh69erFt99+63rthAkTSEpKIjIyki5duvD+++9Xuy11SQHED15ZChf8Bz5YG+iWiMipxjAgtygwP4ZRe+/j0Ucf5fnnnyc1NZW+ffuSnZ3NuHHj+Omnn1i1ahVjxoxh/Pjx7Nmzp8LzPP3001x99dWsXbuWcePGMWHCBI4fP17u8bm5ubz44ot88MEHzJs3jz179vDwww+7nv/rX//Khx9+yPvvv8+CBQvIzMzkyy+/rNF7vemmm1i+fDlff/01ixYtwjAMxo0bR1FREWAOGSgoKGDevHmsW7eOv/71r64q0RNPPMHGjRv57rvvSE1N5Y033qBZs2Y1ak9dUReMH6TlwOZjcCQn0C0RkVNNXjH0eD0w1069B6JCa+dczzzzDOeff77rftOmTenXr5/r/rPPPsv06dP5+uuvmTx5crnnuemmm7j22msB+Mtf/sIrr7zC0qVLGTNmjM/ji4qKePPNN+nUqRMAkydP5plnnnE9/+qrr/LYY49x2WWXAfDaa6+5qhHVsXXrVr7++msWLFjA6aefDsCHH35ImzZt+PLLL7nqqqvYs2cPV1xxBX369AGgY8eOrtfv2bOHAQMGMHjwYMCsAtVXqoD4QZjzr1xUGth2iIg0VNYXqiU7O5uHH36YHj16kJCQQExMDKmpqSetgPTt29f1e3R0NHFxcaSlpZV7fFRUlCt8ALRs2dJ1fEZGBocPH2bo0KGu54ODgxk0aFCV3ptdamoqISEhDBs2zPVYYmIi3bp1IzU1FYD77ruPP/3pT5xxxhlMmTKFtWvd5fW7776bjz/+mP79+/P73/+ehQsXVrstdU0VED8IdS4UpwAiIv4WGWJWIgJ17doSHR3tcf/hhx9m9uzZvPjii3Tu3JnIyEiuvPJKCgsLKzxPaKhnScbhcFBaWv7/Ofs63qjNvqVquO222xg9ejQzZ87khx9+4LnnnuNvf/sb9957L2PHjmX37t18++23zJ49m/POO49Jkybx4osvBrTNvqgC4gchVgVEm1KKiJ85HGY3SCB+6nILmgULFnDTTTdx2WWX0adPH5KTk9m1a1fdXdCH+Ph4WrRo4bF8Q0lJCStXrqz2OXv06EFxcTFLlixxPXbs2DE2b95Mz549XY+1adOGu+66iy+++IKHHnqId955x/VcUlISEydO5D//+Q8vv/wyb7/9drXbU5dUAfGDMGcFpFgVEBGRWtGlSxe++OILxo8fj8Ph4IknnqiwklFX7r33Xp577jk6d+5M9+7defXVVzlx4kSllitft24dsbGxrvsOh4N+/fpxySWXcPvtt/PWW28RGxvLo48+SqtWrbjkkksAeOCBBxg7dixdu3blxIkTzJkzhx49egDw5JNPMmjQIHr16kVBQQEzZsxwPVffKID4gVUBKVQFRESkVrz00kvccsstnH766TRr1oxHHnmEzMxMv7fjkUce4dChQ9x4440EBwdzxx13MHr06Ept0jZixAiP+8HBwRQXF/P+++9z//33c9FFF1FYWMiIESP49ttvXd1BJSUlTJo0iX379hEXF8eYMWP4+9//DphrmTz22GPs2rWLyMhIzjrrLD7++OPaf+O1wGEEujOrnsnMzCQ+Pp6MjAzi4uJq5Zxvr4Q/z4fLusPLo2vllCIiPuXn57Nz5046dOhAREREoJtzyiktLaVHjx5cffXVPPvss4FuTp2o6L+xqnyHqgLiB6HOCoi6YEREGpfdu3fzww8/MHLkSAoKCnjttdfYuXMn1113XaCbVu9pEKofhKoLRkSkUQoKCmLatGkMGTKEM844g3Xr1vHjjz/W23EX9YkqIH4QqkGoIiKNUps2bViwYEGgm9EgqQLiB6GahisiIuJBAcQPtBCZiIiIJwUQP9BCZCIiIp4UQPxAe8GIiIh4UgDxgxB1wYiIiHhQAPEDDUIVERHxpADiB1qITESk7p199tk88MADrvvt27fn5ZdfrvA1DoeDL7/8ssbXrq3znEoUQPzANQtGFRARkTLGjx/PmDFjfD43f/58HA4Ha9eurfJ5ly1bxh133FHT5nl46qmn6N+/f5nHDx48yNixY2v1Wt6mTZtGQkJCnV7DnxRA/EDTcEVEynfrrbcye/Zs9u3bV+a5999/n8GDB9O3b98qnzcpKYmoqKjaaOJJJScnEx4e7pdrNRYKIH4QqlkwIiLluuiii0hKSmLatGkej2dnZ/Ppp59y6623cuzYMa699lpatWpFVFQUffr04aOPPqrwvN5dMFu3bmXEiBFERETQs2dPZs+eXeY1jzzyCF27diUqKoqOHTvyxBNPUFRUBJgViKeffpo1a9bgcDhwOByuNnt3waxbt45zzz2XyMhIEhMTueOOO8jOznY9f9NNN3HppZfy4osv0rJlSxITE5k0aZLrWtWxZ88eLrnkEmJiYoiLi+Pqq6/m8OHDrufXrFnDOeecQ2xsLHFxcQwaNIjly5cD5p4248ePp0mTJkRHR9OrVy++/fbbarelMrQUux9oEKqIBIphGOTm5gbk2lFRUTgcjpMeFxISwo033si0adP44x//6HrNp59+SklJCddeey3Z2dkMGjSIRx55hLi4OGbOnMkNN9xAp06dGDp06EmvUVpayuWXX06LFi1YsmQJGRkZHuNFLLGxsUybNo2UlBTWrVvH7bffTmxsLL///e+55pprWL9+Pd9//z0//vgjAPHx8WXOkZOTw+jRoxk+fDjLli0jLS2N2267jcmTJ3uErDlz5tCyZUvmzJnDtm3buOaaa+jfvz+33377Sd+Pr/dnhY+5c+dSXFzMpEmTuOaaa/jll18AmDBhAgMGDOCNN94gODiY1atXExoaCsCkSZMoLCxk3rx5REdHs3HjRmJiYqrcjioxxDAMw3jttdeMHj16GF27djUAIyMjo9bOvSfDMNq+bBhdX6u1U4qI+JSXl2ds3LjRyMvLMwzDMLKzsw0gID/Z2dmVbndqaqoBGHPmzHE9dtZZZxnXX399ua+58MILjYceesh1f+TIkcb999/vut+uXTvj73//u2EYhjFr1iwjJCTE2L9/v+v57777zgCM6dOnl3uNF154wRg0aJDr/pQpU4x+/fqVOc5+nrffftto0qSJx/ufOXOmERQUZBw6dMgwDMOYOHGi0a5dO6O4uNh1zFVXXWVcc8015bbl/fffN+Lj430+98MPPxjBwcHGnj17XI9t2LDBAIylS5cahmEYsbGxxrRp03y+vk+fPsZTTz1V7rXtvP8bs8vIyKj0d6i6YJwmTZrExo0bWbZsWa2fO0wVEBGRCnXv3p3TTz+d9957D4Bt27Yxf/58br31VgBKSkp49tln6dOnD02bNiUmJoZZs2axZ8+eSp0/NTWVNm3akJKS4nps+PDhZY775JNPOOOMM0hOTiYmJobHH3+80tewX6tfv35ER0e7HjvjjDMoLS1l8+bNrsd69epFcHCw637Lli1JS0ur0rXs12zTpg1t2rRxPdazZ08SEhJITU0F4MEHH+S2225j1KhRPP/882zfvt117H333cef/vQnzjjjDKZMmVKtQb9VpQDiB9ZS7CUGlBqBbYuInFqioqLIzs4OyE9VB4DeeuutfP7552RlZfH+++/TqVMnRo4cCcALL7zAP/7xDx555BHmzJnD6tWrGT16NIWFhbX2t1q0aBETJkxg3LhxzJgxg1WrVvHHP/6xVq9hZ3V/WBwOB6WldTdY8KmnnmLDhg1ceOGF/Pzzz/Ts2ZPp06cDcNttt7Fjxw5uuOEG1q1bx+DBg3n11VfrrC2gMSB+EeoOuBSVQLj+6iLiJw6Hw+Nf4vXZ1Vdfzf33389///tf/v3vf3P33Xe7xoMsWLCASy65hOuvvx4wxzxs2bKFnj17VurcPXr0YO/evRw8eJCWLVsCsHjxYo9jFi5cSLt27fjjH//oemz37t0ex4SFhVFSUnE5u0ePHkybNo2cnBzX337BggUEBQXRrVu3SrW3qqz3t3fvXlcVZOPGjaSnp3v8jbp27UrXrl357W9/y7XXXsv777/PZZddBkCbNm246667uOuuu3jsscd45513uPfee+ukvaAKiF+E2v7KWoxMRMS3mJgYrrnmGh577DEOHjzITTfd5HquS5cuzJ49m4ULF5Kamsqdd97pMcPjZEaNGkXXrl2ZOHEia9asYf78+R5Bw7rGnj17+Pjjj9m+fTuvvPKKq0Jgad++PTt37mT16tUcPXqUgoKCMteaMGECERERTJw4kfXr1zNnzhzuvfdebrjhBlq0aFG1P4qXkpISVq9e7fGTmprKqFGj6NOnDxMmTGDlypUsXbqUG2+8kZEjRzJ48GDy8vKYPHkyv/zyC7t372bBggUsW7aMHj16APDAAw8wa9Ysdu7cycqVK5kzZ47rubqiAOIHHhUQBRARkXLdeuutnDhxgtGjR3uM13j88ccZOHAgo0eP5uyzzyY5OZlLL7200ucNCgpi+vTp5OXlMXToUG677Tb+/Oc/exxz8cUX89vf/pbJkyfTv39/Fi5cyBNPPOFxzBVXXMGYMWM455xzSEpK8jkVOCoqilmzZnH8+HGGDBnClVdeyXnnncdrr71WtT+GD9nZ2QwYMMDjZ/z48TgcDr766iuaNGnCiBEjGDVqFB07duSTTz4BIDg4mGPHjnHjjTfStWtXrr76asaOHcvTTz8NmMFm0qRJ9OjRgzFjxtC1a1def/31Gre3Ig7DMDQqwSYzM5P4+HgyMjKIi4urlXMaBnR4xRwWvuw2aN4wqqEi0gDl5+ezc+dOOnToQERERKCbI41QRf+NVeU7VBUQP3A43FUQdcGIiIgogPiNFiMTERFxUwDxkxAtxy4iIuKiAOInYdoRV0RExEUBxE+sCojGgIiIiCiA+I01CLVQAURE/EATHKWu1NZ/WwogfqJBqCLiD9by3oHaAVcaP2tpevs+NtWhRcH9JFRdMCLiB8HBwSQkJLg2NYuKinItZy5SU6WlpRw5coSoqChCQmoWIRRA/MTVBaMKiIjUseTkZIBq76wqUpGgoCDatm1b42CrAOInGoQqIv7icDho2bIlzZs3p6ioKNDNkUYmLCyMoKCaj+BQAPET1zRcBRAR8ZPg4OAa99OL1BUNQvWTEA1CFRERcVEA8ZNQrYQqIiLiogDiJ6FaCVVERMRFAcRPVAERERFxUwDxE1VARERE3BRA/EQLkYmIiLgpgPiJ9oIRERFxUwDxE9dCZOqCERERUQDxl7hw8/aI9ocSERFRAPGXXknm7YYjgW2HiIhIfaAA4ie9nQFk01HNhBEREVEA8ZO28RAXBgUlsPV4oFsjIiISWAogfuJwQM/m5u/rtUO2iIic4hRA/KhXM/N209HAtkNERCTQFED8qF2CebsvK6DNEBERCTgFED9qHWfe7ssMbDtEREQCTQHEj1rHmrcKICIicqpTAHGaOnUqPXv2ZMiQIXV2jVbOCkhGAWQW1NllRERE6j0FEKdJkyaxceNGli1bVmfXiAmDJhHm7/tVBRERkVOYAoifWeNA9msgqoiInMIUQPyslXMcyF5VQERE5BSmAOJnmgkjIiKiAOJ3CiAiIiIKIH637rt/cvjVkSz86p1AN0VERCRgFED8rPDEPgq2z+NA6pJAN0VERCRgFED8bNiA3gBk71tPdmGAGyMiIhIgCiB+NsQZQIoObWBvemmAWyMiIhIYCiB+1rlzZxwhYRgF2axI3R3o5oiIiASEAoifhYSE0KRNDwCWr1kf4NaIiIgEhgJIALTuZHbDbNigACIiIqcmBZAA6NTdDCC7tyiAiIjIqUkBJAB69zYDSNpOBRARETk1KYAEwKD+ZgDJ3L+JoqKiALdGRETE/xRAAqB/t7Y4wmMwigvZunVboJsjIiLidwogAdAyNojQ5F4AvDZzPRkFAW6QiIiInymABEBYMMS26QPAhz+t55m5AW6QiIiInymABEhSB+eKqAfX88MOKCoJcINERET8SAEkQFp1cgeQzAJYdiDADRIREfEjBZAAyW9qBpDio9soLczjxx0BbpCIiIgfKYAEyIiezQmKbgZGKcVpm/hxJxhGoFslIiLiHwogAfKHsxx06mZWQYzD69mdAVuPB7hRIiIifqIAEiAxYTD6dDOANMs2V0RVN4yIiJwqFEACyFqS3ZG2DoA1hwPZGhEREf9RAAkgK4Ac2mFWQLILA9kaERER/1EACaBevczVUI8e3EtpXoYCiIiInDIUQAIoISGB1q1bA1B0aAPZ2pdOREROEQogAWZ1wxQdXK8KiIiInDIUQALMCiCFB9eRowAiIiKnCAWQAOvfvz8AhftWkl2oxchEROTUoAASYEOHDgWgaN9KSkuKyNU4EBEROQUogARY586dadKkCUZRPkUH1mogqoiInBIUQALM4XC4qiAFu5dqHIiIiJwSFEDqgWHDhgFQuHuJZsKIiMgpQQGkHnBXQBRARETk1KAAUg9YAaQ4bRNpxzMC3BoREZG6pwBSDyQlJRHToiMAq1YsC3BrRERE6p4CSD3RoptZBdm4akmAWyIiIlL3FEDqiTY9zIGovy5eypGcADdGRESkjimA1BPte5sVkLTNS7j3Oy2HKiIijZsCSD3RuecACAqhNOsw89ftCXRzRERE6pQCSD0RFhFJWKt+ABTuWcrR3AA3SEREpA4pgNQTmQUQ1ta9HkjqkQA3SEREpA4pgNQTdw6Ctr3cK6JuOBrgBomIiNQhBZB6onUcfP5bZwDZu4L1h4oD3CIREZG6owBSj3Tt2pXo2HiMojyWr14f6OaIiIjUGQWQeiQoKIhBg4cAsG3tEvJVBBERkUZKAcRp6tSp9OzZkyFDhgS0HWecZg5Ezd+1hC3HAtoUERGROqMA4jRp0iQ2btzIsmWB3YvltNOscSDL2aCZMCIi0kgpgNQzgwcPBqDo0AbW7NWa7CIi0jgpgNQzKSkpNElqCUYpPy9ajaFV2UVEpBFSAKmHThtmjkPZun45aw4HuDEiIiJ1QAGkHho+1OyGKdyzjI83BLgxIiIidUABpB6yxoEU7l3OurQAN0ZERKQOKIDUQ1YAKU7bzIn0zAC3RkREpPYpgNRDSUlJtGrTDoC0rSsD3BoREZHapwBST/UfaFZBjm9fppkwIiLS6CiA1FNDh5gBpGDPcnKLAtwYERGRWqYAUk+d7pyKW7h3OZkFAW6MiIhILVMAqacGDRoIQPGxHew+qE1hRESkcVEAqaeaNGlCRPPOACxbviLArREREaldCiD1WNNO5jiQ1SuXB7glIiIitUsBpB5r0dUcB7J+dWB36BUREaltCiD1WJseZgVk63pVQEREpHFRAKnHOvQYAA4HJw7v49ChQ4FujoiISK1RAKnHkprEEtK8OwArVmggqoiINB4KIPVYXDiEtzXHgSxbpnEgIiLSeCiA1GNx4RDWxhwHogAiIiKNiQJIPWYPICtWrMDQpjAiItJIKIDUY/HhENqqHziCOHz4MAcOHAh0k0RERGqFAkg91i4BgsKiCEvuCWggqoiINB4KIPVY2zgIDYLQ1oMAzwDy807YcCRQLRMREakZBZB6LDTYrIKEtfEMIHsy4Oav4a6ZAWyciIhIDSiA1HOdm5QNIOvSzOeO5QaqVSIiIjWjAFLPdW4Koa364wgK4tChQ+zdd4Ctx8znCksC2zYREZHqUgCp5zo1NQeiRrbsAcCtb61gy3HzuaJSKNXMXBERaYAUQOq5Lk3MW0eK2Q2zZNkKthxzP68qiIiINEQKIPVcR2cACXPOhCnct4IdJ9zPK4CIiEhDpABSz0WHQUqMeyBq0d4VlNi6XRRARESkIVIAaQCsgag4gijJPEhJxkHXcwogIiLSECmANAAdm0BQeDShLboDZjeMRQFEREQaIgWQBiA6zLy1VkQt3KsAIiIiDZsCSANwemvz1hoHYg8gBQogIiLSACmANABntoU3xsG157tnwoQHm8+pAiIiIg2RAkgDMa4LXHFuf3A4KMk4QFLpIUABREREGiYFkAbkjE4xxLUyB6Lm7zG7YRRARESkIVIAaUAiQuDis81umJzdZgA5nA3LD8DifXAiL5CtExERqTwFkAZm0CAzgGTuMgPI736EKz6Faz6HCz8CQ3vDiIhIA6AA0sAMHjwYgPTtyzCcacPhfG5/FuQWBahhIiIiVaAA0sAMGjSI0NBQ8k4cpPjYDgBaxECwM4VkFQawcSIiIpWkANLAREZGMnToUAAKts0FIDoUYpyLlSmAiIhIQ6AA0gCNHDkSgILt8wAzgMSGm89lFQSqVSIiIpWnANIAjRgxAoD87WYFJCoMYp0VkGxVQEREpAFQAGmATj/9dBxBwZQc30XxiT1EhbgDiLpgRESkIVAAaYBiY2Np2XUgYHbDRIepC0ZERBoWBZAGqmN/cxxI/vZ5RGkQqoiINDAKIA1Ul4HmOJCCbXPNQahWAFEFREREGgAFkAaq64AzweGg+MgWSjIPaRCqiIg0KAogDVRCkyaEtuwLwP5181xjQDIVQEREpAFQAGmgwoMhvLM5DmTX2nmuMSCqgIiISENQowCyd+9efv75Z3Jzc12PlZaW8te//pUzzjiDUaNGMXPmzBo3UsoKC4aITuY4kK0r52oWjIiINCghNXnxE088wTfffMOhQ4dcj/35z39mypQprvtz585l4cKFDBkypCaXEi9hwRDuDCB7t67HyD4KNFMFREREGoQaVUAWLFjAqFGjCA0NBcAwDF577TW6d+/Onj17WLp0KdHR0bzwwgu10lhxCwuG4JgkQlr0AGDb6l8BTcMVEZGGoUYBJC0tjXbt2rnur169miNHjnDvvffSunVrBg8ezKWXXsqyZctq3FDxFBZs3kZ0MseBbFhuLsueqS4YERFpAGoUQEpLSyktLXXd/+WXX3A4HJx77rmux1q1auXRRSO1wwogVjfMqsXmxnTqghERkYagRgGkbdu2LF261HX/yy+/pGXLlnTr1s312KFDh0hISKjJZcSHcCuAOGfCbFi7iqIj28grhqKSADZMRESkEmoUQK644goWLFjAlVdeyfXXX8+vv/7KFVdc4XHMxo0b6dixY40aKWVZFZCQ+BTOvWAshmGQ8+tUAI7nB7BhIiIilVCjAPLwww8zZMgQvvjiC/773//Sp08fnnrqKdfzu3fvZunSpZx99tk1bKZUZNLk+wDIXvIepflZHMkJcINEREROokbTcOPi4li8eDHr168HoEePHgQHB3sc88UXXzB48OCaXEZ8KHIPvWH82Avo2rUrW7ZsIWfZvzl6zaTANUxERKQSamUl1N69e9O7d+8y4aNdu3ZccskltGrVqjYuIzaG4f49NCSIe++9F4Csea+Qll1azqtERETqhxoFkKysLHbs2EFRUZHH45988gkTJkzgtttuY9WqVTVqoPg2tBX0bAaXdTfvT5w4kbCoOIqPbGHezz8EtnEiIiIn4TAM+7+lq+buu+/mP//5D4cPHyYqKgqAN954g8mTJ2OdNjIykhUrVtC9e/faaXEdy8zMJD4+noyMDOLi4gLdnAoZBjgc7vtnXP1bFn76Ml2GjWXL4m8D1zARETklVeU7tEYVkLlz5zJq1ChX+AB4/vnnadWqFfPmzeN///sfhmFoJdQ6Yg8fAGMnTAKHg61LvmPLli2BaZSIiEgl1CiAHDx4kA4dOrjup6amsnfvXu677z7OPPNMrrzySi6++GLmzZtX44bKyfXs1pmInhcC8NprrwW4NSIiIuWrUQApKCggLCzMdX/u3Lk4HA4uuOAC12MdO3Zk//79NbmMVFLzKIgdYU7Jff/998nIyAhwi0RERHyrUQBp3bo1a9eudd2fMWMGTZs2pW/fvq7Hjh07RkxMTE0uI5XULAoiuo4iPLkH2dnZTJs2LdBNEhER8alGAWTs2LH88MMPPPzwwzz++ON8//33jB8/3uOYLVu20LZt2xo1UiqnWRQ4HA6izjKrIK+++qrHXj0iIiL1RY0CyGOPPUbbtm156aWX+Mtf/kKLFi145plnXM+npaWxYMECRowYUeOGysk1jYTYMIgefAMxsXFs376duXPnBrpZIiIiZdQogCQnJ7Nhwwa+/vprvv76a1JTU2ndurXr+aNHj/LCCy9wxx131LihcnJBDujdHILCoxk6+hoA/v3vfwe4VSIiImXVaB2QxqghrQPiy19+hbdWwEh+5YMHziImJoZDhw4RHR0d6KaJiEgjV5Xv0BrtBWO3f/9+Vq9eTWZmJnFxcfTv319LsAdA3+bm7YnmZ9ChQwd27tzJl19+yYQJEwLbMBEREZsa7wWzbds2zj//fNq2bcvFF1/M9ddfz8UXX0zbtm254IIL2LZtW220UyqpbwvzdtMxB5dcfSOgbhgREal/atQFs3fvXoYMGUJaWhrdu3dnxIgRtGzZkkOHDjFv3jxSU1Np0aIFS5cupU2bNrXZ7jrT0LtgDAMu+hjWp0Hzgh0sf6QTQUFBbN2xh47tVJESEZG647el2J9++mnS0tJ4/fXX2bBhA2+++SZTpkzhjTfeYMOGDbzxxhscPnzYY2aM1C2HA94bD23jIS28I1GdzqS0tJQRD/6XrIJAt05ERMRUowAya9Ysxo8fz1133YXDe2MS4M4772T8+PF89913NblMtVx22WU0adKEK6+80u/XDrQWMfDfyyElBiIGm90waQv/RepRjTcWEZH6oUYBJC0tjd69e1d4TO/evTly5EhNLlMt999//yk99qFNHEy/Bs4ccxWEhFN0aAO/LlkNQFEJnMhzH7vtOPxnLZRozTIREfGTGgWQpKQkNm7cWOExGzduJCkpqSaXqZazzz6b2NhYv1+3PkmOga9uSqDL6ZcAMONTM5Dd/S0MfRf2ZZrHPfkL/HEO/Lizetc5ngeP/AhrDtVCo0VE5JRQowAyevRovv76a959912fz7/33nt88803jBkzpkrnnTdvHuPHjyclJQWHw8GXX35Z5pipU6fSvn17IiIiGDZsGEuXLq3OWzglnDXe7IZZ8v2HFBUVsfYwFJbAamdg2J1u3m5Iq975754JH2+AO2fWvK0iInJqqFEAmTJlComJidxxxx306dOHyZMn8+yzzzJ58mT69u3L7bffTtOmTZkyZUqVzpuTk0O/fv2YOnWqz+c/+eQTHnzwQaZMmcLKlSvp168fo0ePJi2tmt+gjdzZ511AUGwLctOP8Pnnn5Oebz6+OwNKDTiUY97fdKx651/s3Oz4YHbN2yoiIqeGGi1E1rZtWxYsWMCdd97JL7/8woYNGzyeP+ecc3jzzTerPAV37NixjB07ttznX3rpJW6//XZuvvlmAN58801mzpzJe++9x6OPPlqlaxUUFFBQ4J4ekpmZWaXXNwTtm4YSe+YkMr57kr/+9f/In3gNDoeDPRlwNBeKnWM/tlQjgFhhBqBTk9ppr4iINH41XoisS5cu/Pzzz+zevZuvvvqKDz74gK+++ordu3fz008/8cUXX3DeeefVRlsBKCwsZMWKFYwaNcr1WFBQEKNGjWLRokVVPt9zzz1HfHy866ehrFdSFSlxEHPmPTjColi9ehUFW38GzArIIVvVYlc65BdX7dwL9rp/j4+oeVtFROTUUGtLsbdp08bnl/emTZv45ZdfausyHD16lJKSElq0aOHxeIsWLdi0aZPr/qhRo1izZg05OTm0bt2aTz/9lOHDh5c532OPPcaDDz7oup+ZmdnoQkirWAiOTiR62K1kz3+VzJ/+j4iu57Enw7PbxAC2Hoc+zSt/7r22glFVw4uIiJy6ai2A1Dc//vhjpY4LDw8nPDy8jlsTWBEh0CwSis9+kNyFr5O/+QcK96/hQKt+7MnwPHbLsaoFkIJi37+LiIhUpMZdMP7WrFkzgoODOXz4sMfjhw8fJjk5OUCtqv9axUFIYnu6nHUVAJk/v4ABLD/gedzmKo4DKSix/a4AIiIildTgAkhYWBiDBg3ip59+cj1WWlrKTz/95LOLRUwpziVREkf9DoDcVR9TfHw3S5wzWNrGm7ebj1btvPbQoS4YERGprHoZQLKzs1m9ejWrV68GYOfOnaxevZo9e/YA8OCDD/LOO+/wr3/9i9TUVO6++25ycnJcs2KkrFbOALI/ZiDhXc+D0hKy5r7MCecslpHtzFv7TJhl++G2bzzHeXizV0DyS8o/TkRExK5ejgFZvnw555xzjuu+NUh04sSJTJs2jWuuuYYjR47w5JNPcujQIfr378/3339fZmCquLV2bkpoAHHn/p4jW34ie9E7xF3wOMHRiZzfET5YCweyIbMA4sLhys/M16Tnw2dX+T6vKiAiIlIdVQ4g48aNq9Lx69atq+olOPvsszGMijdOmzx5MpMnT67yuU9VrWyr0kd0O5/INgPI27uKjBl/oOk1bzGoJbSMMWfFbD4GQ1Lcx1fULWOvgBSXmj8h9bKuJiIi9UmVA8j3339f5Yv42ilX/CvFFkAcDgdn3fkyPzw+kuxFb9P+7InEhJ1O56ZmANmV7hlACiroWvEeeJpfDDFhtdp0ERFphKocQHburOaOZRJQVheM5fxzR7Bg6M3kLH2fff+9i6KnV9A0MhTwXN0UzH1jyuMdThRARESkMqocQNq1a1cX7ZA6Fh8O0aGQU2Te79kMEi7+P/I2fE367nW8/PLLNBlizpA54RVAKuoM81UBERERORn11p8iHA64sIv7fvNoCI5pRsLFLwDw1FNPUXpiNwAZ+b7O4JuvCoiIiMjJKIA4TZ06lZ49ezJkyJBAN6XOPH8ePHoGXN0T+ifDg6dBnwtuYvgZI8jNzWXGy/diGAbp+WWDRHndMAogIiJSHQogTpMmTWLjxo0sW7Ys0E2pM8FBcPdgeOF8c6bK/cPgl5sc/PPtNwgNDWX1vG/I+uXvpOebU3HtjuWat96Tk9QFIyIi1aEAIvTs2ZNnnnkGgPSvHmLlFy+R4RVAjuTC7B0w8B34yTYOWRUQERGpDgUQAeCRRx7h9t8+AcCmDx/i9X/8zeP5I7nmqqjH8+CWr92PWxUQa+0P7QcjIiKVoQAigLk2yGNPPEPc6CkAvPzMw2T+/ILr+aO5vl9nVUDinRsK55fAngw44314Z2VdtlhERBoyBRBxaRIJCWOfIn7MUwCkf/17Mn/8K1BBAHFWPFwBpBj+8ivsy4Q/za/jBouISIOlACIusWHgAOLHTGH0bU8DkD7jUTJmPVtmUGpGgTkg1VUBiTBv84vhcI7/2iwiIg2TAoi4BAeZm9AB9LjySeIv/DMAGd89yRevP+mxP8/NX8H2E1DqfCjOVgHJLqx5W0oNKCmt+XlERKR+UgARDwnOSsaeDIg//w8kXmKOA1n+0bNkzPiDK4SsOAgvLHS/zt4Fk+VVLakqw4ArP4XzPoCiCpaBFxGRhksBRDw0sQJIpnnb57KHSbj07wBk/vQ8xz++DaPIXCp1wV7368qrgFRnWm6JYQacnemw7XjVXy8iIvWfAoh4sMZypDnHcbSOg7izH6DJlVPBEUTOkvc4/OpIitP3u/aVCQ8G5z52ZBd6BhDv9UQqw171qGgnXhERabgUQMSD1ZViaePcRTf2zHtIuvM7ImKbULhnKYf+Nojc7b8CZgCJcG5ruCvdc/O6quwrYylUABERafQUQMRDnFcAaR3n/j2y+wX8btoy+vTpQ2nWYdJeO4eM758mtCSXiGDzmC1eXSbes2cqwx5A8oqq/noREan/FEDEg9UFY2kT73m/b/dOLFq0iDanXwOlxWR8/xQbnuzGmtn/xTAM9mV6Hl+tLhjb7JccBRARkUZJAUQ8eFdA2sR53k+OgejoaCY8/RGJEz8huEk7Ck/s45+PT+Dwy6dTsGsJA1u6B7PWtAJS0xk1IiJSPymAOE2dOpWePXsyZMiQQDcloLzHgDSPhrBg9/2UWPO2Y1MH0QOupuVjqXS56s9ER0dTuHsxh18+jWaz72Bg0yygahWQR3+Cp+d6BpDy1hR5ZSmM+2/1Ao6IiASeAojTpEmT2LhxI8uWLQt0UwLKuwISHw5xYe77LWPM245NzNugsEh6XP4HtmzZwk033QTAP//5Dl/c14/87fMrHRCO5cJH6+G91Z6horwA8vF62HDEnK5bV7Yc0+6+IiJ1RQFEPNgrIMEOiAp1jwtJiHBPt+3UxH1ceAikpKTw/vvvM2fOHNq1a0fGoZ2kvTaS//39d+Tnn3wqjD1oHM9z/57lI4AYhrk7r/extWnlQTj/P/D7H+vm/CIipzoFEPFgDyBx4eBwuKsiVvUDzNkxoc7/esJtXTRnn302a9eu5bTxt4BhsODjFxk8eDArV1a8NW62bbDpMVuo8FUBySxwd9Mcq6MAknrUvN2dXjfnFxE51SmAiIe48LK/+wogIUHQLsH8PTzE6xxxcdz97Ls0u+1rIhOas2HDBoYNG8YzzzxDUZHvaS05tqBxzLbzrj2AvLwYbpgO+7Pcjx0vZ5femjriXIhNXTAiInVDAUQ82KfhRju7W6yqiDUA1WJ1w9grIPbzRPUezwV/28D4y66kuLiYKVOmcPrpp5Oamlrm+Mp0wfx9CczbA/9a436sriogVhePAoiISN1QABEPMWFlH7PWAunc1PPxDgnmrXcFBKCVM6wcKG3G6Q/+j8QbPsQRmcDy5csZMGAAL774IiUl7ukuOVXogtlxwv17XY0BcQUQrcQqIlInFEDEQ4iP/yImDYb3xsN1vT0fv7Qb9GkOF3ct+5puiebt4RzYn+UgetB1tHxkPWPGjKGgoIDf/e53jBw5kq1btwLlV0B8BZADti6YuqqApKkLRkSkTimAyElFh8F5HctWOnokwYxr4ez2ZV8TG+5exGzVIfM2JKEV3377Le+88w6xsbEsWLCAfv368corr5CV717+9KiPAGLfoM5jDIi6YEREGiQFECmXcfJDKtSjmXm717Y8e6nh4LbbbmPdunWce+655OXlcf/99/P8rSMoOrwZ8D0GJM8WBOztqosAYhieg1CNmv4hRESkDAUQqTPdm5V9zBrr0a5dO2bPns3UqVOJiYlh59oFHHyhH5k//pVj2e60kV1oBoDyKhFZhVBQy1WKrELPXXi1I6+ISO1TAJFy9W5es9f7DCC2MR1BQUHcc889rF+/ng6DR0NxAekzHmXPi8Mo3LsCgFIDcosq7go5cfJ1zqrkiNfU3toOOCfz0w64fjocyvbvdUVE/EkBRMqYcS3c0h+eOKtm5+nhI4Bk+1gGJKFFO8578juaXjcNR2QCRftWcuiloZz44gFK87PIKqw4gNT2QFRrAKolz88B5JZvYP4emPStf68rIuJPCiBSRp/mMGWk55og1dEuHiK8Bq7meM1q2XkCzpoGP+xwEDN0Iil/2ETUoOvAKCVr3j84+FwPPvnfZ+QWluKtebR5W9nFyEpKYfUh87YiR7wCSKAGoi6vw31uREQCTQFE6kxwEHT1WjvEPq22qAQemOW5Y25wbAua3fAhSXfNIqRZJ0oy9vPArVdx1bn9yVn5MUapOSAjNMi9IV55FZBD2fDBWrMLB+C5BXDJJ54Lmfni3QXj7wCSYAt+/u7+ERHxFwUQqVPe40DsC469uhRWH/b9usjuF5D8+3XEjX6SyOhYtm1ax7F/X8vB53qSveR9moYV0SzSPLa8mTDXfg6Pz4HnfjXvv+PcjubZ+RW3OdAVkNZx7t/XlPP3ERFp6BRAnKZOnUrPnj0ZMmRIoJvSqHiPA7G6YHalw2vLzN/jfKy+ChAUFknC2Kd5edZubnjgGYKimlJ8ZAvHP7qFtY+1Z8lb95C38TsOpZujULefMKsb1kZ1O9LN2++2eXb92L/gfQl0BaTQNuvG2hRPRKSxUQBxmjRpEhs3bmTZsmWBbkqjMiTF877VBfPvtVBiwMh2MLpTxecoDG3CFXc9QcqU3SRc8iJBcckUnDjAiq/f4Mjb43hqXCJXXnkl9/xzFU/+Ag/94Pn6olJYUYXxFIEOIPZul1zfe/eJiDR4CiBSp/q0gG9+A+d3NO/nFEFeEXy6wbx/c39om1DxOU7kmyEgKDyGuHMeotUTO7nyTzM456q7CI5vRVF+Lp9//jk//H4gRz+4ni8W7fLolikqgSX73fcPZpnTe8sT6C4YewUkRwFERBopBRCpc31buHfSzS6EZQcgsxBSYswKSNtyukSswZjp+Z5TYR2hEQw/90Ie+vMbpDy1l/P+upLrrrsOgNwVH3LgL9244a6HKMk+ApgVEGs5eOu+d8iwsyog1vX9XgGxBZBcH3vhiIg0Bgog4hfWLrs5Re7ukGGtIcjhnk4LEB7s/r2F83GrAmKXFA1NI8HhcFCaPIAPP/yQQU8tJ7zLuVBSyLf/fokDz3Qg/ZvHyMs8xjqvwZz7svCppNQ9q8bayyaQXTCqgIhIY6UAIn4RE2reZhfC8gPm74Namrf2gapJUe7fm9sCiPd01KQoSHTOgrECQ2jrQTS/50eS7vyOZp0GYhTmkPnT8xx4pj17pj9OaP4xBjqvuT8Tn47lmd0zQQ5o5aza5Pt5KXZ7F4zGgIhIY6UAIn4R7ayAZBa4u0OsANIkEmZfD/MmmrvoWqwAkp5XtgqREmtWQMDsoikuNbtpHA4HkT3G0PPx5TS79UtCW/XHKMgmc/af2TWlLbs+/i3F6fs4UE4FxFoFNTHS3ebKVEB+2eUOVjVRUmp2EVkUQESksVIAEb+wumAW7jW7FWLCoFui+/muidAuAWJtU3KbO6shx21jQHolwUPDzdVam0SAw3nsiTzPcSK7MhxE9bmE5IdX0uyWLwhtPZCSglxWT3+ZA8925K0pt7Jp06Yy7bTGfyRFQ4SzOyizAH43G2Zu9f3eMvLhlq/hpq/MIFQThV7VFnXBiEhjpQAifhHt7ILJcg6qvGOguVKqN3sFpEWMeZuR764EjOkM9w0Fh8N8vTVQ9JiPKgmYFZGovpeR/NByprzzPV0GjoSSIlZ/+x49e/ak39mXMfOnRa7jrcGpSVHuZeTn74b/bYT/W+D7vR3OMacUZxXCwWyzHdUdN+IdQFQBEZHGSgFE/CLGVtkY39UMEb54VECcXTAGcNi5M6z33jJWN8x+W5eKNTbEzuFwcNOVo3nmX7/Q4v6FtBl6MYZhsHbul1w06nRGjBjBt99+S1qOOT+3uS2AHHaGkj2ZZQMCeC4lv+sEjP4PDHwbpi4Do4Lpvr54jzdRBUREGisFEPGLbolmuDitFbx4vlnB8CXOVgGJDHEHEmtr+ohgz+OTnCFlT4bntbzFh5ub4yVEQHiH4Qx66CsmvLWR6GG3QHAo8+fP58ILL+RP1w0gZ9X/SIwoIdwZQI46u2VKDc/rWDLz3b+vPgy7Mszg8H8L4eMNvt9nebwH22oarog0Vgog4hdJ0bD8dvj4irJVDDt7F0xYsLuL5aAzgESGeh7f0tlNs+OE+zWdvDbAA+jXwgw91vky8qFr9x4kXvsuKU/spMX5DxEWGc3h7Ws49q9r+MeNPVn02auUZB+hxFbF2Jle9tzptgqIfb0RgCm/wKYqLKdeoAqIiJwiFEDEbyJCyq98WOz7woQGmwNNwd3N4R1eUrwCSEQItI8ve97+yeatPYDkO7/cQxJaEX7hiyQ9vpu40VMIimrC4d1b+OTF+9j/ZApH3rmY3NWfYRTlu65jl2GrgFgBpGMCnN3ODBSTvjNnt1SGxoCIyKlCAUTqFXsFJDTInKJr5x1AWjrX6rCCQWQItE9wP9+5KdzY1/wB2+qqBe5ZM78bDg8Ph+DoRBLGPkXKk7t58JlX6NhzEJQWk7fhG45Ou4p9T7bk7Wcnk5qa6tEG+xgQawn4xCh46QKzvduOm90ylWF1wVhdUUWlvsedVFVBMTz4A3xZduKPiEhAKIBIvWIfhGrvgrFEllMBOWAbpNouwf38oJbw7DnusSLW+YptK57GhsO4Lu7XBEXEcs/ke3npi+W0fHQDcec9SnBCa4y8dFZ+Ze6afP755/PVV19RXFzsEUAsTSPNEGItZpZWztLv762CSz8x1zIBdxdME9v7zquFKsinG+HzVLh/Vs3PJSJSGyrojRfxP+8xIE29KiDh5VRALJEh5hLqDszZM/bZN2AGlPBg84v+oC20eO9H0zzKPFdock8Sxj9H/IV/In/rzxQtmkrm2m/48ccf+fHHHwkJCSEqsTUFMe0IadqOiG4XEDXoOppGmn1NSdGw/UT5AeSDtbAj3dwsb3Qnd7UjOsx8/4Ul5jiQ+Ajfr6+s4/knP0ZExJ9UAZF6xV4BCQ3yrASAjzEg3gEk1DzGejzWK4CA+8vcmlkTGWKONwm1/a8hJszz2o6gYCK7nU/cTV/yzeLtxJ33CMHRiRQXF5N5eBcF2+eSs+zfHPvP9Rz/5A7iQszpK9Ziar4CiGG4KzfWOBKrCyY82F3tqY2BqCEnGXsjIuJvCiBSr9in4Yb66IKJ8woU8eGe3TJWQGnnHIjqXQEB9zkznV0n1swa+7UdDmgWhU+HQtqTMP55Up49zNKNexn59K8k3vAhsWc/CI4gchb/k389eD5Hjx51df1YAeTFRXDVp+ZCZRkF7gXL1hw2u0mscSnhIe7F26o7Fdcw4Ked5hoqIcEnP15ExJ8UQJymTjX79ocMGRLoppzSvMeA2KsQoUHQyqurxOFwT8UFdxi5tLs5PuT0NmWvkRDued9aW8S7WpLoFUCsIsLaNOf9oGDSw1sT0uEMogddR58b/0bS7d/giIhjy8p5DBkyhKxtCynNTedwtjmX99WlsPQAfLsNDtoWT/vPOnh4Nny3zbwfHgxRth2Eq2PGVnOJ+FEfeFZASqu4OFpjcTALUo8EuhUiYlEAcZo0aRIbN25k2bJlgW7KKc17DIg9gLRPgBAf/8Xax4FYFZBresGiW829Y7x5V1UinJWGWweYt6e3drbFOQ7D0tm5vsi6NPdjG4+4B5D2bQ6RPceR/MAiUtp2ZNeuXbx46xns+0MTpl4cTkpKCodfPZvsJe9zIiPH1f1iZ21oFx7sroBUdxDqzzvN28xCz79bdZeJb8gMA057D8b8t/zxOCLiXwogUq9Eh8LFXeGCjmb3SoJtEGqnJr5fk2KvgIT6PsbOe0CnVTW5vi98cCm8eZF53+GAZrbr921h3m477n5s4xF3V471fGhyTz7+fimXXnopUTFmOiotLuLgwYMUbJ/L8Y9u4d5RKTz36D0U7l2JYVuv3doMLzwEopzvpTbGgNj33amNWTUNza509+/2ZftFJHA0C0bqFYcDXh3rvt/UFhbKCyD2Coj3NF1fylRAnK8JcsCIdp7PNY1yDxTt09ycymq3+rB76myf5u7HO7ZKZPr06Ww5BqPezyeq6ChTBqVxz6uzyV78DnlHt/PT/94A3iA0uRdRg68netAEQpqYfUb2Csi/15qrqd4xqGzbK8u+S29uMfhYrR4wF0wz8F1pasiWHnD/fqp2QYnUNwogUq/ZFyJLjvF9TIqPLpiKxHuNAakotNgHvXZvVvZ5ayZNkAN6N4dgh/m7NX6kRTQ4QiPIC21NTPvWxI0aSOy5v+OMkl9YNeNtNi/4kqJDG8iY8RgZMx4jvMMZhLUbxpaD/Unu3A+jpAfLDoSy7IBZEZlcziZ+J2MPIOVVQKYugzdXQOtY+Pa6k69a25As2+/+/VTsghKpjxRApF6zh4NWsb6PaVnFLpgyi5tV8JqISlwfoEOCed5/jDEDiPW6uHD3uiPWAEhHUBDRnc9lYMdzyRmdTu7az8lZ/h8Ktv1Cwc4FFOxcwIxfzGNDQsNIaNubwk4XMj/ociYN6YejGsnA/qXr6wv4cLa5eR7AxgKz28fXDKKGapmtAqIAIlI/KIBIveZwwJ2DYMuxst0jFo8KSCWmm5bXBeOLfeGz8qblAgx07jUzvqvn4w6HOeYkLQe22faROZprjh0Jikog5rRbiTntVopP7CF/82wK96+hWeZqju9cQ2ZmJke3r4TtK/nfD8+y/OWOXHHFFZw/4be8tL4lfzwLzmx78vecbluIzNf+Mtu99rjJKaz9ALInAz5aDzf1NytD/nTQNuBXAUSkfmhkPb3SGP3hTJh2ibkuiC/JVa2AeE/DrSiA2K4ZGeJ5375uyICW5Z/DOs4+ePVIDhzwGgwZ0qQtMafdStMrXuHeN+aRnp7Ojh07ePmtfxPZ51IcoRHs2LGDF154gbGn92LZ9x9y3RflD2gosnW72ANIno8v4N1ee9VkVXPtkYq8vRJeXw6fbKj9c1fEMDz30ylQABGpFxRApMGLC3f/a72qg1DDg80uk/LYw4nD4TkmZUCy7999tQ88v+T3ZfkOApawYHA4HHTo0IF7b7+BdndNp9WfjvLK+58yaNAgSnJPcOw/13P03cs4dOiQz3Nk20KERwDxUQGxzxIBswJS23Y7r3Eir/bPXZFi58BaiyogIvWDAog0CtY4kIgqTsM92aDVi7uZt9bKqvZ1SU5r5f69a3nTSnAPerUPBLXY97ppH+/+3d71E+SALk0hKDyazmdeyaJFi4gf9ywEh5K3/it69erF7373O77//ntyctyLXOSUF0B8fAF7B5C6qIBY01/r4twVKSip+L6IBIYCiDQKQ1LML+quTU9+rD2AnKzL5ow28M1vzB/wDCB9W8B742H61RVPW40LL/85e/dRjyR3NSbcq7vJel9bjkFoaCjxFzxO8kPLCW3Vn+PHj/Piiy8yduxYmjRpwsiRI/nrX//K4d2bXa8/cZIKiHcXTG2sPWJnGLAv03luPweQQq/AoQqISP2gQajSKPz5XHh4eNnl032JDTO/6EuNynXZWAuMgWcXTGxY5QaAegcQa1YMmJWbjc7ZMUlR5mya7SfK7vrbMwlIhQ22pcTDUvqS/OBS/i/lc2bPns2PP/7Inj17mDdvHvPmzQMeJaR5N6L6XMq+IZdiNB+KIyioTAXEMNwVkDZxsDfTs/vGm2FUfYru0Vz3e67o3HVBAUSkflIFRBoF+9oblTnW6hapzLohdvYKSEwFlQ077wByQSf37y1j4NEzzO6XyUPh/I7mnjc9vdYc6eVc5GzdYc/HHcGh/OY3v+Hdd99l165dbN26lalTpzJ69GgcwaEUp20m86e/svn54Rx4ug3HP5vM6kU/U1TkLnGk5ZjdMsEO6OG8rhUS/vgz3Pq1uUAZwO9/hHP+DVnO1V8/T4V7vzv5l7p99dFsP6/EqgAiUj8pgMgpyRqIWtUAYh/AGlOJ8SbgufBZXBiMsFVNWsbA3YNh7k3m1NRHz4A1d0KfFp7nsALJgWw4luv7Og6Hg86dO3PPPffw/fff0/mvR0m88WOiBvwGR3gsJRkHyP51Kq9PPo/ExEQuuugiXnrpJX5YuBqjtJRWce73l11oVoj+sw5+3AkrneNcP9kAO9PNnXtP5MGDP8DXW+D7bRX/DazuF6heF0xxKbywEH7dU/XXeo/5UAARqR/UBSOnJOuLtjJdMHb24yu7Toa9ApIUDcNsg1ftXTpgdm1E+zhvbLjZPbMz3bMbpjylBhSExBE98BqiB16DUVxA/pafyF37BUbqV2RlHGXmzJnMnDkTgKDoRIo6DSAzuSXpJSnM2tGStkd7YRSPwBESxhGvDdz2ZJrhxHLUFoq+2QLvrYbXxrh3L95nr4BUI4As3Q+vLYNvt8KciVV7rfe0WwUQkfpBAUROSdXtggmxDQ6NqmQFxCOAREFb22yX5CosyNW7uRlA1qed9FA2H/W87wgJJ7LnOCJ7juPqHm9zXdIaZs76mec++Im8bfMozTnGobU/cmitefw3P8E3r4AjMoHIXuP5vvRyTr9tNGAmpvVpsNW2rok9YPxnLaw8CN9tg9sGOp+3VUCqE0CsHWx3ppsBoiqfm7pgROonBRA5JbkqIJUMEZYwW6dlZQdixntVQBwO+N+VsPoQnNuh8tfu0cysLmw65vl4qeG5lsnPO+Hmr8s/T35JEAMGDKA0eQDvRD6EUVJE4Z7lXJi4leNpB/lp7UGSjQOc2DyPo2mHyV3+Aa8u/4B3H4/C6DyGqD6XsrjnhQRHu6cc2QOGteroDtvqqvu9AkhVB7Jas3gMzAXdejev8HAPCiAi9ZMCiJyS4qvZBdOxnB15K+JdAQGzG8beFVMZ1lojG726YPKK4Egu3DUT7h0K762q+DzWF7DVNeEIDiW8w3CuGz+cg9mwcg6c3QnuGVjC6OcXkrf2C4yNX5B9ZA+s/YK8tV9AUDDhnUZywbhLWBF/CXsTzXXyDcO9QZ99eXd7haTEMMdlVKWKYV/HZGsNA4jWARGpHxRA5JTU3BkE4iMqPs7byHbw2JllZ6lUxF4BaV6DPVC6OQOIfUl3MNfseHERpB6Fe749+XmsabiZBZ6Pt0twLxKWXQh5pcFEdDqLiE5n0fP2l7gleRW3/d+X5K37kqKD6yjY+jPf/ONn4H6Ote7Hk1su4ZzRF5NfPBCHw+EKIIbhWQEBcxZNVQKIfR2TrcfKP84XDUIVqZ8UQOSUdG1vc2bFVT2r9jqHA+4aVLXX+KqAVEfrOLNi472OR16Re5psZVib0XkHkDZx7vVAcgoh1zZWY1+Wg7ZnDyRh3EASxj1DStF2Rhd9xU/ffcWvv/5Kwb41PPvsGp599hmC41sR2Ws8eb0v5sjV5xAaHuFa2MxaA2XpAfj3Gvjd6TA45eRtti/fvuV4+cf5oi4YkfpJ03DllJQYBQ+c5p6lUZdivcaAVJe1JLu3nKKqDez0VQG5f6i5+Jk1syer0HO9jswC91oefZvDooc78dRjDzJ/3lz6vXiYptdN47wLLyciKpqSjP1kL3yTI2+Po11KM664/DKyF79HQvFh19ibj9fD4v3mbWXYKyBbalgB0WZ0IvWDKiAidSwkyFw1NavQ3fVTXd0SYa3XLJjcIs9BoENS4Ioe8OhPvs9hhRUrgNzQFx4cbv5uTQHOKSq7Xsdq51og3tOP26U040TwRH5/0UQOnMjn9+/MIW/DN+St/5q8jP38/N2XwJcc/xiiW/XC0e4sVvU9i+IWZ7E3s02l3rc9gOzJMKs+lR1AXOgMHHFhkFlYuxWQzIKKl9oXkfIpgDhNnTqVqVOnUlKiEWpS+x4aDpuPQbcqjB3xpYuPTe9yitzVibsHwU39zUXNmkeZ//q/22tcyIEsKCoxv4zB/GK2xDp/zy4sux/MsgPOY7y+cK21TE7kw7GiCCJ7jiWy51iMK6dyecJqdiz+mlnffkPh3hXk7N8A+zewYeGbAHzVrD13/Tia8ePHc+655xIZ6bUwilO6rQvGALadgD6VHIhqdcHEhdduAPkiFX77A/zhTLizit1yIqIuGJdJkyaxceNGli1bFuimSCN0c394/jzP6bLV0c1HANmbYQYNB2YlIznGHKtyXkdon1D2+OJSc78XqwJi/xd8tLOqkFNYtlsn9YjnMRZrefoT+e4ZME0izJVZC5IGMOjaKSQ/tJw/fJ3Gmb/7gtiRDxDWZhA4gig4uou33nqLiy66iMTERMaPH8/bb7/N/v37Pa5hVUBaOLuwqjIQtcAWQADya+nfGL/9wbz9y6+1cz6RU40qICINSFcfAcQalNkiBsK8dtEtb7XWHSd8B5C4cPdGfdY6Hikx5hLwRjnntAJIeh4cdi4YNrw1fLvNPIcVHvp0SCKNy9jT6jIASvMzKdg+n9ElM5k7ewZ79+5lxowZzJgxA4ABAwZw0UUXMXrseLILBuEICmJYK3Pp9/LGgRgGPDXX3NfmyZHmY4XeAaQGFZBjufDNVrism/vvdDJ7M83g5P3ZiJzqVAERaUBaxri7SSxWNaBVbNnjvasVnZ2DWHekuzeUsweQ8BB3lWXRPvPWe5aKdwBJsHXBWONG+iebt9tPuMeO9E/2fG1QRByRvS7k9idfZ/fu3cxfuoZnn/0Tw4cPx+FwsGrVKp599lnOPH0oB55uw4lP7yZs5/cUHd3O8g3b2b7d/MnLc/fP7EqHaWvg3dXuCo6vAGJUIjj48u4qmPKLuQx9cCWqWUv2w5nvw29nVe96Io2ZAohIA+JwlB0HYm0U1y6+7PHe+8p0d762vAoIuMPDEef+Lr2am9NnLeVVQE7kQ66zutClqfkv/qJSc9ZNVKj5mK99bvZmwq97HFy/sC+x5/+RhQsXcvjwYf71r39x5ZVXEhUdQ0nGAbIWvMlLk8Zy8E+d+fyuznTubP40b96cG2+8kVmzZrF4j7u8Yb0/K4BY67GUGmY3VHVYS8Kn5VSuO+2lRebtjK3Vu55IY6YAItLAeI8DyS82vwxv6lf22PBgz3+pW104OysIIAOSPe/Hh3t2/ZTbBZNvzk6xjrGPP+nTHIKDPBdls+zJgNWHzS6e+c7dbmObJHGo8408/uqnzFx9hKQ7viXlnDtp3boNjvAYHOExRMfEEBkZSXZ2Nh988AFjxozhtrNbcfyzyeRvncPxHDOMWNNu7e+zut0w1tTk7EJzdtPJ7Eyv3nUagpJS+OPP5nouItWhACLSwFzdE/q3gIEt3Y/d3A/6JZc91nt3XSu8bK9CAIkONfehsZTpgrFXQJxf0JGh0NW2Zkm/FuZtUx+TXPZmuhcas8advL0Spi6Diz+BHMOcWXPaXW+yd+8eRr6VRZu/ZjFjXRY5OTn88f1fGT/hHpo1a0ZuehrZv04lbeq5DO/Rkkuvu53187+hNC+DmDBzoC5UP4BYXUxZhZXrgjmcc/JjGqrpm8yuqCd+CXRLpKHSIFSRBmZgS/jqN/DqUnPX2dax5jTf8sSEusOGFUCs7hUoG0A6N3WvWwJmgOmZZDufdwXEGgOS5642RIWaq5wGOczxJtf0ch7rY+n7PRnuLp5jeeZ5lh9wP2/tA2Ndp28L85xrDkP7BAcfZJxB3JlnsG7qy/T9/Y/krv6UvPVfkZ1+lK8++ifwT3AE8UqPQWSmnE1Ix3M4mn4mSdE+Bs2chL0CEnSSf7419hVX5+0JdAukoVMAEWmgLu9uVgxu6e97bIUlyvZc0yhzOXh7APEe1BrkMCsWv+4175+sAmLvgrHGdkaFQMtYeHWs57EJ5QSQRFtlxL6JHbirItZr+7WALzfD2sPudmUWwLLDoe41SEqKKdg+l9w1n1O8dTb5advYvXEZbFwGvEDf90M579xzueSSSxg/fjytW7cu2zAfrApIdiUqIJuPun8PbYS1ZmtwMZTdkVmkMhRARBqoVnHw99EnPy7GNhMmNMjc0dcKIOHB5swXbwNa2gJIGLS1LVkfU846IEW2gZ1R5axS6qsLJqPADCGWHSfc64kArDjoeR1rAbLUo2YlxPLDdvfvjuAQIrqeR0TX8wAoPrGXi8Lm8sOPc9i7dg7Fx3Yya9YsZs2axT333MOgQYO4+OKLGT9+PP3798fh8P1tmm0PICcJFVtte9YUlZqLv4U2kqm42YWw2/aZ5ReX/5mLlKcR5nIRsbNXR0KDoEOC+36LGN+vGdDC/XtMqLlrcF/nbJi2XrNtIkM9Z8lA+Tvd2rtgokPdlQ97kNhy3L0pHsB659LzVnhJcfacHMl1V0cAZu8wb70rOgAhTdpwzsXXM+vTd+n41A5aPraJq+7/K6effjoOh4MVK1YwZcoUBg4cSNu2bbn77ruZOXOmxxRfcAeQyowBsVanteQ2oi6ZHV5Vqtwi38eJVEQBRKSRs3eZhDgrIJYxnXy/pr9tIKr1+o+vgPk3u8di2NkfC3aUv+hWgu24kKCyYQZg/m7PDeSsyorVBZPo3E+nsATW2LoBrE32RrTzfe2wEHM2zx/OgtAW3Vjd+fd8OHMBBw8e5N133+XSSy8lKiqKffv28eabb7pWZ73ooot488032bVrt2t5eu8uGF/ritj35wH3DKHa9O4q+M3nVduMsDZ4b+inACLVoQAi0shZpfGwYHNWTGtbd8ql3X2/JjEKHjwNbh3g3sE3Osy9FLo3e2UjKtS8ji/2fWeKSqGNj92IN5Wzyql1jYgQd5XD+9jYMOiVhE9WlWZiXzizjRly/rYIWrRowS233ML06dM5evQoM2fO5K677qJNmzbk5eUxc+ZM7r77bjp0aM/ev/TixFcPc3zDT5QWubcTLvKxroh3AKmLL+m3VpgLxtkH7fqD9w7DjX3ArdQNjQERaeSs1VCtdSuGpphVjR7NoGcFm+PdP6zy17APLq1ol1p7MCkqgTY+KiCWuHD37B3wrLI0i3LP0rFLifW91gi4qzIOBzx2Jlz4kbms+0PD3WuWREZGMm7cOMaNG4dhGKxfv54ZM2Ywc+ZMFi1aRNGhjRQd2kjWnL9xNDyasM7nENl9NOtHjWZAz84eY0fKdME4A8iMLeaibDXdmDCjwD3NN6Og4mNrW6FXAFEFRKpDFRCRRs7qQrFmYiRFw8Jb4INLy69UVJVHBaSS/6wpKvWcXRMf7rl0/BU9yr9Goo9uIDCXqveeVmyxj1Pp3dwc0wLl7yvjcDjo06cPjz32GL/++iurth8lceInRA+ZSFBsC0oLcsjfMIMTn9/LoN5dadWqFVdddRV///vfWbR4CQfSCzEMg+DCDIqObGP50qV8u+Yok76DCz50/g1K4JrP4PE55n3DgH+tMXfaPZlttkGuGfknP97bsVx4bSkczj75sd4UQKQ2qAIi0sjZu2As5VUJqqtJJSsg3gbaxppEhppThNc5B52e3xH+twHXuAv7NZpF+T5fSmz5AcR7XEpyDKxNcy+vfjLB0U2IHnA10QOuxjAMig6sJT/1e/I2z6J0168cPHiQzz77jM8++8z5gjAwSqHU7J+4GTPUhLYZQkSPMSwaOgZH66Es3h/M4v3w5Ah4foE5rgPggk7lbyYIngEkvRoVkA/Xm11QR3Lh6bOr9lrvLpg8dcFINSiAiDRy3hWQumAfXFqVAJJiWwvsUDZ0tg2Q7dvcHDBrBZKEcgKIA/f6I94BpHUs7HN2hXgHkObO8SxWACkpNRdCa17OOJccW5ePw+EgrFU/wlr1I27UI3x1eR5Zu5azYMECFi5cyLxfF5Jxwl1acYRF0yQhjuNpByncs5TCPUs5fdYzxCU0pbjjaCJ7jmP6ijG8u8pdEtqbAT3KGc8CntN8q1MBsSofm8upAFXEuwJSFwNspfFTABFp5FxjQOpwDYrqdMFA2S4g+2JWseHQyRlAYsM819BIsgWQLonubhTvAHJaa/jM2Z1RXgCxxlHcNRN+2AGfX1V2B2CoeKaJERrJWWedxVlnnQXAV5sM7vnvLga0CiUmPpFFhyP5+wVw4MABprw7i/zU7wnd9QMZ6cdh5UfkrvyI33zoIKztUCK6jyay+2h2Hh9Kj6Ty/5geXTDVqIBY42u8F36rjDIBRBUQqQaNARFp5PxRAfGeBVORy7p73k4abN5e3NUcHBoRAo+cbj7WybmfjPfU30RbABlk2xPHewzI0Fbu370XXPOugPzgXEfE6gLxVlEA8Z4Fsj/LQUhiB7q0b01cjNn43CIIb5JCzLCbaXbTJyzcdIS/fDifuFGPEZrSDwyDwt1LyJz1DIf/cQZXDUniyiuv5K233mL79u1lrmmvgGRWI4BYoSUtp+qv1xgQqQ2qgIg0clYA8bXiaW2xB5DyFiGz/OVcc/0Ra72O355mrrw6rJUZHjZPch/bxRlAkrzGfDTzCiAfrTd/954FM9y2wrr3YmmuAJLr+XiJsz9nTwb8uAOu7W12K+VU8CVrdUGk55vjKlY61ydpFeeejptb7NmNk1EUQuveZ5Jw0ZkkXPQXitP349g2iyb7Z7FxyWxys07w+eef8/nnnwPQoUMHRo0axXnnncdpZ53Lvkx3/0x6Nbpg7K/ZfqLsJoQVKTMGRAFEqkEBRKSRO601XNTFHNRZV+xjQE5WAYkKhTGd3fdDg8tv23kdYNIQOMdrcTErgIQEmZvnWZJjzKD16ZXm/iRt482AcjCr7NgOVxeM1yyQUmcAufYLMzzsyzIHiFZUAbG6IF5ZCv9e6368VSwcdwacvCLPqcPH8yDLVnkISWjFdTfdQr8Wt/D72SX0KlzG6YWzmT17NosWLWLnzp288847vPPOOwCEpvQlvPPZhLcdwv78QZSUdCU4uPL9bPZxI9uPVzGAeFV81AUj1aEAItLIRYTA1HF1e42qdMFURVgw/P70so93SzSrIv2TzcGqp7U2B5xa1Rd718tnV5nTXb0rQNaiasfyzAGoFut3q3LxzRYzgORUogvGvqcNmG2yxmrkFnmGmBN5Zdcyubw7FBvgCAomL/k0nph4Gk888QRZWVnMnTuXn376iZ9//pm1a9dSdMD8yQYWAgl/imHAgAEMGTLENR4lMTGx3Dbbx41UdRyIumCkNiiAiEiNVXcabnXFhZtrmYQGmQNZP7mi/GODHL67nxIjzedKDThq2/KlxGtZdWt8RHYFX7JWAPFeKbZ1nDuQ5RR5hphjeZ5jL4akmINfDzhn7ezLNMNQcBDExsZy0UUXcdFFFwHw5Iw0Xv90Ds2OLWTXxhUU7l9FdnY28+fPZ/78+bz00ksA9OnThxEjRrgCSUqKObq21KjdAKIKiFSHAoiI1FhcuHs6bFVmwdREefvNVFZwkNmVk5YDabZumBKvZdWtcLHKtivvCa8xF9YYCO+xES1j3QHEuwvmRL77/h/Pglv7m2EqOcb8WxaVmt00ST6mBR+iOdEDr+GuYdfw9yVglBTz1XmbWLt6BYsWLWLevHmkpqaybt061q1bx9SpUwHo2LEjZ555JkOGj6AgbSQhzTrhcDg8ZtRUhhVAQoKguFRjQKR6FEBEpMaCg8wdc9Pz/VMBqS0tos0AYt9avsQoG0JWHITlB82Ky3V9YOoyz+etCoD3bJKIEPffw7sLxj4GJD7c/BuCeZvgDDnlBZCtzmnHA5wzgBzBIbTu3JsB/XozceJEANLS0pg3bx7z5s1j/vz5rFmzhh07drBjxw7+/e9/m9eKa0lYhzM4Ed2UuxeHEBYaQlhYGF27dmXgwIH07t2b8PCyK7tZASQh3Kwe1aQLJrfIHIfToQn8c6U5hubjKzzXiLGk58NPO2FUx8ovpldqeE7vPpll+82KWd8WJz9WakYBRERqRRNnAKnNMSB1LSXWXGfE3gVRUlq2wjH5W/N2fFdzbRJvVpXE12wUqyLkawyI9cUd67XiadNIsw3H8iijqAT2OMendG3q3jPnWJ4ZDFo5N/hLSmrO+RddyZVXXglARkaGqzoy6+f5rFy+lJLMg+StMVdufXNh2WuFhITQo1dv8poPYdRZp3HflcPp1q0bBSVmWoqPMANITbpgJn9nhoqfboBn55uP/XUB/GNM2WPfWA5vrjCD3dyJZrWoIrvS4dJPYGI/c7bVyWQWwITpZgBZc2fVgotUnQKIiNSKJpGwMx0iG9D/q7R0foHZA0husVl5sDuQbX7ZPTgcNh4pex7rC9g+s+RB5xeeqwum2DOAHMszuy+g7PLxiZFmm7zbAWb4KC41/87JMWYlILMA7pwBuzJgxrXQpzm8tNiclfPxFeZ05Pj4eMaMGcOYMWMYtweu/SSP5ulLydu9nAPHc7moUzHt4orJzc1lw4YNrFixguPHj7NuzWpgNdtmv8ObT5rniWk3kIyEPiT26EtBVB+yEnsB5SwhexJW94/9Mygv0FjH5hebU69PFiqW7DeD3HfbKhdA9mWa3WgFJeY1GlKYboga0P9V1K2pU6cydepUSkpKTn6wiJRxfR8IccAZbQLdksqzAsgO25dfdkHZL/7WcfDR5dAmruxMF3APLrUGdn5xtXuBNGsJ+b0ZngFkZ7p71o6vCgj4roBYbe3QxBwzEh8BezPN8AGwPs0MIKuca5HM220GkB0n4D/r4M5BZjuDwiJp328krc8ayZeb4VgzePtq95euYRjs3buXW95YztKlS2DfYor3LiMjI4OMtXOAOaya53y/Dgc9/tyNYcOGuX769OlDaOjJv8Gtv4m9+6rU8H2sfeCsd5XKl6POKdD7Ms2N/k62+eJB21ig3CIFkLqmAOI0adIkJk2aRGZmJvHxFewRLiI+XdGj7A629V1L5zgD+7++swvdX/xxYXBNb7ilv3tMgndYAPcYEqsLxr5w2uAUczn8A7Yvt5gw8zquLhivCoi1zokVhHacMI/v28LdVqsryHssxJFcz7akHjVvr/vC/ILdlwnntHe+NgK6NwM2w8aj8OJCeHKk+ZzD4SCldVsOtW1Lk+TLiQqFtbcXsW7dOu59fw3r1q2jSeY69m1bR2nWYTZt2sSmTZv417/+BUBERIRrWrD106VLF4KCPJfktQKIfU0U7zE4lqO2ReNyK5gW7X18TpH59/BeUdfbIdtnpJk9dU8BREROWSnOCoh9EGV2kfuLf3gbePwsz9f42qF2+wlzcS7rS8seCiJCzEGTX212P3b3IHhhkft+eRWQo7nmImoXf2ye+6cb3BWQjgnmrX2TPoAjzqXlrQCyyRlArH/dL9rr3oU4IcIcVPvuKjO4WBv3WdYcds/UyS2CUkcoAwcOpO3OgezrbAaz91ZDcyONp7suZ/HixSxZsoSlS5eSnp7OokWLWLTI/UZjY2MZOHAggwcPZtCgQfTuO5D8oi44goI8KiDeU6Et9gBS0bRoX8fvyzx5ALFXQPw9s6ekFBbtg15JJ29nY6EAIiKnrJY+ZlrkF7v3h2nq44vAHkBSYszKRloO7Hd+eTsoW9EY39UdQBzADf1g6vLyKyDWdY/nwVNz3SHg81TYaQWQk1RArPEoB7PNAa+WqDB3OIkPN38ePwvun1V2tddf93jeTy+AFiG2WTDO8JMf0ZwxY8cxbpy54l1paSnbtm1j2bJlrp9Vq1a5FlSbO3eu65yO8BjCWg3gkwEDyQ4fQFir/hSn9AQ8+z/yiz2nMVdm5s0RWwDZmwl9TjKz5ZAtgPl7cbUvN8ODP5i/v38xnNvBv9cPBAUQETlltYh2r19iZ3Wp+Aog9mpF0yjzX+uHc2Clc52QuPCysydGtDW7czILzdfHh8Nl3eDD9eYeNd775yTaxoAsP+B+/ItU8xzg3qivTADJMQepZtq+rH/c6f49xOEeS2G91npPVgCxxkvM9wogf5oH1/d1r3fSuanzfRWYYcXa3ycoKIiuXbvStWtXJkyYAEBxcTGpqamsWLGC5cuXs2LFClavWUN+XjYFO+azeMd813U+CQlj03O96NGjBz169KB79+40bdMDo7gzjpBwj7ZWxD6Gxru648vBAHbB2Lt/PtmgACIi0qiFBpt7whzO8Xzc6uZI9BFAIkIg2GEGj7BgcyzG4RxzrRAwx1V4Cw+BCzrBZ6nuCsrEfvC/je5Khp0VfPZkuLsjQoPcX6JxYdCjme/rpeWWXY/k682ez7sqIM7XxjiDSHYhpB6B33xhdq9YA1mjnZvxfb0FNh0zQxuYAebyHjBtjTnA1QogvoSEhNCnTx/69OnDTTfdBMCag8WM+cdmivatpGXWSrZuWEXh/tWU5mewatUqVq3ysTVxUAiOkDAOhITR6rdRtG/fnm7dutGtWze6du1K37596dixIw6Ho0wXzMl4D0KtKsMw/06+uulOxr66bEZB+cc1JgogInJKaxlTNoCsSzNveyWVPd7hML9gMgogLMisRCzc5w4gCeUskHVZdzOAWOt0dGtmTpn1taCWFXysL8TwYLikmxlYAE5vY65CCr7HgHjPEJlnq2QUlrgHsloBxKqAZBbAnF1mQHlpsflY23izPVYY2XnC3XUVFgwT+pgBZPYOc7yKr26t8uSXhhDWshdhLXvRo9UNZO43Z9/0DNnF3W3WkpqayqZNm0hNTWX9xlRys7OgtBijsJjiwlwO5KZz4MABFi70XMQkLi6Ofv37s50BhLYeSFjrAexp24OKvvIMo+ZjQJ78Bf67Hr691vx8q8K+wZ93gGysFEBE5JTWMhZWHy77+Mh25iZ3vsRaASTYPRtls3N1Ul8VEIAz25p9+/aKR/dyvqSaRnnejw2DK3u6A4i90uC9hkheMRw4yb/2rfU0rPATY+uC2ZnueWzvJPdCa2AuEb/fef6wYOiaCKe1gsX7zbU5Hhxe8bXtsm1ftFa1wuFwENm8A5dc0oFLLrnE9fxH6wx+981xWoTncyijkPiQAv49Lpvt27ezefNmNm/eTGpqKhs2bCAzM5P58+YB81yv/yA0nI39+9KnTx969OhBz5496dmzJ23btiUoKIisQs+qR3UqICsOmt1f8/dUPYDYKyAKICIipwBrJoxdsKPs7Bc76ws7LBi6NPV8zte4EUtl+/WbeoWYuHBzs7oezcxumXPbu5/zVUHZ6gwYsWFld9wFd7dOglcFJK8YtnltTNcqDo7lej5mvT7cuR/PDX2dAWSDOZ4mLhxuH1jROzTZ22YfMFrqYxrusTwHwdGJdGkNR/dBcTAMHgyDBw/2OG7HsSLueC+VZpmr+HbeKgr3W906ma4BsXYRERF06dKFlA7dSM/rSkizzoQ07cDerh0o6d6a4ODKbzpkdZ1YYbQqCtQFIyJyavHVZXBtb/Nf9uWxAkhocNml2XtU8V++voQGu5dYB/fA1k+uhPwiaGELTb4qLlYA6d3cnNppGdvZXBXU9VpneIm2jVlI9VrptVWs70AAEOb8Brmgk9nGtBxz9VUwQ4n34Fpv9oGk9n/1e++2C+4di9vFm++poMS9kuyyAzAg2bzes7+GsjWsL1ub9aXJ5RNpHw87T5RSfGwHf+6xij3bNrJxo/mzZcsW8vPzXZv22T08FR4NCaFt27Z07tyZ7t2707NnT9eg2KSkJBxeK5tlOru+ahpAsgqqvodNQ6QAIiKnNPumZ2e2gZ5JcO/Qil9jr4Akx7gHaYLvcSPVkRjpGUDAPW3WznsMCMAW5xdgM6+unHZeayxa5woLNqsZBSVlZ3+0ii2/S8DakTgsGEZ1gC82uZ/LKKhaALHzNQPFqsK0T3A/llsEH6yF/1toTnV+bWzZ2S6t4iCnKIgjQZ0ZPKozN09wP1dcXMzu3bvZvHkzH8/dwvRfN1N8bAfFx3dinNhFcXGRawO/H374weO8cXFxdO7cmS5dutC5c2c6de7Ckc1dCEnqwuagRA4cTOPA/n3s27ePjIwMevToQZ8+fYiM9F0is4cuA7M6VNkN9xoqBRAROaXZNzQ7ow3cM+Tkr7HW7QgLMgelJse4B3bWVgBpGukej+G9TohdRV0w8eFwUz9zkOgzZ/t4rS28xIZBgY+l31vFuQONtzBb78SYzl4BJN+8fqlR/pLmmeUEEF/jL6wumpYx5oygolJzCfx3VpqPf7PFDCDeq6g2izLPdyS37FogISEhdOrUiU6dOrGl6Tjmprifu61fCTd1OsDOnTvZsmULqamprp/du3eTmZnJypUrWblyZdnGOoJodV/ZslFQUBDdu3enX79+JCcnk5iYSLNmzUhMTGT7pgQKTsQTFBFPUGQCRzLjiU+qfAIxDLNfzLsqk1MIxUb9DDMKICJySrOPAYms5N4f9goIeJbPE6PKHl8d9inA3gNNfbXFzhpDkBABk4eYM2gGJJu7zlqiQj0DREyYu5vDrnVs+ZWKcNvrR7aDns3MJd2tNpz5vnm77i7f1ZByKyA+Aog1SLVZlNn2jAKz6hQb7jnrp8hHADEMcxZPRWuBWDNgrHCTXxpMmzZtaNOmDSNGjPBsX14eO3fuZOvWrWzbto2tW7eyLnUrS9ZupSR9LxilOBwOWrZsSevWrYmOjmb9+vUcOXLE1f1zMl2eMANSTEwM0dHRrtuoqCgiIyOJjIwkJyeHI0eOcOTIEY4ePUpQUBBNmzalSdNEmjZtSkJ8HD/vDYeQcK7qE0HnTh246aabaN26nNHVfqYAIiKntObR7nU9Krv5mH0MCJhLm+/LNM9TW5pWMoBUNE4gIcIMVQOdG+PZu5u8/0UcU8414sLN6sYbKzy7msAzgESEwHcT4KKPzGnMaTnuqsWudHPGz9bj5jTh050bFpYXQHJ9dMFYASQpyj0NOqfQ829TapStgCRFudtZ0VogVgBpl2DOEvLVDbT2sPm+RnWMdM2isaw7DBd9DKWFeZTmHud35zfngdPd/0EZhsGBAwdYvXo1GzZs4OjRoxw7dsz1s35PBlmZ6ZTmZ2Dkmw0tLi4mPT2d9PT08hvu/T4OHuTgwYNlHv/XCvP2qaee4uKLL2bSpEmce+65ZSom/qQAIiKntOAgc0XUA9nmFveVMaoD/LAdznPOavnTOeYX4Q19a69dHhWQSi5sFRLkHpgJ0MRrfEirCgKIr032wOxi6p8MP0yA5FgY8o674hPmY4KIdd4029oq1viGUR+Ytz/faA7eLS+AFJdCUYk74BWVuKscVgUEzDAUbQuNh7M9AxKYf0crpFQUQKyVSDsmmAHEVzfQXTPNJffn32Suj/LVZnNA7LNnu6tOQWGRBIW1YpvXrskOh4NWrVrRqlUrLrzwQkpKzf/2LFd+ag6mBTBKS/jbyCyGN88mJyeHnJwcsrOzyc3Ndf3k5OQQHR1NUlKS66e0tJSt+44z4cNjlOQc49Eh2fxlbgFGUT43985n5a8/MHfuXKZPn8706dPp1q0bd999NxMnTiQhIaH8P04dUQARkVNel0QzgFR2Ea3TWsO8m9z34yPgz+fWbpvsFZCKxoDYnd/Rc5ZLuwTP5+PC3Tvxeg9etQeQCzrCDzvMbhuLta5FuwRzTEiww/ML1GKNK7EvLZ5d6FmZSD1iBpCsCqab5hZDfLC5MNpTv5iPBTnMdlsVqJwiz6m820+4V3m1NItyV4n2V6IC0sE5q8lXN5BV0VmfZgaQ+7437w9JcXcxWUv7lzcTJqPAXNL+q83wyhizugSeg1AdQcGUhifQunVC+Q0uR2lcOyK6mb+fewW86jzv7ddBjz/9gQ0bNvDGG2/w73//m82bN/PAAw/QokULfvOb31T5WjXl4z8fEZFTywujYNolMLhloFviZl+MrKIuGIBZE+Dps+EezyUx6JDged/hcHfDeE/ftY8luW8ofHIF/OvSsteyzumr+gHuCog9gKTn+x6nUdF+LlYAuOkr2OWsJiRGmqHHVQEpdG+6B+7VaO2Sotzv+VBO2eet81gzfaxdhr27YIpL3SFhyzHPQHXEtvx9D+cg5B0nylZRth6H8z8wF5QrKPGcIm2du5kzeFZ3LRB7Bci+tkq+8/y9evXitddeY//+/bzxxhucd955XH755dW7WA0pgIjIKa9FDJzT3vyCri8qOwgVzPEVN/XzXB8kOtT3XjbWoFvvc9oDSIcmZpXH18wJaxrsyQKIfXn7jALPxcxO5MGy/bDBueZIe6/pweC7AmFNK7ZXQOxf1Ev3+36NNdMpPd/3eQ9ku8/bPNr83Ts82O9vPobHPjMO3EGoe6K7K6zH6+a4Ecu01ebfxRorZG+7tRR7kvP61V0N1f7+7N1g+V6BKjY2lrvuuosff/yRsLBqbF5TCxRARETqocoOQrWzB474cN+ByhoHUl4XjDXIszxWBSS8nA58q7Jy2FYBySjwnGFzJBf+OMcc+HtJNxjmY1KGr4GoVgCxKiAZ+Z5VlF/3ln1NYpT53qyxIvbKjMXqmmkV654JlVdsTu39PNV53yuA2PeNOZHnDgzxEZ5dV6sP2Y6zQoqzO8veXeSqgDjfY3UDSE4lA0h9oAAiIlIPeYeJygix/T96dDkh4to+ZrXniu6ej1uhw77Qly/WXjbR5cwYcnXB2L78MvM9KyBL95tf4iFB5gBOXwHLqjjYn3MudeG6tj0EXNDRd1vCgt1rtXi/xrLfOT23VSxEOYNVZgE8+AM89IMZMOwVkF3p5o/laK67mhEfDg/Z9sOxj1Gxxry0dm5I6FEBcQaQJGcA8R7LUlm5DSiAaBCqiEg9VJ0KiF15VYw+zc3xLt6sf5UPTSn7nN2QFLhrkOe/8u2sCoj9izCjAI7ZKiDLnWM1hrUyj/f1/vKKzMBh3yXW6tax/jbLnbNGYsPgnfGw6ag5uHNPBszY6rkSbEvnYnEVVkDi3BUQ+5f3vkzPAbclhme15Uiue6BwfDgMbw239od3V3tWaKww4gogtpBhBRBrb6HF+8zZPyFBsGCv+fl4r2zri/3vfrieBxBVQERE6qGIEPNL7LLu5jThyurs/AK7okfVrnduB1h8Czx8esXHBTngsTPdsze8+arWpOd7BhDLKOc0Zp8BpNj80rQv8mZt5mdd21r0zAo93ZvBI2eYwQbKBhDwXQGxFihrHet7LZh9WWXHhPyyy/370Tx3mLDaYgUSe1eKFUDaOAPIsTxzgbTCEncXzJjO5kDUwznmTKRvt8GE6XDF/8q2y5eG1AWjCoiISD315Miqv+a/l8OKAzC6U9VfW9lpyBXxFUC8B6FazqsggHjPnHnmbLjSGap6JZk/1iBW72ue1dbc92Z8V/djyc73diAL3l1l7vkz3Dn2xKMC4uNb8UAWxHgFE/sMk6O57oGl1nuxKlDZPrpgrACSng+XfmIGTavSEx0G1/SGqcvMfW6s8+zyWlekPJUdhFofKICIiDQiLaJhXJfAXd/X7rwZ+WUrC52butcp8bXQ2s4T5m6+YI6LmNjP8/mre8GUX5zX9AogHZp4rtMC7grIrO3u8GAtiGYfA+JrzZX9We5uE1+O5UJEsGdbrOCQVWiOeXlnpbtLxPtc7652/x4RDBN6wxvLzWm6SZXodrGzV0DsVaeCehhA1AUjIiK1prIVEKv7BTwrINaCXjvS3QMxfe34e2k391RgX897swah2isXt3wFS/Z7BoOw4LIDbPdnuisLvva0KSp1T+W13r/1nrIL4a0VZneKpXl0+dOYw4LNSsz5Hcu2tzLsXUWlhvv3+lgBUQAREZFaExturoth5z0IFeACWxeRPYD0cA6Gta9q6itgJES4u5ma+ljvxJtVAbHblQFXf2Z+UYcHu8eMeF/vQJZ7YbLett2O28a7py9bYzisCpC9AuK9KmpMWPkzm6xg4msMj3211PL4WkIeFEBERKSRC3KU7cZIz3dPW315NLw6BgbZVp21B5CezgCyO9292Jf3njaW359uriNyYyX24PEOIJd3d48pCQmCe4e6l2z3FUCsL/aUWPdqpQ+dVraLxAoWVjA5nA17bUvAhwebIcPX3jshQe7ZNvagY8moxNTccgNIJcKLv2kMiIiI1Kr48LILaRmYYxsu6172ePuXcbsEs5sjv9jcVRfK72JpG2/up1IZCRHml799uus9Q8wVZOMjzHNZvAPP0Tw47qzgRIbCtEthbwaM7QwfrjO7iwBCg9xdNFYFxLvyY4WtAh+BwN4tkxLr3rfHklHgXim1PKqAiIjIKct7IGp8uFn1+Mt5vo+PDnNXHyJD3KutrnSuF1KZMR4n43B4VkGsJdf7tPAMHwBNfHTp7Djhbl+f5uZAX4fDc6qvffXZ8nYXjrV1zXizBxCHw11psVRmfxgFEBEROWXZxzf8bjgsvx0u7lb+8UEO9xdzeIh7tdXtzi/98rpgqirZNs24eQWVBF+BZ5uzLd6zeRLtAcT2uvJ2MLYe97UTcLjXwFTvdlSmCyZHAURERE5V9gASF17+jA8764s5LNgdQCwVhYWqSLFVQCqa3uor8Gw7bt5GegUQ+3nsY1miQssOxgV3pcfXSrXefyfvPXKO5cFffnUvgmYY5nTd2c4ZNvsyYXc564X42oQv0BRARESkVtkrAb6mrfpifXmH+wgg1jLxNeWrC8YXewCxpuRaU1qjvN6PdxeMxV7VsbPW43jzQnPa79nt3M95B5AHhsENfd37Ak1bY07pnfiVeX/ZAXh+Adz2jTlG5ex/uceqeKuPg1AVQEREpFbZv4i9KwblGdnWDCG9m0OnBPfjwQ738vI1Za0FEhLke5yHJcH2XNdEz+e8u2CalVMBAd9VDqsr5My2sOBmuN42g8d7h+GoUPjTOe4py6lHPJ8/kOX+fe5ucz2S8tgXIjuYBRuPlH+svyiAiIhIrfIIIJWsgDx6Jqy+wxwQaq+ANI+ufBXlZKyl5pOi3F0hvtgrIN7Vl4gKAoj34NsY59+hjW3l0zyvsRitbeNSvMeAuM7rPE+JbWExw/AccPrDdq92eQUs+xiQm76Csf+F1Yd8X89fFECcpk6dSs+ePRkyZEigmyIi0qBVpwsG3Gtg2AdwlvelXB0Dk81umLHlbKRnqSiAeHfBJJXTBQPuLhj7OYq9qhStbOGkvPfqa1BsTpHnbrc/7/J83ntfHyuAlBqwybkw2j9X+b6evyiAOE2aNImNGzeybNmyQDdFRKRBs38R17R60a2Wxn+AOWNl0S0w5SSb/Nm/8LtXoQumTAXEGUC6JsKfzzHHeLx0gecxceHurpvyBuv6WjX1RL5nAPGe5eK98Jr1fLptJs2CvVBSQbdNXVMAERGRWlUbAeSf4+H01jBlRO20yeKooOvFYm9/hybmmBGL95iWqFB3KPEOCkNSzDEs57Qzx3psuBtGtKMMa3O6cgOIjwpIej4cyi7/PXgPsrUCiH2H3ON5ZggJFK2EKiIitcr+hVnZQajezu/o3pDN35pEwnW9zTEXLaLhvA7mLrpQtgICZhVkT0bZQaj3DoXbBrj/BuUFjDZx5qBQ70GoFp8b/OWby7zbjWwHtw8wQ98vuz2f8xVAHhpedpCtPymAiIhIrarOINT65jnbqq2TBtsCiI/3c0Ybc9+aPs3LPleZAGYNRK1KF0y6VxcMwIBkOMtZYVl12PO5/GJz4KoVQEa0hfuGnrxtdUldMCIiUquqOwi1vuqXbK7J8Zte0D6h7PPPnQur7nB3pVTVQOfGfJ2a+H7eVxdMWk7ZfWYG2jb48w4tBuZuulYAOdmeMv7QCP7TEBGR+iQuHLolQlFJ+dvONzS/Pa385xyOmgWtC7uYIad1rO/nff0Ntxwv+1j/5Ipfk18CR5w7DDevYCVYf1EAERGRWhXkgJnXmv/qDlad/aQcDs+1QrzFhpvLutuWAXF1CbWPdwa+Zp6hw1fVJKvAXQGpreXta0IBREREal1oLa7fcaoLcpghJNO2gZ215PrNA+CmfmVfYw8jUaHmomUbj9SvLhhlUxERkXrO12JkCRFwdU/fx9sDyJAU83ZtWv2qgCiAiIiI1HO+xnTc2Nf3tGDw7IIZ7Awgaw7BIWcAaaEAIiIiIifjHUDCg2Gij64XS0wYXN4dxnU2p9wCLNlvTscNdkCrcga8+pPGgIiIiNRz9orGuM7mDrnNTjKT5e+jzduCYggNgoIS837ruPoxRkcBREREpJ6zV0BeuqBqK8yGh5izZNanmffbxddu26pLXTAiIiL1nBVAgqq55khf2yqt7RJqpUk1pgAiIiJSz1ldMNGhldtQz1vfFu7fVQERERGRSrEqINFh1Xu9PYD4Wk4+EBRARERE6jl7BaQ6ujZ1bwzYsZw9Z/xNg1BFRETquS5NzdvyNqw7mdBgeHUsHMyq/jlqmwKIiIhIPdc1EeZOrNkCYud3rL321AYFEBERkQagvozdqC0aAyIiIiJ+pwAiIiIifqcAIiIiIn6nACIiIiJ+pwAiIiIifqcAIiIiIn6nACIiIiJ+pwAiIiIifqcAIiIiIn6nACIiIiJ+pwAiIiIifqcAIiIiIn6nACIiIiJ+pwAiIiIifhcS6AbUN4ZhAJCZmRngloiIiDQs1nen9V1aEQUQL1lZWQC0adMmwC0RERFpmLKysoiPj6/wGIdRmZhyCiktLeXAgQPExsbicDhq5ZyZmZm0adOGvXv3EhcXVyvnlNqhz6Z+0udSP+lzqZ/q0+diGAZZWVmkpKQQFFTxKA9VQLwEBQXRunXrOjl3XFxcwP/jEN/02dRP+lzqJ30u9VN9+VxOVvmwaBCqiIiI+J0CiIiIiPidAogfhIeHM2XKFMLDwwPdFPGiz6Z+0udSP+lzqZ8a6ueiQagiIiLid6qAiIiIiN8pgIiIiIjfKYCIiIiI3ymAiIiIiN8pgPjB1KlTad++PREREQwbNoylS5cGukmN2rx58xg/fjwpKSk4HA6+/PJLj+cNw+DJJ5+kZcuWREZGMmrUKLZu3epxzPHjx5kwYQJxcXEkJCRw6623kp2d7cd30fg899xzDBkyhNjYWJo3b86ll17K5s2bPY7Jz89n0qRJJCYmEhMTwxVXXMHhw4c9jtmzZw8XXnghUVFRNG/enN/97ncUFxf78600Km+88QZ9+/Z1LWI1fPhwvvvuO9fz+kwC7/nnn8fhcPDAAw+4HmsMn4sCSB375JNPePDBB5kyZQorV66kX79+jB49mrS0tEA3rdHKycmhX79+TJ061efz//d//8crr7zCm2++yZIlS4iOjmb06NHk5+e7jpkwYQIbNmxg9uzZzJgxg3nz5nHHHXf46y00SnPnzmXSpEksXryY2bNnU1RUxAUXXEBOTo7rmN/+9rd88803fPrpp8ydO5cDBw5w+eWXu54vKSnhwgsvpLCwkIULF/Kvf/2LadOm8eSTTwbiLTUKrVu35vnnn2fFihUsX76cc889l0suuYQNGzYA+kwCbdmyZbz11lv07dvX4/FG8bkYUqeGDh1qTJo0yXW/pKTESElJMZ577rkAturUARjTp0933S8tLTWSk5ONF154wfVYenq6ER4ebnz00UeGYRjGxo0bDcBYtmyZ65jvvvvOcDgcxv79+/3W9sYuLS3NAIy5c+cahmF+DqGhocann37qOiY1NdUAjEWLFhmGYRjffvutERQUZBw6dMh1zBtvvGHExcUZBQUF/n0DjViTJk2Mf/7zn/pMAiwrK8vo0qWLMXv2bGPkyJHG/fffbxhG4/nfiiogdaiwsJAVK1YwatQo12NBQUGMGjWKRYsWBbBlp66dO3dy6NAhj88kPj6eYcOGuT6TRYsWkZCQwODBg13HjBo1iqCgIJYsWeL3NjdWGRkZADRt2hSAFStWUFRU5PHZdO/enbZt23p8Nn369KFFixauY0aPHk1mZqbrX+xSfSUlJXz88cfk5OQwfPhwfSYBNmnSJC688EKPvz80nv+taDO6OnT06FFKSko8/gMAaNGiBZs2bQpQq05thw4dAvD5mVjPHTp0iObNm3s8HxISQtOmTV3HSM2UlpbywAMPcMYZZ9C7d2/A/LuHhYWRkJDgcaz3Z+Prs7Oek+pZt24dw4cPJz8/n5iYGKZPn07Pnj1ZvXq1PpMA+fjjj1m5ciXLli0r81xj+d+KAoiI+N2kSZNYv349v/76a6CbIkC3bt1YvXo1GRkZfPbZZ0ycOJG5c+cGulmnrL1793L//fcze/ZsIiIiAt2cOqMumDrUrFkzgoODy4xMPnz4MMnJyQFq1anN+rtX9JkkJyeXGSRcXFzM8ePH9bnVgsmTJzNjxgzmzJlD69atXY8nJydTWFhIenq6x/Hen42vz856TqonLCyMzp07M2jQIJ577jn69evHP/7xD30mAbJixQrS0tIYOHAgISEhhISEMHfuXF555RVCQkJo0aJFo/hcFEDqUFhYGIMGDeKnn35yPVZaWspPP/3E8OHDA9iyU1eHDh1ITk72+EwyMzNZsmSJ6zMZPnw46enprFixwnXMzz//TGlpKcOGDfN7mxsLwzCYPHky06dP5+eff6ZDhw4ezw8aNIjQ0FCPz2bz5s3s2bPH47NZt26dR0CcPXs2cXFx9OzZ0z9v5BRQWlpKQUGBPpMAOe+881i3bh2rV692/QwePJgJEya4fm8Un0ugR8E2dh9//LERHh5uTJs2zdi4caNxxx13GAkJCR4jk6V2ZWVlGatWrTJWrVplAMZLL71krFq1yti9e7dhGIbx/PPPGwkJCcZXX31lrF271rjkkkuMDh06GHl5ea5zjBkzxhgwYICxZMkS49dffzW6dOliXHvttYF6S43C3XffbcTHxxu//PKLcfDgQddPbm6u65i77rrLaNu2rfHzzz8by5cvN4YPH24MHz7c9XxxcbHRu3dv44ILLjBWr15tfP/990ZSUpLx2GOPBeItNQqPPvqoMXfuXGPnzp3G2rVrjUcffdRwOBzGDz/8YBiGPpP6wj4LxjAax+eiAOIHr776qtG2bVsjLCzMGDp0qLF48eJAN6lRmzNnjgGU+Zk4caJhGOZU3CeeeMJo0aKFER4ebpx33nnG5s2bPc5x7Ngx49prrzViYmKMuLg44+abbzaysrIC8G4aD1+fCWC8//77rmPy8vKMe+65x2jSpIkRFRVlXHbZZcbBgwc9zrNr1y5j7NixRmRkpNGsWTPjoYceMoqKivz8bhqPW265xWjXrp0RFhZmJCUlGeedd54rfBiGPpP6wjuANIbPxWEYhhGY2ouIiIicqjQGRERERPxOAURERET8TgFERERE/E4BRERERPxOAURERET8TgFERERE/E4BRERERPxOAURERET8TgFERGpVTk4Of/nLXxg4cCAxMTGEh4fTunVrzjrrLB577DG2b9/uOrZ9+/a0b98+cI0VkYAJCXQDRKTxyMrK4swzz2Tt2rV07tyZ66+/nsTERI4ePcrSpUt5/vnn6dSpE506dQp0U0UkwBRARKTWvPzyy6xdu5bbbruNt99+G4fD4fH8zp07KSgoCFDrRKQ+UReMiNSaRYsWATBp0qQy4QOgQ4cOdO/enV27duFwONi9eze7d+/G4XC4fp566imP18ybN4/x48fTrFkzwsPD6dKlC48//ji5ubkex/3yyy+u1//666+cffbZxMbGkpCQwBVXXMG2bdvKtGfr1q3cfPPNdOjQgfDwcJo2bUq/fv144IEH0DZZInVLFRARqTWJiYkAbNmyhf79+5d7XEJCAlOmTOHll18G4IEHHnA9d/bZZ7t+f+ONN5g0aRIJCQmMHz+e5s2bs3z5cv785z8zZ84c5syZQ1hYmMe5Fy9ezHPPPceYMWO499572bBhA9OnT2f+/PksXryYjh07AnDgwAGGDh1KTk4OF154Iddccw05OTls3bqV119/nRdffJGQEP1fpEidCfBuvCLSiHz11VcGYMTGxhoPPfSQMWvWLOPo0aPlHt+uXTujXbt2Pp/bsGGDERISYvTr16/MOZ577jkDMF588UXXY3PmzDEAAzDefPNNj+PffPNNAzAuuugi12OvvPKKARgvv/xymWsfO3asMm9XRGpAXTAiUmsuvvhi/va3v2EYBn/7298YPXo0zZo1o3PnzkyePJmtW7dW+lxvvfUWxcXFvPrqq67KiuX3v/89SUlJfPTRR2Ve17VrV26//XaPx26//Xa6dOnCzJkzOXLkiMdzkZGRZc7RtGnTSrdTRKrHYRjq6BSR2pWVlcX333/PwoULWb58OUuWLKGoqIiIiAg++eQTLr74YgDXFNxdu3aVOcewYcNYunQpf/zjH312hbzzzjtkZGSQnZ0NmGNAzjnnHG6++Wbee++9MsfffPPNTJs2jdmzZzNq1Ch27dpF7969KSgo4PLLL2fMmDGMHDnS1UUjInVLHZwiUutiY2O56qqruOqqqwDIyMjgD3/4A6+//jq33nor+/fvLzN2w9vx48cB+POf/1yla7do0aLCxzMyMgAz/CxevJinnnqKb7/9lv/9738AdO/enWeeecbVdhGpG+qCEZE6Fx8fz2uvvUa7du04evQo69atO+lr4uLiAMjMzMQwjHJ/vB0+fNjn+azH4+PjXY/17t2bzz77jOPHj7No0SKefPJJDh06xDXXXMOCBQuq81ZFpJIUQETELxwOB9HR0R6PBQcHU1JS4vP4YcOGAeaslqpYsGABpaWlHo+VlpaycOFCHA4H/fr1K/Oa0NBQTjvtNJ5++mleeeUVDMNgxowZVbquiFSNAoiI1Jq33nqLZcuW+Xzuyy+/JDU1lYSEBHr37g2Ygz2PHj1Kfn5+mePvueceQkJCuPfee9mzZ0+Z59PT01m1alWZx7ds2cI777zj8dg777zDli1buPDCC0lKSgJgxYoVZGZmlnm9VSmJiIg4ybsVkZrQGBARqTXfffcdd911F507d+aMM84gJSWFnJwcVq1axfz58wkKCuL1118nPDwcgHPPPZfly5czduxYzjrrLMLCwhgxYgQjRoygd+/evP7669x9991069aNcePG0alTJ7KystixYwdz587lpptu4s033/Row+jRo7nvvvv49ttv6dWrFxs2bOCbb76hWbNm/OMf/3Ad98EHH/DWW28xYsQIOnXqRFxcHBs3buTbb7+ladOm3HzzzX7924mccgI0/VdEGqFNmzYZ//d//2ecf/75RocOHYyIiAgjIiLC6NSpkzFx4kRj+fLlHsdnZWUZt99+u9GyZUsjODjYAIwpU6Z4HLN06VLjN7/5jZGSkmKEhoYazZo1MwYOHGg8+uijRmpqqus4ax2QKVOmGPPnzzdGjhxpREdHG3FxccZll11mbN261eO8ixcvNu68806jd+/eRkJCghEZGWl06dLFmDx5srF79+46+xuJiEnTcEWkUbCm4U6ZMqXMcu4iUv9oDIiIiIj4nQKIiIiI+J0CiIiIiPidxoCIiIiI36kCIiIiIn6nACIiIiJ+pwAiIiIifqcAIiIiIn6nACIiIiJ+pwAiIiIifqcAIiIiIn6nACIiIiJ+pwAiIiIifvf/HiFsb0QDLsAAAAAASUVORK5CYII=\n"
},
"metadata": {}
}
],
"source": [
"data = pd.read_csv(f'logs_csv/lightning_logs/version_{csv_logger.version}/metrics.csv')\n",
"fig, ax = plt.subplots(figsize=(6,5))\n",
"x = data['epoch'][~data['epoch'].isnull()]\n",
"y = data['train_loss'][~data['train_loss'].isnull()]\n",
"print(len(y))\n",
"plt.semilogy(y, label='Training Loss',color='dodgerblue')\n",
"y = data['val_loss'][~data['val_loss'].isnull()]\n",
"print(len(y))\n",
"plt.semilogy(y, label='Validation Loss',color='k')\n",
"plt.xlabel('Steps',size=14)\n",
"plt.ylabel('Loss',size=14)\n",
"plt.legend()"
]
}
],
"metadata": {
"accelerator": "GPU",
"colab": {
"provenance": [],
"include_colab_link": true
},
"kernelspec": {
"display_name": "Python 3",
"name": "python3"
},
"language_info": {
"name": "python"
},
"gpuClass": "standard"
},
"nbformat": 4,
"nbformat_minor": 0
} "
]
},
{
"cell_type": "code",
"source": [
"from IPython.display import HTML\n",
"\n",
"HTML(f\"\"\"\"\"\")"
],
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 321
},
"id": "ljBOLgk-wLWI",
"outputId": "c8595e33-a151-42a8-dc40-29973771c800"
},
"execution_count": 1,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"
"
]
},
{
"cell_type": "code",
"source": [
"from IPython.display import HTML\n",
"\n",
"HTML(f\"\"\"\"\"\")"
],
"metadata": {
"colab": {
"base_uri": "https://localhost:8080/",
"height": 321
},
"id": "ljBOLgk-wLWI",
"outputId": "c8595e33-a151-42a8-dc40-29973771c800"
},
"execution_count": 1,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"