{
"nbformat": 4,
"nbformat_minor": 0,
"metadata": {
"colab": {
"provenance": [],
"include_colab_link": true
},
"kernelspec": {
"name": "python3",
"display_name": "Python 3"
},
"language_info": {
"name": "python"
},
"accelerator": "GPU"
},
"cells": [
{
"cell_type": "markdown",
"metadata": {
"id": "view-in-github",
"colab_type": "text"
},
"source": [
" "
]
},
{
"cell_type": "markdown",
"source": [
"# Lesson 6: DeepPot-Smooth Edition Fitting Neural Network with Machine Learning Potentials (DeepPot-SE-FNN MLP)\n",
"\n",
"$\\Delta$ MLP with PyTorch for the Claisen Rearrangement reaction\n",
"\n",
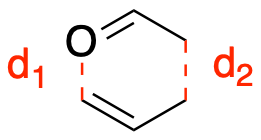
"For this tutorial, we will be combining the Fitting Neural Network (FNN) from Lesson 1 and the DeepPot-Smooth Edition (DeepPot-SE) from Lesson 4 to train a $\\Delta$ Machine Learning Potential ($\\Delta$MLP) model to reproduce the energy and forces for the Claisen Rearrangement reaction. With a DeepPot-SE-FNN, we can utilize the properties from the local environment defined in the DeepPot-SE model for feature extraction and use the FNN for training. The goal of this model is to train with data calculated using semiempirical (PM3) and DFT (B3LYP) levels of theory. The DeepPot-SE-FNN will be used to correct the semiempirical values to obtain DFT level accuracy, that makes it a $\\Delta$MLP model.\n",
"The reaction coordinate is constructed by stretching the $d_2$ bond distance, while shrinking the $d_1$ bond distance. The reaction is sampled with 21 windows along the $d_1-d_2$ reaction coordinate\n",
"\n",
"Total of 2100 frames (1 ps/window) are saved every 1 fs.\n",
"\n",
"
"
]
},
{
"cell_type": "markdown",
"source": [
"# Lesson 6: DeepPot-Smooth Edition Fitting Neural Network with Machine Learning Potentials (DeepPot-SE-FNN MLP)\n",
"\n",
"$\\Delta$ MLP with PyTorch for the Claisen Rearrangement reaction\n",
"\n",
"For this tutorial, we will be combining the Fitting Neural Network (FNN) from Lesson 1 and the DeepPot-Smooth Edition (DeepPot-SE) from Lesson 4 to train a $\\Delta$ Machine Learning Potential ($\\Delta$MLP) model to reproduce the energy and forces for the Claisen Rearrangement reaction. With a DeepPot-SE-FNN, we can utilize the properties from the local environment defined in the DeepPot-SE model for feature extraction and use the FNN for training. The goal of this model is to train with data calculated using semiempirical (PM3) and DFT (B3LYP) levels of theory. The DeepPot-SE-FNN will be used to correct the semiempirical values to obtain DFT level accuracy, that makes it a $\\Delta$MLP model.\n",
"The reaction coordinate is constructed by stretching the $d_2$ bond distance, while shrinking the $d_1$ bond distance. The reaction is sampled with 21 windows along the $d_1-d_2$ reaction coordinate\n",
"\n",
"Total of 2100 frames (1 ps/window) are saved every 1 fs.\n",
"\n",
" \n"
],
"metadata": {
"id": "d5swkZB6PnNA"
}
},
{
"cell_type": "code",
"source": [
"from IPython.display import HTML\n",
"\n",
"HTML(f\"\"\"\"\"\")"
],
"metadata": {
"id": "VOPjmHWg2oQq",
"outputId": "8c4c0278-40ce-4345-c561-dd6df7d25fe5",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 321
}
},
"execution_count": null,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
""
],
"text/html": [
""
]
},
"metadata": {},
"execution_count": 1
}
]
},
{
"cell_type": "markdown",
"source": [
"## Importing PyTorch Lightning and Libraries\n",
"We will first install PyTorch Lightning and import libraries needed to train our machine learning models.\n"
],
"metadata": {
"id": "xbEtVgn-k59m"
}
},
{
"cell_type": "code",
"source": [
"%%capture\n",
"!pip install pytorch-lightning > /dev/null\n",
"\n",
"import math\n",
"import numpy as np\n",
"from typing import Sequence, Tuple\n",
"\n",
"import torch\n",
"import torch.nn as nn\n",
"import torch.nn.functional as F\n",
"from torch import Tensor\n",
"\n",
"from torch.utils.data import TensorDataset, DataLoader, random_split\n",
"import pytorch_lightning as pl\n",
"from pytorch_lightning import loggers as pl_loggers"
],
"metadata": {
"id": "fPn6Q6URnYDN"
},
"execution_count": null,
"outputs": []
},
{
"cell_type": "markdown",
"source": [
"## Defining the Dense Neural Network\n",
"\n",
"The Dense class contains functions to describe a densely connected neural network."
],
"metadata": {
"id": "vHlIa1Bm3Cvp"
}
},
{
"cell_type": "code",
"source": [
"class Sequential(nn.Sequential):\n",
" def forward(self, input: Tuple[Tensor, Tensor]) -> Tuple[Tensor, Tensor]:\n",
" for module in self:\n",
" input = module(input)\n",
" return input\n",
"\n",
"class Dense(nn.Module):\n",
" def __init__(self, num_channels: int, in_features: int, out_features: int, bias: bool = True, activation: bool = False, residual: bool = False) -> None:\n",
" super().__init__()\n",
" self.num_channels = num_channels\n",
" self.in_features = in_features\n",
" self.out_features = out_features\n",
" self.weight = nn.Parameter(torch.Tensor(num_channels, out_features, in_features))\n",
" if bias:\n",
" self.bias = nn.Parameter(torch.Tensor(num_channels, out_features))\n",
" else:\n",
" self.register_parameter('bias', None)\n",
" self.activation = activation\n",
" self.residual = residual\n",
" self.reset_parameters()\n",
"\n",
" def reset_parameters(self) -> None:\n",
" for w in self.weight:\n",
" nn.init.kaiming_uniform_(w, a=math.sqrt(5))\n",
" if self.bias is not None:\n",
" for b, w in zip(self.bias, self.weight):\n",
" fan_in, _ = nn.init._calculate_fan_in_and_fan_out(w)\n",
" bound = 1 / math.sqrt(fan_in)\n",
" nn.init.uniform_(b, -bound, bound)\n",
"\n",
" def forward(self, input: Tuple[Tensor, Tensor]) -> Tuple[Tensor, Tensor]:\n",
" x, channels = input\n",
" weight: Tensor = self.weight[channels]\n",
" output: Tensor = torch.bmm(x.transpose(0, 1), weight.transpose(1, 2)).transpose(0, 1)\n",
"\n",
" if self.bias is not None:\n",
" bias = self.bias[channels]\n",
" output = output + bias\n",
"\n",
" if self.activation:\n",
" output = torch.tanh(output)\n",
"\n",
" if self.residual:\n",
" if output.shape[2] == x.shape[2]:\n",
" output = output + x\n",
" elif output.shape[2] == x.shape[2] * 2:\n",
" output = output + torch.cat([x, x], dim=2)\n",
" else:\n",
" raise NotImplementedError(\"Not implemented\")\n",
"\n",
" return output, channels\n",
"\n",
" def extra_repr(self) -> str:\n",
" return 'num_channels={}, in_features={}, out_features={}, bias={}, activation={}, residual={}'.format(\n",
" self.num_channels, self.in_features, self.out_features, self.bias is not None, self.activation, self.residual\n",
" )"
],
"metadata": {
"id": "v9RdVoWhpVBi"
},
"execution_count": null,
"outputs": []
},
{
"cell_type": "markdown",
"source": [
"## DeepPot-SE Local Environment\n",
"\n",
"Given the atomic coordinates $R$, we can build an environment matrix that describes the local envrionment for each atom $i$ in the molecule. We can then turn the environment matrix into the feature matrix $D_i$ and then map each of the feature matrices into the local energy. This will be done in a manner that preserves translational, rotational, and permutational symmetry. We can obtain our total energy by then summing the local energy values together, which ensures that our total energy is extensive. A schematic of this is shown below:"
],
"metadata": {
"id": "91UJya9WalDP"
}
},
{
"cell_type": "markdown",
"source": [
""
],
"metadata": {
"id": "4w71ewC1OaPB"
}
},
{
"cell_type": "markdown",
"source": [
"First, we build the environment matrix for each atom ${\\tilde{\\mathcal{R}}^i}$\n",
"\n",
"$$\\begin{eqnarray}\n",
"{\\tilde{\\mathcal{R}}^i} = \\begin{pmatrix}\n",
"s(R_{1i}) & s(R_{1i}) \\frac{x_{1i}}{R_{1i}} & s(R_{1i}) \\frac{y_{1i}}{R_{1i}} & s(R_{1i}) \\frac{z_{1i}}{R_{1i}} \\\\ \\\\\n",
"s(R_{2i}) & s(R_{2i}) \\frac{x_{2i}}{R_{2i}} & s(R_{2i}) \\frac{y_{i1}}{R_{2i}} & s(R_{2i}) \\frac{z_{2i}}{R_{2i}} \\\\ \\\\\n",
"\\cdots & \\cdots & \\cdots & \\cdots \\\\ \\\\\n",
"s(R_{n_ii}) & s(R_{n_ii}) \\frac{x_{n_ii}}{R_{n_ii}} & s(R_{n_ii}) \\frac{y_{n_ii}}{R_{n_ii}} & s(R_{n_ii}) \\frac{z_{n_ii}}{R_{n_ii}}\n",
"\\end{pmatrix}\n",
"\\end{eqnarray}$$\n",
"
\n"
],
"metadata": {
"id": "d5swkZB6PnNA"
}
},
{
"cell_type": "code",
"source": [
"from IPython.display import HTML\n",
"\n",
"HTML(f\"\"\"\"\"\")"
],
"metadata": {
"id": "VOPjmHWg2oQq",
"outputId": "8c4c0278-40ce-4345-c561-dd6df7d25fe5",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 321
}
},
"execution_count": null,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
""
],
"text/html": [
""
]
},
"metadata": {},
"execution_count": 1
}
]
},
{
"cell_type": "markdown",
"source": [
"## Importing PyTorch Lightning and Libraries\n",
"We will first install PyTorch Lightning and import libraries needed to train our machine learning models.\n"
],
"metadata": {
"id": "xbEtVgn-k59m"
}
},
{
"cell_type": "code",
"source": [
"%%capture\n",
"!pip install pytorch-lightning > /dev/null\n",
"\n",
"import math\n",
"import numpy as np\n",
"from typing import Sequence, Tuple\n",
"\n",
"import torch\n",
"import torch.nn as nn\n",
"import torch.nn.functional as F\n",
"from torch import Tensor\n",
"\n",
"from torch.utils.data import TensorDataset, DataLoader, random_split\n",
"import pytorch_lightning as pl\n",
"from pytorch_lightning import loggers as pl_loggers"
],
"metadata": {
"id": "fPn6Q6URnYDN"
},
"execution_count": null,
"outputs": []
},
{
"cell_type": "markdown",
"source": [
"## Defining the Dense Neural Network\n",
"\n",
"The Dense class contains functions to describe a densely connected neural network."
],
"metadata": {
"id": "vHlIa1Bm3Cvp"
}
},
{
"cell_type": "code",
"source": [
"class Sequential(nn.Sequential):\n",
" def forward(self, input: Tuple[Tensor, Tensor]) -> Tuple[Tensor, Tensor]:\n",
" for module in self:\n",
" input = module(input)\n",
" return input\n",
"\n",
"class Dense(nn.Module):\n",
" def __init__(self, num_channels: int, in_features: int, out_features: int, bias: bool = True, activation: bool = False, residual: bool = False) -> None:\n",
" super().__init__()\n",
" self.num_channels = num_channels\n",
" self.in_features = in_features\n",
" self.out_features = out_features\n",
" self.weight = nn.Parameter(torch.Tensor(num_channels, out_features, in_features))\n",
" if bias:\n",
" self.bias = nn.Parameter(torch.Tensor(num_channels, out_features))\n",
" else:\n",
" self.register_parameter('bias', None)\n",
" self.activation = activation\n",
" self.residual = residual\n",
" self.reset_parameters()\n",
"\n",
" def reset_parameters(self) -> None:\n",
" for w in self.weight:\n",
" nn.init.kaiming_uniform_(w, a=math.sqrt(5))\n",
" if self.bias is not None:\n",
" for b, w in zip(self.bias, self.weight):\n",
" fan_in, _ = nn.init._calculate_fan_in_and_fan_out(w)\n",
" bound = 1 / math.sqrt(fan_in)\n",
" nn.init.uniform_(b, -bound, bound)\n",
"\n",
" def forward(self, input: Tuple[Tensor, Tensor]) -> Tuple[Tensor, Tensor]:\n",
" x, channels = input\n",
" weight: Tensor = self.weight[channels]\n",
" output: Tensor = torch.bmm(x.transpose(0, 1), weight.transpose(1, 2)).transpose(0, 1)\n",
"\n",
" if self.bias is not None:\n",
" bias = self.bias[channels]\n",
" output = output + bias\n",
"\n",
" if self.activation:\n",
" output = torch.tanh(output)\n",
"\n",
" if self.residual:\n",
" if output.shape[2] == x.shape[2]:\n",
" output = output + x\n",
" elif output.shape[2] == x.shape[2] * 2:\n",
" output = output + torch.cat([x, x], dim=2)\n",
" else:\n",
" raise NotImplementedError(\"Not implemented\")\n",
"\n",
" return output, channels\n",
"\n",
" def extra_repr(self) -> str:\n",
" return 'num_channels={}, in_features={}, out_features={}, bias={}, activation={}, residual={}'.format(\n",
" self.num_channels, self.in_features, self.out_features, self.bias is not None, self.activation, self.residual\n",
" )"
],
"metadata": {
"id": "v9RdVoWhpVBi"
},
"execution_count": null,
"outputs": []
},
{
"cell_type": "markdown",
"source": [
"## DeepPot-SE Local Environment\n",
"\n",
"Given the atomic coordinates $R$, we can build an environment matrix that describes the local envrionment for each atom $i$ in the molecule. We can then turn the environment matrix into the feature matrix $D_i$ and then map each of the feature matrices into the local energy. This will be done in a manner that preserves translational, rotational, and permutational symmetry. We can obtain our total energy by then summing the local energy values together, which ensures that our total energy is extensive. A schematic of this is shown below:"
],
"metadata": {
"id": "91UJya9WalDP"
}
},
{
"cell_type": "markdown",
"source": [
""
],
"metadata": {
"id": "4w71ewC1OaPB"
}
},
{
"cell_type": "markdown",
"source": [
"First, we build the environment matrix for each atom ${\\tilde{\\mathcal{R}}^i}$\n",
"\n",
"$$\\begin{eqnarray}\n",
"{\\tilde{\\mathcal{R}}^i} = \\begin{pmatrix}\n",
"s(R_{1i}) & s(R_{1i}) \\frac{x_{1i}}{R_{1i}} & s(R_{1i}) \\frac{y_{1i}}{R_{1i}} & s(R_{1i}) \\frac{z_{1i}}{R_{1i}} \\\\ \\\\\n",
"s(R_{2i}) & s(R_{2i}) \\frac{x_{2i}}{R_{2i}} & s(R_{2i}) \\frac{y_{i1}}{R_{2i}} & s(R_{2i}) \\frac{z_{2i}}{R_{2i}} \\\\ \\\\\n",
"\\cdots & \\cdots & \\cdots & \\cdots \\\\ \\\\\n",
"s(R_{n_ii}) & s(R_{n_ii}) \\frac{x_{n_ii}}{R_{n_ii}} & s(R_{n_ii}) \\frac{y_{n_ii}}{R_{n_ii}} & s(R_{n_ii}) \\frac{z_{n_ii}}{R_{n_ii}}\n",
"\\end{pmatrix}\n",
"\\end{eqnarray}$$\n",
"
\n",
"\n",
"where $n_i$ is the number of neighbors for atom $i$ and $s$ is the weighting function.\n",
"\n",
"$$\\begin{eqnarray}\n",
"s(R_{ji}) =\n",
"\\begin{cases}\n",
" \\frac{1}{R_{ji}}, & R_{ji} < R_{cs}\\\\\n",
" \\frac{1}{R_{ji}} \\left( \\frac{1}{2} \\cos{\\left[ \\pi \\frac{(R_{ji} - R_{cs})}{(R_{c} - R_{cs})}\\right] + \\frac{1}{2}} \\right), & R_{cs} < R_{ji} < R_{c}\\\\\n",
" 0, & R_{ji} > R_c.\n",
"\\end{cases}\n",
"\\end{eqnarray}$$\n",
"\n",
"The weighting function in the DeepPot-SE scales down the interaction between the atoms $i$ and $j$ as the distance becomes greater than $R_{cs}$ and approaches 0 near the cutoff distance $R_c$. It sets the interaction to 0 for atoms that are beyond the $R_c$ distance. This ensures that $s$ is continuous and differentiable.\n",
"\n",
"We define the $\\,\\it{local\\_environment}\\,$ function below and remove self-interactions."
],
"metadata": {
"id": "VXx_1BbWfY6h"
}
},
{
"cell_type": "code",
"source": [
"def local_environment(coords: Tensor) -> Tuple[Tensor, Tensor]:\n",
" num_batches, num_channels, _ = coords.size()\n",
" rij = coords[:, :, None] - coords[:, None]\n",
" dij = torch.norm(rij, dim=3)\n",
" mask = ~torch.eye(num_channels, dtype=torch.bool, device=coords.device) # remove self-interaction\n",
" rij = torch.masked_select(rij, mask.unsqueeze(2)).view(num_batches, num_channels, num_channels - 1, 3)\n",
" dij = torch.masked_select(dij, mask).view(num_batches, num_channels, num_channels - 1)\n",
" dij_inv = 1 / dij\n",
" dij2_inv = dij_inv * dij_inv\n",
"\n",
" loc_env_r = dij_inv\n",
" loc_env_a = rij * dij2_inv.unsqueeze(3)\n",
"\n",
" return loc_env_r, loc_env_a"
],
"metadata": {
"id": "6CksVhkaqA9e"
},
"execution_count": null,
"outputs": []
},
{
"cell_type": "markdown",
"source": [
"## DeepPot-SE Local Embedding Matrix and Embedded Feature Matrix\n",
"\n",
"After generating the environment matrix, we now need to generate atomic energy components while preserving translational, rotational, and permutational symmetry. The entire DeepPot scheme is presented below:"
],
"metadata": {
"id": "VWTxlndX9WxB"
}
},
{
"cell_type": "markdown",
"source": [
""
],
"metadata": {
"id": "pRbwnQ45d265"
}
},
{
"cell_type": "markdown",
"source": [
"Now we use embedding neural networks to transform each of the $s$ values into $m_1$ numbers. This gives us the local embedding matrix $g_i$. Note the embedding neural network parameters depend on the chemical species of atom $i$ and atom $j$. \n",
"\n",
"$$\\begin{eqnarray}\n",
"g_i\n",
"= \\begin{pmatrix}\n",
"\\left( G[s(R_{1i})] \\right)_1 &\n",
"\\left( G[s(R_{1i})] \\right)_2 & \\cdots &\n",
"\\left( G[s(R_{1i})] \\right)_{m_1} \\\\\n",
"\\left( G[s(R_{2i})] \\right)_1 &\n",
"\\left( G[s(R_{2i})] \\right)_2 & \\cdots & \\left( G[s(R_{2i})] \\right)_{m_1} \\\\\n",
"\\cdots & \\cdots & \\cdots & \\cdots \\\\\n",
"\\left( G[s(R_{n_ii})] \\right)_1 &\n",
"\\left( G[s(R_{n_ii})] \\right)_2 & \\cdots & \\left( G [s(R_{n_ii})] \\right)_{m_1}\n",
"\\end{pmatrix}\n",
"\\end{eqnarray}$$\n",
"\n",
"Two local embedding matrices are used: $g_{i}^{1}$ is $n\\times m_1$ dimensions, while $g_{i}^{2}$ is $n\\times m_2$ dimensions. The dimensions $m_1$ and $m_2$ represent the number of neural network parameters, where $m_1$ is larger than $m_2$.\n",
"\n",
"By multiplying our local embedding matrices and environment matrices, we can preserve the translational, rotational, and permutational symmetry in the form of the encoded feature matrix $D_i$ \n",
"\n",
"$$\\begin{eqnarray}\n",
"D_i = \\left( g_i^1 \\right)^T \\tilde{\\mathcal{R}}^i (\\tilde{\\mathcal{R}}^i)^T g_i^2\n",
"\\end{eqnarray}$$\n",
"\n",
"The local feature matrix is then mapped to the atomic energy using the fitting neural network. Finally, the atomic energies are summed to yield the total energy of the molecule."
],
"metadata": {
"id": "isBWH2DPg3rX"
}
},
{
"cell_type": "markdown",
"source": [
"## Defining Classes for the Neural Network\n"
],
"metadata": {
"id": "QsnXb-EPtTOG"
}
},
{
"cell_type": "markdown",
"source": [
"### The Feature Class\n",
"\n",
"Here we define the feature class, which uses the local environment matrix ($\\tilde{\\mathcal{R}}^i$) and local embedding matrices ($g_{i}^{1}$ and $g_{i}^{2}$) to construct the encoded feature matrix ($D_i$)."
],
"metadata": {
"id": "w7XZmhe7d1gW"
}
},
{
"cell_type": "code",
"source": [
"class Feature(nn.Module):\n",
" def __init__(self, n_types: int, neuron: Sequence[int] = [25, 50, 100], axis_neuron: int = 4) -> None:\n",
" super().__init__()\n",
" self.n_types = n_types\n",
" self.neuron = neuron\n",
" self.axis_neuron = axis_neuron\n",
"\n",
" layers = [Dense(n_types * n_types, 1, neuron[0], activation=True)]\n",
" for i in range(len(neuron)-1):\n",
" layers.append(Dense(n_types * n_types, neuron[i], neuron[i+1], activation=True, residual=True))\n",
" self.local_embedding = Sequential(*layers)\n",
"\n",
" def forward(self, coords: Tensor, atom_types: Tensor) -> Tensor:\n",
" num_batches, num_channels, _ = coords.size()\n",
" loc_env_r, loc_env_a = local_environment(coords)\n",
"\n",
" neighbor_types = atom_types.repeat(num_channels, 1)\n",
" mask = ~torch.eye(num_channels, dtype=torch.bool, device=coords.device)\n",
" neighbor_types = torch.masked_select(neighbor_types, mask).view(num_channels, -1)\n",
" indices = ((atom_types * self.n_types).unsqueeze(-1) + neighbor_types).view(-1)\n",
"\n",
" output, _ = self.local_embedding((loc_env_r.view(num_batches, -1, 1), indices))\n",
" output = output.view(num_batches, num_channels, num_channels - 1, -1)\n",
"\n",
" output = torch.transpose(output, 2, 3) @ (loc_env_a @ (torch.transpose(loc_env_a, 2, 3) @ output[..., :self.axis_neuron]))\n",
" output = output.view(num_batches, num_channels, -1)\n",
"\n",
" return output\n",
"\n",
" @property\n",
" def output_length(self) -> int:\n",
" return self.neuron[-1] * self.axis_neuron"
],
"metadata": {
"id": "WY8A0MmNqnvM"
},
"execution_count": null,
"outputs": []
},
{
"cell_type": "markdown",
"source": [
"### The Fitting Class\n",
"\n",
"Now we define the fitting neural network that maps the encoded feature matrix into the atomic energy values."
],
"metadata": {
"id": "DItPRorUd_Dq"
}
},
{
"cell_type": "code",
"source": [
"class Fitting(nn.Module):\n",
" def __init__(self, n_types: int, in_features: int, neuron: Sequence[int] = [240, 240, 240]) -> None:\n",
" super().__init__()\n",
" layers = [Dense(n_types, in_features, neuron[0], activation=True)]\n",
" for i in range(len(neuron)-1):\n",
" layers.append(Dense(n_types, neuron[i], neuron[i+1], activation=True, residual=True))\n",
" layers.append(Dense(n_types, neuron[-1], 1))\n",
" self.fitting_net = Sequential(*layers)\n",
"\n",
" def forward(self, input : Tuple[Tensor, Tensor]) -> Tensor:\n",
" output, _ = self.fitting_net(input)\n",
" return output"
],
"metadata": {
"id": "KWF2_lClqvpN"
},
"execution_count": null,
"outputs": []
},
{
"cell_type": "markdown",
"source": [
"### The DeepPot Class\n",
"\n",
"We define the DeepPot class to extract features from a data set using local environment properties for training a neural network model."
],
"metadata": {
"id": "SmDHvqObmv0v"
}
},
{
"cell_type": "code",
"source": [
"class DeepPot(pl.LightningModule):\n",
" def __init__(self, descriptor: nn.Module, fitting_net: nn.Module, learning_rate=5e-4) -> None:\n",
" super().__init__()\n",
" self.descriptor = descriptor\n",
" self.fitting_net = fitting_net\n",
" self.learning_rate = learning_rate\n",
"\n",
" def forward(self, coords: torch.Tensor, atom_types: torch.Tensor):\n",
" coords.requires_grad_()\n",
" descriptors = self.descriptor(coords, atom_types)\n",
" atomic_energies = self.fitting_net((descriptors, atom_types))\n",
" energy = torch.unbind(torch.sum(atomic_energies, dim=1))\n",
" gradient, = torch.autograd.grad(energy, [coords], create_graph=True)\n",
" return torch.hstack(energy), gradient\n",
"\n",
" def training_step(self, batch, batch_idx):\n",
" qm_coord, atom_types, energy, gradient = batch\n",
" ene_pred, grad_pred = self(qm_coord, atom_types[0])\n",
" ene_loss = F.mse_loss(ene_pred, energy)\n",
" grad_loss = F.mse_loss(grad_pred, gradient)\n",
"\n",
" lr = self.optimizers().optimizer.param_groups[0]['lr']\n",
" start_lr = self.optimizers().optimizer.param_groups[0]['initial_lr']\n",
" w_ene = 1\n",
" w_grad = 1 + 99 * (lr / start_lr)\n",
"\n",
" loss = w_ene / (w_ene + w_grad) * ene_loss + w_grad / (w_ene + w_grad) * grad_loss\n",
" self.log('train_loss', loss)\n",
" self.log('l2_trn', torch.sqrt(loss))\n",
" self.log('l2_e_trn', torch.sqrt(ene_loss))\n",
" self.log('l2_f_trn', torch.sqrt(grad_loss))\n",
" return loss\n",
"\n",
" def validation_step(self, batch, batch_idx):\n",
" torch.set_grad_enabled(True)\n",
" qm_coord, atom_types, energy, gradient = batch\n",
" ene_pred, grad_pred = self(qm_coord, atom_types[0])\n",
" ene_loss = F.mse_loss(ene_pred, energy)\n",
" grad_loss = F.mse_loss(grad_pred, gradient)\n",
"\n",
" lr = self.optimizers().optimizer.param_groups[0]['lr']\n",
" start_lr = self.optimizers().optimizer.param_groups[0]['initial_lr']\n",
" w_ene = 1\n",
" w_grad = 1 + 99 * (lr / start_lr)\n",
"\n",
" loss = w_ene / (w_ene + w_grad) * ene_loss + w_grad / (w_ene + w_grad) * grad_loss\n",
" self.log('val_loss', loss)\n",
" self.log('l2_tst', torch.sqrt(loss))\n",
" self.log('l2_e_tst', torch.sqrt(ene_loss))\n",
" self.log('l2_f_tst', torch.sqrt(grad_loss))\n",
" self.log('lr', lr)\n",
" return loss\n",
"\n",
" def configure_optimizers(self):\n",
" optimizer = torch.optim.Adam(self.parameters(), lr=self.learning_rate)\n",
" scheduler = {'scheduler': torch.optim.lr_scheduler.ExponentialLR(optimizer, 0.95),\n",
" 'interval': 'epoch',\n",
" 'frequency': 10,\n",
" }\n",
" return [optimizer], [scheduler]"
],
"metadata": {
"id": "xM95a2o2hGVf"
},
"execution_count": null,
"outputs": []
},
{
"cell_type": "markdown",
"source": [
"## Importing Data and Feature Extraction\n",
"\n",
"We will now import our semiempirical and DFT calculation data, which will be used by the DeepPot model for feature extraction. We will then use seeding to generate random but reproducible training.\n"
],
"metadata": {
"id": "8QkDejGJmcMC"
}
},
{
"cell_type": "code",
"source": [
"%%capture\n",
"import numpy as np\n",
"\n",
"ds = np.DataSource(None)\n",
"qm_coord = np.array(np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_coord.npy\", \"rb\")), dtype=\"float32\")\n",
"atom_types = np.loadtxt(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_elem.txt\", \"r\"), dtype=int)\n",
"elems = np.unique(atom_types).tolist()\n",
"atom_types = np.array([[elems.index(i) for i in atom_types]])\n",
"atom_types = atom_types.repeat(len(qm_coord), axis=0)\n",
"\n",
"energy = np.array((np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy.npy\", \"rb\")) - np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy_sqm.npy\", \"rb\"))) * 27.2114 * 23.061, dtype=\"float32\")\n",
"energy = energy - energy.mean()\n",
"qm_gradient = np.array((np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad.npy\", \"rb\")) - np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad_sqm.npy\", \"rb\"))) * 27.2114 * 23.061 / 0.529177249, dtype=\"float32\")\n",
"\n",
"device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')\n",
"\n",
"qm_coord = torch.from_numpy(qm_coord).to(device)\n",
"atom_types = torch.from_numpy(atom_types).to(device)\n",
"energy = torch.from_numpy(energy).to(device)\n",
"qm_gradient = torch.from_numpy(qm_gradient).to(device)"
],
"metadata": {
"id": "tDm7RmYwns4J"
},
"execution_count": null,
"outputs": []
},
{
"cell_type": "code",
"source": [
"pl.seed_everything(2)\n",
"dataset = TensorDataset(qm_coord, atom_types, energy, qm_gradient)\n",
"train, val = random_split(dataset, [2016, 84])\n",
"# Training Set Size: 2016 (96%)\n",
"# Test Set Size: 84 ( 4%)\n",
"# Data Set Size: 2100\n",
"train_loader = DataLoader(train, batch_size=32)\n",
"val_loader = DataLoader(val, batch_size=32)"
],
"metadata": {
"id": "NuF4V-SznyyJ",
"colab": {
"base_uri": "https://localhost:8080/"
},
"outputId": "c2758c86-3093-4e1d-f1d6-590669816da8"
},
"execution_count": null,
"outputs": [
{
"output_type": "stream",
"name": "stderr",
"text": [
"INFO:lightning_fabric.utilities.seed:Global seed set to 2\n"
]
}
]
},
{
"cell_type": "markdown",
"source": [
"### Training the Neural Network\n",
"\n",
"Now we begin training our NN using the training and validation datasets.\n"
],
"metadata": {
"id": "VSxXL1bim18I"
}
},
{
"cell_type": "code",
"source": [
"%%capture\n",
"%%time\n",
"pl.seed_everything(2)\n",
"descriptor = Feature(3, neuron=[25, 50, 100], axis_neuron=4)\n",
"fitting_net = Fitting(3, descriptor.output_length)\n",
"model = DeepPot(descriptor, fitting_net, learning_rate=5e-4)\n",
"csv_logger = pl_loggers.CSVLogger('logs_csv/')\n",
"trainer = pl.Trainer(max_epochs=300, logger=csv_logger, log_every_n_steps=20, accelerator='auto')\n",
"trainer.fit(model, train_loader, val_loader)\n",
"model.to(device)"
],
"metadata": {
"id": "1uJoAwQNoGBk",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 306
},
"outputId": "16b18062-cbc7-4a1a-c0a0-a21db5ca39fd"
},
"execution_count": null,
"outputs": [
{
"output_type": "stream",
"name": "stderr",
"text": [
"INFO:lightning_fabric.utilities.seed:Global seed set to 2\n",
"INFO:pytorch_lightning.utilities.rank_zero:GPU available: True (cuda), used: True\n",
"INFO:pytorch_lightning.utilities.rank_zero:TPU available: False, using: 0 TPU cores\n",
"INFO:pytorch_lightning.utilities.rank_zero:IPU available: False, using: 0 IPUs\n",
"INFO:pytorch_lightning.utilities.rank_zero:HPU available: False, using: 0 HPUs\n",
"INFO:pytorch_lightning.accelerators.cuda:LOCAL_RANK: 0 - CUDA_VISIBLE_DEVICES: [0]\n",
"INFO:pytorch_lightning.callbacks.model_summary:\n",
" | Name | Type | Params\n",
"----------------------------------------\n",
"0 | descriptor | Feature | 58.1 K\n",
"1 | fitting_net | Fitting | 636 K \n",
"----------------------------------------\n",
"694 K Trainable params\n",
"0 Non-trainable params\n",
"694 K Total params\n",
"2.778 Total estimated model params size (MB)\n",
"INFO:pytorch_lightning.utilities.rank_zero:`Trainer.fit` stopped: `max_epochs=300` reached.\n"
]
}
]
},
{
"cell_type": "markdown",
"source": [
"### Saving the Model to a PyTorch File\n",
"\n",
"The following files are saved:\n",
"\n",
"**1) model.pt**\n",
"- torch.save saves tensors to model.pt\n",
"\n",
"**2) model_script.pt**\n",
"- torch.jit.save attempts to preserve the behavior of some operators across PyTorch versions.\n",
"\n",
"\n",
"Previously saved models can be loaded with:\n",
" - model.load_state_dict(torch.load(\"model.pt\"))\n",
" - torch.jit.load(\"model_script.pt\")"
],
"metadata": {
"id": "FxM6WjAvm6XV"
}
},
{
"cell_type": "code",
"source": [
"torch.save(model.state_dict(), 'model.pt')\n",
"torch.jit.save(model.to_torchscript(), \"model_script.pt\")"
],
"metadata": {
"id": "4XkVxKCQoJ4Y"
},
"execution_count": null,
"outputs": []
},
{
"cell_type": "code",
"source": [
"ene_pred, grad_pred = model(qm_coord, atom_types[0])"
],
"metadata": {
"id": "xYgBIF-LpXi6"
},
"execution_count": null,
"outputs": []
},
{
"cell_type": "markdown",
"source": [
"## Plotting RMSD for the $\\Delta$MLP and Training Errors"
],
"metadata": {
"id": "727IlytNnQLx"
}
},
{
"cell_type": "markdown",
"source": [
"### Plotting RMSD for $\\Delta$MLP Energy and Forces\n",
"RMSD for predicted and reference energy and forces are calculated and displayed below."
],
"metadata": {
"id": "edOA63_q2hDF"
}
},
{
"cell_type": "code",
"source": [
"import matplotlib.pyplot as plt\n",
"\n",
"fig, ax = plt.subplots(2,figsize=(6,10))\n",
"\n",
"e1 = energy.cpu().detach().numpy() + np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy_sqm.npy\",\"rb\")) * 27.2114 * 23.061\n",
"e2 = ene_pred.cpu().detach().numpy() + np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy_sqm.npy\",\"rb\")) * 27.2114 * 23.061\n",
"ax[0].plot(e1, e2, linestyle='none', marker='.', color='springgreen')\n",
"ax[0].plot([np.max(e1), np.min(e1)], [np.max(e2), np.min(e2)] , color=\"k\", linewidth=1.5)\n",
"ax[0].set_xlabel(\"Reference Energy (kcal/mol)\", size=14)\n",
"ax[0].set_ylabel(\"Predicted Energy (kcal/mol)\", size=14)\n",
"ax[0].annotate('RMSD: %.3f' % np.sqrt(np.mean((e1 - e2)**2)), xy=(0.05, 0.95), xycoords='axes fraction', size=14)\n",
"\n",
"f1 = -qm_gradient.cpu().detach().numpy().reshape(-1) - np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad_sqm.npy\",\"rb\")).reshape(-1) * 27.2114 * 23.061 / 0.529177249\n",
"f2 = -grad_pred.cpu().detach().numpy().reshape(-1) - np.load(ds.open(\"https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad_sqm.npy\",\"rb\")).reshape(-1) * 27.2114 * 23.061 / 0.529177249\n",
"\n",
"ax[1].plot(f1, f2, linestyle='none', marker='.', color='springgreen')\n",
"ax[1].plot([np.max(f1), np.min(f1)], [np.max(f2), np.min(f2)] , color=\"k\", linewidth=1.5)\n",
"ax[1].set_xlabel(r'Reference Force (kcal/mol/$\\AA$)', size=14)\n",
"ax[1].set_ylabel(r'Predicted Force (kcal/mol/$\\AA$)', size=14)\n",
"ax[1].annotate('RMSD: %.3f' % np.sqrt(np.mean((f1 - f2)**2)), xy=(0.05, 0.95), xycoords='axes fraction', size=14)\n",
"\n",
"plt.tight_layout()\n",
"plt.savefig('rmsd.png', dpi=300)"
],
"metadata": {
"id": "qedW96hrpZFF",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 1000
},
"outputId": "af762456-df5f-4e4b-f44e-4a0ab2c8cb09"
},
"execution_count": null,
"outputs": [
{
"output_type": "display_data",
"data": {
"text/plain": [
""
],
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAk4AAAPdCAYAAAB83OesAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOzdd3gUZdvG4d8mkFATCL33D0QQBSmhg0DoHcWClEgTkSYgiqK+Kigqgh2JFJWuUgRBQJp0KYoISAklQAAJbCBAAsl8fyy7ZJNNsmm7Kdd5HDled2Z25tmF11w+88x9mwzDMBARERGRJHm4ewAiIiIimYWCk4iIiIiTFJxEREREnKTgJCIiIuIkBScRERERJyk4iYiIiDhJwUlERETESTncPYCsLCYmhvPnz5M/f35MJpO7hyMiIiIOGIbB9evXKVmyJB4eic8pKTilo/Pnz1OmTBl3D0NERESccPbsWUqXLp3oMQpO6Sh//vyA5Q/Cx8fHzaMRERERR8LDwylTpozt93ZiFJzSkfX2nI+Pj4KTiIhIBufMshotDhcRERFxkoKTiIiIiJMUnEREREScpOAkIiIi4iQFJxEREREnKThlEadOncJkMtn95MyZk1KlSvH444/zxx9/OHxfv379bMd/+umnCZ7/iSeesB03Z84cu32GYfDdd9/RsmVLChUqhJeXF8WKFeORRx7h+eefZ/PmzXbHv/HGG3bj9PT0pECBAvzf//0fvXr1Yvbs2URERKT6O4ntwoULBAYGUqJECXLlykXVqlV55513uHPnjtPniP1dJfTzv//9L9FzLFq0yHbswoULHR4TGRnJW2+9RZUqVciVKxclS5Zk0KBBXLp0KVmfWURE0p7KEWQxlSpV4plnngEgIiKCvXv3smTJEpYtW8b69etp2rSpw/flyJGDb775hhdeeCHevrCwMJYvX06OHDm4e/duvP0DBgxgzpw5FCxYkI4dO1KqVClu3brFn3/+SVBQEOHh4TRr1ize+3r06EGNGjUASw2NU6dOsWnTJpYuXcrrr7/Ot99+S/PmzVPxbViEhoZSv359QkJC6NatG1WqVGHz5s1MnDiR3bt3s2zZMqceQe3atSvly5d3uO+DDz4gIiKCgICARMcxbNgw8ubNm2AwjImJoUuXLqxdu5YGDRrQo0cPjh07xqxZs9iwYQM7d+6kSJEiTn1uERFJB4akG7PZbACG2WxO92sFBwcbgBEQEBBv3+TJkw3AaNq0abx9ffv2NQCjU6dOBmAcOHAg3jHTp083AKNz584GYMyePdu2b8uWLQZgPPzwww4/59WrV41t27bZbZs0aZIBGAsWLIh3/O3bt40pU6YYHh4eRt68eY0///zTmY+fqGeffdYAjC+++MK2LSYmxujdu7cBGPPnz0/V+f/44w8DMGrWrJnocZ06dTLKly9vjBkzJsHP/8033xiA8eSTTxoxMTG27V988YUBGIMGDUrVWEVEJL7k/L7WrbpsIDAwEIC9e/cmeEzfvn3x9PQkKCgo3r7Zs2fzwAMP4O/vH2/fjh07bO93VOSzQIECNGzY0Omxent7M378eF5//XUiIiJ4+eWXnX6vI9evX2fRokVUrFiRwYMH27abTCamTJkCwNdff52qa1i/M+v37MicOXNYuXIls2bNIl++fAkeZx3L5MmT7WbBBg8eTMWKFfn++++5detWqsYrIiIpp+CUjeTIkfCd2VKlStGmTRvmz59PVFSUbfu+ffs4cOAA/fv3d/i+QoUKAfDvv/+m6VjHjBlDnjx5WLt2LWaz2bZ906ZNmEwmp2/h7dixg8jISFq3bh3vdly5cuWoWrUq27ZtIzo6OkXjvHXrFvPnz8fb25s+ffo4PObs2bOMHDmSQYMG8dhjjyV4rtu3b7Nr1y6qVq1KuXLl7PaZTCZat25NREREguvVREQk/Sk4ZQOzZs0CoHHjxokeFxgYyJUrV1i+fLltW1BQEDly5ODZZ591+J6AgAB8fHz48ssvefrpp1m6dCmnT59O9Zjz5ctHnTp1iImJSXSmLCnHjh0DoEqVKg73V6lShaioqBSPeenSpZjNZrp164afn1+8/YZhEBgYiI+PDx988EGi5zpx4gQxMTGJjhXufyYREXE9LQ7PYo4fP84bb7wB3F8cvnHjRooVK8bUqVMTfW/nzp0pXLgw33zzDb169eL27dssWLCADh06UKxYMYfvKV26ND/88AOBgYHMnz+f+fPnA1CkSBFatGjB4MGDadmyZYo+S8mSJQH477//bNvq1avH4cOHyZMnj1PnsM5W+fr6Otxvvb0Ye1YrOay36Z577jmH+7/88kvWrVvHmjVrkmwemd5jFRGR1FNwymJOnDjBm2++abetePHibN26lcqVKyf63pw5c/LMM88wY8YMzp07x5YtW7h69SoDBgxI9H2tWrXixIkTbNq0iS1btrB3715+//13Fi9ezOLFi5kwYQLvvvtuqj8bQJ48eahWrVqanCu1jh8/zpYtW6hQoYLDcHjy5EnGjh3LgAEDEn3aTkREMg/dqstiAgICMAwDwzC4dOkSU6dO5dKlS3Tu3JkbN24k+f4BAwYQExPDnDlz+OabbyhevDjt27dP8n05cuSgVatWvPXWW6xatYorV67w9ddfkyNHDiZPnsy+ffuS/VnOnz8PkKrH762zNwnN0oSHh9sdlxzffPMNhmEwYMAAh+UMAgMDKVCgAB999JHbxyoikhWEYGYjwYTgvpl3BacsrEiRIrz00ku88sorHD58mIkTJyb5npo1a1K3bl0+++wzfvvtN5599tlEF5UnJEeOHDz33HM89dRTAGzcuDFZ779x4wZ79+7F09OT2rVrJ/v6VkmtCzp27BheXl6ULVs2WeeNjo5m7ty5eHp6Jrhwfv/+/Zw7d44CBQrYFcm0zgg++eSTmEwmPv74YwAqVqyIh4dHomON/ZlERLKTIPZRNvojWjKXcnxMEMn/D/K0oFt12cArr7zCN998w+eff87IkSMTLOJoNWDAAIYOHWr759RI7NH7xHz44YfcvHmTjh07pmqGpUGDBnh5ebFu3ToMw7CbGTp9+jRHjx6lRYsWyQ6Hq1ev5vz583To0IFSpUo5PObZZ5/l5s2b8bbv27eP/fv306JFCypWrGgrApo7d27q1avHzp07OX36tN2TdYZhsG7dOvLmzcujjz6arLGKiGR2IZgZeOZbjC4L4d2WxLSrwmBWEkAlSuPaWXgFp2wgd+7cjB8/nhEjRvC///3PYa2m2J555hmKFy9ua02SmDVr1hAZGUmHDh3ihY/jx4+zZMkSIOkn+qwiIyOZPn06b731Fvny5WPy5Ml2+2/evMmZM2fIkyePU7NEPj4+9O7dm3nz5vHVV18xZMgQwBJEJkyYAMDAgQPt3mM2m7lw4QK+vr6UKFHC4Xmdqd00Y8YMh9vfeOMN9u/fz6BBg+jdu7fdvkGDBrFz504mTJjA999/bwt6X331FSdPnmTQoEHkzp07yc8tIpKVrNq3BaPjLLhwA0auhdaViM7hwXHCFJwkfQwaNIj33nuPefPm8corr1CpUqUEj82XLx9du3Z16rxHjhxh1KhRFC5cmKZNm1KpUiUMw+D48eOsXr2aqKgohg4dSv369eO9d+nSpRw5cgSw3JoLDg5my5Yt/Pfff5QpU4bvvvvONhtjtXv3blq0aEGzZs3YtGmTU2OcMmUKGzdu5Pnnn2f9+vVUrlyZzZs3s3PnTjp16hQvvPz000/079+fvn37xuvLB3Dx4kVWrVpFsWLF6NSpk1NjcFbfvn1ZtGgRCxYsIDg4mGbNmnH8+HF+/PFHKlSowNtvv52m1xMRyehWrVrF6CeehIgIqFEUVj0FOTzwxERl4peBSW8KTtlErly5mDBhAsOHD+fNN99k3rx5aXLep59+mnz58rF27VoOHjzIunXruH37NoULF6ZNmzb069ePHj16OHzvDz/8wA8//ICHhwf58uWjaNGiNG/enA4dOvD44487XXIgKSVKlGDXrl1MnDiRVatWsXLlSsqVK8f//vc/xo0b51Sfutjmzp3L3bt36du3b4rWfyXGw8OD5cuXM2XKFL799lumTZuGn58fgYGBvP322+pTJyLZyueff87w4cOJiYnhgVb1Obq0BTG+3nhi4is6uXy2CcBkGIbh8qtmE+Hh4fj6+mI2mx22IxEREZH4YmJiGD9+vK1w8IABA/jyyy+5mPMmxwmjMn5pGpqS8/taM04iIiKSYdy6dYs+ffrwww8/APD222/zyiuvYDKZKI2vW2aZYlNwEhERkQzh8uXLdO7cmZ07d+Ll5cXs2bNtZW0yCgUnERERcbujR4/Svn17Tp48ScGCBVm2bBlNmzZ197DiUXASERERt9q6dStdunTh6tWrVKhQgV9++SXJcjjuosrhIiIi4jbz58+nVatWXL16lfr167Nz584MG5pAwUlERETcwDAM3n33XZ5++mmioqLo3r07GzdupGjRou4eWqIUnERERMSl7ty5w8CBA3n11VcBGDNmDEuWLMkUnRG0xklERERcxmw206tXL9atW4eHhwczZsxg2LBh7h6W0xScRERExCXOnj1Lhw4dOHjwIHny5GHRokV07NjR3cNKFgUnERERSXf79++nQ4cOXLhwgeLFi/Pzzz9Tp04ddw8r2bTGSURERNLV6tWradKkCRcuXODBBx9k165dmTI0gYKTiIiIpKMvvviCTp06ERERQatWrdi2bRtly5Z197BSTMFJRERE0lxMTAxjx47l+eefJyYmhv79+7N69Wp8fd3bay61tMZJRERE0tStW7d49tlnWbp0KWDfqDezU3ASERGRNBO3Ue8333zD008/7e5hpRkFJxEREUkT//77L+3atbM16v3pp59o1qyZu4eVprTGSURERFJt69at+Pv7c/LkSSpUqMD27duzXGgCBScRERFJpQULFtCqVSvCwsJsjXqrVavm7mGlCwUnERERSRHDMJg8eTJPPfUUUVFRdOvWjd9++y3DN+pNDQUnERERSTZro95XXnkFgNGjR7NkyRLy5Mnj5pGlLy0OFxERkWQJDw+nZ8+embZRb2ooOImIiIjTskKj3tRQcBIRERGn7N+/n44dO3L+/PlM3ag3NbTGSUREJBsLwcxGggnBnOhx1ka958+fz/SNelNDwUlERCSbCmIf5fiYlsylHB8TxD6Hx3355ZdZqlFvaig4iYiIZEMhmBnESmIwAIjBYDArCcFsm4U6E3OVcePGMXTo0CzVqDc1tMZJREQkGzpGmC00WUVjMJ1dfMQOYm5FwbPLYOk/APzvf//j1VdfzRKNelNDM073TJkyBZPJxMiRI23bbt++zbBhwyhUqBD58uWjR48eXLx40X2DFBERSSNV8MMD+xDkAZbQdPkGPDbPEpq8PJnx3UwmTpyY7UMTKDgBsGfPHr766iseeughu+2jRo1i5cqVLFmyhM2bN3P+/Hm6d+/uplGKiIikndL4MpNOeN4LT56YGE1DYv79DxoEwY4QKJgLfn2Gmk+3cvNoM45sH5xu3LjB008/zddff03BggVt281mM0FBQXz00Ue0bNmSOnXqMHv2bLZv387OnTvdOGIREZG0EUhtTjGSjfTlFCNpsDUa/IPg5FWoUAC2B+LZrAKV8XP3UDOMbB+chg0bRocOHWjVyj5N7927lzt37thtr1atGmXLlmXHjh0OzxUZGUl4eLjdj4iISEYVgpljhFEZP7YuWM1TrbpC2C2oXwp2PodntSJ8RSdKk30Xg8eVrReHL1y4kH379rFnz554+0JDQ/Hy8qJAgQJ224sVK0ZoaKjD802ePJk333wzPYYqIiKSpoLYZ3mqzojBNGUbxisbAOjWrRvvffcZ5/LcpjJ+Ck1xZNsZp7NnzzJixAi+//57cuXKlSbnnDBhAmaz2fZz9uzZNDmviIhIWgnBzGL+toSmO3dh0EpbaBo4ehhLliyhSp4SNKeCQpMD2XbGae/evVy6dInatWvbtkVHR7NlyxY+/fRT1q5dS1RUFNeuXbObdbp48SLFixd3eE5vb2+8vb3Te+giIiIpYptlwoDwSOi1BH49AR4mmNGWp4aNwRNPdw8zQ8u2wemxxx7j4MGDdtv69+9PtWrVGD9+PGXKlCFnzpxs2LCBHj16AHD06FHOnDmDv7+/O4YsIiKSYnYFL8+aocN8OHgJ8uSERT3x7FhVi8CdkG2DU/78+alRo4bdtrx581KoUCHb9sDAQEaPHo2fnx8+Pj4MHz4cf39/GjRo4I4hi4iIpJit4OWBUEtoOn8diueDn5/Es04pLQJ3UrYNTs6YNm0aHh4e9OjRg8jISAICAvj888/dPSwRERGnWJ+aq4IfVfCD1cfgiaVwIwoeLAKrnmJxuefwp4xCk5NMhmEYSR8mKREeHo6vry9msxkfHx93D0dERLKR2OuZPDDR5csb/DTsQ4gx4LEK8MPjePjmZieB3OAOVbLxE3TJ+X2tGScREZEMKvaMkbOhJgQz2znLQFZYOtHFGMS8vI6fpm63HNDvYfiqI3h5EoNBfWZhAB6YmEknAqmd8MlFwUlERCQjijtj5Eyomco2xrPufuveW3eg7zJYYmnUy/9awKtNIFbPOeuxMRgMZiUBVMq2M0/OyLZ1nERERDIquyfguB9qQjAn+J4P2Ma42KHpcoSlUe+SfyCnB3zbDSY2tYWmuA1+AaIxOE5YWn+cLEXBSUREJIOxPQEXS2KhJgQz41l/f8O/Vyw953aEQIFcsK4PPHO/kf00AthJYLzw5IlJJQmSoOAkIiKSwVTBL1mhxi5o/X7GEppOWBv1DoBm5e2O38ZZ6lKamXTC8951PDGpJIETtMZJREQkgymNLzPpxGBWEo2RZKipgh8mwFj4t2VNU1Q01CsFK5+EonnjHb+Uf9hDCIHUJoBKHL/X6FehKWkKTiIiIhlE7KfokhNqDMPAeO93mGDpOUe3avBdd0tV8ARYZ51K46vAlAwKTiIiIhlAQk/RWUNNQqUJ7ty5w5Dnh8Cse6FpVAOY2ho8E1+N04gy6fZZsjIFJxERETdL6Cm6hyjKDe6wl/OMZ328UBUeHk6nXt3Y8utvlka909vCC/WSvF5falGX0un9sbIkBScRERE3S+gpugYExdtuDVVRIWG81X4IoQdPWG7JLewBnaomeA0PoCcP8hL+Ck2poOAkIiLiZtan6ByFJEeiD1zg+Q7d7Rr1UqdkguefRgA9qa61TGlA5QhERETczPoUnbU0QKK/nH85Bk1mW0LTg0VgZ2CiockTk0JTGtKMk4iISAYQ+ym6vOR0eJuOr/6AYash2oCWlka9FMiV4DlVmyntKTiJiIhkELFLA8Su40SMARPWw/vxG/U60pMHGEY91WZKBwpOIiIiGVAgtdnDOb66tdO+Ue9bze16zsXlgYm2VKE5FVw21uxEa5xEREQyoD2E8NV/W6HVt/aNel9rlmBoAucaAkvKKTiJiIi4QQhmNhLsMOAEsY96x96z9JzbftayjulX+0a9iUmsIbCkjoKTiIiIiwWxj3J8TEvmUo6PCWIfYAlTX7Cb537/FBoEwfEwKF/A0qi3eXmH55pEs2Q1BJbU0RonERERF3JUJXwQKzjJVSazFWPR3/DssvuNelf0hmL5HJ7LExPPUZsy+DrdEFhSR8FJRETEhRxVCY8B3jW2wHvbEm3Ua5lZMojBvtRAchoCS+q4PTiZzWby5MlDzpwJd3AWERHJKhxWCb8TbanP9LXllp2jRr3WoJRQQIpdykDSj0uD040bN1iyZAkbNmxg27ZtnD9/nrt37wKQP39+atasSfPmzenSpQuPPvqoK4cmIiLiEtYq4YNYQQxAeCQ8vgTWnki0Ue/LNCaQ2rZziHuYDMNw3AgnDZ09e5a3336bBQsWcOPGDQAKFixIsWLF8PPz49atW4SFhRESEkJ0dDQmk4mHH36Y0aNH8/TTT6f38NJNeHg4vr6+mM1mfHx83D0cERHJIEIwM48DvBqyHDrMh78uJtmo1wMTpxmp0JQOkvP7Ot1nnF5++WVmzJhBdHQ07dq14/HHH8ff358KFeIX5rp58yZ79+7l119/Zf78+fTp04dp06bx9ddf88gjj6T3UEVERNJdEPsYyAqMA6GW0ORko96YeyUGFJzcK91nnAoUKMCLL77IyJEj8fNL3qOR69ev56233qJVq1a8/vrr6TTC9KMZJxERiS0EM2WZhvHLMXh8KdyIsjTqXfUUlCuQ6Hs9MXFKM07pIkPNOAUHB1OwYMEUvbdVq1a0atWKq1evpvGoREREXCcEM9s5y3bOYiSjUa/lGTo1681I0j04pTQ0pfU5RERE3OEDtjGWdclu1AvwOe2pRhGVGMhA3F6OQEREJKsIwcwxwqhyL+hMZRvjWAe37iSrUS9YFoN3pKoCUwaT7sFpy5YtKX5v06ZN03AkIiIi6SeIfbaK4B6YeJnGvMtW+O8mdFlo6TmX0wO+6ZJkzzndmsu40n1xuIeHB6ZEEnVioqOj03g0rqXF4SIi2UMIZsrxcbyK4By7Au3nW3rOFcgFPz2RYM85gJ5UZxh1dWvOxTLU4vDXX389xcFJREQko4l7Ow5gO2fjh6bfz0DXhXDllqVR7+qn4IEiDs/Zl1oMoy51KZ3Oo5fUckkBzOxKM04iIllL3NtxM+kEYKnLFPvAZDbqVZkB98pQM04iIiJZQQhmW2gCS0FKW9sUK8OA97fBy/ca9XatBt/bN+qN6xkeUmjKRNwanLZt28aBAwcIDw/Hx8eHhx9+mEaNGrlzSCIiIg4dIyze7Ti70BS3Ue/I+vBBG7tGvY58x1+8TUuFp0zCLcFp+/bt9O/fn+PHjwNgGIZtHVSVKlWYPXs2/v7+7hiaiIiIQ1XwsxWkjCduo96PA2B4fafOG61WKpmKy4PToUOHaNOmDTdv3qR169a0aNGCEiVKEBoaysaNG/n1118JCAhg586dVK9e3dXDExERSZ6QcPtGvQt6QGfHjXod8cREZZLXkkzcx+XB6a233iIqKorVq1fTtm1bu33jx49nzZo1dO7cmbfeeouFCxe6engiIiJ2rE/RXSYi/mxT7Ea9xfLCz0/Bo44b9VpnqzwwYWColUom5fLgtGnTJnr27BkvNFm1bduWnj17smHDBhePTERExF7sp+jiFdaJ3ai3ehFLuYEEGvX2ojofEcBxwmyzS9Z/VmjKXFwenMxmMxUqVEj0mAoVKmA2m100IhERkfjiPkVnN9s0cy88vyrJRr0V8GURvWz1mWKHJAWmzMnlwalkyZLs3Lkz0WN27dpFyZKOpzpFRERcwdFTdPEa9fatBTM7JdiodzgNKEH+dB6puFLiz0img86dO7Np0yZee+01bt++bbfv9u3bTJo0iY0bN9KlSxdXD01ERASwzDYt4m/7jbfvQu+l90PTW81hdpcEQxPAaNZSjo8JYl/6DVZcyuWVw69cuUL9+vUJDg6mUKFC1KtXj2LFinHx4kX27NnD5cuXqVixIrt378bPL3M/ZaDK4SIimU8Q++JXAo/bqDeoM/Sp5fQ5VR08Y8vQlcMLFSrEzp07GTduHAsXLmT16tW2fbly5aJ///689957mT40iYhI5hOCOX5oSmajXke1nlSrKetwa6+6O3fucOTIEVvl8GrVqpEzZ8Jl6TMbzTiJiGQeIZgZw1oW88/9jdvOWGaanGjUC/ASDXmc6jQgyG59lGacMrYMPeMUW86cOalZs6Y7hyAiItmUtT5TFfxYywmeY4X9AYv+hr7LIDIa6paElU8m2KjXBOziOdvTczPpxGBWEo2hWk1ZjJr8iohIthO7PpMHJvun55LZqNcDmElnW2gCCKQ2AVRSraYsyOVP1QH8/vvvdO3alQoVKuDt7Y2np2e8nxw50jfTffHFFzz00EP4+Pjg4+ODv78/v/zyi23/7du3GTZsGIUKFSJfvnz06NGDixcvpuuYREQk/cWtz2QXmu7GwJCf74emkfVhaS+HocmE5dbcaUYRSO14+0vjS3MqKDRlMS6fcfr222/p168fhmFQsWJF6tWrl+4hyZHSpUszZcoUqlSpgmEYzJ07ly5durB//34efPBBRo0axapVq1iyZAm+vr688MILdO/enW3btrl8rCIiknZWcjR+fSaA65GWSuBrjltS0cdt4cX4jXqfoSadqYo/ZRSKsiGXLw7/v//7P8LCwli9ejX16tVz5aWT5Ofnx9SpU+nZsydFihRh/vz59OzZE4AjR47wwAMPsGPHDho0aODw/ZGRkURGRtpeh4eHU6ZMGS0OFxHJAEIw8xwrWMsJBzvDoeN8+DPxRr1PU5Pv6OGC0YorJWdxuMtv1Z09e5bevXtnqNAUHR3NwoULiYiIwN/fn71793Lnzh1atWplO6ZatWqULVuWHTt2JHieyZMn4+vra/spU6aMK4YvIiJJCGIfZZjmODQdCIX6syyhqVhe2NzPYWgCmEIrh9sl+3B5cCpXrhxRUVGuvqxDBw8eJF++fHh7ezNkyBB++uknqlevTmhoKF5eXhQoUMDu+GLFihEaGprg+SZMmIDZbLb9nD17Np0/gYiIJMW6psmhNcehyWw4f93SqHfnc/Co45ZfU2mtW3Pi+jVOAwcO5MMPPyQsLMztRS6rVq3KgQMHMJvNLF26lL59+7J58+YUn8/b2xtvb+80HKGIiKRE7FID09nleE2Tk416AYZTj5dolM6jlszA5cFpzJgxnDx5kkaNGjFx4kRq1aqV4P3EsmXLputYvLy8qFy5MgB16tRhz549TJ8+nSeeeIKoqCiuXbtmN+t08eJFihcvnq5jEhGR1Em01ABYGvW+sgHeu/ewTxKNegHGKTTJPW6p41S7dm3mz5/Ps88+m+AxJpOJu3fvunBUEBMTQ2RkJHXq1CFnzpxs2LCBHj0siwCPHj3KmTNn8Pf3d+mYRETEeYmWGgBLo96+y2DxIcvrN5vDa03BZEr0vDs4Sy/dphPcEJw++eQTRo4cSc6cOWnRogUlSpRwSzmCCRMm0K5dO8qWLcv169eZP38+mzZtYu3atfj6+hIYGMjo0aPx8/PDx8eH4cOH4+/vn+ATdSIi4n7HCHN8Ww4sjXq7LoRtKWvUKwJuCE7Tpk2jVKlSbN++ndKlSyf9hnRy6dIlnn32WS5cuICvry8PPfQQa9eupXXr1rZxenh40KNHDyIjIwkICODzzz9323hFRCRp+Uig32nsRr2+3pZGvS0qOHVOE+CPnpIWC5fXccqTJw+DBw9m2rRprrysW6jJr4hI2ou98Dv2U26x1zbZSWaj3tis7VQcVQaXrCNDN/mtXLky165dc/VlRUQkC4i78HsmnQikdry1TTaLD8GzPznVqDc2D2AhPVUdXOJxeR2nUaNGsXz5ck6fPu3qS4uISCbmaOH3YFbaZqDiNep973d4YqklNHWpCpv6ORWaAEbTkF7UUGiSeFw+41SpUiWaNWvGo48+ysiRIxMtR9C0aVMXj05ERDIqRwu/ozH4mn0UJy8msOy9GwPDVsHMfZaDRtaHD9qAp3NzBR6YqEtJQjArOEk8Ll/j5OHhgclkwnpZUyKPgEZHR7tqWOlCa5xERNJOCGbKMi2hZ+YsnGzUG9tw6vE5e4i+d/vPwMAAu1uBkrVl6DVOr7/+eqJhSUREJDbrrbgEn5izHRirUW/uHJZGvV2qJXn+z9jDBBpTi2I8wVJbMLPeCgygkmaexMblwemNN95w9SVFRCSTirsYPMHZpj9DocN8OHfd0qh35ZNQt5RT14jB4B22Mpg68c4fjcFxwhScxMYli8PHjRvHjh07XHEpERHJIpKsAm615jg0nm0JTQ8UtjTqTSQ0vU4zh9tnshcP7O+IeGKiMu7tqyoZi0uC00cffUTjxo0pXrw4AwcO5OeffyYyMtIVlxYRkUwq0SrgVjP3Wm7P3YiCFuVhe6ClVlMCTEBdSjrcZwCj8cfzXnjyxMRXdNJsk9hxya26CxcusGLFCpYvX878+fP55ptvyJMnD23atKFLly506NCBQoUKuWIoIiKSSVTBz3GTXojfqPfZWvB14o16wRKOvuUvh/s8gBHUZwT1OU4YleMU2BQBNzxVd+vWLdasWcPy5ctZtWoVV65cIUeOHDRs2JCuXbvSuXNnKlas6MohpRs9VSci4hxH1cBDMPM2W/iavcRgCTYxkOJGvVYmwOQgkL1Pa8bSKE0+j2Quyfl97fLgFFtMTAy///47y5YtY8WKFZw8eRKTyUT16tXp1q0bnTt35tFHH3XX8FJNwUlEJGmOqoEDDGRF/LmmuI16Z3W2zDYl00s0ZBo7bCUI3qMVLyk0ZVuZJjjFdejQIZYtW8by5cvZu3cvACVLluTs2bNuHlnKKDiJiCQuBDPl+Nhu9scDyy21eL+cUtGoNzZPTJxiJIBuyQmQwes4JebBBx/kwQcf5NVXX+X8+fMsX76cFStWuHtYIiKSThwtAI9xdGDsRr3lfGH101A96Ua9X9Ce69xhAuuJxoi34FuBSZIrQ804ZTWacRIRSVgIZrZzlt6xik46FLtR76P3GvUWd67n3Es0ZCptCMGs2SVJUIaacdqyZUuK36tedSIiWVPsdU0JLuk2DJi6Hcavt7zuUhW+7w55vZy+zkdsZwT1KY2vApOkiXQPTs2bN09xi5XM3qtORETii1vY0uFs090YeGE1fGVZ78qI+vBhwo16bQ1+44gBVf6WNJXuwUm96UREJLbp7Eq8sGXcRr3TAmBEg0TP+R6tbeuYYlPlb0lrWuOUjrTGSUTEXghmyjIt4dh0LtzScy4ZjXpNwBlGAZZQ9hHbieF+5e9AaqflR5AsKEOtcRIRkewtdnHLY4SleaNeA1jCIXrxIFNpo8rfkq4UnEREJN3ELW75Hq0cr0daexx6LrH0nHugsKXcQCI95+Iaza+8xDpm3pthUmCS9OKWW3XXr1/n008/Zf369Zw/f95hw1+TycSJEydcPbQ0pVt1IpKdOSpu6YmJ3tTgew7eP3DmXnh+FUQblka9PzwOBXOn6JrW4pYKTpIcGfpW3eXLl2nYsCEnTpzAx8fHNtioqChu3boFWKqF58yZ09VDExGRNOSouGU0xv3QFGPAqxtgSvIa9Vo5mrmKxtBTdJKuHD/XmY7eeOMNTpw4wbx587h69SoAo0aNIiIigl27dlGvXj3Kly/PoUOHXD00ERFJQ1XwwyOhKk2378JTP9wPTW80gzldnA5N4Lj8gJ6ik/Tm8uC0evVqHnvsMZ555pl4ZQrq1q3LL7/8wqlTp3jzzTddPTQREUlDpfHlPVrFD0//3YRW82DRIUuj3jldYFJzcLJ0TUJhzAPs2qmIpAeXB6cLFy7wyCOP2F57enrabtEBFCxYkHbt2rF48WJXD01ERNJQEPsYz3r723XHw6BhEGw7a2nUu+YZ6Puw0+e0LjCPG548MLGT51R6QNKdy9c4+fr6cufOHdvrggULEhISYneMj48PFy9edPXQREQkjewhxK46OADbz0LnBclu1GvlAewkkLqUpiC5GcxKu8a9dSmd9h9EJA6XB6eKFSty6tQp2+tHHnmEdevWceXKFQoVKsStW7dYuXIlZcuWdfXQREQkDQSxj4GssF+DtOQQ9ElZo14gXjgKpDYBVFK9JnE5l9+qa9OmDRs2bODmzZsADB48mEuXLlGrVi169epFjRo1OHHiBP369XP10EREJJWsfehsockw4P1tlhYqkdGWRr2b+iYrNE0jgFOMjHcbrjS+NKeCQpO4lMuD05AhQ/j6669twal79+5MnTqViIgIfvjhB0JDQxk9ejRjx4519dBERCSV7EoQ3I2x1Gcav97yekR9S42mvF5On88D6El1hSPJMDJMr7ro6Gj+++8/ihYtmmWaAqsApohkJ3sI4Sv+IIgDlka9TyyFX5xr1OuJiRiMeCUG3qc1Y2mUnsMWydgFMBPi6elJsWLF3D0MERFJgcdZzBL+sbxIZqNeD0w8w0PM40/bNhOW0PSSQpNkMC6/Vbdt2zZGjx5NaGiow/0XLlxg9OjR7Ny508UjExGRhIRgZiPBhGCOt+9VNtwPTX9dhPqzLKGpaF7Y3C/R0AQwgvp8y192s00moDc10mz8ImnF5cHpo48+YuXKlRQvXtzh/hIlSvDzzz8zbdo0F49MREQcCWIf5fiYlsylHB8TxD7bvj2E8C5bLS/WHofG38C565ZGvbueg7qlkjx/FfzitWaJAY4TlpYfQyRNuDw47dmzh8aNGyd6TNOmTTXjJCKSAVifkrMGmxgMBrOSEMwEsY/6zLIc+PVey+2561HQvDxsGwDlCyR5/r7UohNV4xW0VOsUyahcHpwuXbpEqVKJ/xdI8eLFuXTpkotGJCIiCUmoUe/PHOU5VmDEGDBhPQz6GaIN6PMQrH0GCuZO8JwemHiCB9nNc8yhG6XxZSad8LwXnqw1m/QknWRELl8cXqBAAc6cOZPoMadPnyZfPudrfIiISPqwNuqNHZ5MwPOstjTq7bfM0nMOLI16X2+WaM+5l2jICOrHC0UqaCmZhctnnBo0aMBPP/3E2bNnHe4/c+YMy5Yto2HDhi4emYiIxBV3NgjAAIwrsRr15nC+Ue80diR6LRW0lIzO5cFp9OjR3Lx5k0aNGjFv3jwuXLgAWJ6mmzt3Lo0aNeLWrVuMGTPG1UMTEREHAqnNw8R6oOd4GPjHatS71vlGvdEYWvQtmZrLb9U1bdqUjz76iDFjxtC/f38ATCYT1jqcHh4eTJ8+naZNm7p6aCIi4sDPHGUvlv/ITW2jXi36lszOLQUwR4wYQYsWLfjyyy/Zs2cPZrOZAgUKUK9ePYYMGUKNGqrdISKSUSzm3hqmVDbq9dCib8kC3FY5/KGHHuLzzz931+VFRCQJIZjZzlkijTswddv9nnOdq8L87snqORdAJWbRWaFJMj2XB6ft27c7tfB72rRpjBo1ygUjEhGRuKayjXGsszTqHb4avtxr2fFiPfgoADwTXiL7Kk1oRUVuEMVxwmhEGepS2kUjF0lfLm/yW6hQIX7//XceeOCBBI/5+OOPGTNmDNHR0S4cWdpTk18RySz2EMJWztCEsmzmNGNZl+xGvWB54ug0ozSzJJlKhm7ymzt3btq2bcv27dsdFsKcMWMGo0ePVjkCEREX6cdPzI3VYBewNOrtuAAOhFoa9c7vAV0T7zkHllYpOzhLLwUnyaJcXo5gzZo1hIeH06ZNG8LC7B9J/eSTTxg5ciQNGjRgzZo1rh6aiEi2EoKZL9gdPzRZG/UeCL3fqNeJ0GTVmx/s+tmJZCUuD041atRg5cqVnDp1io4dO3Lr1i0APv30U0aMGEG9evVYu3ZtulcOnzx5MnXr1iV//vwULVqUrl27cvToUbtjbt++zbBhwyhUqBD58uWjR48eXLx4MV3HJSLiCtbGvc+z2n5H3Ea9OwOdatQbW+x+diJZjcuDE0Djxo1ZsGABe/bsoWfPnkyfPp0XX3yRRx99lLVr15I/f/50H8PmzZsZNmwYO3fuZN26ddy5c4c2bdoQERFhO2bUqFGsXLmSJUuWsHnzZs6fP0/37t3TfWwiIukpbuNeG0eNeisUTNE1VOhSsiqXLw6PLSgoiIEDB2IymahduzYbNmxw2yLqy5cvU7RoUTZv3kzTpk0xm80UKVKE+fPn07NnTwCOHDnCAw88wI4dO2jQIP4CycjISCIjI22vw8PDKVOmjBaHi0iGspFgWjL3/oYYAyb+BpN/t7zu8xDM6gxenim+hgk4o0XikklkqMXhW7ZsSXBflSpV6Ny5M7///jsTJ07kwIEDdvtdWT3cbLZMKfv5WSra7t27lzt37tCqVSvbMdWqVaNs2bIJBqfJkyfz5ptvumbAIiIpZNe49/Zd6L8cFv5t2TmpmeUnkZ5zJog7VxWP2/6LXCSdpXtwat68OaYkmj4ahuHwFpiryhHExMQwcuRIGjVqZKtaHhoaipeXFwUKFLA7tlixYoSGhjo8z4QJExg9erTttXXGSUQkoxlIbb66shW6LoLfz1ga9c7q5FTPuc9pz/OsTjIcHSdMM06S5aR7cHr99deTDE7uNmzYMP7++29+//33VJ3H29sbb2/vNBqViEjaC2IfA1mBcTwM2n8Px8IsjXp/fAJaVkjy/R5AR6qSkxwMZiXRCcQn9aSTrCrdg9Mbb7yR3pdIlRdeeIGff/6ZLVu2ULr0/cq2xYsXJyoqimvXrtnNOl28eJHixYs7OJOISMYTgpljhFHlXoh5jhWw4yx0Xgj/3YSyvrD6KXiwqFPnm0JrSuNLILUJoBLHCaMyfizgb15mHTFYQpN60klW5bZede5mGAbDhw/np59+YtOmTVSoYP9fWnXq1CFnzpxs2LCBHj16AHD06FHOnDmDv7+/O4YsIpIsQeyzPT1nAsrim6xGvbHXMnlg4j1a8RKNbPtL42sLR2NpxJPUsAUphSbJqtI9OEVERJA3b163nyOuYcOGMX/+fJYvX07+/Plt65Z8fX3JnTs3vr6+BAYGMnr0aPz8/PDx8WH48OH4+/s7XBguIpKRxC05YBgGpz9YDeOcb9RrAIvpSRHyOhWGYgcpkawq3es4VahQgalTp9rVR3LWjh07aNu2LR999FGaj+uLL77AbDbTvHlzSpQoYftZtGiR7Zhp06bRsWNHevToQdOmTSlevDg//vhjmo9FRCQthWBmJnvv12m6GwPPr7ofmobXgx8fTzQ0gWWWyZ8yNKeCApHIPelex2nkyJF88cUXeHl50b17d3r27EmDBg0oUqRIvGPv3r3Ln3/+ybp16/j+++/5559/qF69OrNnz+bRRx9Nz2GmCzX5FRFXiL2OaS0nLIu/rTuvR0LvH2D1Macb9YLl0K/pTCC103HkIhlDcn5fu6QA5rFjx/jf//7HkiVLiIqKAqBUqVIUK1aMAgUKcPv2bcLCwggODiYyMhLDMKhevTqjR4+mX79+eHi4pcB5qik4iUh6sz0lhyXsQKwaSils1NuKCrzLY9SldJLHimQFGS44WYWFhTF//nw2bNjA9u3buXz5sm1fzpw5qVGjBs2aNaNbt240adLEVcNKNwpOIpKeQjBTlmmOCwL8ddHSPiUk3NKod+WTUC/pnnPWwpgemJhJJ804SbaQYYNTXHfu3OHKlSu2xdhZjYKTiKSnxfzNEyyNv+PXE9BzsaXnXLXClnIDKeg554mJU4zU+ibJ8jJUy5XE5MyZUzWRRETS0qx9MORniDYsjXp/fBwK5k7RqayNehWcRO7LnIuHRESyuRDMXOHm/Q0xBry6AQautISmZx6CNU+nODRZ7eF8KkcqkrUoOImIZDJB7KMs03ie1ZYNt+/C0z/Cu/faRr3eFOZ1Be+Ebyq8QD08sG+H5ag51gTWE4I5bQYukgUoOImIZCLWwpa2xalXbkLrb2Hh35ZGvXO6wJstIIkeoU0py0w64XkvLnliYgwN4x1nvV0nIhbZtuWKiEhmYq3VdJmI+4UtT4RBu1iNen94HB6r6PQ54/abA/iIHffPj5r1isSl4CQiksHFrtVkk4pGvQD+lAHit0mZSScGs5JoDDXrFXFAwUlEJAMLwRw/NC39B5750dKot04J+PmpBBv1OvISDRMMQ3FnoRSaROy5fI3Trl27XH1JEZFMydpzzhaaDAM+2A69llhCU6f/g839khWaPIAR1E/0mNL4qj+dSAJcHpz8/f2pVasWn376KdeuXXP15UVEMoWpbKMs0/gfWywb7sbAsNUwdp3l9fB68NMTSTbqfZDCtn/Re2JiJp0ViERSweWVw5999ll++OEHbt26Ra5cuejZsycDBw7MEi1W4lLlcBFJiQ/YxljW3d9wIwqeWHq/Ue9HATAy8Ua9AVTkf7SkLqUJwaxbbyKJyPAtV8xmM9999x1BQUEcOHAAk8lElSpVGDhwIH379qVw4cKuHlK6UHASkeQIwcx2ztq3UYnbqPf77tDtgSTPtZvn1KRXxEkZPjjFtm/fPr7++msWLlyI2WzGy8uLLl26MHDgQFq1auXOoaWagpOIOCuIfQxipV0pgJQ26u1LLebQzfbaWsqgimacRBzKVMHJ6tatWyxZsoRXXnmFCxcuAFCuXDmGDBnC0KFDyZ8/v5tHmHwKTiLijBDMlONj+9CUwka9Hpg4Hasxb+xA5oGJmXQikNrp9VFEMqXk/L7OEJXDr169ysyZM5k6dSrnz1v6IjVq1Ijr16/z8ssvU7VqVfbs2ePmUYqIpI/tnLUPTbP2QfvvLaGpeXnYPsCp0AQQE6vSt7XKuPXcMRgMZqVaqIikgluD08aNG3nqqacoVaoUo0aN4tKlS4wdO5Zjx46xZcsWQkJC+Oyzz7h+/TrDhw9351BFRNJcCGbG8uv9NU1p1Kg3LzkBOEaYfSBDLVREUsvlBTAvXrzI7NmzCQoK4uTJkxiGQbNmzRgyZAjdu3cnZ86ctmO9vb0ZOnQox48f57PPPnP1UEVE0k28NU2Rd6H/cljwt+X1603hjeZJ9pxzJII7AFTBDw9MaqEikoZcHpxKly5NTEwMBQsWZOTIkQwaNIiqVasm+p4iRYoQFRXlohGKiKSvuLfQuHITui2CrWcsjXq/7gT9Hk7RuWMHo9L4qoWKSBpz+eLwxo0bM2TIEHr16oW3t7crL+1yWhwuInGFYGYxhxjDr5YNqWzUa7r3EwO2YBR38bfqOIkkLjm/r10+4/T777+7+pIiIhlCvNtzKWjUa71xZ3A/KCXVWy5uI18RSTk1+RURcYF4t+eW/gN9foLbdy2Nelc+CSWSLrtivUXggYkptLLNLikYibiGy4NTy5YtkzzGw8MDHx8fqlatSteuXalfP/GGlCIiGd10dllCk2HAhzvu95zr9H+woEeSPefiisHgZdbTmxoKTSIu5PI1Th4elgoIJpMJR5eOu91kMtG/f39mzZrlsjGmFa1xEhGwzDaVYZqlUe+Lv8AXf1h2vFAXPm4LnglXhulOVZbzL9E4/lf1RvrSnArpMWyRbCNDF8C8desWnTp14oEHHmD+/PmcPn2a27dvc/r0aebPn8+DDz5I586dOXv2LL/++iu1a9dm9uzZfPHFF64eqohImpjOLkuj3i4LLaHJBEwLgBntEg1NJmA67TnFSBbTEw/sSxOotICI67l8xunll19m8eLFHDx4kLx588bbHxERQc2aNXn88ceZMmUK165do1q1apQtW5bdu3e7cqipphknEfmZo3Q6PxM6zof9zjfq9QBm0tnuCbkg9sUrLaD2KSKpl6FnnObPn0/37t0dhiaAvHnz0r17dxYsWABAgQIFaNu2LYcPH3blMEVEUq0fP9Hp4MdQf5YlNBXJAxv7JhmaAIc35gKpzSlGspG+nGKkQpOIG7h8cfjly5e5c+dOosfcvXuXS5cu2V6XKFGC6Ojo9B6aiEia2EMIH7KdRb+utG/Uu+opqOhczzkDGMxKAqhkt/hbpQVE3MvlM06VKlViyZIlXLlyxeH+K1eusHjxYipVqmTbdv78efz8dB9fRDK+fvxEPWaxKOi7+416m5WzNOp1MjRZqa+cSMbj8uA0fPhwQkNDqV27NjNmzGDv3r2cPXuWvXv3MmPGDGrXrs3FixdtTX1jYmL47bffqFu3rquHKiLilBDMbCSYOexnrnEAJv4Gz8Vq1Lv2mWQ36gUt/hbJiFx+q27w4MGcO3eOyZMnM2rUKLt9hmHg4eHBhAkTGDx4MABhYWG89NJLNGzY0NVDFRFJkl018LiNel9rCm82T1GjXoBuPKDbciIZjMufqrM6duwY8+fP56+//iI8PBwfHx9q1apF7969+b//+z93DCnN6ak6kawtBDNlmWZZyJ2GjXpjm0prXqJRqs8jIglLzu9rlwenefPmUaxYMQICAlx5WbdQcBLJ2p7hB77noKVRb/v58O8V8PGGH5PXqDcxHpg4zUjNPImkowxdjiAwMJA1a9a4+rIiImmqF4stoWnHWWgQZAlNZX1h2wCnQ5MJGEIdFtOTlTzp8JgYLRAXyVBcvsapRIkS3L1719WXFRFJM3sIYSn/wA//wDP3GvXWLgE/O9eoF+AZajKZVnYzSe/TmnGssztOC8RFMhaXzzh17tyZdevWERkZ6epLi4ikiaHGz/Dhdui1xBKaOv4fbO7ndGgCSzHLuLffxtKIqbS2tVaxVgfXbTqRjMPla5zMZjMtW7akePHivP/++zz44IOuvLxLaY2TSNayhxA63f2eiy8uTVaj3riSWrcUgpnjhFEZP4UmERdIzu9rl9+qe+SRR4iMjOTAgQOsWbOGXLlyUbRoUUxxHtc1mUycOHHC1cMTEXGoHz8x98YeeGIprD5mWaD0UQCMqJ/scgPvxblFF5eqg4tkXC4PTjExMXh5eVG2bFm77XEnvtxUJUFEJJ6fOcrc87/fb9Sb616j3u5J95yLzQOYovICIpmay4PTqVOnXH1JEZEUCcHMdHbxwcGfoMN8OBtuadS78kmoX9rp83gAC+mJP2U0kySSybk8OImIZAYfsI1xrMNYdwJ63GvUW7UQrH46WT3nTMBMOtOLGuk3WBFxGbcGp3/++YcjR44QERFBnz593DkUERGbqfdCE9/sh8E/w90YS6PeH58AP+d6zrWlEgN4RLNMIlmMy8sRAOzZs4eHH36YmjVr0qtXL/r162fbt2XLFvLkycOKFSvcMTQRyeZ+5ijjjF8tjXoDV1hCk7VRr5OhCWA8jelFDYUmkSzG5cHp0KFDtGzZkuDgYEaNGkW7du3s9jdp0oTChQuzZMkSVw9NRLKpEMws5m8a8DWdIr+1FLV8Z6tl52tNYV5X8HZ+gl5FK0WyLpcHp0mTJgGwd+9ePvjgA+rWrWu332Qy4e/vz549e9J1HFu2bKFTp06ULFkSk8nEsmXL7PYbhsHrr79OiRIlyJ07N61ateLYsWPpOiYRcb0P2EZZpvEES9kVdhxafwvzD1oa9X7TGd5qkaxyAx6gopUiWZjLg9PmzZvp0aMHlStXTvCYsmXLcuHChXQdR0REBLVq1eKzzz5zuP/9999nxowZfPnll+zatYu8efMSEBDA7du303VcIuIaIZh5hh8YyzoMsDTqbRgEW89YGvWueRr6P5Ls8y6kJ4HUTvPxikjG4PLF4devX6do0aKJHnPr1i2io6PTdRzt2rWLd5vQyjAMPv74YyZOnEiXLl0AmDdvHsWKFWPZsmX07t3b4fsiIyPtWsmEh4en/cBFJNWC2MdAVmCrFrczBDotgP9uWhr1rnoKaiT+7ylHPDHhT5k0HauIZCwun3EqU6YMBw8eTPSYffv2UalSJReNKL7g4GBCQ0Np1aqVbZuvry/169dnx44dCb5v8uTJ+Pr62n7KlNG/QEUymj2E2IemH/6BFnMtoal2CdgZmOLQpFt0Ilmfy4NTx44d+fXXX1m/fr3D/YsXL2bnzp107drVtQOLJTQ0FIBixYrZbS9WrJhtnyMTJkzAbDbbfs6ePZuu4xSR5AliH/WZZQlNhpHqRr1Wi+nJKUbqFp1INuDyW3WvvPIKS5cupX379vTt29cWRD7//HN27NjBggULKF++PKNHj3b10FLN29sbb29vdw9DRGIJwcwxwshHTgax0hKa7sbAiF/g83uNeofVhenJa9QLluKWX6u4pUi24vLgVKRIETZv3kyfPn0ICgqybX/hhRcAqF+/PgsWLMDX133T3cWLFwfg4sWLlChRwrb94sWLPPzww24alYgkVxD7GMRKYjDwwEQMBtyIgt5LYdW9Rr0ftoGRDZx6cs7aa678vdtxKm4pkv24pXJ4xYoV2bZtGwcOHGDnzp2EhYXh4+ND/fr145UncIcKFSpQvHhxNmzYYAtK4eHh7Nq1i6FDh7p3cCLilBDMttAEWP73/PUUNer1wMRo/BlBfQUlkWzOrS1XHn74YbfN4Ny4cYPjx4/bXgcHB3PgwAH8/PwoW7YsI0eO5O2336ZKlSpUqFCB1157jZIlS7p17ZWIOO8YYbbQBMDBiylu1Luc3nSkajqNVEQyk2zb5PePP/6gRYsWttfWNVV9+/Zlzpw5jBs3joiICAYNGsS1a9do3Lgxa9asIVeuXO4asogkw+fsvv9i3QnouQTCI1PUqDcfXra1UlXw06yTSDZmMgzDSPqwtHX58mVmz57Nnj17uHbtmsOaTSaTiQ0bNrh6aGkqPDwcX19fzGYzPj4+7h6OSLYxh/30Z7nlRSoa9Vo9TU0W8LdtrdRMOukJOpEsJDm/r10+4/TXX3/RsmVLrl69SmKZzZSMFgciIlYd+J7VHLOUG3ht4/2ec0/XhKDOyeo5Z/U992vPxWAwmJUEUEkzTyLZkMvrOI0ZM4awsDBeffVVgoODuXPnDjExMfF+0rtyuIhkPR2toSnybvxGvd92S1FociQag+OEpcm5RCRzcfmM044dO+jatStvvfWWqy8tIlnYHkJYxTEIuwVdF1p6zuXwgJkdk91zzgOISWS/JyYq45eq8YpI5uTy4OTl5eXWdioikjVt5QycvArtv4ejVyyNen94HFpVTNZ5PDGxg0BOcY3e/GD/ZB5qrSKS3bk8ODVr1ow//vjD1ZcVkUzK2afZCuz8DzrPgss3oYyP5cm5ZPacs4aiupSmLqUJJ4rBrCQaAw9gNA1Vy0kkm3P5U3UnTpygQYMGjB8/npdeesmVl3Y5PVUnkjpxK38n9DTbDz/8wNPPPE3k7UhLo96fn0x2z7lpBNCT6vFCUQhmjhNGZZUhEMmykvP72uXBacCAAQQHB7NlyxYqVKjAww8/7HCQJpPJriVLZqTgJJJyIZgpx8d2t8o8MXGKkbYAYxgG06ZN46WXXrI8pduhCizsCfm8knWtuOcVkewlQ5cjmDNnju2fT548ycmTJx0elxWCk4ikXLzK39x/mq00vty9e5cnRwSy9PN5lp3D6sLHbS0LwpNBa5ZEJDlcHpyCg4NdfUkRyYSq4He/Me89HsBhLnP5xlUCe/fl+qq/k92oN7ZJNOU56ig0iYjT3FI5PLvQrTqR1Im9xskmhY164zIBZxil0CQiGftWnYiIsx6iaOKNelc8CQ2ca9Qbmwcwk84KTSKSbC6pHN6yZUvmzZtnt23Xrl3MmDHD4fHvvfcehQoVcsXQRCSDCmIfDYi1znH9SWg82xKaqhaCnc8lOzR5AIvpyWlGqdeciKSIS4LTpk2bOHXqlN22NWvWMGrUKIfH3759m2vXrqX/wEQkQwjBzEaCCcFse213i+6b/dDuewiPhKblYHsgVCyYrGt4YmImnelFDc00iUiK6VadiLiVo1pNFSloCU2GAa9vhLfv9Zx7qiZ8k/xGvQnVaBIRSS6XN/kVEbGKO7MUg8FgVhJB1P1GvdbQNLEJfJf8Rr0eoNAkImlGM04i4jYJ1Wr6JGwTdPsOtpy21GX6qiMMSF6jXrA8OadF4CKSlhScRMRt8pEz/saTV/m1/aepatQL8AXt6UhVhSYRSVMKTiLiNje4Y79hZwh0XpAmjXr11JyIpAeXBaeff/6Z0NBQ2+s//vgDgOeffz7esXv27HHVsETEjargd//Fj4fh6R/h9l1Lo96VT0LJpBv1emBiIT0oTwEiuKNmvCKSrlxSOdzDI/lr0E0mE9HR0ekwGtdR5XAReyGYOUYYVfDjAtcZxVq2GWdg2k546VcwSFGj3o30pTkV0m/gIpKlZbjK4Rs3bnTFZUQkA4tddsCEJSNxNwZGroHP7s0yP/8oTG+XrEa9npioHHvmSkQkHbkkODVr1swVlxGRDCpu2QED4EYUPPkD/Pyv5fG3D9rAqOQ16rWuZ9KtORFxFS0OF5F0F6/swIXr0HEB7LuQoka9HsBCeuJPGYUmEXEpBScRSXd2ZQf+vgTtv09Vo94YoAh5FZpExOUUnEQk3VgXgy/ib8uG9Sehx2JLz7mqhSzlBpLZcw60rklE3EfBSUTSRezF4ADM3g+DfrYsCG9aDn56AvxyJ/u8WtckIu6k4CQiaS4EMwNZYYlMadSoV+uaRCQjUHASkTT3DD9aQlPkXQhcAd8ftOyY2ATeauH0k3PWsgXWWaZe1EinEYuIOEfBSURSLXZhyy/4g82chrBb0G1Rihv1moBdPKdq4CKSoSg4iUiqOCxsefKq5ck5a6Pepb2gdaVknfd9WlOX5D1tJyKS3tI9OFWsmPyu5mBpuXLixIk0Ho2IpCWHhS13hUCnWI16Vz0FNYsl67yv0oSXaJT2AxYRSaV0D04xMTGY4qxniIqK4sKFC5YB5MhBoUKFuHLlCnfv3gWgRIkSeHk536dKRNzjGX60L2yZwka9sb1CE97msTQeqYhI2kh+991kOnXqFMHBwbaf/fv3U6JECZo2bcrWrVu5ffs2Fy5c4Pbt22zZsoWmTZtSsmRJDhw4kN5DE5FUeJUNlrVMYHlybtoO6LnYEpo6VIHN/ZIdml6lCe8oNIlIBpbuwSmu8ePHc/v2bTZs2ECjRo3w8LAMwcPDg8aNG7N+/Xpu3rzJ+PHjXT00EXFSCGbe5V55gbsxMPwXGP2r5V7d84/Cst6QL/mzxq1I2a19ERFXcXlwWr58OR07dsTT09Ph/hw5ctCxY0eWL1/u4pGJiLPeZovlH25EWZ6c+2yP5TG4D9vAp+0tT9ElkweoGriIZHguf6ouPDwcs9mc6DFmsznJY0TEPYazmq/YG79R73fdoEf1FJ93Cq1VckBEMjyXzzg9+OCDLFy4MMEn5o4dO8bChQupUUOF7kQymsdZzKfstjTqbRBkCU1F8sDGvikOTR6YmEprxuopOhHJBFw+4zRx4kS6devGI488QmBgII0bN6Zo0aJcunSJrVu38s033xAREcHEiRNdPTQRSUAIZlZylCX8Y9+o9/8KweqnoFLKbrEtVgsVEclkTIZhGEkflrbmzZvH8OHDuX79ul2pAsMw8PHxYcaMGTz77LOuHlaaCw8Px9fXF7PZjI+Pj7uHI+KU2FXAS+PLRDbwLlstRQdiN+ptUtayCNzJRr0v0ZCP2E4MlqnumXQmkNrp+ElERJyTnN/XbglOANevX2fZsmX8+eefmM1mfH19qVWrFl26dMkyIUPBSTKb2FXAPTDxCMXZy4VUN+r1AE4zCoDjhKmFiohkKJkiOGUHCk6SmYRgpizTiPcvhFQ26gVL+xStYRKRjCo5v6/d2qvuxo0b/Pvvv0RERNCkSRN3DkUk25vOrvih6eq9Rr2bT4OnydKoNzD5t9deZj1+5NatORHJ9Fz+VB1Yqol36dKFggULUrduXVq0aGHbt23bNqpXr86mTZvcMTSRbCkEMx+xw37jyavgH2QJTT7e8MvTKQpNADEYDGYlIajMiIhkbi4PTmfOnKFBgwasXr2aLl264O/vT+y7hfXr1+e///5jwYIFrh6aSLYRgpmNBNuCzDHC7HvO7QqBBrPg6BVLo97f+0PrSqm6ZjQGxwlL1TlERNzN5cFp0qRJXL16lc2bN7N06VJat25ttz9Hjhw0adKEbdu2uXpoItlCEPsox8e0ZC7l+Jgg9lEFP2wrln46DM3nwuWb8Ehx2Pkc1CyW6ut6YlJlcBHJ9FwenNauXUu3bt1o2LBhgseUK1eOc+fOuXBUifvss88oX748uXLlon79+uzevdvdQxJJkRDMtqfm4P4tNIA2RkVLo94esRr1bumf7Ea9jnhi4is66Uk6Ecn0XB6cwsLCKF++fKLHGIZBZGSkawaUhEWLFjF69GgmTZrEvn37qFWrFgEBAVy6dMndQxNJtni35LDcQmsTPZe1L356v1Hv0JQ36o1rGgGcYqQWhotIluDy4FSsWDGOHTuW6DEHDx6kbNmyLhpR4j766CMGDhxI//79qV69Ol9++SV58uThm2++iXdsZGQk4eHhdj8iGUkV/PAgThmBiCgOd/sMPt1jef1Ba/gsZY164/LERE+qa6ZJRLIMlwen1q1b8/PPP/PXX3853L9161Z+++032rdv7+KRxRcVFcXevXtp1aqVbZuHhwetWrVix44d8Y6fPHkyvr6+tp8yZcq4crgiSSqNLzPphKc1PF24Ds3mwMp/LY16l/SCMQ2TVaMJLAFpFp15n9a2f6no9pyIZEUuL4B56tQpHn74YQDGjh3LkSNHmD9/Pj///DPbt2/no48+Im/evPz555+UKFHClUOL5/z585QqVYrt27fj7+9v2z5u3Dg2b97Mrl277I6PjIy0u8UYHh5OmTJlVABTMpwQzPQ59BWb2r8LZ8xQOA+sfBIalHbq/f+HH//ee0LOAxPv0YqX7hW4DMGs6uAikqlk6AKY5cuXZ+3atfTu3ZvXXnsNk8mEYRh07NgRwzAoW7YsS5cudXtoSglvb2+8vb3dPQyRBIVgZjtn2bZhM1u6T4Lw28lu1DuU2nzFftvrGAxeZj29qUFpfG0/IiJZkVsqh9evX59jx46xcuVKdu3aRVhYGD4+PtSvX58uXbrg5ZX6BalpoXDhwnh6enLx4kW77RcvXqR48eJuGpVI8lib9u7lPONYhzHnAAxceb9R709PQKE8Tp+vCPkcLjA/TpgCk4hkeW5ruZIjRw66detGt27d3DWEJHl5eVGnTh02bNhA165dAYiJiWHDhg288MIL7h2cSBJCMDOdXXzIdkvMMQyYtAn+t8VywJM1YHYXpxv1guW2XEf+j7fZaheeVKNJRLILly8Ob9myJfPmzUv0mO+++46WLVu6aESJGz16NF9//TVz587l8OHDDB06lIiICPr37+/uoYkkKIh9lGUaH1hDU+RdeHbZ/dD0ahP4rrtTocn6FJ51LVNdStstMNcicBHJTlw+47Rp0yaaN2+e6DGnT59m8+bNrhlQEp544gkuX77M66+/TmhoKA8//DBr1qyhWLHUV1IWSQ8hmBnIivvzQals1PsUNfieg8RgMJ71FLzXrDeASloELiLZjttu1SUmIiKCnDlzunsYNi+88IJuzUmGZF2/VCVWeNnO2fuhKfgqtJ8PR/6D/F6w9HFok7yec99z0HY+a6XxACppEbiIZEsuCU5nzpyxe33t2rV42wCio6M5e/YsP/zwQ5LVxUWyuyD22dqneGBiJp0IpDYbCLYcsPscdFoAlyIsjXpXPZXsnnMmIG69Ei0EF5HszCV1nDw8PDAlo6CeYRhMnTqVMWPGpOOo0l9y6kKIJEcIZsrxcbwF2jsIpB6zLI16n/4Rbt21NOr9+alk95zzwMQUWvEy6+Nd5xQjFZxEJMvIcHWcnn32WVu9pnnz5lGrVi1bEczYPD098fPzo2XLlrRt29YVQxPJlBLqObfSOAof74Ax93rOta8Ci3qmqOfccnrTkar4kZvBrCQaQwvBRSTbc0lwmjNnju2fN2/eTP/+/XnxxRddcWmRLMnac84uPEXHMG/kFPh0veX10EdhRrsU95zLhyVsaSG4iMh9Ll8cHhwc7OpLimQ51p5z1pkgIqLgyR84vfJfywEftIbR/snuOWcVty6TFoKLiFi4vI7TP//8w4wZM7h8+bLD/ZcuXWLGjBkcPnzYxSMTyVwCqc3z1E2zRr1Wuh0nIpIwlzf5ffbZZ9mwYQNnz57FwyN+bouOjqZ8+fK0atWK2bNnu3JoaU6LwyWtxS4/sJC/GXvoe0u5AWuj3hW9wb9Mis7tiYkF9MCfMgpNIpKtZLjF4bFt3bqVxx57zGFoAssC8ccee4wtW7a4eGQiGVvs8gMmwNhwErovhvDIZDfqjcsD+IpO9KJGmo5ZRCSrcXlwCg0NpUyZxP+LuFSpUly4cMFFIxLJ+EIw20ITYN+ot3FZWOZ8o16Pe9WZYrDMMo3CnxHU1yyTiIgTXB6c8ubNy6VLlxI95tKlS+TKlctFIxLJ+KazyxKaHDXq/aaLZW2TE6yFMvWUnIhIyrh8cXjt2rVZtmwZ165dc7j/6tWr/PTTT9Su7XwvLZGsIgQzGwkmBLPdtg/ZnnCjXqdDE+wkkEBqUxpfmlNBoUlEJJlcHpyGDRvGlStXaNGiRbx1TJs3b6ZFixZcvXpVveEk2wliH+X4mJbMpRwfE8Q+4F7vuau3oO338N1flka9X3eCt1uCh3NPznliYiadqUvp9PwIIiJZnsufqgMYM2YM06ZNw2Qy4e3tTfHixQkNDSUyMhLDMBg7dizvvfeeq4eV5vRUnTgroRYqU2jF2ODFKW7UawIW0VNPyomIJCI5v69dPuME8OGHH7JixQoCAgLImzcvISEh5MuXj3bt2rFq1aosEZpEnBWCmcUccthCZezuOdAgyBKaSvvAtgFOhyaAZ6lFL2ooNImIpBG3zDhlF5pxkqTELjEQT+xGvQ8Xh1XxG/W2pgLrCXb0bkANeUVEnJHhZ5xEJH6JARvDgI93Qo/FltDUvgps6RcvNJmAb+jKCp5M8BrRGBwnLO0HLyKSTSk4ibjJds7GD03RMTBiDYxaCwYwpA4s7w35veO93wCOE0ZHqtKXWg6vEbfnnIiIpE66BycPDw9y5MjBv//+a3vt6emZ5E+OHC4vMSXiMkHsozdL7TdGREG3RfDJbsvrqa3h8w6Qw/H/TT3AForm0I3dPMcTPHivwKV6zomIpId0TydNmzbFZDKRJ08eu9ci2ZX1Fp3dXFPoDeg4H/ZesNRl+rYb9Kye6HkMYC0nCMRS86wupVlILz7ArOKWIiLpRIvD05EWh4sjGwmmJXPvbzh0KcWNerX4W0Qk9TJ0k1+R7CgEM8cIowp+5CPnvW5xwG/B0H0RmCOhih/88nSyGvVaF38rOImIuIaCk0g6i11ywBaYAOYegOdS1qjXSou/RURcK92D04ABA1L0PpPJRFBQUBqPRsS14pYcMMBSbuCNTfDWvZZDvWvAbOca9Q6hDl+zj2gMPO5VFtdsk4iI66T7GicPD8dPBJlMJhxd2rrdZDIRHR2dnkNLd1rjJPHWM0VFw3Mr4Nu/LK9faQz/c67nnAdwmlEs4G/Gsw4D8MDETDrZFoiLiEjyZag1TsHBwXavY2JiGDFiBDt37mTEiBE0adKEYsWKcfHiRbZs2cKMGTPw9/dn2rRp6T00kXRjXdMUQdT9jVdvQffFsOmUpVHvlx3hOecDzxRaA/Ay6223+2IwGMxKAqikmScRERdI9+BUrlw5u9dTpkxh165d/Pnnn5QoUcK2vWrVqjRt2pT+/fvzyCOPsHTpUsaNG5fewxNJE7EXf8eeEbIJvpriRr1guUU3lkZsJNhhTzstEBcRcQ2XLw4PCgri8ccftwtNsZUqVYrHH3+cr7/+WsFJMoVE+80B7D4HnRbApQhLo95VT8FDxZw+vwfwKk0BqIIfHpjsrqUF4iIiruPylishISHkypUr0WNy5cpFSEiIi0YkknIJ9puzWnYEms+xhKaHi8POwGSFJk9MzKSzbTapNL7MpBOeqg4uIuIWLi+AWaVKFQzD4O+//3YYoG7evEnNmjXx8PDg2LFjrhxamtPi8Kwv3uLv2D7eCaPv9ZxrXwUW9nDYc86RL2hPNYokWP07RNXBRUTSTHJ+X7t8xum5557j5MmTNGrUiOXLl3PlyhUArly5wrJly2jcuDGnTp1i4MCBrh6aSLJZb53ZiY6BEb841ajXEU9MdKQqzamQYCgqjW+i+0VEJH24fI3T2LFj+ffff5k9ezbdu3cHLCULYmJiADAMg/79+zN27FhXD00kWawLwttSmdXcmx2NiIKnfoQVRy2v328FLzUEJ/sz6tabiEjG5rZedZs3b2bu3Ln89ddfmM1mfH19qVWrFn369KF58+buGFKa0626rMvhgvDYjXq9PS2Nens9mKzzDqYOX9IpjUcrIiKJSc7vazX5TUcKTllTCGbK8bF9aDp0CTrMh9P3GvUu7w0NnWvUG5ua9oqIuF6GKoApkhXErtO0kqP2oSmVjXpjU00mEZGMzS3B6e7du3zyyScsWLCAI0eOcPPmTe7evQvAgQMHmDlzJiNHjuT//u//3DE8ETuJ1mlyslGvCZhAEwqTm4Lk5hq3qYwfXViomkwiIpmIy4PTrVu3aNOmDdu3b6dw4cL4+PgQERFh21+hQgVmz56Nn58fb7/9tquHJ9lY7Fkl64xPgnWaDAPe3Gz5gSQb9RrAu2wF7veX60hVZtKJwawkGkMLw0VEMgGXlyN499132bZtG5MnTyY0NJTnnnvObr+vry/NmjVj7dq1rh6aZGNB7KMcH9OSuZTjY4LYB8B2zsYPTVHR0HfZ/dD0SmP4vnuCoSkua3+5EMwEUptTjGQjfTnFSDXrFRHJ4Fw+47Ro0SJatGhha6dicvCYdsWKFdm/f7+rhybZVNxZJWuwucotxrHO/uBUNuq1ir2WyfojIiIZn8tnnM6cOcOjjz6a6DH58+fHbDa7aESS3R0jzGHj3LGOGvU2/MYSmvJ7WXrOpSA0WeUlZ4rfKyIi7uHy4JQ/f34uXbqU6DEnTpygSJEiLhqRZHdV8Itb+zu+3eegQRAc+c/SqPf3ARBQOdG3PMGD7OY5PiLA4f4I7qRswCIi4jYuD04NGjRg5cqVXLt2zeH+s2fPsnr1apo2beragUm2E4KZjQRzgNDED0xho94x+FOX0vSiery2LHp6TkQkc3J5cBo7dixXr17lscceY9u2bbYyBDdv3mTDhg0EBARw9+5dRo8e7eqhSTYSezF4JxY4KjRgMX2npUbTrbvQrjJs6QelnCtmeoprbCQYgJl0wvNeeNLTcyIimZdbKod/8cUXjBgxgujo6Hj7PD09+fzzz+M9bZcZqXJ4xuSw8ndc0TEwei3M2G15PaQOfNIecjj33xoemDAwMLhffiCAShwnjMqxyh2IiIj7ZYqWK4cPH+bLL79k165dhIWF4ePjQ/369Xn++ed58MHk9ffKqBScMqaNBNOSuQkfkMpGvdajYv8fS61UREQyrgzdcmXLli34+Pjw8MMPM336dFdfXoR8iT3NFnoDOi2AP86nuFHvZ7TneVbbbVMrFRGRrMHla5xatGjBzJkzXX3ZeN555x0aNmxInjx5KFCggMNjzpw5Q4cOHciTJw9FixZl7NixtjVZkjkFsY/6zHK889AlaDDLEpoK54Hf+iY7NJmARympxeAiIlmUy4NT0aJFyZUrl6svG09UVBS9evVi6NChDvdHR0fToUMHoqKi2L59O3PnzmXOnDm8/vrrLh6ppJb16bk9hDCIlY5XNv0WDI2+gdNmS6PeHYHQsEyyr2VgKTOgxeAiIlmTy9c4Pfvss/z999/s3bvXYdVwV5szZw4jR46MVx7hl19+oWPHjpw/f55ixSyPnn/55ZeMHz+ey5cv4+XlleS5tcbJ/WI36DWB49DkZKNeZ8ReyxSCWYvBRUQygeT8vnb5jNOUKVO4cuUKgwYNIiwszNWXd9qOHTuoWbOmLTQBBAQEEB4ezqFDhxy+JzIykvDwcLsfcZ8QzAxkhe3puXihyTDgjU3Qb7klNPWuAev6JCs0mcB2Wy7uzFJpfGlOBYUmEZEsxOWLw5955hkKFCjAN998w3fffUeFChUoVqxYvNknk8nEhg0bXD08m9DQULvQBNheh4Y6Lpg4efJk3nzzzXQfmyQuBDPbOcu3/JlwwYGoaHhuBXz7l+X1hMbwdkvwcH4WdBJNeY46AJpZEhHJJlwenDZt2mT758jISI4cOcKRI0fiHZeS23gvv/wy7733XqLHHD58mGrVqiX73M6YMGGCXeHO8PBwypRJ/joZSbkg9jGQFYlVaLI06u2xGDaesjTq/aIDDKyT7Gs9SFG72SUREcn6XB6cYmJi0u3cY8aMoV+/fokeU7FiRafOVbx4cXbv3m237eLFi7Z9jnh7e+Pt7e3U+SXt7SGE51iR+EGnrkH77+Hwf5ZGvUt6JdlzzhET4I9CsYhIduPy4JSeihQpkmbNgf39/XnnnXe4dOkSRYsWBWDdunX4+PhQvXr1NLmGpB3rIvBE7TkHHRdYes6Vyg+rnoJajkNwYjyAmXTWLJOISDbkssXhO3bsoGXLluTPnx8fHx9at27Nrl27XHX5eM6cOcOBAwc4c+YM0dHRHDhwgAMHDnDjxg0A2rRpQ/Xq1enTpw9//vkna9euZeLEiQwbNkyzShlMCGbbk3MJWn4Ems2536h313PJCk0m4FWasJG+nGYUgdRO9bhFRCTzcUk5goMHD1K/fn1u375ttz137tzs3r3bLS1W+vXrx9y58dtubNy4kebNmwNw+vRphg4dyqZNm8ibNy99+/ZlypQp5Mjh3ESdyhG4RpItVKbvhFFrLY/VtasMi3pC/uSF3908R11Kp26gIiKSIWW4cgRTpkzh9u3bvPrqq4SGhhIaGsprr73GrVu3klzMnV7mzJmDYRjxfqyhCaBcuXKsXr2amzdvcvnyZT744AOnQ5O4ThX84lXqBiyNekf8AiPvhabBdWDFk8kOTR6YKEH+tBmsiIhkai6ZcSpbtizly5dny5YtdtubNWvGqVOnOH36dHoPwS004+QaIZh5my18xd77GyOi4OkfYXnKGvXGtZG+NKdCGoxWREQymgzX5PfixYv07t073vb69eu7dZ2TZF4hmDlGGH9wnpdZb7++KQ0a9camPnMiImLlkuB0584d8uXLF2973rx5uXPnjiuGIFmANSz9yGE+Zbfjg/65bCk3cNoMhXJbbs2loOeclfrMiYhIbFqwI5lC7J5zCfotGLovAnOkpVHv6qehcvJmiqz97DyA0TRkBPUVmkRExMZlwem7775j586ddtuOHz8OQPv27eMdbzKZWLVqlUvGJhmbU+UG5v1paaFyJwYalYHlvZPdc+5rOhNAJbVPERGRBLksOB0/ftwWlOJas2ZNvG0pabkiWdMxwhIOTYYBb22GNzZbXj/xIMzpCrmc+6v9Li2oTCH8KaP2KSIikiSXBKfg4GBXXEayqCr42W6h2YmKhoErLbNNAC83gncec7pR71Ra8xKN0nKoIiKSxbkkOJUrV84Vl5HsJBWNek3AewpNIiKSAlocLhmO9em5KvfWGR0jzH62KXaj3nxesNS5Rr0PUoRPaa/1SyIikmIKTpKhxH56zgMTU2jFDs7eP2DPOUuNpovJb9S7hmcUmEREJFUUnCRDCMHMds7aPT0Xg8E41t0/aPkRePIHuHUXahWzhKZSzlVkn0prhSYREUk1BSdxqxDMTGcXH7I9sWIDMGMXjFxjWSHetjIsTl6j3kcpmdqhioiIKDiJ61nXMO3lPOPjtkuJKzoGxvwK0++15hlcBz5tDzmc70+tlikiIpJWFJzEpZyqAG4Vt1Hve61gbPIa9ZpALVNERCTNKDiJyzhVAdzq4r1GvXvuNeqd1w0eT16j3rqU5EeeUGgSEZE0o+AkLrOds86Fpn8uQ4f5lrIDKWzUawKFJhERSXMKTuIS1lt0SdoYDN3uNeqt7Ae/JL9Rrycm3Z4TEZF0oeAk6c7pW3RxG/Uu6w2FnW/Ua7WM3nSkagpHKyIikjDnH00SSaFEm/SCpVHvm5ug7zJLaHriQVj/bIpCE8BxwlL0PhERkaRoxknSXYJNeiHVjXodaUTy1kOJiIg4SzNOku5K48srNIm/49ptaPudJTR5mmBmR5jcKlWhqS+1qEvpVIxWREQkYZpxEpcoQC77DSls1BuXByaeogaV8KMDVRSaREQkXSk4SbqbyAbeYev9DX+ch47zU9SoNzYPYCeBCksiIuIyCk6S5qwtVargxwL+tg9Ny4/AUz/CzTuWRr0/PwWlnWvUG5sHMJPOCk0iIuJSCk6SpmK3VIm3IDyVjXqthlCHV2mqOk0iIuJyCk6SJkIws52zPMcK2zZbaIrbqHdQbfisg9ONeq0BzAOYQmvG0igNRy4iIuI8BSdJtUQb96ZBo97PaU81ilAZP80yiYiIWyk4SaokWhU8DRr1AhQiD82pkAajFRERSR0FJ0mV6exyHJoOX4b2sRr1Lu8Njcom+/wemPBXQUsREckgFJwkWWI/MQfwAdvjH7QxGLovthS4rOwHq5+CKoWcOv//4cdxwohBzXpFRCTjUXASO7GDUdzAEnstkwcm6lEy/glS2aj3BFfZyXNEcEdrmkREJMNRcBKbuMFoJp0IpDYQfy1TDAY7OXf/zYYB/9sCkzZZXj/+IMztCrmS91csGoMI7mhNk4iIZEgKTgI4DkaDWUkAlQBYzCHHa5nA0qh30EqYe69R7/hG8G7KGvV6YqLyvduAIiIiGY2CkwBwjLB4wSgag+ns4iN2JByart2G7otg4ylLo97PO8CgOikag9Y0iYhIRqfgJABUwQ8PTHYByQMSD02nrkGH+fDPZUuj3iW9LBXBk2ExPSlPAa1pEhGRTMG50s2S5ZXGl5l0whPL7TVPTIymYcKh6Y/z0GCWJTSVyg+/9092aJpFZ3pRg7qUpjkVFJpERCTD04xTNhf7KbpAahNAJY4TZltn9CHb40enFUfhyR8sjXofKgarkteo1wTs4jk16BURkUxHwSkbS+gpOuvMz1S2xQ9Nn+yCEfca9QZUgsW9wMf5Rr0ewEw6KzSJiEimpFt12VRCT9GFYLbtH8e6+2+IjoFRa+DFe6FpUG1Y+WSyQtMQ6nCaUbYSByIiIpmNZpyyqYSeolvCPzSmDM/y0/0dN+9YGvUuO2J5ncxGvSbgPVozlkZpNHoRERH3UHDKphw9RQcwmrX2B8Zt1Du3KzxRI1nXWkRPepG894iIiGREulWXTcV9is6hw5ehQZAlNBXKDRueTXZo8lSTXhERyUIUnLKxQGqzg0CG8mj8nRuDoeE3llpNlf1gRyA0Kpus86ugpYiIZDW6VZeNxX6qzs63f0LgvUa9DcvA8uQ16n2FJrSmogpaiohIlqPglE3FfaoOSLNGva2pqCa9IiKSJWXLW3WnTp0iMDCQChUqkDt3bipVqsSkSZOIioqyO+6vv/6iSZMm5MqVizJlyvD++++7acRpL95TdVHR0H/5/dA0vhEs6JHs0KQmvSIikpVlyxmnI0eOEBMTw1dffUXlypX5+++/GThwIBEREXzwwQcAhIeH06ZNG1q1asWXX37JwYMHGTBgAAUKFGDQoEFu/gQpE7tKeD5y3t9x7Tb0WAy/BSerUa8nJp7hIb7jL6IxtKZJRESyPJNhGAk0I8tepk6dyhdffMHJkycB+OKLL3j11VcJDQ3Fy8sLgJdffplly5Zx5MgRp84ZHh6Or68vZrMZHx/nW5Kkh6lsYzzrMLDUVbL9oZ++Bu2T16i3FRV4laa2NUwhmG1tWhSaREQks0nO7+tsOePkiNlsxs/v/i2mHTt20LRpU1toAggICOC9997j6tWrFCxYMN45IiMjiYyMtL0ODw9P30E76QO22VUBt4WmP85Dx/lwMcLSqHfVU1CreJLn68EDdmuYSuOrwCQiItlCtlzjFNfx48f55JNPGDx4sG1baGgoxYoVszvO+jo0NNTheSZPnoyvr6/tp0wZ99cvitc6xWrlUWg2xxKaHioGO59zKjSZgI5UTfNxioiIZAZZKji9/PLLmEymRH/i3mY7d+4cbdu2pVevXgwcODBV158wYQJms9n2c/bs2VSdLy1MZ5fjRr1dF1laqQRUgq39oXTStxI9gK/prNklERHJtrLUrboxY8bQr1+/RI+pWLGi7Z/Pnz9PixYtaNiwITNnzrQ7rnjx4ly8eNFum/V18eKOZ2a8vb3x9na+6W16C8HMB2y/vyE6Bl76FT7eZXk9sDZ81h5yeiZ6nsHUoTc1tIZJRESyvSwVnIoUKUKRIkWcOvbcuXO0aNGCOnXqMHv2bDw87Cff/P39efXVV7lz5w45c1qeQFu3bh1Vq1Z1uL4pI3qbLfdfxG3UO+UxGNcoyUa9HsBEmiowiYiIkMVu1Tnr3LlzNG/enLJly/LBBx9w+fJlQkND7dYuPfXUU3h5eREYGMihQ4dYtGgR06dPZ/To0W4cufMmsoGv2Gt5cfEGNJ9jCU3enrCwB4xvnGRo8sTETN2aExERsclSM07OWrduHcePH+f48eOULl3abp+1OoOvry+//vorw4YNo06dOhQuXJjXX389w9Zwil2jaQF/8w5bLTsOX7aUGzh1DfxyW9qnNE6855wHsJCe+FNGoUlERCQW1XFKR66q4xS755wHpvsVwTedgm6LLAUuK/vB6qegSqEkzzeV1rxEo3Qbr4iISEaiOk7ZSNyec7bQlMJGve8rNImIiCRIwSmTi9dzLm6j3l7VYV43auUqxZ9cjPf+8fiTi5wUJx8dqapbcyIiIolQcMrkquB3//ZcVDQM/hnmHLDsHN8I3n0MPEx0oarD4FSHUvSihmsHLSIikklly6fqspLS+DKFVpiu3YZ231tCk6cJvuwAU1qBhwlPTHTk/4j7DJ0HJvxxf3VzERGRzELBKZMLYh/jTy/FaPQN/BZMjny5YOWTMPhRwBKOvqITdSnN13TG8158spQa6KRbcyIiIsmgW3WZWAhmBv7xJUanBRB6A0rmJ2bVU+x+eCKnuAZgV1IgkNoEUInjhKkKuIiISAooOGVSIZiZtPIrjN5zLFXBHyoGq54iprQPp7iW4Lql0vgqMImIiKSQglMmFMQ+Bn46EWPEGogxLI16F/cCH0ufvCdYSjhRBFLbzSMVERHJWrTGKZMJwczAN8dgDP/FEpoG1rasafK531zYAAazkhDM7huoiIhIFqTglMkcIwyjTUXIncPSqPerjpDTM95x0RgcJ8wNIxQREcm6dKsuk6mCHx7+ZYk5/iKUzA9YnpCLwYhdBhNPTFTGzz2DFBERyaI045TJlMaXmXTCs6Sll47nvXIDcUsNfKVSAyIiImlOM06ZUEJlBVRqQEREJH0pOGVSjsoKqNSAiIhI+tKtOhEREREnKTiJiIiIOEnBSURERMRJCk4iIiIiTlJwEhEREXGSgpOIiIiIkxScRERERJyk4CQiIiLiJAUnEREREScpOImIiIg4ScFJRERExEkKTiIiIiJOUnASERERcVIOdw8gKzMMA4Dw8HA3j0REREQSYv09bf29nRgFp3R0/fp1AMqUKePmkYiIiEhSrl+/jq+vb6LHmAxn4pWkSExMDOfPnyd//vyYTCZ3D8dp4eHhlClThrNnz+Lj4+Pu4biFvgN9B9n984O+A9B3kF0+v2EYXL9+nZIlS+LhkfgqJs04pSMPDw9Kly7t7mGkmI+PT5b+P4oz9B3oO8junx/0HYC+g+zw+ZOaabLS4nARERERJyk4iYiIiDhJwUni8fb2ZtKkSXh7e7t7KG6j70DfQXb//KDvAPQdZPfP74gWh4uIiIg4STNOIiIiIk5ScBIRERFxkoKTiIiIiJMUnEREREScpOAkIiIi4iQFJ7E5deoUgYGBVKhQgdy5c1OpUiUmTZpEVFSU3XF//fUXTZo0IVeuXJQpU4b333/fTSNOH++88w4NGzYkT548FChQwOExZ86coUOHDuTJk4eiRYsyduxY7t6969qBpqPPPvuM8uXLkytXLurXr8/u3bvdPaR0s2XLFjp16kTJkiUxmUwsW7bMbr9hGLz++uuUKFGC3Llz06pVK44dO+aewaaDyZMnU7duXfLnz0/RokXp2rUrR48etTvm9u3bDBs2jEKFCpEvXz569OjBxYsX3TTitPfFF1/w0EMP2apj+/v788svv9j2Z/XPH9eUKVMwmUyMHDnSti27fQeJUXASmyNHjhATE8NXX33FoUOHmDZtGl9++SWvvPKK7Zjw8HDatGlDuXLl2Lt3L1OnTuWNN95g5syZbhx52oqKiqJXr14MHTrU4f7o6Gg6dOhAVFQU27dvZ+7cucyZM4fXX3/dxSNNH4sWLWL06NFMmjSJffv2UatWLQICArh06ZK7h5YuIiIiqFWrFp999pnD/e+//z4zZszgyy+/ZNeuXeTNm5eAgABu377t4pGmj82bNzNs2DB27tzJunXruHPnDm3atCEiIsJ2zKhRo1i5ciVLlixh8+bNnD9/nu7du7tx1GmrdOnSTJkyhb179/LHH3/QsmVLunTpwqFDh4Cs//lj27NnD1999RUPPfSQ3fbs9B0kyRBJxPvvv29UqFDB9vrzzz83ChYsaERGRtq2jR8/3qhatao7hpeuZs+ebfj6+sbbvnr1asPDw8MIDQ21bfviiy8MHx8fu+8ls6pXr54xbNgw2+vo6GijZMmSxuTJk904KtcAjJ9++sn2OiYmxihevLgxdepU27Zr164Z3t7exoIFC9wwwvR36dIlAzA2b95sGIbl8+bMmdNYsmSJ7ZjDhw8bgLFjxw53DTPdFSxY0Jg1a1a2+vzXr183qlSpYqxbt85o1qyZMWLECMMwsu/fgYRoxkkSZTab8fPzs73esWMHTZs2xcvLy7YtICCAo0ePcvXqVXcM0eV27NhBzZo1KVasmG1bQEAA4eHhtv9CzayioqLYu3cvrVq1sm3z8PCgVatW7Nixw40jc4/g4GBCQ0Ptvg9fX1/q16+fZb8Ps9kMYPv//d69e7lz547dd1CtWjXKli2bJb+D6OhoFi5cSEREBP7+/tnq8w8bNowOHTrYfVbIfn8HkpLD3QOQjOv48eN88sknfPDBB7ZtoaGhVKhQwe44a4AIDQ2lYMGCLh2jO4SGhtqFJrD/DjKz//77j+joaIef78iRI24alftY/zwdfR+Z/c/akZiYGEaOHEmjRo2oUaMGYPkOvLy84q33y2rfwcGDB/H39+f27dvky5ePn376ierVq3PgwIFs8fkXLlzIvn372LNnT7x92eXvgLM045QNvPzyy5hMpkR/4v5SPHfuHG3btqVXr14MHDjQTSNPOyn5DkSym2HDhvH333+zcOFCdw/F5apWrcqBAwfYtWsXQ4cOpW/fvvzzzz/uHpZLnD17lhEjRvD999+TK1cudw8nw9OMUzYwZswY+vXrl+gxFStWtP3z+fPnadGiBQ0bNoy36Lt48eLxnqSwvi5evHjaDDgdJPc7SEzx4sXjPWWWGb4DZxQuXBhPT0+Hf8aZ/bOlhPUzX7x4kRIlSti2X7x4kYcffthNo0ofL7zwAj///DNbtmyhdOnStu3FixcnKiqKa9eu2c04ZLW/E15eXlSuXBmAOnXqsGfPHqZPn84TTzyR5T//3r17uXTpErVr17Zti46OZsuWLXz66aesXbs2y38HyaHglA0UKVKEIkWKOHXsuXPnaNGiBXXq1GH27Nl4eNhPSvr7+/Pqq69y584dcubMCcC6deuoWrVqhr5Nl5zvICn+/v688847XLp0iaJFiwKW78DHx4fq1aunyTXcxcvLizp16rBhwwa6du0KWG7fbNiwgRdeeMG9g3ODChUqULx4cTZs2GALSuHh4bZZiazAMAyGDx/OTz/9xKZNm+Ldiq9Tpw45c+Zkw4YN9OjRA4CjR49y5swZ/P393TFkl4iJiSEyMjJbfP7HHnuMgwcP2m3r378/1apVY/z48ZQpUybLfwfJ4u7V6ZJxhISEGJUrVzYee+wxIyQkxLhw4YLtx+ratWtGsWLFjD59+hh///23sXDhQiNPnjzGV1995caRp63Tp08b+/fvN958800jX758xv79+439+/cb169fNwzDMO7evWvUqFHDaNOmjXHgwAFjzZo1RpEiRYwJEya4eeRpY+HChYa3t7cxZ84c459//jEGDRpkFChQwO4pwqzk+vXrtj9jwPjoo4+M/fv3G6dPnzYMwzCmTJliFChQwFi+fLnx119/GV26dDEqVKhg3Lp1y80jTxtDhw41fH19jU2bNtn9f/7mzZu2Y4YMGWKULVvW+O2334w//vjD8Pf3N/z9/d046rT18ssvG5s3bzaCg4ONv/76y3j55ZcNk8lk/Prrr4ZhZP3P70jsp+oMI3t+BwlRcBKb2bNnG4DDn9j+/PNPo3Hjxoa3t7dRqlQpY8qUKW4acfro27evw+9g48aNtmNOnTpltGvXzsidO7dRuHBhY8yYMcadO3fcN+g09sknnxhly5Y1vLy8jHr16hk7d+5095DSzcaNGx3+efft29cwDEtJgtdee80oVqyY4e3tbTz22GPG0aNH3TvoNJTQ/+dnz55tO+bWrVvG888/bxQsWNDIkyeP0a1bN7v/oMrsBgwYYJQrV87w8vIyihQpYjz22GO20GQYWf/zOxI3OGXH7yAhJsMwDBdOcImIiIhkWnqqTkRERMRJCk4iIiIiTlJwEhEREXGSgpOIiIiIkxScRERERJyk4CQiIiLiJAUnEREREScpOIm4ybFjx+jWrRslSpTAw8MjXudxkbRiGAZ16tShTZs2dtubN2+OyWRy06gy3jic4Wis69evx2QysXr1ajeNSlxJwUkkjlOnTmEymex+cubMSalSpXj88cf5448/Un2N6OhounbtyurVq+nQoQOvv/46L7/8chqMPnt444034v0Zxf1544033D3MDGPevHns27ePt956y91DSZGlS5diMpn4+eef3T0Uh1q1akXjxo0ZN24c0dHR7h6OpDM1+RVJQKVKlXjmmWcAiIiIYO/evSxZsoRly5axfv16mjZtmuJzBwcH888//zBw4EBmzpyZVkPOdnr06EGNGjUc7mvevLlrB5NBxcTE8MYbb9CkSRMaNGjg7uGkyPLly8mbNy+tWrVy91ASNG7cODp37szChQt5+umn3T0cSUcKTiIJqFy5crxZiylTpjBhwgRee+01Nm/enOJznz9/HoCSJUumZojZXs+ePendu7e7h5Gh/fLLL5w6dYpXX33V3UNJkbt377Jq1SoCAgLIlSuXu4eToLZt21K4cGG+/PJLBacsTrfqRJIhMDAQgL1798bbFxUVxUcffUTt2rXJmzcv+fPnp0mTJqxYscLuuPLly9OsWTMA3nzzTYe3lpw9F0C/fv0wmUycPHmSDz/8kOrVq+Pt7U2/fv1sx1y6dIlRo0ZRuXJlvL29KVy4MD169ODvv/+Od77y5ctTvnx5bty4wYgRIyhZsiTe3t489NBDLF261OH3EhUVxbRp06hbty758+cnX758VK9endGjR3P16lW7Y5MzlrQyZ84cTCYTc+bM4ddff6Vhw4bkyZOHQoUK0bdvX65cueLwfX/99Re9e/emRIkSeHl5Ua5cOYYPHx7veOvt3X79+nH48GG6detGoUKFMJlMnDp1CoCbN28ybtw4ypQpQ65cuahRowZff/01mzZtsvvzN5vN5M2blwcffNDhmGJiYihfvjwFCxbk1q1bSX722bNnYzKZ6NGjh9Pf16JFi/D29qZWrVpcuHDBtt0wDGbPnk2TJk0oUKAAefLkoUqVKgwePJgzZ87Yjtu7dy8vvPACNWrUwNfXl9y5c1OzZk2mTJnCnTt3nB4HwNatW7l69SpdunSxbbOuM4qMjOSVV16hbNmy5M6dmzp16rB+/XrA8j0OGzaMkiVLkitXLvz9/dm9e7fDa/z99988/vjjFC1aFG9vbypUqMDIkSMT/HvhSM6cOenatSu///47x48fT9ZnlEzGvT2GRTKe4OBgAzACAgLi7bt06ZIBGL6+vnbbb9++bTRv3twAjIcfftgYPny4MWTIEKNMmTIGYHzyySe2Y6dNm2b07dvXAIxmzZoZkyZNMiZNmmRs3Lgx2ecyDMN2rvbt2xt+fn5Gnz59jHHjxhkffPCBYRiGcfz4caN06dIGYLRp08YYM2aM0adPHyNPnjxG3rx5jZ07d9qdr1y5ckbJkiUNf39/o1q1asYLL7xgDBgwwMiTJ49hMpmMtWvX2h1/8+ZNo1GjRgZgVKlSxRg+fLjx0ksvGV26dDHy5Mlj7N+/33ZscseSkEmTJhmAsWDBAqeOnz17tgEY3bp1M7y8vIwePXoYY8aMMerWrWsARqNGjeK9Z/ny5Ya3t7eRO3duo3fv3sbYsWONDh062D5nWFiY7Vjr35lGjRoZPj4+RqNGjYzRo0cbffv2Nc6dO2fcvXvXaNGihQEYNWvWNMaNG2c899xzRv78+Y1OnToZgDFp0iTb+QYMGGAAxrZt2+KNa82aNQZgDBs2LMnPHRMTY/j5+RnVqlVzuL9Zs2ZG3F8DM2bMMEwmk9G0aVPj2rVrtu3R0dFGz549DcAoVaqUMWTIEGPcuHHG448/bhQoUMD46aefbMcOHjzYKFmypO17GzZsmPHggw8agNG9e3enxmH14osvGp6ensaVK1fiHd+lSxejYsWKxrBhw4wBAwYY3t7ehre3t/HHH38YtWvXNmrUqGG8+OKLxpNPPml4eHgYBQsWtPtMhmEYW7duNfLkyWPkyJHD6N27t/Hyyy/bzl+pUiXj8uXLTo81KCjIAIyvvvrK4X7JGhScROJILDi9++67BmB06NDBbvsrr7xiAMZrr71mxMTE2LaHh4cbjz76qOHl5WWcO3fOtn3jxo3xflmm9FzW4FS6dGnj9OnT8c7XsGFDw9PT01izZo3d9qNHjxr58+c3atasabe9XLlytl9KkZGRtu3r1693+L2MGTPGAIw+ffoYd+/etdt37do14/r16ykeS0KswalHjx624Bn358KFC7bjrcEpR44cxu+//27bfvfuXVtI3bFjh237f//9Z/j4+BilSpUyTp06ZXftBQsWGIDxwgsv2LZZ/84Axuuvvx5vvLNmzTIAo127dnbf0aFDh4xcuXLF+7uwa9cuAzD69esX71zW8HLgwIEkv6dDhw4ZgPH000873B83BFj/7nXr1s24deuW3bGffPKJARiPPfaYcfPmTbt9N2/etAs2p0+fjvd3ISYmxhYIY/8ZOBpHbOXLlzeaN2/u8PjGjRsbN27csG1ftGiRARgFChQwevXqZdy5c8e277333jMA48MPP7Rti46ONipVqmQA8f5Ojh071gCMAQMGOD3WP//80wCMZ5991uF+yRoUnETisP4SrFSpku2X8EsvvWSbMShWrJjxzz//2I6Pjo42ChYsaFSqVMku6FitWLEi3kxRQsEpJeeyBqfp06fHO37fvn0O/+VvNXr0aAMwDh48aNtmDU4nT56Md3y5cuUMPz8/2+s7d+4Y+fPnN3x9fe1mYBxJyVgSYg1Oif3EnumyBidHv9Cs+2bMmGHb9tFHHxmAMW/ePIfXr127tlG4cGHba+vfmeLFi9uFTStrONu3b1+8fYMGDXL4d+GRRx4x8ubNa5jNZtu2S5cuGV5eXkbdunUT/G5iW7t2rQEYo0ePdrjfGgLu3r1rBAYGGoAxcODAeKHHMAzjgQceMDw9PY1///3XqWs7snfvXgMw3njjDYfjiOvAgQMGYEybNs3h8Zs3b7bbHh0dbeTMmdMA4v1HxJkzZ+L9HdiyZYst0MZ1/fp1w8/Pz8iVK5fdn2liwSk0NNQAjJYtWzr+AiRL0OJwkQScOHGCN998025b8eLF2bp1K5UrV7ZtO3r0KFevXqVkyZLxjge4fPkyAEeOHEnymqk5V7169eJt27lzJwAXL150+Hi+9TxHjhyxezqtQIECVKhQId7xpUuXZseOHXbvv379Oq1ataJgwYKJfraUjiUxCxYsSNbi8Dp16sTbVrp0aQCuXbsWb6y7du3ixIkT8d5z+/Zt/vvvP/777z8KFy5s216rVi28vLziHf/nn3+SN29eHnnkkXj7GjVq5PDJysGDBzNkyBDmz5/PkCFDAEtZgaioKAYOHJjEJ7WwrtFJqkZYjx49WL58Oa+++ipvv/12vP03btzg8OHDVK5cmSpVqiR53aioKD799FMWLlzIkSNHuHHjBoZh2PZbH45IyvLlywHs1jfF9vDDD9u99vDwoGjRoty8eZOyZcva7StRokS8a+/fvx9w/ARmvnz5ePTRR/n11185evQoNWvWTHK8fn5+APz3339JHiuZl4KTSAICAgJYs2YNYAksc+fOZfz48XTu3Jndu3eTL18+AMLCwgA4dOgQhw4dSvB8ERERSV4zNecqVqxYgudbtWoVq1atcvp8vr6+Do/LkSMHMTExttdmsxmAUqVKJXju1I4lLfn4+MTbliOH5V+DsevvWMf62WefJXq+iIgIu+Dk6M8AIDw8nDJlyjjcl9B7nnrqKV566SVmzZplC05BQUHky5ePJ598MtFxWeXOnRuwBL3EbNmyhVy5ctG+fXuH+5Pz5wyWpx1XrlzJ//3f//HEE09QtGhRcubMybVr15g+fTqRkZFOnWfZsmXUrFnTYYiHhP88E/tzjr04PTw8HEj4z8AatqzHJcW6WD9PnjxOHS+Zk56qE3FCkSJFeOmll3jllVc4fPgwEydOtO2z/ku6R48eGJbb3w5/Zs+eneR1UnMuR5WXref75JNPEj1f3759U/S9WGcyzp075/RnS6+xpCXrWA8ePJjoWMuVK2f3voSqX/v4+NhmC+O6ePGiw+358+fn6aefZu/evRw4cIBt27Zx+PBhevfubQvtSSlSpAhwPwgmZMOGDeTJk4e2bduyffv2ePutQdqZP+c9e/awcuVKAgIC+Oeff/j666955513eOONN5I1O3jmzBn2799P165dnX5Pcln/nBP6MwgNDbU7LinW79n6vUvWpOAkkgyvvPIKJUuW5PPPP7c9Zv7AAw/g4+PDH3/8kexHreNKy3MB1K9fH8Du9lpaqlq1Kj4+PuzZsyde2QFXjyUtpfVYa9WqRUREBAcOHIi3z1FQsRo8eDAAX3/9NbNmzQJw+jYdwIMPPoiHhwdHjx5N9LhHHnmE3377DS8vL9q2bcu2bdvs9lvLSwQHB3Ps2LFEz2W9tdmhQwc8PT3t9m3dutXpsVtLbyR0my4tWG+dbtq0Kd6+iIgI/vjjD3Lnzk3VqlWdOp/1e3bmtp5kXgpOIsmQO3duxo8fz507d/jf//4HWG4BDB06lNOnT/PSSy85DDx///03ly5dSvL8aXkusKx7ql+/PgsWLGDRokXx9sfExKSqkGeOHDkYPHgwZrOZESNGxGs3YTabuXHjhkvGkpb69+9P/vz5efXVVx3eMr1586ZtHZQzrAURJ06caHer88iRI8ydOzfB9z3yyCPUrVuX77//niVLlvDQQw85XMuWkAIFCvDQQw/xxx9/2F3XkVq1avHbb7/h7e1N27Zt+f333+32Dxs2jOjoaJ5//vl49aNu375tm22xzsLFff+hQ4eYPHmy02Nfvnw5pUuXdrguLa00atSISpUq8csvv9jqP1m9/fbbXLlyhSeffNLhujVHdu3aBWCr0yZZk9Y4iSTToEGDeO+995g3bx6vvPIKlSpV4s0332Tfvn3MmDGDVatW0bRpU4oWLcq5c+c4ePAgf/75Jzt27KBo0aJJnj8tzwWWBdQtWrSgd+/efPzxx9SuXZvcuXNz5swZduzYweXLl5NcA5OYt956i507d/Ltt9+yc+dO2rVrh7e3NydPnmTNmjX8/vvvtkW8aT2WpUuXJrjovlq1aimuKl6kSBEWLFhAr169qFWrFm3btqVatWpERkZy6tQpNm/eTMOGDW1r4JLSv39/vv32W1atWsUjjzxCu3btCAsLY+HChbRu3ZqVK1fi4eH4v2OHDBliK7yanNkmq27dujFp0iR27txJw4YNEz32oYce4rfffuOxxx6jXbt2rF69miZNmgAwdOhQNm/ezOLFi6lSpQqdO3fGx8eHM2fOsHbtWoKCgujatSv16tWjXr16LF68mAsXLtCgQQPOnDnDihUr6NChQ4JFVGO7du0amzdvTtHnTQ4PDw/mzJlDQEAA7du3p1evXpQrV44dO3awadMmKlWqxJQpU5w+37p16yhYsGCq2jFJJpC+D+2JZD6J1XGysta06dOnj23b3bt3ja+++spWBNHb29soW7as0bZtW+OLL76wqzeTWB2n5J7LWo4gODg4wfGGhYUZEydONGrUqGHkzp3byJcvn1GlShXjqaeeMn788Ue7Y8uVK2eUK1fO4XkSehT79u3bxgcffGA8/PDDtvNXr17dGDNmjHH16tUUjyUhzpQj6NKli+14a8mB2bNnxztXYn8WR44cMQIDA41y5coZXl5eRsGCBY2aNWsaL774orF7927bcda/M3379k1wzDdu3DDGjBljlCxZ0vD29jaqV69uzJw501i6dKnDR+6tIiIibIU4436Xzjh37pyRI0cOY+jQofH2JfTnefDgQaNo0aJG3rx57R75j4mJMWbNmmU0aNDAyJs3r5EnTx6jSpUqxpAhQ4wzZ87Yjrt06ZIxYMAAo2TJkkauXLmMmjVrGp999plx8uRJh99T3HF8//33BmD8+uuvDj9TYiUBEvv7y72is3H99ddfRs+ePY3ChQsbOXPmNMqVK2eMGDEiXvHLxK4dHBxsmEwmY+TIkQ6vLVmHyTBiPSMqIiIuNXHiRN555x1Wr15Nu3bt4u3/448/qFu3Ln369GHevHkpukafPn1YtWoVp0+fJn/+/Kkdcrp74oknWLt2LZcvXyZnzpzuHo5TJk6cyPvvv8/hw4epVKmSu4cj6UhrnEREXCB2zzerf/75hxkzZlCgQAGHtYQApk6dClhulaXU22+/za1bt/jkk09SfA5XiYqKYs2aNbRr1y7ThKarV6/yySefMHToUIWmbEBrnEREXGDo0KGcOnWKevXqUbBgQU6cOMHKlSu5c+cOQUFBtppLYHkUf/78+Rw6dIjFixcTEBCAv79/iq9drlw55s6dm+Bj9xmJl5eXrW5UZhEcHMyoUaMYPny4u4ciLqBbdSIiLvD999/z5ZdfcvjwYcxmM/ny5aNu3bqMGTOGgIAAu2M3bdpEixYtyJcvHy1atGDmzJkUL17cTSMXkdgUnEREREScpDVOIiIiIk5ScBIRERFxkoKTiIiIiJMUnEREREScpOAkIiIi4iQFJxEREREnKTiJiIiIOEnBSURERMRJCk4iIiIiTlJwEhEREXGSgpOIiIiIkxScRERERJyUw90DyMpiYmI4f/48+fPnx2QyuXs4IiIi4oBhGFy/fp2SJUvi4ZH4nJKCUzo6f/78/7d33+FRVF0cx7+7AQIYkhAJCb036SAllFAFpSNFEOkgRQEpoigI2EBREVRelK6CUpQSQBAxikAoAkFFREBaqEJkAxECSeb9Y8maJW2TbPrv8zz7yM7cmXt3EtnDnTvnUKJEiYwehoiIiDjg3LlzFC9ePNE2CpzSUIECBQDrD8Ld3T2DRyMiIiLxCQsLo0SJErbv7cQocEpDMbfn3N3dFTiJiIhkco4sq9HicBEREREHKXASERERcZACJxEREREHKXASERERcZACJxEREREHKXASERERcZACp2zi9OnTmEwmu1fu3LkpVqwYPXv25Oeff473uAEDBtjaf/jhhwme/4knnrC1W7p0qd0+wzD4/PPPadmyJQ8++CB58uTBx8eH2rVrM3LkSH788Ue79tOmTbMbp4uLC56enlSsWJEePXqwZMkSwsPDU31NYuzYsYMJEybQokULPDw8MJlMDBgwINnnuXz5Ms8++ywNGjTAx8cHV1dXihcvTqtWrfj6668xDCPe4w4ePEiPHj0oU6YM+fLlo1SpUnTu3JkdO3bEafvDDz/E+TnGft1/7UVEJH0pj1M2U65cOZ566ikAwsPDOXDgAKtXr2bdunV89913+Pv7x3tcrly5WLx4Mc8++2ycfaGhoaxfv55cuXIRGRkZZ/+gQYNYunQpBQsWpEOHDhQrVoxbt25x+PBhFi1aRFhYGM2aNYtzXLdu3ahWrRpgTT52+vRpfvjhB9asWcMrr7zCZ599RvPmzVNxNawWL17MsmXLyJ8/PyVLliQsLCxF5zl37hyffvopDRs2pGvXrnh5eXHlyhUCAgLo1q0bQ4YMYcGCBXbHrFu3jm7duuHq6krXrl0pUaIE586dY+3atWzYsIElS5bEG8Q1a9Ys3s9eq1atFI1dREScxJA0Y7FYDMCwWCxp3tepU6cMwGjbtm2cfTNmzDAAw9/fP86+/v37G4DRsWNHAzCCg4PjtJkzZ44BGJ06dTIAY8mSJbZ9O3bsMACjVq1a8X7Of/75x9i1a5fdtqlTpxqA8cUXX8Rpf/v2bWPmzJmG2Ww2HnjgAePw4cOOfPxE7d+/3/jtt9+MyMhIIygoyACM/v37J/s8d+7cMSIjI+NsDwsLM6pUqWIAxm+//Wa3r0qVKobJZDIOHTpkt/3AgQOGyWQyypQpY7c9MDDQAIypU6cme3wiIpIyyfm+1q26HGDw4MEAHDhwIME2/fv3x8XFhUWLFsXZt2TJEqpUqYKfn1+cfUFBQbbj48uO7unpSaNGjRweq6urKy+88AKvvPIK4eHhvPjiiw4fm5CHH36YqlWr4uLikqrz5M6dO95zFChQgEcffRSAEydO2O3766+/KFKkSJyZojp16lCkSBH+/vvvVI1JRETSlwKnHCRXroTvzBYrVow2bdqwYsUK7ty5Y9t+8OBBgoODGThwYLzHPfjggwD8+eefTh3r+PHjyZ8/P1u3bsVisdi2x6wBcsYtPGe5ffs233//PSaTiapVq9rtq1atGhcvXiQ4ONhu+8GDB7l48SKtWrWK95zHjx/n/fffZ8aMGXz22WecP38+rYYvIiLJoDVOOcDChQsBaNKkSaLtBg8ezDfffMP69evp0aMHAIsWLSJXrlz069ePJUuWxDmmbdu2uLu7M3/+fCwWC127dqVevXqUKlUqVWN2c3Ojbt26/PTTTxw4cICWLVum6nzOdOXKFebNm0d0dDRXrlxh8+bNnDt3jqlTp1K+fHm7trNnz6Z9+/Y0atSIxx9/nBIlSnD27FnWrl1L8+bNmT9/frx9rFixghUrVtje58qVi1GjRjFr1qxUz5yJiEjKKXDKZk6cOMG0adOA/xaHBwYG4uPjw6xZsxI9tlOnThQqVIjFixfTo0cPbt++zRdffEH79u3x8fGJ95jixYvz1VdfMXjwYLsve29vb1q0aMGwYcNSHPQULVoUgKtXr9q21a9fn6NHj5I/f/4UndMZrly5wvTp023vc+fOzaxZsxg/fnyctk2bNuWnn36iR48eLF++3La9VKlSDBgwAF9fX7v23t7ezJw5kw4dOlC6dGnCw8MJCgrixRdfZPbs2ZhMJt599920+3AiIpIo3arLZk6ePMn06dOZPn0677zzDoGBgfj6+rJz506qVKmS6LG5c+fmqaee4ttvv+X8+fOsXbuWf/75h0GDBiV6XOvWrTl58iTbtm1jypQptGvXjoiICFatWkWrVq146aWXnPb58ufPT+XKlSlZsqTTzplc1apVwzAMIiMjOXXqFNOnT+fll1+mW7ducZ463LRpE/7+/tSrV4+jR4/y77//cvToURo3bkz//v2ZOHGiXfuqVavywgsvULVqVR544AEKFy5M586dCQwMxNvbm7lz53LlypX0/LgiIhKLAqdspm3bthiGgWEYXLlyhVmzZnHlyhU6derEzZs3kzx+0KBBREdHs3TpUhYvXoyvry/t2rVL8rhcuXLRunVrXn31VTZt2sS1a9dYsGABuXLlYsaMGRw8eDDZn+XChQuAdRYmM3JxcaF06dJMmjSJ119/nbVr19qlI7h27Rp9+vShQoUKfPbZZ1SuXJl8+fJRuXJlPvvsM+rWrct7773H2bNnk+zL19eXzp07ExkZyd69e9PyY4mIZFohWAjkFCFYkm6cRhQ4ZWPe3t5MmDCBl156iaNHjzJ58uQkj6levTr16tXjo48+4vvvv6dfv36JLipPSK5cuRgyZAhPPvkkAIGBgck6/ubNmxw4cAAXFxfq1KmT7P7TW5s2bQDr4vUYu3fvxmKx0KxZM8xm+//VzGYz/v7+REVF8csvvzjUR6FChQCcmhxURCSrWMRBSq4dRsvwBZTifRaR/H+QO4MCpxzgpZdeomjRosybN4/Tp08n2X7QoEFcvHiR6OjoJG/TJcXNzS1Fx7377rv8+++/PPbYY3h4eKRqDOkhZnYsd+7ctm0xTycmlHIgZrurq6tDfcTMNJUuXTqlwxQRyZLOGdcZMmUsxuMr4cmviY6KYhgBGTLzpMApB8iXLx8vvPACd+/e5bXXXkuy/VNPPcXatWv55ptvqFSpUqJtt2zZwvr16+PNKH7ixAlWr14NJP1EX4yIiAjefvttXn31Vdzc3JgxY4bd/n///Zc//vjDodtbKZVQH4cPH+bu3btx2oeGhtrWccW+rdmgQQNcXFxYs2ZNnFml4OBg1qxZQ/78+WnQoIFte0K5tubMmUNgYCAVKlSgXr16Kf5sIiJZTUREBIP6DoDX75WpqlEYzCaiMDhBaLqPR0/V5RBPP/00b731Fp9++ikvvfQS5cqVS7Ctm5sbXbp0cei8f/zxB2PHjqVQoUL4+/tTrlw5DMPgxIkTbN68mTt37jBixAi74CDGmjVr+OOPPwDrrblTp06xY8cOrl69SokSJfj8889tJVli7Nu3jxYtWtCsWTO722KJ2blzpy0lQ8wsz86dO22lTgoVKsQ777yTZB+zZ89m48aNNG7cmJIlS5IvXz7OnDnDpk2bCA8Pp0ePHvTu3dvWvnjx4rzwwgu8+eab1KtXj65du1KqVClOnz7NunXruHPnDnPnzrVLHNqtWzdy587Nww8/TPHixQkPD2fPnj0cOnQIT09PPv/8c6UjEJEcIzQ0lK5du1pre+Yyw8cdYFBtAFwwUR6vdB+TAqccIm/evEyaNIlRo0Yxffp0Pv30U6ect0+fPri5ubF161Z+/fVXtm3bxu3btylUqBBt2rRhwIABdOvWLd5jv/rqK7766ivMZjNubm4ULlyY5s2b0759e3r27Om0lAMnTpxg2bJldttOnjzJyZMnAWtqgNiBU0L69u1LdHQ0e/fuJTAwkFu3bvHggw/i7+9P//79eeKJJ+Ic88Ybb1CjRg0+/vhjtm7dyo0bN/Dw8KBFixaMGTOGxx57zK79iBEj2Lp1Kzt27ODatWuYzWZKlSrFc889x/jx4ylevHgqroSISNbx119/0a5dO44dO4a7uzuD18xg7iN/E4WBCyY+piPFSf+lHCbDSKCku6RaWFgYHh4eWCyWeMuRiIiISFx79+6lY8eO/P3335QoUYJNmzZRvXp1QrBwglDK4+XUoCk539eacRIREZFM4+uvv6ZPnz7cvn2bOnXqEBAQYEuIXByPDJllik2Lw0VERCTDGYbB7Nmz6d69O7dv36Z9+/b8+OOPtqAps1DgJCIiIhkqMjKSUaNGMW7cOAzDoN/IITy3bjbX3aIyemhx6FadiIiIZJibN2/Su3dvNm7ciMlkosc7z/HZWHc+NS3HjIlP6MhgMk8iZM04iYiISIa4ePEizZo1Y+PGjeTNm5f5q5eyZpwHhsm6PxojwxJdJkSBk4iIiKS73377jYYNG3Lw4EG8vb2tSX67NSUa+4f9MyrRZUIUOImIiEi6CcHCO999RsPGjTh79ixlK5YnKCiIhg0bUgEvzJjs2mdUosuEKHASERGRdLGIg5Rc0p/nHxtAeNgNaFqSU0GP80M566244njwCR1xuRc8ZWSiy4QoAWYaUgJMERERq3PGdUq+0vm/mnNPVofFncA1Fy6YOM1ztgAprRJdJkQJMEVERCTTiIiIYNDgAbD8XtA0uSm82gJM1pmlmHVMMUFSZkh0mRAFTiIiIpJiIVg4TigVEpgd+ueff+jatSs//vgjuJishXoH26cXyGzrmBKjwElERERSZBEHeZoAojHizbmUWKHeGJlxHVNiFDiJiIhIsoVgsQVN8F/OpRoU5iZ3ubn3LwZ37B2nUO+4e+uXHiA34dxNt3VMzqLASURERJLtOKHx5lyqz0JYexSe/BpuR1Ktdg1e2fgxBYuWBDL3+iVHKB2BiIiIJFt8OZcwDJgdBN1Wwe1IaF+B33a0p2fRLZTifRZxMGMG60QKnERERCTZ7s+5ZIoyYPQ3MO5bMIARD8O6XuCWB8ic5VNSQoGTiIiIpEhbyrGCbnwa3o5qXQPhw/3WHe88Ah+1g1z2YUZmK5+SElrjJCIiIslme6LuYhh0/AIOXIS8ueCzrtD9oXiPMUOWSTuQEM04iYiISLKEYGEoG4g+chkaLrIGTYXy80zgh7h0r5rgcTN5JEsvDAfNOImIiEgyzWEvxva/4PFVEBYBFR+EzU/SvVwbXsSLE4TyMxd4ke+Iupfj6S1aM4HGGT30VFPgJCIiIkmKyRDuRm7eXToPhgZAZDQ0LWldBO6Vj/1coDllKI4HzSlDL6qla8259KDASURERGxCsLCbcwCUwZNTXOd7TrGAg0Qb0TD1B3jtXs253tVgSWdwtYYTk/iO3lTLEjXnUkqBk4iIiADWBd9D2XBfWst7IiJhSAB8/ov1/cv3CvWa/8vldH+x3uxIgZOIiIjYFnzHGzT9cwu6roQfzyRYqBeyVrHelFLgJCIiIhwnNP6g6dQ/0G4F/HEVCuSBNT2hTbk4zbJasd6UUuAkIiIiVIhvpmjfeWuOpivhUMIdNj0J1X3smrhg4gu64UeJbB80gQInERGRHCvmSbmYoMkE/806rT0Kfb6GW5FQ2xc2PglFC9gdHzPL1INq6TrujKTASUREJAeyZf6+l2dpHH7WoMkw4P09MP5ezbl2FWBld1vNOYD/0Y7KeGerNAOOUuAkIiKSw4RgsQVNYC3A+w67ISoantvyX825EQ/D3Mfsas6ZgA5UynEBU4xsW3Jlx44ddOzYkaJFi2IymVi3bp3dfsMweOWVVyhSpAj58uWjdevWHD9+3K5NaGgoffr0wd3dHU9PTwYPHszNmzfT8VOIiIg433FCbUGTTfgd65NzSRTqfTsblE1JjWwbOIWHh1OzZk0++uijePe//fbbzJ07l/nz57N3714eeOAB2rZty+3bt21t+vTpw5EjR9i2bRsbN25kx44dPP300+n1EURERJwqBAur+I0/+BtT7B0Xb0CzpRDwp7VQ7+oeML4RmOxa8RJNs0XZlNQwGYYR79OH2YnJZGLt2rV06dIFsM42FS1alPHjxzNhwgQALBYLPj4+LF26lF69enH06FEeeugh9u/fz8MPPwzAli1baNeuHSEhIRQtWjROPxEREURERNjeh4WFUaJECSwWC+7u7mn/QUVERBJwf3JL20LwI1es6QbOWqBQftjQC/xKxDl+FPWZS7t0HHH6CQsLw8PDw6Hv62w745SYU6dOcenSJVq3bm3b5uHhQYMGDQgKCgIgKCgIT09PW9AE0Lp1a8xmM3v37o33vDNmzMDDw8P2KlEi7i+eiIhIeosvuaUBsP0vaLTYGjRVfBD2DI43aGpPhWwbNCVXjgycLl26BICPj30uCh8fH9u+S5cuUbhwYbv9uXLlwsvLy9bmfpMmTcJisdhe586dS4PRi4iIJM9uzsVNbrk0GB5dDmER0KQk7B4E5eLmcupDdTbSJz2GmSXoqToncnV1xdXVNaOHISIiYrOIgwxhw38bDCNuod7Fna1rm+7jgomZtI6zPSfLkTNOvr6+AFy+fNlu++XLl237fH19uXLlit3+yMhIQkNDbW1EREQysxAs9kFTRCT0W/df0PRyU/j88QSDppxQQiW5cuSMU5kyZfD19WX79u3UqlULsC4M27t3LyNGjADAz8+P69evc+DAAerWrQvA999/T3R0NA0aNMiooYuIiDhsN7GWjPxzCx5fBT+cthbqnd8BhvxXqDcmCWZPHiKcuzkyuaUjsm3gdPPmTU6cOGF7f+rUKYKDg/Hy8qJkyZI899xzvP7661SoUIEyZcowZcoUihYtanvyrkqVKjz66KMMHTqU+fPnc/fuXZ599ll69eoV7xN1IiIiGS12CZXiePAlv1p3JFKo1wSMpxFjaKBAyQHZNnD6+eefadGihe39uHHjAOjfvz9Lly5l4sSJhIeH8/TTT3P9+nWaNGnCli1byJs3r+2Y5cuX8+yzz9KqVSvMZjPdunVj7ty56f5ZREREknJ/CZWZtGYtx+wL9RZ3h83WQr0KmFImR+RxyijJyQshIiKSEiFY2M05evNV3GzgsQv11vKFTdZCvS/QiDoUpRElFDSRvO/rbDvjJCIikt3FnmWyYxgwZy+M2/pfod4vu0EBVyrixSyCbDNTn9CRwdSJ9/wSV458qk5ERCSru79Qr01UNIzZAmPvBU3D68L6XlDAmi4ndp26aAyGEUAIlnQefdalwElERCSLsdacO5Jwod4P9lnfz3oE5rW3Feqtg2+cRJhRGJwgNO0HnU3oVp2IiEgWkuDtuUs3ocMKOHDRmpfps67Q/SG7JtNpQWe+tDvWBRPliZsxXOKnGScREZEsIqbmXJyg6cgVaLDQGjQVyg/f94sTNPlTkg5U4hM64oIJUJLLlNCMk4iISBYxh71xa859fwoeXwmWCKjgBd/0ibfm3HK6ATCYOrSlHCcIVZLLFFDgJCIikgndn8wyBAvvstu+0bJgGBIAkdHWQr3rnoAH88c510I62QVIxfFQwJRCCpxEREQymUUcZCgbMLBm9l5AJwqQ57/ZJsOAaT/Aq/dqzvWqBkviL9QbQG86UCl9Bp4DKHASERHJRGLWMcUESQbYF+q9EwVDNsBnv1jfv9QEXmsJZlOcc/WnpoImJ1PgJCIikons5lzcdUwxkijUG6M4BfiaJ6hH8bQcao6kwElERCQTSTCnUiKFeu/3PzooaEojCpxEREQykSuEx914f6HeTU9CDZ94j6+Kt27PpSEFTiIiIhks9hN0hXnAfue6P+DJr/4r1LuxNxSLvxCtCdjCU2k/4BxMgZOIiEgGip0J3IyJksQKit7fE2+h3vgomWX6UOAkIiKSQTZyzO6JuWgMTmOxFuodtxXm3qs5N7wufNDOVnPufv+jHR2opKApHTg1cAoMDGT79u3s2rWLkJAQrl69Sv78+fH29qZ69eo0a9aMDh064Ovr68xuRUREspwerGQNR+PuCL8DT34NG45Z3896BMb7gSluugHreR5iOPXTcKQSm8kwjASfenREeHg4c+fOZcGCBZw5c4aY0+XNmxcvLy9u3bqFxWIhOjoagNy5c9OxY0fGjh1L48aNU/8JMrGwsDA8PDywWCy4u8d/P1pERHKe0WzmA/bF3RG7UK+ri7VQb4+qCZ7nWerzAe3ScKQ5Q3K+r1NV5Hf+/PmUL1+el19+GXd3d1577TW2b9+OxWLh33//JSQkhGvXrnH37l3++OMPli1bRs+ePfn222/x9/fn8ccf59SpU6kZgoiISJYyi13xB01HrkDD2IV6+ycaNAF0o0oajVISkqoZp9y5c9O7d28mTpxItWrVHD7u1q1bLF++nBkzZtC/f39eeeWVlA4hU9OMk4iIxBaChRLMjrvDwUK9sblg4jTPaV2TEyTn+zpVa5yOHDlCxYoVk31cvnz5GDJkCAMHDuTs2bOpGYKIiEimFpNqwI3cvMqPcRs4WKg3Nj1Bl3FSFTilJGiKzcXFhTJlyqTqHCIiIplV7FQDcSSjUC/AcOryMv6cIJTyeCloyiBKRyAiIpIGQrAkHDQlo1AvWBNbvow/xfFQwJTB0iVwOn78OMHBwbbX4cOHCQkJSY+uRURE0lXMrbmFHIw/aHKwUG9s42mkgCmTSHbgdODAAV555RVOnjzJww8/zKxZsyhSpAgAERER/PLLL3ZB0q+//kp4uLXuTsw6dFMCuShERESyskUcZCgb4guXrO4v1Lu6B7Qtn+g5XTAxhgZOH6ukTLICp7/++osWLVrQrFkz3njjDZYsWUKrVq2oXbs2wcHBHD9+nKioKAC7fE6GYVC1alUGDx5M1apVk/UEnoiISGYXgoXdnLPLAh5HMgr1xtAi8MwnWYHTxo0bCQ8P5/PPP8fDw4NWrVrh5eXFsWPHMJvNlC9fnmrVqlGtWjWqV69OtWrVKFeuHLlz58bPz4/nnnsujT6GiIhIxkh0AXiMZBTqjTGbtnTnIQVNmUyyAqeiRYtiGAa7d+/mscceY/fu3YD11tuYMWOYPn06DzzwQBJnERERyR4SXQAeY84eGHuvUO9j5WFl9wQL9cYwY1LQlEklK3N4t27d6NSpEx07dqRcuXI8++yzvP3223h7ezN79mwqVKjAwoULSWUVFxERkSzhOKEJB01R0TDmG3juXtA0vC5s6J1k0ARgJBaISYZKVuBkMplYt24dQUFBzJkzh0OHDjFhwgSOHz/OxIkT+eeffxg2bBg1a9bk22+/Tasxi4iIZApu5I5/R/gd65Nzc++VVnm7NcxrD7kc+9o1gBOEOmeQ4lQpqlVXr149OnTogIeHdQrRzc2NGTNm8Mcff9C9e3d+++03HnvsMR577DF+++03pw5YREQko4Vg4X/soxur4u68dBOaL4MNx6yFeld1h+cbQzKeKHfBRHkSL7kiGSNVRX7vV6pUKVauXMnOnTt5+OGH2bp1K7Vr11b6ARERyTYWcZASzGYkmzlHmP3OmEK9P19wuFAvwDDq4oL1u1JP0mVuqSrym5Tly5czadIkQkJCcHNzY8qUKYwdO5ZcuXJGwnIV+RURyfpiElpWwIuL3KA+C+NveH+h3s19oHzSs0YxxXoBlVPJIMn5vk7TwAng9u3bzJo1i1mzZhEeHk6lSpWYM2cOjzzySFp2mykocBIRydpipxowQcJLtpNZqDfmXDGzS4NJPHO4pK1MFTjFuHTpEi+99BKffvopAJGRkenRbYZS4CQiknWFYKEU7yeeasAwYPqP1hckWagXrGtk9jCEcO5qdimTSM73darXOM2bN4/z588n2c7X15fFixezf/9+/P39U9utiIhImtrNucSDpjtR0H/df0HTpCaw/PEkg6ZP6EQ9itOcMgqasqBUzziZzWZMJhN16tShS5cudOrUierVqztrfFmaZpxERLKmRRxMvHzKP7eg2yoIPG0t1Pu/9jC0boLNTVgL9Y6hgYKlTChdb9UdOHCAdevWsWHDBn799VdMJhOlS5e2BVFNmzbFbHbqw3tZhgInEZGsJwQLJZidcIPT16HdcjjqWKHeYdRlMv4KmDKxDFvjdPr0adauXcuGDRvYuXMn0dHReHl50aFDBzp37kybNm3Inz/hxXLZjQInEZGs5ym+Yjm/xr9z/3nocK9Qb7EC1kK9NX0TPd85xipoyuQyxeLw0NBQNm7cyLp169i2bRvh4eHkzZuXVq1a0bVrVzp06EDhwoXToutMQ4GTiEjWEYKFUXzDOv6Iv8H6P6B38gr1AgTSn+aUcfJoxZkyReAUW0REBNu2bWP9+vVs3LiRy5cvYzabadiwITt37kzr7jOMAicRkaxhFruYyLaEG6SgUC/8l6NJM06ZW3K+r9MlE6WrqysdOnSgQ4cOGIZBUFAQ69evZ8OGRBbeiYiIpIN3EguaoqJh3Nb/as4NqwsftnOo5pwygGdP6ZbHKSfSjJOISOaW6ELw8DvQ52tYf8z6/u3WMKFRojXnhlOXl/FXBvAsJt1mnAYNGpSi40wmE4sWLUpN1yIiIikSU0LFjdxMYnv8jS7dhI5fWGvOubrAZ12TrDlnxsTL956eU8CUfaVqximlaQZMJhNRUVEp7TbL0IyTiEjmsoiDDGVDYmkt4fe/rekGzljgwXywoTc0KpHkuWfxCBNo7LSxSvpJtxmnU6dOpeZwERGRdBOCJfGklpCiQr1mYKaCphwjVYFTqVKlnDUOERGRNBOChV6sSbzRp4dhyAa4Gw2NS8D6XokW6q1OYebymNYy5TDp8lSdiIhIRnmHXTyfWKoBw4BXf4Rp92rOPVEVlnZJtOYcwGb6KGDKgdIkcNq1axdLly4lODiYsLAw3N3dqV27Nv369aNJkyZp0aWIiEgcL7OdN/kp4QZ3omBogHW2CeDFxvBGKzAn/ORcjBOEKnDKgZweOI0dO5a5c+cSs+bcZDJhGAYHDhxg0aJFjBkzhvfee8/Z3YqIiNiZnFTQlMxCvbG5YKI8ia99kuzJqdV3ly1bxpw5c6hQoQLLly/nwoULREZGcvHiRVasWEHFihWZM2cOn376qTO7FRERsfMOu3gjsaDp9HVovNgaNBXIY60552DQZAYltszBnJoAs2HDhly4cIFff/0VD4+4v1AWi4Xq1atTtGhR9uzZ46xuMy2lIxARSV/7CSGAP3mNHYk0Om/N0XTZ8UK9McyY2MNg6lHcSSOWzCDDSq4cOXKEIUOGxBs0AXh4eNCtWzcWLlzozG5FREQYwFqWcTjxRrEL9db0sQZNDhTqhf9KqChoytnS/ak6UyKp6kVERFJiPyFJB01z98JzW6yFeh8tD6scK9QLMIy6TL6XFVxyNqeucapatSpfffUVN2/ejHf/jRs3+Oqrr6haNfG09SIiIkkJwUIgpwjBQgB/JtwwKtoaMI25FzQNqwsBvR0OmgB6UU1BkwBODpyGDRtGSEgIfn5+fPXVV1y9ehWAq1evsmbNGho1akRISAgjRoxwZrciIpLDvMMuSvE+LVlGCWYnvKYp/I71ybk5e63v32ptfXoul+Nff3qCTmJz6q26gQMHcujQIT788EN69uwJWOvZRUdHA2AYBqNGjaJ///7O7FZERHKQWexiYmIJLWPcX6j3067QM+k7HsOpywIOEoVhW9ek2SaJ4dQZJ4C5c+fy448/MmDAAGrVqkXp0qWpVasWAwcO5Mcff2TOnDnO7jJFpk2bhslksntVrlzZtv/27ds888wzPPjgg7i5udGtWzcuX76cgSMWEZEQLLzgSND0+9/QcKE1aHowH3zf36GgyYyJl/HnNM8RSH9O8xyDqeOEkUt2kSaLw5s2bUrTpk3T4tROVbVqVb777jvb+1y5/rscY8eOZdOmTaxevRoPDw+effZZHn/8cXbt2pURQxUREeA4oSSZQyfwFHS9V6i3vBd8k3ShXrDOJHwSa3ZJs0wSnxxdqy5Xrlz4+sbN3WGxWFi0aBErVqygZcuWACxZsoQqVaqwZ88eGjZsGO/5IiIiiIiIsL0PCwtLm4GLiORQ2/kr8Qb3F+pd1wsKJVyoF8AEjKcRY2igYEmSlCaBU1RUFCEhIVy4cIG7d+/G28bf3z8tuk6W48ePU7RoUfLmzYufnx8zZsygZMmSHDhwgLt379K6dWtb28qVK1OyZEmCgoISDJxmzJjB9OnT02v4IiI5SgiWhEuopLBQL8BzNGQWbZw3UMnWnBo4RUdH8+abbzJnzhxCQ0MTbRsVFeXMrpOtQYMGLF26lEqVKnHx4kWmT59O06ZN+e2337h06RJ58uTB09PT7hgfHx8uXbqU4DknTZrEuHHjbO/DwsIoUaJEWn0EEZEc5Sm+jv82XSoK9QL0pprTxijZn1MDp0mTJjFr1iwKFy7MwIEDKVKkiN26oczkscces/25Ro0aNGjQgFKlSrFq1Sry5cuXonO6urri6up4XhAREUlaCBae4mt+5Ezcnddvw+MrU1SoF6A/NZUJXJLFqVHNsmXLqFSpEvv378fNzc2Zp05znp6eVKxYkRMnTvDII49w584drl+/bjfrdPny5XjXRImIiPOEYOE4oVTAi//xc8K3505fh3bL4ehVcMsDa3pA2/IO9dGbhxhLIwVNkmxODZxu3rzJU089leWCJrCO/eTJk/Tt25e6deuSO3dutm/fTrdu3QA4duwYZ8+exc/PL4NHKiKSfS3iIE8TQHRSz879fAE6rEhRod5ZPMIEGjthtJITOTVwqlGjBhcuXHDmKdPMhAkT6NixI6VKleLChQtMnToVFxcXevfujYeHB4MHD2bcuHF4eXnh7u7OqFGj8PPzS3BhuIiIpE4IFseCpvV/wJNfw793rYV6Nz4JxR0r1Pu2giZJJacGTi+//DI9evTg4MGD1KmTuROGhYSE0Lt3b65du4a3tzdNmjRhz549eHt7AzB79mzMZjPdunUjIiKCtm3bMm/evAwetYhI9hSChVUcSTpoSkWh3uHU5XkFTZJKJsMwkswllhyrVq1i1KhRdOrUiZo1a+LuHv+/Avr16+fMbjOlsLAwPDw8sFgsCV4HEZGcLAQLc9jLewQlHjRFRcP4b/+rOfd0Hfgo+TXnTvOccjVJHMn5vnbqjFNERAQBAQFcvXqVRYsWAWAy2T8OahgGJpMpRwROIiKSMIdrzoXfgT5fw/pj1vdvtYbnG4HJsXQDMaIwOEGoAidJFacGTuPGjWP58uXUqFGD7t27Z+p0BCIiknHecTRounyvUO/+5BXqjY8LJsqTdOkVkcQ4NapZvXo1devWJSgoSAGTiIjYiUkz4EZux4Kmo39DuxXWtAMP5oP1vaBxSYf6MmFdCP4i3xGFgQsmPo5Vh04kpZwa3dy+fZsWLVooaBIRETsOpxmIEXgKHl9lTXBZ3gs2PwkVHnTo0JggaTB16EU1ThBKebwUNIlTODXCqVu3LidOnHDmKUVEJItzOM1AjBQU6o3RnNJ8RldbkFQcDwVM4lSOP47ggDfffJMtW7awceNGZ55WRESysOOEOhY0xRTq7b/OGjT1rArf9XM4aAJ4m9YKlCRNOXXGadu2bTRv3pzOnTvTsmXLBNMRmEwmpkyZ4syuRUQkk6rgyILsO1HwdAAsu1eo94XG8KbjhXpBdeckfTg1j5PZ7NgElslkIioqylndZlrK4yQi4kDagfsL9c5rD087VqjXBHSgAlNopqBJUizD8jgFBgY683QiIpLFhWBJPGg6fR3ar4Df/7YW6l3dw5oR3AEmYC9DFDBJunJq4NSsWTNnnk5ERLKg2GkHPubnhBumolCvCVhAJwVNku5SHTjNmzePzp07U6xYMWeMR0REsjCH0w5sOAa9v7IW6q3hYw2aHCzU24fqzNQicMkgqV7jZDabMZlM1KlThy5dutCpUyeqV6/urPFlaVrjJCI5SQgWSvF+0kHTB3thzL1CvW3Lwaoe4J50od7a+LKB3gqYxOmS832d6nQE+/fv56WXXuLOnTtMmTKFWrVqUa5cOcaPH8+PP/5IdHR0arsQEZEsYDfnki7UO3YLjL4XND1dBwJ6OxQ0daUyBxmuoEkynFOfqjt9+jRr165lw4YN7Ny5k+joaLy8vOjQoQOdO3emTZs25M/veD6OrE4zTiKSUyziIEPYkHCDf+9aC/Wu+8P6PhmFek3AWcYqaJI0k5zva6cGTrGFhoayceNG1q1bx7Zt2wgPDydv3ry0atWKrl270qFDBwoXLpwWXWcaCpxEJCcIwUIJZifc4P5Cvcu6wBPVHD7/QjoxmDqpH6hIAjJF4BRbREQE27ZtY/369WzcuJHLly9jNptp2LAhO3fuTOvuM4wCJxHJrkKwsJtznCCUOezhCv/G3zAVhXoB9indgKSDDMvjlBBXV1c6dOhAhw4dMAyDoKAg1q9fz4YNiUzriohIppRkQssYqSjUC9aZJgVNktmky4xTTqUZJxHJTkKw8Do7+JgDSTf+7DAMvleot1EJ60yTgzXnlNhS0lu6zTgNGjQoRceZTCYWLVqUmq5FRCQdLeIgQ9mQdKlew4DXdsDUH6zve1a1rmnK69jXjRn4RDNNkomlasbJ0dp0cTpVrToRkSzD4fxMqSjUawLG04gxNNDTc5Lu0m3G6dSpU6k5XEREMrkQLLzD7qSDpuu3odsq+P5Usgv1+pCfnxmmgEmyhFQFTqVKlXLWOEREJJNJMjdTjDPXrU/OpaBQbwcqEECf1A1UJB2ly1N1IiKStewnxLGgKRWFetspaJIsKM0Cp6ioKK5evUpERES8+0uWdDyPh4iIpJ+YheBJSkWh3pdpyuu0SuVIRdKf0wOnAwcO8NJLL7Fjxw7u3LkTbxuTyURkZKSzuxYRkVQKwcLTBCT99FwKC/WOpQHjaKT1TJJlOTVwCg4OpmnTpuTKlYs2bdoQEBBAzZo18fX15eDBg/z99980b95ca6NERDKp19mRdKHeCd/C+3ut74fWgY/aQW6XJM9txqSgSbI8pwZOr732GgB79+6lSpUqmM1munbtyiuvvMKtW7cYP348a9asYfHixc7sVkREUiEEC8cJ5WuOJp7c8v5CvTNbwcTGDhXqBZhJawVNkuWlLBFTAnbu3EmnTp2oUqWKbVtMmqh8+fLx4YcfUrRoUV566SVndisiIim0iIOU4n1asowP2Zdww8s3oflSa9Dk6gJfdoMXmjgcNAHUo2jqByySwZwaOFksFsqWLWt7nzt3bm7evPlfZ2YzzZs3Z/v27c7sVkREUmA/IQxlQ9I5mo7+DQ0Xwf4L4JUPvusHT1RLVl8umCiPVypGK5I5OPVWXeHChfnnn39s7319fTl+/Lhdm9u3b/PvvwlU0RYRkXThcI6mH05D15UpLtQL1qDpYzrqNp1kC04NnB566CGOHTtme9+4cWPWrVtHUFAQfn5+HD16lFWrVlG5cmVndisiIskQgsWxdAOpLNT7Fo9Qj6KUx0tBk2QbTr1V1759e3bs2MHFixcBeOGFFzAMgyZNmuDt7U316tW5fv261jiJiGSg19mR+M05w4BXf4R+66xBU4+HYHs/h4MmsD5B15tqNKeMgibJVpwaOA0fPpzz58/z4IPWadyaNWuyfft2Hn30UQoVKkTr1q0JCAiga9euzuxWREQcNJntiT85dycKBm2AqT9Y37/QGL7sDnmTd4MiCoMThKZ8oCKZlFNv1eXOnRsfHx+7bY0aNWLTpk3O7EZERFLgZbbzJj8l3OD+Qr0ftYNhD6eoLy0Gl+xKtepERLK5/YTwDJvYz8WEG91fqHdVd3isgkPnNwH9qMnn/EIUhhaDS7bm1Ft1u3btYty4cVy6dCne/RcvXmTcuHHs2bPHmd2KiEgCBrCW+ixMPGj6+YI13cDvf0PRAvDTQIeDpuHU5SxjWUpXTvMcgfTnNM8xmDpO+gQimYvJiMlQ6QTdunXjl19+iZOCILaKFStSu3ZtVq5c6axuM62wsDA8PDywWCy4uztW+FJEJDVCsLCbc1zjX07zD28TlPgBAcegV8oK9QbQmw5UcsKoRTJWcr6vnXqrbv/+/bRqlXi1a39/f7Zt2+bMbkVEBGtupqFsSLpAb4wP91kL9UYbySrUG8ONPCkap0hW5tTA6cqVKxQrVizRNr6+vly5csWZ3YqI5HghWHiaAMeCplQU6o2hxd+SUzk1cPL09OTs2bOJtjlz5gxubm7O7FZEJMc7TmjSpVMg1YV6QZnAJWdzauDUsGFD1q5dy7lz5yhRokSc/WfPnmXdunW0bNnSmd2KiOR4Z7iedKPLN6HTl7DvPORxgU+7JLvm3FSaMYQ6Cpokx3LqU3Xjxo3j33//pXHjxnz66ae2DOIXL15k2bJlNG7cmFu3bjF+/HhndisikiOFYCGQU0xmOwNZn3jjmEK9+85bC/VuT36hXhMoaJIcz6kzTv7+/rz33nuMHz+egQMHAmAymYh5cM9sNjNnzhz8/f2d2a2ISI6TrIXgsQv1lisI3/RJdqFegAV0UtAkOZ5T0xHE+OWXX5g/fz779+/HYrHg6elJ/fr1GT58ONWqJe9fOFmZ0hGISFoIwUJJZjsWNH3+Cwxab60551fcWqjX+4Fk9VcVb7bwlIImybYyLB1BjBo1ajBv3rwE90dFReHi4vjTGyIi8p8AjiUdNBkGvL4DXvnB+r7HQ7CsC+TL7VAfj1OJIrjzKOWVq0kkFqeucfroo4+SbBMVFUWvXr2c2a2ISI4QgoXhBDCSzYk3jCnUGxM0TWxkLdTrYNBkAubQjg9pr6BJ5D5OnXEaPXo0Pj4+dO/ePd790dHR9OrVi6+//tqZ3YqIZDshWDhOKBXwojgejq9pun4buq+C7afAfK9Q73DHC/Wa0FomkcQ4NXBq0qQJffv25cEHH6RFixZ2+6Kjo+nduzdfffUVzz77rDO7FRHJVmaxixfYhgGYMfEM9fiQfUkHTWeuQ/sVcCT5hXoB2lKOhQqaRBLl1Ft1AQEBVKxYka5duxIcHGzbHh0dTZ8+fVi9ejUjR45k7ty5zuxWRCTbeIddTLwXNAFEY/CBI0FTTKHeI8kv1AswhNpsoa+CJpEkODVwcnd3Z+vWrRQsWJDHHnuMv/76C8MwePLJJ1m5ciXDhw/nww8/dGaXIiLZRggWXuC75B8YcAyaLYVLN62FevcOgVq+yTrF09RNfr8iOZBTAyew1qLbunUrUVFRtGnThp49e7Jq1SqGDh2a6JN2IiI5ncNlU2L7cB90WWktpdK2nHWmqXjy0p/0pyb1KJ68fkVyqDRJR1CxYkU2b95My5Yt+frrrxkyZAgff/xxWnQlIpJtuOHYU2+AtVDv89tg9h7r+yG1YV77ZBXqnYo/7amooEkkGVIVOL366quJ7q9fvz7BwcEULVrUrq3JZGLKlCmp6VpEJFuJeWrOIf/ehae+hrX3CvXOaAUvJK9Q70I6MZg6KRipSM6WqszhZnPK7vSZTCaioqJS2m2WoczhIuKIZGUCT2Wh3mHUZTL+WgQuEku6ZQ4PDAxMzeEiIoKDmcAB/rgK7ZbDqevWQr3re0GTkg71URJ3djFYAZNIKqUqcGrWrJmzxiEikqOEYGE35wDYwemkD/jxtHUReEyh3s19oGLShXpzAWvprQzgIk7i9KfqsqOPPvqI0qVLkzdvXho0aMC+ffsyekgikoUt4iAlmM0TrOEJ1vAlvyd+wOe/wCOfWYMmv+IQNNihoAnAwEQtkpeaQEQSpsApCStXrmTcuHFMnTqVgwcPUrNmTdq2bcuVK1cyemgikgWFYGGIo4vADQNe+xH6roW70dZCvdv7gfcDDvcXhcEJQlM4WhG5X6oCp0cffZT9+/en6Njw8HBmzpzpUGHgjPTee+8xdOhQBg4cyEMPPcT8+fPJnz8/ixcvjtM2IiKCsLAwu5eISGwOPzmXykK9MVwwUR6v5A1SRBKUqsDp77//pmHDhrRo0YIlS5ZgsViSPGbPnj08++yzlCpVitdeew0fH5/UDCFN3blzhwMHDtC6dWvbNrPZTOvWrQkKCorTfsaMGXh4eNheJUqUSM/hikgmN5ntbOFk0g2v37YuAl8abC3U+7/28NYj1j8ngxkTH9NRC8JFnChV6QgAli1bxvTp0zl9+jRms5lKlSpRt25dfHx88PT05Pbt24SGhnLs2DF+/vlnbty4gYuLC7169eL111+nZEnHngjJCBcuXKBYsWLs3r0bPz8/2/aJEyfy448/snfvXrv2ERERRERE2N6HhYVRokQJpSMQEV5mO2/yU9INYxfqfSA3rOoB7RyvORfDDOxhiJJbijgg3dIRAPTv359+/fqxefNmlixZwg8//MDnn38ep53ZbKZGjRp07dqVIUOGUKRIkdR2nem4urri6uqa0cMQkUwkBAuvs4OPOZB04wMXoMMX1ppzRQvAxt5Q27G/KxtSjH2cJxrr7bmP6aigSSQNOKXkislkon379rRv3x6Ao0ePEhISwrVr18iXLx/e3t5UrVoVD4+sNV1cqFAhXFxcuHz5st32y5cv4+urp1REJHEx2cAdmtYPOAa9vrJmBa/hA5uedLjm3DnGUhwPQrBwglDK46XbcyJpJE1q1VWpUoUqVaqkxanTVZ48eahbty7bt2+nS5cuAERHR7N9+3aeffbZjB2ciGRqIVh4mgDHgqaP9sHoLRBtQJtysLoHuCd/9ro4HgqYRNJYmgRO2cm4cePo378/Dz/8MPXr1+f9998nPDycgQMHZvTQRCQT68PXRCcVNjmhUC/ACUIVMImkEwVOSXjiiSf4+++/eeWVV7h06RK1atViy5YtmfppQBHJWJPZzg7OJN7ICYV6QekGRNJbqp+qk4SpyK9IzrORY3Tki8QbXQmHjl/8V6h3WRfo5Vih3sYUJ4gQu0Xgg6mT6nGL5GTp+lSdiEhOF4KFTwnmYw5wliQS395fqHfdE9C0lEP9PEBudjJEi8BFMpACJxGRVBjNZj7AwfqVKSzUC9CBCgTQB9AicJGMpMBJRCQFQrDQimX86WgduOW/wMD11ppzfsVhfS+Has5VxZstPKVASSSTUOAkIpJMycrPZBjwxk8wJdD6vvtD8GkXh2rOVeJBfuOZ1AxVRJwsVbXq4hMZGcns2bOpX78+7u7u5Mr1X2wWHBzMyJEj+fPPP53drYhIukhWfqa7UTB4w39B0/ONYKVjhXofpSx/MCpVYxUR53PqjNOtW7do06YNu3fvplChQri7uxMeHm7bX6ZMGZYsWYKXlxevv/66M7sWEUkXxwlNOj8TgOU2dF8N3/1lLc774WMwop7D/SygcypGKSJpxakzTm+++Sa7du1ixowZXLp0iSFDhtjt9/DwoFmzZmzdutWZ3YqIpBs3kp4t4sx1aLzYGjQ9kBsCeicraJpAI61pEsmknDrjtHLlSlq0aMHEiRMBaw27+5UtW5ZDhw45s1sRkTS3nxAmsZ3tnEq8YSoK9YI1N9MYGqRytCKSVpwaOJ09e5auXbsm2qZAgQJYLBZndisikqYGsJZlHE664cY/4Yk11qzg1QtbC/WWcHzmKCahpWabRDIvpwZOBQoU4MqVK4m2OXnyJN7e3s7sVkTE6UKwcJxQznDdsaApFYV6zcCXdMePEgqaRDI5pwZODRs2JCAggOvXr+Pp6Rln/7lz59i8eXOSs1IiIhlpEQd5mgDHFoFHG/D8t/Beygr1xswy9cCxkisikrGcujj8+eef559//qFVq1bs2rWLyMhIAP7991+2b99O27ZtiYyMZNy4cc7sVkTEaUKwMIQNjgVN/96FHqv/C5rebAmfdHQ4aFpFd07znGrNiWQhTp1x8vf358MPP2TMmDH4+/vbthcoUAAAFxcX5s2bR926dZ3ZrYhIqsTclquAF3342rGDroRDpy9g771CvUs7Q+/qyerXmwd0a04ki3F65vARI0bQvHlz5s+fz969ewkNDcXd3Z0GDRowcuRIqlat6uwuRURSLPZtOTMmx2aaUlGoN4YLJsrjlbJBi0iGMRmG4VACXEm+sLAwPDw8sFgsuLu7Z/RwROQ+IVgoxfuOBUsxdpyBLl/CP7ehbEHY/CRUKpSsfs2Y+ISOukUnkkkk5/tatepEJMdyOAt4jOW/wKANcCcKGhaHDY4V6gUwAfNox4Pk19NzIlmYUxeH79q1i3HjxnHp0qV491+8eJFx48axZ88eZ3YrIpIiaznqWEPDgNd3wFNrrUFT94fg+34OB00ABlAZb3pQTUGTSBbm1MDpvffeIyAgAF9f33j3FylShI0bNzJ79mxndisikiwhWBhOAB+wL+nGd6NgSMoK9camNU0i2YNTb9Xt37+fVq1aJdrG39+fbdu2ObNbERGb2E/IxTezs4iDDGWDYzfoUlmoN4YygotkH04NnK5cuUKxYsUSbePr65tkdnERkZS4/wm5+xdgx+RocshZi/XJuSN/Wwv1ruoB7Soke0yzaUt3HlLQJJJNOPVWnaenJ2fPnk20zZkzZ3Bzc3NmtyIihGCxy/YdjcEwAgjhv9qYL/KdYyc7eBEaLLQGTUXc4KeBKQqaXDApaBLJZpxecmXt2rWcO3eOEiVKxNl/9uxZ1q1bR8uWLZ3ZrYhIvE/IRWEQxDkKEcp2/mI5vyZ9oo1/Qq81EJ78Qr2me69odHtOJLtyauA0btw4AgICaNy4Ma+//jqPPPIIRYoU4eLFi3z77bdMnjyZW7duMX78eGd2KyJCBbziJLA0Y6Inaxw/ybz9MOoba/25R8rCmp4OF+o1AQvoRFvKcYJQyiewxkpEsjanJ8CcM2cO48ePJ+a0JpPJ9mez2cz777/PM88848wuMy0lwBRJX4s4yDACiEpOFnBIdaHe2viygd4KlESyqOR8X6dJ5vBffvmF+fPns3//fiwWC56entSvX5/hw4dTrVrOqQCuwEkk/cUsAN/KSccO+Pcu9F0LX9/L6fRmS3ixCZhMDvcZSH+aUyYFoxWRzCDDM4fXqFGDefPmpcWpRUQSdZEbjgdNTijUq/xMIjmLU5+qc3FxoU+fPs48pYhIsvxE4k/22vxxFRoutAZNXvngu74pCpq0AFwkZ3HqjJO7u3u8T9OJiKS1ECzs5hzvsjvpxqko1Ps/2tGBSloALpJDOTVwql+/PocPH3bmKUVEkjSLXUzEwYoEK36FgetTVKjXjIkOVKI4HgqYRHIop96qmzZtGt9//z2ffvqpM08rIhJHCBYCOcVktjsWNMUU6u3ztTVo6lYlWYV6YzKRK2ASydmcOuO0bds2mjdvzsCBA/nggw+oV68ePj4+mO57OsVkMjFlyhRndi0iOUjs0ioOuRsFwzfC4mDr++cbwczW1vpzDjADexhMPYqnaLwikn04NR2B2ezYBJbJZCIqKspZ3WZaSkcg4nwhWCjF+44HTfcX6v3gMRjpeKHemAXgsWveiUj2kmHpCAIDA515OhGROOIrrZKgsxZovwJ+u2It1LuyO7SvmORh5SnICroRzl0tABcRO04NnJo1a+bM04mI2IRg4Tihjj01B9ZCve1XwKWb1kK9m56E2kUcOjSQAQqWRCReaZIAU0TEmZK9pil2od5qha3pBhws1DuLRxQ0iUiC0iRw2rVrF0uXLiU4OJiwsDDc3d2pXbs2/fr1o0mTJmnRpYhkUyFYkhc03V+od3UP8Mjr0KFv8wgTaJyK0YpIduf0wGns2LHMnTs3TpHfAwcOsGjRIsaMGcN7773n7G5FJJtyeE1TtAETt8G7Qdb3g2vD/xwv1LuPIXpqTkSS5NQ8TsuWLWPOnDlUqFCB5cuXc+HCBSIjI7l48SIrVqygYsWKzJkzR3meRMQh+wlhPX8k3fDWXei5+r+g6Y2WsKCjw0HTQjopaBIRhzg1HUHDhg25cOECv/76Kx4ecdcIWCwWqlevTtGiRdmzZ4+zus20lI5AJOV6sorV/J50wyvh0PlL2BOSokK9q+hOD6qlYqQiktUl5/vaqTNOR44coVu3bvEGTQAeHh5069aNI0eOOLNbEclmRrHZsaDp2L1CvXtCoGDeZBfqNQN+qL6miDgu3Z+quz+LuIhIbO+wiw/Zl3TDVBTqjfEJnfQEnYgki1NnnKpWrcpXX33FzZs3491/48YNvvrqK6pWrerMbkUkmwjBwvOO1J1b8Ss88pk1aGpYHPYMTlbQZMbEPoYoG7iIJJtTA6dhw4YREhKCn58fX331FVevXgXg6tWrrFmzhkaNGhESEsKIESOc2a2IZBND2ZB4A8OAN1JeqBesJVQ+oaMWg4tIijj1Vt3AgQM5dOgQH374IT179gSs9euio6MBMAyDUaNG0b9/f2d2KyLZQA9WsYWTCTe4v1DvBD946xGHCvWagEk05RHKqoSKiKSKU5+qi/HTTz/FmwCzf//+NG3a1NndZVp6qk4kcTFlVMK5Q0e+SLih5Tb0WA3bkleodwmdKY2ngiURSVSGFfmN0bRp0xwVIIlI8jlcRiWFhXqfojoDqO2k0YqIWKU6cAoLCyNv3rzkyZPHGeMRkRzA4TIqBy9ChxVw8V6h3o1PQh3HCvXOoLUTRioiYi/Vi8MLFizIW2+9Zbdt7969zJ07N7WnFpFsJgQLq/iNEWxKOmja9Cf4L7EGTdUKw54hDgdNL9FUt+ZEJE2kesbJMAzuXya1ZcsWXn31VUaPHp3a04tIFrefEH7iLKHc4k1+cqxUbyoK9banAm/QKlVjFhFJSLonwBSRnGMAa1nGYccPiDbghW3wzr2ac4NqwfwODtece4mmCppEJE0pcBKRNLGfkOQFTbfuQt+18NVR6/vXW8BLTcGBagNPUZ0ZtNbtORFJcwqcRCRNBPCn443vL9S7pDM86VjNue48xGd0S+EoRUSSR4GTiDjdIg7yGjsca3zsKrRbAX/9Yy3Uu64X+JdK8jATsIHedKBS6gYrIpIMTgmcPv/8c/bs2WN7f+LECQDatWsXb3uTycSmTZuc0bWIZCIhWNjNuaRLp8RIYaFeF0x8TEcFTSKS7lKdOdxsTn5GA5PJRFRUVGq6zRKUOVxyEocTWsZY8SsMXG+tOdegGGzoDYUTrzn3An48SsUkM4HHZCSvoIzhIuKAdM0cfurUqdSeQkSyOIcTWoK1UO+MnfDy99b33arAZ10hX+4kD+1G1SSL88YO4Mz3CvoOpo4jH0NEJEmpDpxKlUp6LUJmVLp0ac6cOWO3bcaMGbz44ou297/88gvPPPMM+/fvx9vbm1GjRjFx4sT0HqpIpnecUMeCprtRMGITLDpkfZ+MQr0A4dxNdP/9AVw0BsMIoC3lNPMkIk6RoxeHv/rqqwwdOtT2vkCBArY/h4WF0aZNG1q3bs38+fP59ddfGTRoEJ6enjz99NMZMVyRTOtnLiTdKIWFemO4YKI8Xom2iS+Ai8LgBKEKnETEKXJ04FSgQAF8fX3j3bd8+XLu3LnD4sWLyZMnD1WrViU4OJj33nsvwcApIiKCiIgI2/uwsLA0GbdIZhKChRfYlnij+wv1ftkdOiRdqNcEGPy3GDyp4KcCXpgx2QVPjgRcIiKOSnWtuqxs5syZPPjgg9SuXZtZs2YRGRlp2xcUFIS/v79d8eK2bdty7Ngx/vnnn3jPN2PGDDw8PGyvEiVKpPlnEMlIIVh4h92J36Q7eBEaLrQGTUXcYMfARIOmfORiFd05x1jOMpZA+nOa5xxap1QcDz6hIy5Yb/05GnCJiDgqx844jR49mjp16uDl5cXu3buZNGkSFy9e5L333gPg0qVLlClTxu4YHx8f276CBQvGOeekSZMYN26c7X1YWJiCJ8ny4ntCbT8hvMNuVvN74kHTpj/hiTUQftdaqHfTk1Ay8SDmT0bZBTrJDXoGU4e2lOMEoUk+fSciklzZKnB68cUXeeuttxJtc/ToUSpXrmwX4NSoUYM8efIwbNgwZsyYgaura4r6d3V1TfGxIplRfE+o/cQZx0qpxC7U27osrEm6UO8EGjkl0CmOhwImEUkT2SpwGj9+PAMGDEi0TdmyZePd3qBBAyIjIzl9+jSVKlXC19eXy5cv27WJeZ/QuiiR7CS+J9SGOJLYMhWFesfQIBUjFhFJe9kqcPL29sbb2ztFxwYHB2M2mylcuDAAfn5+vPzyy9y9e5fcua35ZbZt20alSpXivU0nkt04nGIgtlQU6h1GXc0SiUimlyMXhwcFBfH+++9z+PBh/vrrL5YvX87YsWN56qmnbEHRk08+SZ48eRg8eDBHjhxh5cqVzJkzx+4Wn0h2FvOEmsP+DoeWn1qDpjwusPxxeNnfoaDJBEzGP+WDFRFJJ6macRo0aFCKjjOZTCxatCg1XaeKq6srX375JdOmTSMiIoIyZcowduxYu6DIw8ODb7/9lmeeeYa6detSqFAhXnnlFeVwkhyjOB68RWueTyrVAKS4UC9Y//X2CZ002yQiWUKqatUlVKfOZDIR32ljtqtWnUjmF4KFTzjAa+xIvOFPZ6DzvUK9ZTzhmz5JFup9k5b0paaefBORTCHdatXdX6cuOjqaMWPGsGfPHsaMGUPTpk3x8fHh8uXL7Nixg7lz5+Ln58fs2bNT062IpLFFHGQoG5Je4ZSCQr0umOhLTT35JiJZUqoCp/vr1M2cOZO9e/dy+PBhihQpYtteqVIl/P39GThwILVr12bNmjWq+SaSScU8TZdo0HR/od7Hq8DnSRfqNYESUopIlubUxeGLFi2iZ8+edkFTbMWKFaNnz54sWLDAmd2KiJOEYGEEmxJ/mu5uFAwN+C9oGu8Hq3skGTQB7GWIQxnARUQyK6emIwgJCSFv3sQT3OXNm5eQkBBndisiTvAOu5JeCH5/od65j8Iz9ZM8twlYQCfqUdw5gxURySCpWhx+vwoVKmAYBr/99lu8AdS///5L9erVMZvNHD9+3FndZlpaHC6ZWexSKl/wGxOTCprO3SvU++sVyJ8bViZdqPcpqtOJSvhRQrfnRCTTSs73tVNv1Q0ZMoS//vqLxo0bs379eq5duwbAtWvXWLduHU2aNOH06dMMHTrUmd2KSDIt4iCleJ+WLKMU7ycdNB26CA0WWoMmXzfYMSDRoKkKhTjHWD6jGz2opqBJRLINp844RUdHM3ToUJYsWYLpXtI7s9lMdHQ0AIZhMHDgQBYuXGjbn51pxkkyoxAslOJ9x7OCbz4OPVdbC/VW9YbNfZIs1HuOsQqWRCTLSLd0BPczm80sWrSIfv36sWzZMn755RcsFgseHh7UrFmTvn370rx5c2d2KSLJlKxSKv/bD88mr1DvLB5R0CQi2Vaa1Kpr1qwZzZo1S4tTi0gqxZRSSTR4ur9Q78Ba8LFjhXofpqhzBioikgnlyFp1IjlZcTx4lHIJN7h1F55Y81/Q9HoLWNTJoaDJDJTHyzkDFRHJhJweOEVGRjJ79mzq16+Pu7s7uXL9N6kVHBzMyJEj+fPPP53drYg46B12sZkT8e+MKdS75ndrod7PuyarUK9qzolIdufUW3W3bt2iTZs27N69m0KFCuHu7k54eLhtf5kyZViyZAleXl68/vrrzuxaRBKwnxB+4ixNKQmQcK6mP6/BY8v/K9S79gloVjrJ85uAp6nLZPwVNIlItufUGac333yTXbt2MWPGDC5dusSQIUPs9nt4eNCsWTO2bt3qzG5FJAEDWEt9FjKeb6nPQuqzMP6GP50Bv0XWoKmMJ+wenGTQZAIm0IizjGW+yqiISA7h1BmnlStX0qJFC1sduvhSDpQtW5ZDhw45s1sRicd+QljG4aQbfvErDEheod5VdFdSSxHJkZw643T27FkefvjhRNsUKFAAi8XizG5FJB4/cTbxBoYBM36CJ7+2Bk1dK8P3/ZMMmhbSSUktRSTHcuqMU4ECBbhy5UqibU6ePIm3t7czuxWR+4Rg4TZ3E25wNwpGbIJF92Z/xzWEtx8Bl8T/LbWK7vSgmhNHKiKStTg1cGrYsCEBAQFcv34dT0/POPvPnTvH5s2b6dq1qzO7FcnxYurOuZGbRRziEw4knKUpLAK6r0p2oV4z4EcJZw5bRCTLcWrg9Pzzz9OiRQtatWrF3LlziYyMBKzFfYOCghg1ahSRkZGMGzfOmd2K5GiLOMjTBDiWDTwFhXpjzFRGcBER5wZO/v7+fPjhh4wZMwZ/f3/b9gIFCgDg4uLCvHnzqFu3rjO7FcmxQrAwlA2OFVA5dBE6fAEXblgL9W7sDXWTzvJtAt7mESbQOLXDFRHJ8pxecmXEiBE0b96c+fPns3fvXkJDQ3F3d6dBgwaMHDmSqlWrOrtLkRxrDnsdC5pSUKg3xgZ604FKqRqniEh24dTA6ezZs3h6elKlShXmzJkTb5sbN27wzz//ULJkSWd2LZLjhGDhPYKSbjj/Z3hmc7IK9cbmRp5UjFJEJHtxajqCMmXKJBgwxZg7dy5lypRxZrciOdJuziVdqHfiNuvTc9GGtVDv5icTDJoaUoz7M6+5YFLtORGRWJwaOBmGgWEkfuMgqf0ikrRFHKQXaxJuEFOod9Zu6/vXEi/UO4r6BDGUBXTC5V745IKJj5URXETEjtPXOCUlJCTEtlhcRJJvPyE8TUDCc01/h0PnLyEoxFqod3En6FMjwfP1oTpzaQfAYOrQlnKcIJTyeCloEhG5T6oDp1dffdXu/Q8//BBvu6ioKM6dO8eXX35Jw4YNU9utSI60iIOJP0X35zVotxxOOl6odyat7d4Xx0MBk4hIAkxGKu+dmc3/3e0zmUxJ3oorWrQoa9eupV69eqnpNksICwvDw8MDi8WCu7t7Rg9Hsrj9hCRcpBeshXq7rITQW9ZCvZv7QOVCCTY3AQvoxGDqOH2sIiJZSXK+r1M94xQYGAhY1y61bNmSAQMG0L9//zjtXFxc8PLyonLlynbBlogkLWamKUHJKNT7FNXpRCUV6RURSYFUB07NmjWz/Xnq1Kk0b97cbpuIpE4IFoYkFDQZBszcCS99b33ftTJ8/rg1K3g89jGEehRPo5GKiGR/Tl0cPnXqVGeeTkSwJrmM190oGLkJFjpWqPdlmipoEhFJJafeM9u9ezfjxo3j0qVL8e6/ePEi48aNY8+ePc7sViTbCsHCO+yOuyMswlo+ZeEha6HeDx+Dd9smGDQ1pBiv0yqNRysikv05NXB69913CQgIwNfXN979RYoUYePGjcyePduZ3YpkSwkGTecs0GQxfHvSektufS94pn6i51pNzzQapYhIzuLUW3X79++nVavE/1Xr7+/Ptm3bnNmtSLaziIPxr2sKvgTtVzhcqDfmyTktAhcRcQ6nBk5XrlyhWLFiibbx9fXlypUrzuxWJFtJcDH45uPWbOA371gL9W56Ekp5JnouFegVEXEupwZOnp6enD17NtE2Z86cwc3NzZndimQbIViYwNa4O2IX6m1VBr7q6VChXhXoFRFxLqeucWrYsCFr167l3Llz8e4/e/Ys69ato1GjRs7sViRbWMRBSjCblfz+38b7C/UOqGVNbOlA0KQCvSIizufUwGncuHH8+++/NG7cmE8//ZSLFy8C1qfpli1bRuPGjbl16xbjx493ZrcimVIIFgI5RQiWJNtu5Fjc23O37kKv+wr1Lu5krT8Xj+HUVYFeEZE0luqSK/ebM2cO48ePt5VeiV2GxWw28/777/PMM884s8tMSyVXcq5FHORpAojGwIyJT+iYYGmTAaxlGYftN8Yu1JvbDIs7w1MJF+o1A2cYC6ACvSIiyZSc72unB04Av/zyC/Pnz2f//v1YLBY8PT2pX78+w4cPp1q1as7uLtNS4JQzhWChFO8THasUrwsmTvOcXTATgoU32cH/OGB/gtiFej3zwrqkC/UuVM05EZEUS9dadfGpUaMG8+bNS4tTi2R6xwm1C5oAojA4QagtcEow3cDOs9aZpphCvZuehCreCfb1FNWZQWvNLomIpJM0CZxEcrIKeGHGFGfGKWahdoLpBr78DfqvsxbqrV8MAuIv1GsChlGXl/FXwCQiks5SFTgNGjQIk8nEm2++iY+PD4MGDXLoOJPJxKJFi1LTtUimVRwPPqEjwwggCiPOQu0+fG1/gGHAW7tg0nbr+0QK9balHAuV0FJEJMOkao2T2WzGZDJx9OhRKlasiNns2EN6JpOJqKiolHabZWiNU84WgiXOQu3JbOcNfvqv0f2Fesc2hFkJF+rdxxAV6hURcbJ0W+N06tQpAFu28Jj3ImKdebp/Mbhd0BQWAT1WW2vOmU0w51F4NvGac7s4p8BJRCQDpSpwKlWqVKLvRcQqBAufxH56LiTM+uTcr1est+S+7AYdky6N0pgSaThKERFJihaHi6SRECwcJ5SfucCLfPffYvFkFuqN0Z+amm0SEclgCpxE0kDsBJh2vjkOPR0r1GvCWqT3BKE0poSCJhGRTCDVT9WlhJ6qk+xsPyEMZcP9IRN8fK9Qb5QBLe8V6vWMv+acCVhAJzqQ9O07ERFJP6l+qi7ek8YqsxLfdj1VJ9lVvIktow2Y9B28fa/m3IBa8HGHeGvOmYDxNGIMDZRyQEQknaT7U3UxoqOjGTNmDHv27GHMmDE0bdoUHx8fLl++zI4dO5g7dy5+fn7Mnj07Nd2KZEohWBgaX6He/utg9e/W9682h8n+YDLFOf5/tKMDlRQwiYhkYk59qm7mzJns3buXw4cPU6RIEdv2SpUq4e/vz8CBA6lduzZr1qxh4sSJqelaJNPZzTn723NX/7WWT9l9LslCvbN4hOEknopAREQynmMZKx20aNEievbsaRc0xVasWDF69uzJggULnNmtSIZ7h108wZr/Nhy/Bn6LrEGTZ174tm+CQVMfqjOBxuk0UhERSQ2nPlUXEhJC3rzxL3aNkTdvXkJCQpzZrUiGiEk38B1/8WbsxJaxC/WW9oTNCRfqNQEzaZ0u4xURkdRz6oxT8eLFWbt2Lbdv3453/7///svatWspXlyPVUvWtoiDlOJ9WrLMPmha+Ru0+tQaNNUvBnsG2wVNT1Hd9j+dCyYWqO6ciEiW4tTAaciQIfz11180btyY9evXc+3aNQCuXbvGunXraNKkCadPn2bo0KHO7FYkXYVgiZujyTBg5k7o9RXcibIW6g3sDz5udscOpg5nGEsg/TnNcwymTjqPXkREUsOpt+qef/55/vzzT5YsWcLjjz8OWFMWREdHA2AYBgMHDuT55593Zrci6SYEC6s4Yh803Y2y5mdacND6PoFCvS6YbAV/NcskIpI1OTVwMpvNLFq0iH79+rFs2TJ++eUXLBYLHh4e1KxZk759+9K8eXNndimSbhZxMG5iy7AI6LkatiZeqNcFEx/TUQGTiEgWl6oEmJnVG2+8waZNmwgODiZPnjxcv349TpuzZ88yYsQIAgMDcXNzo3///syYMYNcuf6LJX/44QfGjRvHkSNHKFGiBJMnT2bAgAEOj0MJMLOPECyU4L78YyFh1ppzv1yOt1CvCXiLR6hHUdtMk4iIZD7plgAzs7pz5w49evTAz88v3tIuUVFRtG/fHl9fX3bv3s3Fixfp168fuXPn5s033wSsyT3bt2/P8OHDWb58Odu3b2fIkCEUKVKEtm3bpvdHkgwWwDH7DQ4U6t1Ab5VMERHJZpy6OBwgMjKS2bNnU79+fdzd3e1mcIKDgxk5ciR//vmns7u1M336dMaOHUv16tXj3f/tt9/y+++/8/nnn1OrVi0ee+wxXnvtNT766CPu3LkDwPz58ylTpgzvvvsuVapU4dlnn6V79+6JZj2PiIggLCzM7iVZWwgWAjnFMa79t/Gb49B0iTVoquptfXLuvqAJwI086ThSERFJD04NnG7dukWLFi2YMGECZ86cwd3d3a5mXZkyZViyZAmffvqpM7tNtqCgIKpXr46Pj49tW9u2bQkLC+PIkSO2Nq1b2+fXadu2LUFBQQmed8aMGXh4eNheJUqUSJsPIOkidsqBOey1bvz4Z+j4Bdy8Yy3Uu3MQlPKMc2zMQnAREclenBo4vfnmm+zatYsZM2Zw6dIlhgwZYrffw8ODZs2asXXrVmd2m2yXLl2yC5oA2/tLly4l2iYsLIxbt27Fe95JkyZhsVhsr3PnzqXB6CU9xEk5EG3AC9tg+CaIMqyFer/pY80Kfh8tBBcRyb6cGjitXLmSFi1aMHHiREwmE6Z4CpmWLVuWs2fPJvvcL774ou2cCb3++OMPZ3yMFHN1dcXd3d3uJVnTcUL/C5pu3YVea+Dt3db3rzaHxZ0gj4vdMWZgFd2Vn0lEJBtz6uLws2fP0rVr10TbFChQAIvFkuxzjx8/Pskn2sqWLevQuXx9fdm3b5/dtsuXL9v2xfw3ZlvsNu7u7uTLl8/BUUtWE1NGxY3cmDERfTXcoUK9ZuATOtGDauk/aBERSTdODZwKFCjAlStXEm1z8uRJvL3jr9uVGG9v7xQdFx8/Pz/eeOMNrly5QuHChQHYtm0b7u7uPPTQQ7Y2mzdvtjtu27Zt+Pn5OWUMkvm8wy5e4DuiMTBjospxE0faLYITodZbcmufgOal4xw3jLpMxl+35kREcgCn3qpr2LAhAQEB8eZNAjh37hybN2/G39/fmd3GcfbsWYKDgzl79ixRUVEEBwcTHBzMzZs3AWjTpg0PPfQQffv25fDhw2zdupXJkyfzzDPP4OrqCsDw4cP566+/mDhxIn/88Qfz5s1j1apVjB07Nk3HLhljMtt5nm2223PRO89wxG+mNWgq7Qm7B0Hz0piw5mcCMGNiFo8wX+uZRERyDsOJfvzxR8NsNht16tQxdu7caUyePNkwm81GeHi48d133xlVqlQxcufObfz888/O7DaO/v37G0CcV2BgoK3N6dOnjccee8zIly+fUahQIWP8+PHG3bt37c4TGBho1KpVy8iTJ49RtmxZY8mSJckah8ViMQDDYrE44VNJWjhnXDeeNjYYGFP/e33ZzSCPi/X3pn4xg0vjbftWGb8a54zrRqDxl3HOuJ7RwxcRESdIzve10zOH/+9//2PMmDFERUXF2efi4sK8efPiPG2XXSlzeOa2iIP2T84ZBry9C17cbn3fpTIsf9yaFRzr03KneU6zSyIi2UyGZg4fMWIEzZs3Z/78+ezdu5fQ0FDc3d1p0KABI0eOpGrVqs7uUiTZ4qQbuL9Q73MN4J02tkK9SjEgIiKQRiVXqlSpwpw5c9Li1CIpEvO0XIV7NePs0g3cX6j3/bYwqgFgXQT4Jd3xo4SCJhERcW7g5OLiQq9evVi+fLkzTyuSKrFvyZkx8QkdaUs5a7qBEIt9od4vukEna325mFkmpRgQEZEYTg2c3N3dVWZEMpX7b8lFYzCMAGbQmujgi/8V6vV5ADY+CQ8X1SyTiIgkyKmBU/369Tl8+LAzTymSKna35O6JwmDiN/Og5xprzbmHvGHzk1DKU7NMIiKSKKfmcZo2bRrff/99hhfxFYlRAS/M3Ff655MD9oV6d1kL9c6mrcqliIhIopw647Rt2zaaN2/OwIED+eCDD6hXrx4+Pj5xataZTCamTJnizK5F4iwAByiOB5/QkWEEEBUdDZO++6/mXP+a8ElHyOOCCya685BuzYmISKKcmsfJbHZsAstkMsWb5ym7UR6n9BPfAvDYM0ef3z5A3379YPXv1g2vNofJ/nAvqH+bR3iexhkwchERyWgZlscpMDDQmacTcUhCC8DbUo7ieHD16lXmdH4Gdv9uLdS7qBP0rWl3jnoUzYihi4hIFuPUwKlZs2bOPJ2IQxJaAH6CUG4dv0K7du04ceIEeTwf4M7a7nEK9bpgojxe6ThiERHJqpyyODwoKIiWLVtSoEAB3N3deeSRR9i3b58zTi2SpPgWgJuBHbt20sCvISdOnKBE6ZLc3T0g3qBJGcFFRMRRqV7j9Ouvv9KgQQNu375ttz1fvnzs27cvR5dY0Rqn9LOIg9YF4BiYAGPlb9B/HUREUbpeVd4JWEx3n81xjltFd6UeEBHJ4ZLzfZ3qGaeZM2dy+/ZtXn75ZS5dusSlS5eYMmUKt27d4q233krt6UUc0pZyrKAb84zH4K1d0OsriIiCLpU5+0NnSvoUjTMr5YIJP5SwVUREHJfqGaeSJUtSunRpduzYYbe9WbNmnD59mjNnzqRqgFmZZpzSh+2JusgoeGYTfBK3UG8g/TnJP7ZZqZhbdMrZJCIi6fpU3eXLl+nVq1ec7Q0aNGDv3r2pPb1IvGJyNrmR2xo03bhtzQS+5QSYgPcfhdHWQr0xi7+bU4a2lOMEoZSPletJRETEUakOnO7evYubm1uc7Q888AB3795N7elF4rg/Z1N0iAU6rIDD/xXqNXeqTHSsmaXYCTEVMImISEo5NR2BSFqLk7MpnkK9Lg8XI4jBhHNXM0siIuJUTgmcPv/8c/bs2WO37cSJEwC0a9cuTnuTycSmTZuc0bXkMHY5m7acgB6rrTXnqhSCzX1wKV2Qj+lIPYpn7EBFRCRbckrgdOLECVugdL8tW7bE2XZ/7ToRR8XkbIr+5GcYuQmiDGhZhu1fBWD2zK8ZJhERSVOpDpxOnTrljHGIOKRodAEeeukwv7210bqhf02e+uQlWubJufnCREQk/aQ6cCpVqpQzxiGSpNu3b9Oj/5P8tmqtdcP05jDFny9MR5mBRTNNIiKS5rQ4XLKEq1ev0qVLF3bt2hWnUG9MXToFTiIiktYUOEmmd/z4cVuhXncPd26s7YrRorRtv4r0iohIenFKkV8RZwnBQiCnCMECwK5du/Dz8+PEiROULl2aPUF7WNBiNC73yqeoSK+IiKQnzThJpnF/Ysuhq1xZ2m8aERER1KtXj4CAAHx8fKgCygAuIiIZQoGTZIiYkikV7gU+doktDYPot3fy8YvbAejcuTMrVqwgf/78tuOVAVxERDKCAidJd/fPLH1CR8pS0Bo0RUbbFert/txAvnxnAS4uLhk8ahEREa1xknQWp2QKBsMIwI3cmG7cgY5fWIMmE5jmPMrs2bMVNImISKahGSdJV3YlU+6JwuB0yFmKd/iKc4dPQL5cmL/oziedn9ftOBERyVQUOEm6spVMiRU8mQ9fZnT7Hlw6fwFvn8K8GvAxHeq1UNAkIiKZjm7VSboqjgef0NGWTsC85QS5m3zKpfMXqFKlCvv27GV4vS4KmkREJFNS4CTpbjB1OM1zjPskD6YOXxJx819atGjB7t27KV26dEYPT0REJEEKnCTdRUdH8+GLM3hv2MtERUXRr18/tmzZgqenZ0YPTUREJFFa4yTp6vbt2/Tv359Vq1YBMH36dKZMmYLJZMrgkYmIiCRNgZOkm9iFenPnzs3ChQvp169fRg9LRETEYQqcJF3ELtTr4eHB2rVradGiRUYPS0REJFkUOEma27VrF507d+batWuUKlWKzZs389BDD2X0sERERJJNi8MlTa1atYpWrVpx7do1Hn74Yfbs2aOgSUREsiwFTpImDMPg7bff5oknniAiIoLOnTvzww8/4Ovrm9FDExERSTEFTuJ0kZGRjBgxghdeeAGAMWPG8NVXX/HAAw9k8MhERERSR2ucxKlu3LhBz5492bJlCyaTidmzZzNmzJiMHpaIiIhTKHASpzl//jzt27fn8OHD5MuXjy+++ILOnTtn9LBEREScRoGTOMXhw4dp374958+fx8fHh4CAAOrVq5fRwxIREXEqrXGSVNu6dStNmjTh/PnzVKlShT179ihoEhGRbEmBk6TKJ598Qvv27bl58yYtWrRg165dKtQrIiLZlgInSZHo6GgmTZrEsGHD7Ar1FixYMKOHJiIikma0xkmS7fbt2wwYMICVK1cCMG3aNF555RUV6hURkWxPgZMky/2FehcsWED//v0zelgiIiLpQoGTOOzEiRO0a9eO48eP4+Hhwddff03Lli0zelgiIiLpRoGTOGT37t106tRJhXpFRCRH0+JwSdLq1atp2bKlCvWKiEiOp8BJEhRTqLdnz54q1CsiIoICJ0lAZGQkI0eOtBXqHT16tAr1iohIjqc1ThLHjRs3eOKJJ/jmm29UqFdERCQWBU5iR4V6RUREEqbASWx++eUX2rVrx/nz5ylcuDAbN25UzTkREZFYsuUapzfeeINGjRqRP39+PD09421jMpnivL788ku7Nj/88AN16tTB1dWV8uXLs3Tp0rQffAa5v1Dv3r17FTSJiIjcJ1sGTnfu3KFHjx6MGDEi0XZLlizh4sWLtleXLl1s+06dOkX79u1p0aIFwcHBPPfccwwZMoStW7em8ejT34IFC2jfvj03btygefPmKtQrIiKSgGx5q2769OkASc4QeXp6Jvho/fz58ylTpgzvvvsuAFWqVGHnzp3Mnj2btm3bxntMREQEERERtvdhYWEpGH36iY6OZvLkycyYMQOAvn37snDhQvLkyZPBIxMREcmcsuWMk6OeeeYZChUqRP369Vm8eDGGYdj2BQUF0bp1a7v2bdu2JSgoKMHzzZgxAw8PD9urRIkSaTb21Lp9+zZPPvmkLWiaNm0ay5YtU9AkIiKSiGw54+SIV199lZYtW5I/f36+/fZbRo4cyc2bNxk9ejQAly5dwsfHx+4YHx8fwsLCuHXrFvny5YtzzkmTJjFu3Djb+7CwsEwZPF27do3OnTuza9cucuXKxcKFC1WoV0RExAFZJnB68cUXeeuttxJtc/ToUSpXruzQ+aZMmWL7c+3atQkPD2fWrFm2wCklXF1dcXV1TfHx6UGFekVERFIuywRO48ePZ8CAAYm2KVu2bIrP36BBA1577TUiIiJwdXXF19eXy5cv27W5fPky7u7u8c42ZQUq1CsiIpI6WSZw8vb2xtvbO83OHxwcTMGCBW0zRn5+fmzevNmuzbZt2/Dz80uzMaSl1atX07dvXyIiInj44YcJCAhQzTkREZFkyjKBU3KcPXuW0NBQzp49S1RUFMHBwQCUL18eNzc3AgICuHz5Mg0bNiRv3rxs27aNN998kwkTJtjOMXz4cD788EMmTpzIoEGD+P7771m1ahWbNm3KoE+VMoZhMGvWLFvNuU6dOrFixQrVnBMREUkJIxvq37+/AcR5BQYGGoZhGN98841Rq1Ytw83NzXjggQeMmjVrGvPnzzeioqLszhMYGGjUqlXLyJMnj1G2bFljyZIlyRqHxWIxAMNisTjpkyXP3bt3jeHDh9s+/+jRo43IyMgMGYuIiEhmlZzva5NhxHoGX5wqLCwMDw8PLBYL7u7u6dq3CvWKiIg4Jjnf19nyVl1Od/78eTp06EBwcDD58uVjxYoVdlnRRUREJGUUOGUzKtQrIiKSdnJ05vDs5v5CvXv27FHQJCIi4kQKnLKJ+Ar1lilTJqOHJSIikq0ocMrioqOjeemll3j66aeJioqib9++bN26lYIFC2b00ERERLIdrXHKokKwcOT2ReYNnMyGL78CYOrUqUydOhWTyZTBoxMREcmeFDhlQYs4yNBrKzG6fAk7z+KSy4VFCxepUK+IiEgaU+CUxYRgYeiJpRjtlsPxUPBwxfj6CVq17JLRQxMREcn2tMYpizlOKMZH+6xBU0kP2DWI6JZlOEFoRg9NREQk29OMUxZTAS9Mb7fBMIAXm4CvGy6YKI9XRg9NREQk21PglMUUx4MFubsw7H0XojBwwcTHdKQ4Hhk9NBERkWxPgVMWNJg6tKUcJwilPF4KmkRERNKJAqcsqjgeCphERETSmRaHi4iIiDhIgZOIiIiIgxQ4iYiIiDhIgZOIiIiIgxQ4iYiIiDhIgZOIiIiIgxQ4iYiIiDhIgZOIiIiIgxQ4iYiIiDhIgZOIiIiIgxQ4iYiIiDhIgZOIiIiIgxQ4iYiIiDhIgZOIiIiIg3Jl9ACyM8MwAAgLC8vgkYiIiEhCYr6nY763E6PAKQ3duHEDgBIlSmTwSERERCQpN27cwMPDI9E2JsOR8EpSJDo6mgsXLlCgQAFMJlNGDydBYWFhlChRgnPnzuHu7p7Rw8kSdM2ST9cs+XTNkk/XLPl0zawzTTdu3KBo0aKYzYmvYtKMUxoym80UL148o4fhMHd39xz7P01K6Zoln65Z8umaJZ+uWfLl9GuW1ExTDC0OFxEREXGQAicRERERBylwElxdXZk6dSqurq4ZPZQsQ9cs+XTNkk/XLPl0zZJP1yx5tDhcRERExEGacRIRERFxkAInEREREQcpcBIRERFxkAInEREREQcpcMpB3njjDRo1akT+/Pnx9PSMt43JZIrz+vLLL+3a/PDDD9SpUwdXV1fKly/P0qVL037wGcSRa3b27Fnat29P/vz5KVy4MM8//zyRkZF2bXLSNYtP6dKl4/xezZw5067NL7/8QtOmTcmbNy8lSpTg7bffzqDRZh4fffQRpUuXJm/evDRo0IB9+/Zl9JAyhWnTpsX5fapcubJt/+3bt3nmmWd48MEHcXNzo1u3bly+fDkDR5wxduzYQceOHSlatCgmk4l169bZ7TcMg1deeYUiRYqQL18+WrduzfHjx+3ahIaG0qdPH9zd3fH09GTw4MHcvHkzHT9F5qPAKQe5c+cOPXr0YMSIEYm2W7JkCRcvXrS9unTpYtt36tQp2rdvT4sWLQgODua5555jyJAhbN26NY1HnzGSumZRUVG0b9+eO3fusHv3bpYtW8bSpUt55ZVXbG1y2jVLyKuvvmr3ezVq1CjbvrCwMNq0aUOpUqU4cOAAs2bNYtq0aXzyyScZOOKMtXLlSsaNG8fUqVM5ePAgNWvWpG3btly5ciWjh5YpVK1a1e73aefOnbZ9Y8eOJSAggNWrV/Pjjz9y4cIFHn/88QwcbcYIDw+nZs2afPTRR/Huf/vtt5k7dy7z589n7969PPDAA7Rt25bbt2/b2vTp04cjR46wbds2Nm7cyI4dO3j66afT6yNkTobkOEuWLDE8PDzi3QcYa9euTfDYiRMnGlWrVrXb9sQTTxht27Z14ggzn4Su2ebNmw2z2WxcunTJtu1///uf4e7ubkRERBiGkXOvWWylSpUyZs+eneD+efPmGQULFrRdM8MwjBdeeMGoVKlSOowuc6pfv77xzDPP2N5HRUUZRYsWNWbMmJGBo8ocpk6datSsWTPefdevXzdy585trF692rbt6NGjBmAEBQWl0wgzn/v/bo+OjjZ8fX2NWbNm2bZdv37dcHV1Nb744gvDMAzj999/NwBj//79tjbffPONYTKZjPPnz6fb2DMbzThJHM888wyFChWifv36LF68GCNWqq+goCBat25t175t27YEBQWl9zAzhaCgIKpXr46Pj49tW9u2bQkLC+PIkSO2NrpmMHPmTB588EFq167NrFmz7G5nBgUF4e/vT548eWzb2rZty7Fjx/jnn38yYrgZ6s6dOxw4cMDu98ZsNtO6desc93uTkOPHj1O0aFHKli1Lnz59OHv2LAAHDhzg7t27dteucuXKlCxZUtcullOnTnHp0iW76+Th4UGDBg1s1ykoKAhPT08efvhhW5vWrVtjNpvZu3dvuo85s1CRX7Hz6quv0rJlS/Lnz8+3337LyJEjuXnzJqNHjwbg0qVLdkECgI+PD2FhYdy6dYt8+fJlxLAzTELXI2ZfYm1y0jUbPXo0derUwcvLi927dzNp0iQuXrzIe++9B1ivUZkyZeyOiX0dCxYsmO5jzkhXr14lKioq3t+bP/74I4NGlXk0aNCApUuXUqlSJS5evMj06dNp2rQpv/32G5cuXSJPnjxx1iT6+PjY/p+U//5+iu93LPbfXYULF7bbnytXLry8vHL0tVTglMW9+OKLvPXWW4m2OXr0qN3CycRMmTLF9ufatWsTHh7OrFmzbIFTduDsa5ZTJec6jhs3zratRo0a5MmTh2HDhjFjxgyVeZBke+yxx2x/rlGjBg0aNKBUqVKsWrUqR/xDRDKWAqcsbvz48QwYMCDRNmXLlk3x+Rs0aMBrr71GREQErq6u+Pr6xnk65fLly7i7u2eZv7Ccec18fX3jPOkUc318fX1t/83q1yw+qbmODRo0IDIyktOnT1OpUqUErxH8dx1zkkKFCuHi4hLvNcmJ1yMpnp6eVKxYkRMnTvDII49w584drl+/bjfrpGtnL+ZaXL58mSJFiti2X758mVq1atna3P8wQmRkJKGhoTn6WipwyuK8vb3x9vZOs/MHBwdTsGBB26yAn58fmzdvtmuzbds2/Pz80mwMzubMa+bn58cbb7zBlStXbFPa27Ztw93dnYceesjWJqtfs/ik5joGBwdjNptt18zPz4+XX36Zu3fvkjt3bsB6jSpVqpTjbtMB5MmTh7p167J9+3bbU63R0dFs376dZ599NmMHlwndvHmTkydP0rdvX+rWrUvu3LnZvn073bp1A+DYsWOcPXs2y/8/50xlypTB19eX7du32wKlsLAw9u7da3uK2M/Pj+vXr3PgwAHq1q0LwPfff090dDQNGjTIqKFnvIxenS7p58yZM8ahQ4eM6dOnG25ubsahQ4eMQ4cOGTdu3DAMwzA2bNhgLFiwwPj111+N48ePG/PmzTPy589vvPLKK7Zz/PXXX0b+/PmN559/3jh69Kjx0UcfGS4uLsaWLVsy6mOlqaSuWWRkpFGtWjWjTZs2RnBwsLFlyxbD29vbmDRpku0cOe2a3W/37t3G7NmzjeDgYOPkyZPG559/bnh7exv9+vWztbl+/brh4+Nj9O3b1/jtt9+ML7/80sifP7/x8ccfZ+DIM9aXX35puLq6GkuXLjV+//134+mnnzY8PT3tnuDMqcaPH2/88MMPxqlTp4xdu3YZrVu3NgoVKmRcuXLFMAzDGD58uFGyZEnj+++/N37++WfDz8/P8PPzy+BRp78bN27Y/s4CjPfee884dOiQcebMGcMwDGPmzJmGp6ensX79euOXX34xOnfubJQpU8a4deuW7RyPPvqoUbt2bWPv3r3Gzp07jQoVKhi9e/fOqI+UKShwykH69+9vAHFegYGBhmFYHzOtVauW4ebmZjzwwANGzZo1jfnz5xtRUVF25wkMDDRq1apl5MmTxyhbtqyxZMmS9P8w6SSpa2YYhnH69GnjscceM/Lly2cUKlTIGD9+vHH37l278+Ska3a/AwcOGA0aNDA8PDyMvHnzGlWqVDHefPNN4/bt23btDh8+bDRp0sRwdXU1ihUrZsycOTODRpx5fPDBB0bJkiWNPHnyGPXr1zf27NmT0UPKFJ544gmjSJEiRp48eYxixYoZTzzxhHHixAnb/lu3bhkjR440ChYsaOTPn9/o2rWrcfHixQwcccYIDAyM9++v/v37G4ZhTUkwZcoUw8fHx3B1dTVatWplHDt2zO4c165dM3r37m24ubkZ7u7uxsCBA23/cMypTIYR61lzEREREUmQ8jiJiIiIOEiBk4iIiIiDFDiJiIiIOEiBk4iIiIiDFDiJiIiIOEiBk4iIiIiDFDiJiIiIOEiBk4iIiIiDFDiJiIiIOEiBk4iIiIiDcmX0AERERLKK6Ohovv76a86fP0+HDh0oV65cRg9J0plq1YmIiDioS5curF+/HoAHHniAwMBA6tWrl8GjkvSkW3UiIiIO2LdvHwEBAQQEBBAaGkqzZs145ZVXMnpYks4UOImIiDjg8uXLlCxZkg4dOlCwYEEGDhzIyZMnM3pYks4UOImko7t37zJt2jQqVKiAq6srJpOJdevWZfSwJBMzDIO6devSpk0bu+0//PADJpOJadOmZczA7jl9+jQmk4kBAwZk6DgckdqxNm3aFMMw2LhxI//88w9Lliyhbt26dm2OHTtGrly5mDdvnhNGLJmRAicR/vsLNfYrd+7cFCtWjJ49e/Lzzz87pZ93332X6dOnU7RoUSZMmMDUqVOpXLmyU86d3cX3M7r/df369YweptN9+umnHDx4kFdffTWjh5IiP//8MyaTiQ8//DCjh5KkpMbq6enJM888Q8eOHfHy8uLkyZO88847dm0qVapE7969mT59Ojdu3EiPYUs601N1IrGUK1eOp556CoDw8HAOHDjA6tWrWbduHd999x3+/v6pOv/GjRtxc3Nj27Zt5MmTxxlDznFi/4zulzdv3nQeTdqKjo5m2rRpNG3alIYNG2b0cFIkZiF1586dM3gkSUtqrDdu3ODdd9/FZDJhGAa1a9emWLFicdpNnDiRzz//nLlz5/Lyyy+n6Zgl/SlwEomlfPnycW59zJw5k0mTJjFlyhR+/PHHVJ3/woULPPjggwqaUiG+n1F29c0333D69Oks/eW7fv166tSpQ4kSJTJ6KElKaqxvvvkmly9fZuzYscydO5fg4OB421WvXp0aNWqwYMECJk2ahNmsmzvZiX6aIkkYPHgwAAcOHIh3/44dO+jYsSOFChXC1dWVChUqMHnyZP79919bm2nTpmEymTh16hRnzpyx3VoqXbp0ss8F9utbdu/eTZs2bfD09MRkMqX6fD///DOPPPIIBQoUwMPDg65du3L69OkEP3uXLl3w8fHB1dWVEiVK8Pjjj7Nz584UXSdnW7JkCQ0aNMDNzQ03NzcaNGjA0qVL47RLzvVMz8+7ZMkSTCYT3bp1c/gYi8VCs2bNMJvNfPDBB8ke/507d/jggw9o27YtJUqUwNXVlcKFC/P4449z6NAhh8cBcOrUKX799Ve7GZz7r3WLFi0oUKAA3t7ejBw5klu3bgGwadMm/Pz8eOCBB/Dx8WHixIlERkbG24+jP+fkjjW206dPM3v2bAoXLsz06dMpX748x48ft433fj179uTMmTMEBgYmaxySBRgiYpw6dcoAjLZt28bZd+XKFQMwPDw84uybN2+eYTKZjIIFCxr9+vUzJkyYYDRv3twAjEaNGhkRERGGYRhGYGCgMXXqVMPDw8Pw8PAwpk6dakydOtWYPXt2ss8Vcz7AeOSRR4zcuXMbbdq0MZ5//nnjiSeeSNX52rVrZ+TLl89o166dMX78eKNly5YGYJQrV864deuW3Wd///33DZPJZOTPn9/o06ePMWnSJKNfv35G2bJljTFjxqToOqX0ZxSfUaNG0KLO/gAACoFJREFUGYBRrFgxY/To0cbo0aONYsWKGYAxevRou7aOXM/0/rzR0dGGl5eXUbly5Xj3x4x56tSptm0XLlwwatSoYeTJk8f48ssv7do7Ov6LFy8aZrPZaNasmfH0008bL7zwgtGjRw/D1dXVyJs3r7Fv3z6788b8XPr37x9njO+9954BGMHBwXHG/eijjxp58+Y1OnfubIwfP96oU6eOARh9+vQxvvzySyNv3rzGE088YYwdO9aoWLGiARjTp0+P00dyfs7JHWtsPXv2NABj/vz5hmEYRrdu3QzA2LNnT7ztt2/fbgDGpEmT4t0vWZcCJxEj8S/lN9980wCM9u3b220/cuSIkStXLqNmzZrG1atX7fbNmDHDAIx33nnHbnupUqWMUqVKxekjueeK+fIBjMWLFzv1fPd/4fbt29cAjC+++MK2LTg42DCbzUbRokWNU6dO2bWPjo42zp8/n6rrFJ+Yn1G5cuVsgWfsV1BQkK3tjz/+aABGlSpVjOvXr9u2h4aG2r6Ed+zYEe/nj+96ZsTnPXLkiC2QiM/9gdOxY8eM0qVLGwUKFDC2bduW4vHfvn3bCAkJidPfb7/9Zri5uRmtW7e2255YMNKsWTOjdOnS8Y4bMNatW2fbfufOHaNGjRqGyWQyChUqZBeghYWFGYULFza8vLyMO3fu2LYn9+ec3LHG2LVrlwEYDz30kBEZGWkYhmFMnTrVLpC6n8ViMQDD398/3v2SdSlwEjHi/1KeMGGC0aJFCwMwfHx8jN9//93umNGjR8f5izlGVFSU4e3tbdStW9due0KBU3LPFfPlU6dOnXg/T0rPF99f8jH7xo0bZ9s2YsSIBIOM1I4lITE/o4ResWfvBg0aZADGypUr45xn+fLlBmAMGjQozmdM6HpmxOfdunVrnOseW+zAad++fYa3t7fh7e1t/Pzzz6kaf2I6duxo5MmTxy54SSgYuXr1quHi4hJnNi5m3C1atIhz/ldffdUAjIEDB8bZF/Mz/euvv+Jsc/TnnNyxGoY1sKxfv74BGJs3b7ZtX7NmjQEYw4cPj3NMjLx58xply5ZNcL9kTVocLhLLyZMnmT59ut02X19ffvrpJ8qXL2+3fc+ePQBs3bqV7du3xzlX7ty5+eOPPxzqN6XnSqjUQ0rPd39OGoDixYsD2D3qv2/fPoA4uYWcOZaEtG3bli1btiTaJmYtTvPmzePsa9GiBUC8C3sTup4Z8XmvXbsGWB+BT8xPP/3Eu+++i7e3N1u3bqVChQpx2iRn/GC9Nm+//TY7d+7k0qVL3L17127/1atXKVKkSKLn2LRpE1FRUQmuGapVq1acbTHnTGzfhQsXKFOmDJDyn3NyxrpixQr27dvHI488wmOPPWbbXq1atSTP7+XlxdWrV5PsX7IWBU4iscT+Uv77779ZtmwZL7zwAp06dWLfvn24ubnZ2oaGhgLwxhtvpLrflJ7Lx8fHqedzd3ePsy1XLutfE1FRUbZtFosFk8mU5JdnasaSGmFhYZjNZry9vePs8/HxwWQyERYWFu+++GTE582XLx8At2/fTrTdoUOHuHnzJm3atKFs2bLxtknO+Hfv3k3Lli0Ba6BVoUIF3NzcbMlaDx8+TERERJLnWbduHV5eXjRt2jTe/Yn9riW2L3YQl9Kfs6NjvXXrlu2puPvzNZUvX568efPy66+/Eh0dHe+Tc7du3SJ//vxJ9i9Zi56qE0mAt7c3EyZM4KWXXuLo0aNMnjzZbn/MX+5hYWEY1tve8b4ckdJz3f/UV1qMLT6enp4YhsHFixfT7LOlhru7O9HR0fz9999x9l25cgXDMOL9ck7oembE540JBmICsYQ8++yzDB48mK+//ponn3wy3ifPkjP+N954g4iICL777js2bNhgS9o6bdo0fH19kzwerMHet99+S/v27W0BT1pI6c85tsTG+s4773Du3Dmio6OpWbOmXbLVXLlycfv2bcLDwzl+/Hic80ZHR2OxWOIN6iRrU+AkkoSXXnqJokWLMm/ePLvH8hs0aAD8d2smNZx5rrQ43/3q168PwLfffpvhY4lP7dq1Aeuj7/eL2Rbf7aCEZMTnrVq1KmazmWPHjiXazmw2s2DBAoYOHcqqVavo06dPnOApOeM/efIkXl5eNGnSxG77v//+y8GDBx0a+3fffUd4eHiaJ710xs85obFevHiRt99+mwceeIDBgwfH+6patSoQ/+2648ePEx0dTfXq1ZP9uSRzU+AkkoR8+fLxwgsvcPfuXV577TXb9pEjR5IrVy5GjRrF2bNn4xx3/fp1h/PeOPNcaXG++w0fPhwXFxcmT57MmTNn7PYZhsGFCxfSbSzx6d+/PwDTp0+3u1VjsVhsa9hi2jgiIz6vp6cnNWrU4OeffyY6OjrRtiaTiY8//phhw4axatUqevfubRc8JWf8pUqV4p9//uHIkSO2bVFRUUyYMCHemZ34rF+/HldXV9q2betQ+5Ryxs85obG+/PLL3Lx5k8mTJ7Nw4cJ4XzE53uILnPbu3QtAs2bNUvz5JHNS4CTigKeffpqiRYvy6aef2qqhV6tWjXnz5nHixAkqVapEt27dmDhxIiNGjKBt27b4+vry8ccfO3R+Z54rLc53v+rVq/P+++9z8eJFqlatylNPPcXLL7/M4MGDqVixIm+//Xa6jSU+/v7+jBo1it9//51q1aoxduxYnnvuOapVq8Yff/zB6NGjk1U+J6M+b9euXblx44ZDs1cmk4n//e9/jBgxgjVr1tCrVy9b8JSc8Y8aNQrDMGjSpAnDhg1jzJgx1KlTh1WrVsW7CPt+0dHRBAQE0KpVK7s1gWkhtT/nhMZ66NAhli1bRsWKFRk3blyCxyc247Rt2zZy5cpFhw4dUv4BJXNKm4f1RLIWR5IrfvDBBwZg9O3b1277vn37jF69ehlFixY1cufObRQqVMioU6eO8eKLLxpHjx61a5tQOoLkniu+5Idpdb7Ect8EBgYaHTp0MLy8vIw8efIYxYsXN7p162bs2rUrxWNJSHITYBqGYSxevNioV6+ekT9/fiN//vxGvXr14n0k39HrmZ6f1zAM4/z580auXLmMESNGODzm6Oho45lnnjEA4/HHH7dLHeDo+NesWWPUqVPHyJ8/v1GoUCGjZ8+exsmTJ43+/fsbgF0uqPt/P2JyHn3yyScJXsOErvWSJUsMwFiyZEmcfTF5kwIDA+Psc/Tn7OhYY5KVfvPNN/F+hhjnz583AMPX19due3h4uOHm5mZ06dIl0eMlazIZhpNXZYqIiNP07duXTZs2cebMGQoUKJDRw0nSCy+8wKxZs7hw4YLDi8kzSlqNdeHChQwdOpQff/wx1YXBJfNR4CQikomdOXOGypUrM2XKFF566aWMHk6SKleuTMGCBQkKCsrooSQpLcYaGRlJxYoVqV69OuvXr3faeSXzUB4nEZFMrFSpUixbtozLly9n9FAckpxkphktLcZ69uxZ+vXrR9++fZ1+bskcNOMkIiIi4iA9VSciIiLiIAVOIiIiIg5S4CQiIiLiIAVOIiIiIg5S4CQiIiLiIAVOIiIiIg5S4CQiIiLiIAVOIiIiIg5S4CQiIiLioP8Di650bgs+27AAAAAASUVORK5CYII=\n"
},
"metadata": {}
}
]
},
{
"cell_type": "markdown",
"source": [
"### The Model Weights and Biases Dictionary\n",
"\n",
"This cell prints the size of the weights and biases used in the trained model for reference."
],
"metadata": {
"id": "WRIOr1b-nVnm"
}
},
{
"cell_type": "code",
"source": [
"print(\"Model's state_dict:\")\n",
"for param_tensor in model.state_dict():\n",
" print(param_tensor, \"\\t\", model.state_dict()[param_tensor].size())"
],
"metadata": {
"id": "RQ49pMPzQ4xA",
"colab": {
"base_uri": "https://localhost:8080/"
},
"outputId": "844a109c-e4ff-4ad9-a2c5-9313b349a833"
},
"execution_count": null,
"outputs": [
{
"output_type": "stream",
"name": "stdout",
"text": [
"Model's state_dict:\n",
"descriptor.local_embedding.0.weight \t torch.Size([9, 25, 1])\n",
"descriptor.local_embedding.0.bias \t torch.Size([9, 25])\n",
"descriptor.local_embedding.1.weight \t torch.Size([9, 50, 25])\n",
"descriptor.local_embedding.1.bias \t torch.Size([9, 50])\n",
"descriptor.local_embedding.2.weight \t torch.Size([9, 100, 50])\n",
"descriptor.local_embedding.2.bias \t torch.Size([9, 100])\n",
"fitting_net.fitting_net.0.weight \t torch.Size([3, 240, 400])\n",
"fitting_net.fitting_net.0.bias \t torch.Size([3, 240])\n",
"fitting_net.fitting_net.1.weight \t torch.Size([3, 240, 240])\n",
"fitting_net.fitting_net.1.bias \t torch.Size([3, 240])\n",
"fitting_net.fitting_net.2.weight \t torch.Size([3, 240, 240])\n",
"fitting_net.fitting_net.2.bias \t torch.Size([3, 240])\n",
"fitting_net.fitting_net.3.weight \t torch.Size([3, 1, 240])\n",
"fitting_net.fitting_net.3.bias \t torch.Size([3, 1])\n"
]
}
]
},
{
"cell_type": "markdown",
"source": [
"### Plotting Training and Validation Loss for $\\Delta$MLP\n",
"\n",
"The loss at each step of the training process is displayed below."
],
"metadata": {
"id": "tdwrR_mFna7D"
}
},
{
"cell_type": "code",
"source": [
"import pandas as pd\n",
"\n",
"data = pd.read_csv(f'logs_csv/lightning_logs/version_{csv_logger.version}/metrics.csv')\n",
"fig, ax = plt.subplots(figsize=(6,5))\n",
"x = data['epoch'][~data['epoch'].isnull()]\n",
"y = data['train_loss'][~data['train_loss'].isnull()]\n",
"print(len(y))\n",
"plt.semilogy(y, label='Training Loss',color='dodgerblue')\n",
"y = data['val_loss'][~data['val_loss'].isnull()]\n",
"print(len(y))\n",
"plt.semilogy(y, label='Validation Loss',color='k')\n",
"plt.xlabel('Steps',size=14)\n",
"plt.ylabel('Loss',size=14)\n",
"plt.legend()\n",
"plt.savefig('loss.png', dpi=300)"
],
"metadata": {
"id": "N1XKrNWF7yMn",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 504
},
"outputId": "cad03803-2f87-4ba5-e499-2f1e778a2e9c"
},
"execution_count": null,
"outputs": [
{
"output_type": "stream",
"name": "stdout",
"text": [
"945\n",
"300\n"
]
},
{
"output_type": "display_data",
"data": {
"text/plain": [
""
],
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAiAAAAHFCAYAAADL6EKwAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAB/mElEQVR4nO3dd3hTZcMG8DtJ9550QNmz7L2H7ClLQQQZsi2KioqoCKiMV/kQ1CKICoosUYYiQ/Yoo2WPliXQskrp3is53x+nSbObdCSF3r/r6pXkzCdh5O4zJYIgCCAiIiKyIKm1C0BEREQVDwMIERERWRwDCBEREVkcAwgRERFZHAMIERERWRwDCBEREVkcAwgRERFZHAMIERERWZyNtQtQ3igUCjx69Aiurq6QSCTWLg4REdEzQxAEpKWlITAwEFKp8ToOBhAtjx49QlBQkLWLQURE9My6f/8+qlSpYvQYBhAtrq6uAMQPz83NzcqlISIienakpqYiKChI9V1qDAOIFmWzi5ubGwMIERFRMZjShYGdUImIiMjiGECIiIjI4hhAiIiIyOLYB6RAaGgoQkNDIZfLrV0UIqISEwQB+fn5/D+NSp2trS1kMlmJryMRBEEohfI8N1JTU+Hu7o6UlBR2QiWiZ1Jubi4eP36MzMxMaxeFnkMSiQRVqlSBi4uLzj5zvkNZA0JE9BxRKBS4e/cuZDIZAgMDYWdnx0kVqdQIgoCnT5/iwYMHqFOnTolqQhhAiIieI7m5uVAoFAgKCoKTk5O1i0PPIV9fX9y7dw95eXklCiDshEpE9BwqahpsouIqrRo1/g0lIiIii2MAISKi51L16tWxfPlyk48/cuQIJBIJkpOTy6xMVIgBhIiIrEoikRj9mT9/frGuGxERgSlTpph8fIcOHfD48WO4u7sX636mYtARsRMqERFZ1ePHj1XPt2zZgk8//RQ3btxQbVMf7ikIAuRyOWxsiv768vX1NascdnZ28Pf3N+scKj7WgBARkVX5+/urftzd3SGRSFSvr1+/DldXV+zZswctW7aEvb09Tpw4gf/++w+DBw+Gn58fXFxc0Lp1axw4cEDjutpNMBKJBD/++COGDh0KJycn1KlTB3/99Zdqv3bNxLp16+Dh4YF9+/ahQYMGcHFxQd++fTUCU35+Pt566y14eHjA29sbs2fPxrhx4zBkyJBifx5JSUkYO3YsPD094eTkhH79+uHWrVuq/dHR0Rg0aBA8PT3h7OyMhg0bYvfu3apzR48eDV9fXzg6OqJOnTpYu3ZtsctSlhhALODbcKD3b8D6y9YuCRFVNIIAZOZZ56c0p7n88MMPsWTJEkRFRaFJkyZIT09H//79cfDgQVy4cAF9+/bFoEGDEBMTY/Q6CxYswIgRI3D58mX0798fo0ePRmJiosHjMzMzsXTpUqxfvx7Hjh1DTEwM3nvvPdX+//3vf9iwYQPWrl2LsLAwpKamYseOHSV6r+PHj8fZs2fx119/4dSpUxAEAf3790deXh4AICQkBDk5OTh27BiuXLmC//3vf6paorlz5yIyMhJ79uxBVFQUvv/+e/j4+JSoPGWFTTAW8CQDuJEAPM2wdkmIqKLJygcarLTOvaPeAJxsS+dan332GXr16qV67eXlhaZNm6pef/7559i+fTv++usvzJgxw+B1xo8fj1GjRgEAFi1ahG+++Qbh4eHo27ev3uPz8vKwatUq1KpVCwAwY8YMfPbZZ6r93377LebMmYOhQ4cCAL777jtVbURx3Lp1C3/99RfCwsLQoUMHAMCGDRsQFBSEHTt24OWXX0ZMTAyGDx+Oxo0bAwBq1qypOj8mJgbNmzdHq1atAIi1QOUVa0AsQFYwZFrOSe+JiIpF+YWqlJ6ejvfeew8NGjSAh4cHXFxcEBUVVWQNSJMmTVTPnZ2d4ebmhri4OIPHOzk5qcIHAAQEBKiOT0lJwZMnT9CmTRvVfplMhpYtW5r13tRFRUXBxsYGbdu2VW3z9vZGvXr1EBUVBQB466238MUXX6Bjx46YN28eLl8urF6fPn06Nm/ejGbNmuGDDz7AyZMni12WssYaEAtQBhAFAwgRWZijjVgTYa17lxZnZ2eN1++99x7279+PpUuXonbt2nB0dMRLL72E3Nxco9extdWskpFIJFAoFGYdb+0l1CZNmoQ+ffrgn3/+wb///ovFixfj//7v//Dmm2+iX79+iI6Oxu7du7F//3706NEDISEhWLp0qVXLrA9rQCxAwgBCRFYikYjNINb4KcslaMLCwjB+/HgMHToUjRs3hr+/P+7du1d2N9TD3d0dfn5+iIiIUG2Ty+U4f/58sa/ZoEED5Ofn48yZM6ptCQkJuHHjBoKDg1XbgoKCMG3aNGzbtg2zZs3CmjVrVPt8fX0xbtw4/Pbbb1i+fDl++OGHYpenLLEGxAJkBTGPTTBERKWjTp062LZtGwYNGgSJRIK5c+carckoK2+++SYWL16M2rVro379+vj222+RlJRk0nTlV65cgaurq+q1RCJB06ZNMXjwYEyePBmrV6+Gq6srPvzwQ1SuXBmDBw8GALz99tvo168f6tati6SkJBw+fBgNGjQAAHz66ado2bIlGjZsiJycHOzatUu1r7xhALEAVROM5f9tEBE9l5YtW4bXX38dHTp0gI+PD2bPno3U1FSLl2P27NmIjY3F2LFjIZPJMGXKFPTp08ekRdq6dOmi8VomkyE/Px9r167FzJkzMXDgQOTm5qJLly7YvXu3qjlILpcjJCQEDx48gJubG/r27Yuvv/4agDiXyZw5c3Dv3j04Ojqic+fO2Lx5c+m/8VIgEazdmFXOpKamwt3dHSkpKXBzcyuVa351EvguAhjfFFjQrVQuSUSkV3Z2Nu7evYsaNWrAwcHB2sWpcBQKBRo0aIARI0bg888/t3ZxyoSxv2PmfIeyBqRAaGgoQkNDIZfLS/3aHAVDRPR8io6Oxr///ouuXbsiJycH3333He7evYtXX33V2kUr99gJtUBISAgiIyM1OhOVFmUfEDbBEBE9X6RSKdatW4fWrVujY8eOuHLlCg4cOFBu+12UJ6wBsQApa0CIiJ5LQUFBCAsLs3YxnkmsAbEAzgNCRESkiQHEAqQMIERERBoYQCxAynlAiIiINDCAWIBqFAw7oRIREQFgALEINsEQERFpYgCxAM4DQkREpIkBxAJU84AwgBARlZlu3brh7bffVr2uXr06li9fbvQciUSCHTt2lPjepXWdioQBxAKk7ANCRGTQoEGD0LdvX737jh8/DolEgsuXL5t93YiICEyZMqWkxdMwf/58NGvWTGf748eP0a9fv1K9l7Z169bBw8OjTO9hSQwgFsB5QIiIDJs4cSL279+PBw8e6Oxbu3YtWrVqhSZNmph9XV9fXzg5OZVGEYvk7+8Pe3t7i9zrecEAYgGcCZWIyLCBAwfC19cX69at09ienp6OrVu3YuLEiUhISMCoUaNQuXJlODk5oXHjxti0aZPR62o3wdy6dQtdunSBg4MDgoODsX//fp1zZs+ejbp168LJyQk1a9bE3LlzkZeXB0CsgViwYAEuXboEiUQCiUSiKrN2E8yVK1fQvXt3ODo6wtvbG1OmTEF6erpq//jx4zFkyBAsXboUAQEB8Pb2RkhIiOpexRETE4PBgwfDxcUFbm5uGDFiBJ48eaLaf+nSJbzwwgtwdXWFm5sbWrZsibNnzwIQ17QZNGgQPD094ezsjIYNG2L37t3FLospOBW7BUjZB4SIrEQQBGRmZlrl3k5OTpBIJEUeZ2Njg7Fjx2LdunX4+OOPVeds3boVcrkco0aNQnp6Olq2bInZs2fDzc0N//zzD1577TXUqlULbdq0KfIeCoUCw4YNg5+fH86cOYOUlBSN/iJKrq6uWLduHQIDA3HlyhVMnjwZrq6u+OCDDzBy5EhcvXoVe/fuxYEDBwAA7u7uOtfIyMhAnz590L59e0RERCAuLg6TJk3CjBkzNELW4cOHERAQgMOHD+P27dsYOXIkmjVrhsmTJxf5fvS9P2X4OHr0KPLz8xESEoKRI0fiyJEjAIDRo0ejefPm+P777yGTyXDx4kXY2toCENdDy83NxbFjx+Ds7IzIyEi4uLiYXQ6zCKQhJSVFACCkpKSU2jV3XBeEqssFYdiWUrskEZFeWVlZQmRkpJCVlSUIgiCkp6cLAKzyk56ebnK5o6KiBADC4cOHVds6d+4sjBkzxuA5AwYMEGbNmqV63bVrV2HmzJmq19WqVRO+/vprQRAEYd++fYKNjY3w8OFD1f49e/YIAITt27cbvMdXX30ltGzZUvV63rx5QtOmTXWOU7/ODz/8IHh6emq8/3/++UeQSqVCbGysIAiCMG7cOKFatWpCfn6+6piXX35ZGDlypMGyrF27VnB3d9e7799//xVkMpkQExOj2nbt2jUBgBAeHi4IgiC4uroK69at03t+48aNhfnz5xu8tzrtv2PqzPkOZROMBSj7gJx9DKTkWLcsRETlUf369dGhQwf8/PPPAIDbt2/j+PHjmDhxIgBALpfj888/R+PGjeHl5QUXFxfs27cPMTExJl0/KioKQUFBCAwMVG1r3769znFbtmxBx44d4e/vDxcXF3zyyScm30P9Xk2bNoWzs7NqW8eOHaFQKHDjxg3VtoYNG0Imk6leBwQEIC4uzqx7qd8zKCgIQUFBqm3BwcHw8PBAVFQUAODdd9/FpEmT0LNnTyxZsgT//fef6ti33noLX3zxBTp27Ih58+YVq9OvuRhALECqVgN55J7VikFEFZCTkxPS09Ot8mNuB9CJEyfizz//RFpaGtauXYtatWqha9euAICvvvoKK1aswOzZs3H48GFcvHgRffr0QW5ubql9VqdOncLo0aPRv39/7Nq1CxcuXMDHH39cqvdQp2z+UJJIJFAoym645Pz583Ht2jUMGDAAhw4dQnBwMLZv3w4AmDRpEu7cuYPXXnsNV65cQatWrfDtt9+WWVkA9gGxCJlazLNh5CMiC5JIJBq/iZdnI0aMwMyZM7Fx40b8+uuvmD59uqo/SFhYGAYPHowxY8YAEPs83Lx5E8HBwSZdu0GDBrh//z4eP36MgIAAAMDp06c1jjl58iSqVauGjz/+WLUtOjpa4xg7OzvI5fIi77Vu3TpkZGSoPvuwsDBIpVLUq1fPpPKaS/n+7t+/r6oFiYyMRHJyssZnVLduXdStWxfvvPMORo0ahbVr12Lo0KEAgKCgIEybNg3Tpk3DnDlzsGbNGrz55ptlUl6ANSAWod75VFZ0fywiogrJxcUFI0eOxJw5c/D48WOMHz9eta9OnTrYv38/Tp48iaioKEydOlVjhEdRevbsibp162LcuHG4dOkSjh8/rhE0lPeIiYnB5s2b8d9//+Gbb75R1RAoVa9eHXfv3sXFixcRHx+PnBzddvXRo0fDwcEB48aNw9WrV3H48GG8+eabeO211+Dn52feh6JFLpfj4sWLGj9RUVHo2bMnGjdujNGjR+P8+fMIDw/H2LFj0bVrV7Rq1QpZWVmYMWMGjhw5gujoaISFhSEiIgINGjQAALz99tvYt28f7t69i/Pnz+Pw4cOqfWWFAcQCsvMLn7MGhIjIsIkTJyIpKQl9+vTR6K/xySefoEWLFujTpw+6desGf39/DBkyxOTrSqVSbN++HVlZWWjTpg0mTZqEhQsXahzz4osv4p133sGMGTPQrFkznDx5EnPnztU4Zvjw4ejbty9eeOEF+Pr66h0K7OTkhH379iExMRGtW7fGSy+9hB49euC7774z78PQIz09Hc2bN9f4GTRoECQSCXbu3AlPT0906dIFPXv2RM2aNbFlyxYAgEwmQ0JCAsaOHYu6detixIgR6NevHxYsWABADDYhISFo0KAB+vbti7p162LlypUlLq8xEkEQODhUTWpqKtzd3ZGSkgI3N7dSueamq8CHB8XnawYCvWuVymWJiHRkZ2fj7t27qFGjBhwcHKxdHHoOGfs7Zs53KH8ftwD1GpBc402HREREFQIDSIHQ0FAEBwejdevWpX7tHLXQwQBCRETEAKISEhKCyMhIRERElPq1a3kWPs9hACEiImIAsYSeNQqfM4AQERExgFiERAIMKRj6zSYYIiIiBhCLsS+Y8i033/hxRESlgQMcqayU1t8tBhALsSuY7p81IERUlpTTe1trBVx6/imnpldfx6Y4OBW7hTCAEJElyGQyeHh4qBY1c3JyUk1nTlRSCoUCT58+hZOTE2xsShYhGEAsxJ4BhIgsxN/fHwCKvbIqkTFSqRRVq1YtcbBlALGQw+sW4OGfa3FsxJtA11nWLg4RPcckEgkCAgJQqVIl5OXlWbs49Jyxs7ODVFryHhwMIBaSl5kKeVI0UpP4GwkRWYZMJitxOz1RWWEnVAtxcnYBAGRnpFm5JERERNbHAGIhzsoAkplu5ZIQERFZHwOIhTi7ugIAcrIYQIiIiBhALMTFRawByc1kEwwREREDiIW4KgMIa0CIiIgYQCzFraAJJi+bAYSIiIgBxEJcXcUakLwsNsEQERExgFiIe0EAkbMGhIiIiAHEUjzcxSaY/GzWgBARETGAWIi3u1gDIuTnqlYSJCIiqqgYQCzEx9NF9TwjI8OKJSEiIrI+BhAL8XCyA2R2AIDkFDbDEBFRxcYAYiHOdoDUXqwFSUhhR1QiIqrYGEAsxF4GSOzFjqhPkxlAiIioYmMAsRCJBLBxEGtAEpPZBENERBUbA4gFKQNIAmtAiIiogmMAsSAHZ7EJ5nECa0CIiKhiYwCxIOWKuA8TWANCREQVGwNIgdDQUAQHB6N169Zldg8PNzGAPE5kACEiooqNAaRASEgIIiMjERERUWb38PcSm2AexbMJhoiIKjYGEAsK9BZrQJ4kpUMQrFwYIiIiK2IAsaAgHzGA5GSm436qlQtDRERkRQwgFqRcEVeRk4YnXA6GiIgqMAYQC1KOghFy0pGvsHJhiIiIrIgBxIJcXQtrQPLkVi4MERGRFTGAWJB6DcjC41YuDBERkRUxgFiQMoAoctJxPcHKhSEiIrIiBhALcnNzAwAospOtWxAiIiIrYwCxoEqVKgEAFOlPISgUyMm3coGIiIishAHEgpQBBAo5FJmJSM+1bnmIiIishQHEguzs7CB18gQAyNOeMIAQEVGFxQBiYVIXPwCAIu0J0vOsXBgiIiIrYQCxMJmrGEBYA0JERBUZA4iFaQSQHCsXhoiIyEoYQCxM6lrYBJPGGhAiIqqgGEAsTFUDkh7HJhgiIqqwGEAszMNbrQmGnVCJiKiCYgCxsPd7FUxGxk6oRERUgTGAWFiruhwFQ0RExABiYX5+hQEkJ0+wcmmIiIisgwHEwpQBBPJcpKWlWLcwREREVsIAYmGOjo5wcHYFAKQmPLFyaYiIiKyDAcQKPHwCAADJcQ+sXBIiIiLrYACxgqA6jQEAT26dt3JJiIiIrIMBxArqNGoFAHhy66yVS0JERGQdDCBWUK9JawBA/K0IK5eEiIjIOhhArKBek5YAgIy4u0hISLByaYiIiCyPAcQKvDw9YONbBwBw9iybYYiIqOJhALECWylgFyT2A4mIiIDA+ciIiKiCYQCxAhspYBfYFACw6cgNtP4ReJxm5UIRERFZEAOIFdjJAJlHZQDAf/cf42kmsP6ylQtFRERkQQwgVmAjBWRugQAAecojAICrvTVLREREZFkMIFaQmQfI3DUDiLejNUtERERkWQwgVuBuD8jcxOnYhewUKHIy4GRr5UIRERFZEAOIFTT2AyQObpDYOQEA5KmPIedIGCIiqkAYQKxkSH1JYT+Q1MdQMIAQEVEFwgBiJQ42hc0w8pRHDCBERFShMIBYib1MrSNq6iOsOgfEpFi5UERERBbCAFIgNDQUwcHBaN26tUXuJ9aAFI6EuZkADNxkkVsTERFZHQNIgZCQEERGRiIiwjIr1DrYADL3giaY1McAgJQci9yaiIjI6hhArMReplYDkvrIyqUhIiKyLAYQKxFrQDQnIyMiIqooGECsxF6jD8hDK5eGiIjIshhArMTBBpB5VAEACDnpUGQmW7dAREREFsQAYiX2MkBq7wypszcAID85xsolIiIishwGECtxsBEfZZ7VAAD5idFWLA0REZFlMYBYiX1BALHxrAoAkCexBoSIiCoOBhArcVAFkIIakCTWgBARUcXBAGIlDjLxUcYaECIiqoAYQKxEufacjRf7gBARUcXDAGIllV3FR1UNCEfBEBFRBcIAYiW+zsC+0UDflmINiDz1MYT8XCiEIk4kIiJ6DjCAWFF9H6B2FV9IbB0AQYA8+QFy5dYuFRERUdljALEyG6kEMg+xGSY/KRo5DCBERFQBMIBYmVQK2PjWAQDkxV5Dbr6VC0RERGQBDCBWJpMAdkEtAQC5MWfZBENERBUCA4iViQGkFQAg9z4DCBERVQwMIFYmkQD2BQEk70kUklLSrVwiIiKisscAYmUyCSBzD4DMvTIgKHDl8kVrF4mIiKjMMYBYmazgT0DZDHPpwlkrloaIiMgyGECsTCoRH+2qigHk2iUGECIiev4xgFiZY8GquMoakCgGECIiqgAYQKzMxU58VA7FvX/nBlJTU61YIiIiorLHAGJlTrbio8zFFzJPcV2Y8+fPW7FEREREZY8BxMqUNSBAYT+Qs2fZDENERM83BhArq+pe+FzZD+TISQYQIiJ6vjGAWFlVd2DVAGD9kMIJyfYdP4uDd61bLiIiorLEAFIO9KsNdKlW2BE1P/4/rAlLsnKpiIiIyg4DSDkypo0nbHxqAQBib7IZhoiInl8MIOXIvK5As+ZiLUjS3YvWLQwREVEZYgApRxxsgIaNmwAAbkddwkNOB0JERM8pBpBypk6DpgCAvEeX0WEtsOSElQtERERUBhhAypk6wWINSN6TKAj5Ofj+nJULREREVAYYQMqZgMpBkDh6AIp85D25bu3iEBERlQkGkHLGzkYCu0CxFiT34SUrl4aIiKhsMICUMzIJYFsQQLIub0NebJSVS0RERFT6GEDKGVspYFe5OQAg6+pOxC5rhbS0NCuXioiIqHQxgJQzMing1HwEXDpMg8TWEUJuJm7e+s/axSIiIipVDCDljK0UkNq7wGvE97D1bwgAuH03xsqlIiIiKl0MIOWMTO1PROZZFQDw3z0GECIier4wgJQztmp/IjYeQQCA6GgGECIier4wgJQz+mpA7j+4b6XSEBERlQ0GkHJGowakIIA8vB+D/zsFTN0FyBVWKhgREVEpYgApZ9RrQNx8xSaYRw+isfDrVfjr6AUcibZSwYiIiEqRjbULQJps1AKIh59YAxIf+xDYOh0SW0fcfiUT1dyB2l6a5ykEYOQfQCVnILS/BQtMRERUDKwBKWekksLnHj5+gMxW9VrIy8KiE0CP9UB0suZ5kU+B8EfArluWKScREVFJMICUM+p9QHycpZDau2rsV+RmAgDOxWqeJ6g/F0BERFSusQmmnHG0BeZ3BfIUwOM0QJGZqLFfnvIQUt86cJAZvoZCENeUISIiKq9YA1IOTWgGTGkBNPUDnJqP1NgnT34AAHDQio7qeUPBGhAiIirnGEDKsQBXwHP4t/Aesx72tboCKAwgdkZqQOQMIEREVM4xgJRjng6AzMUXzq3GwMarOgAgvyCAaPfzkKhVgbAGhIiIyjsGkHLM06HwucyjCgBAniIGkDwjE5IxgBARUXnHAFKOeegLIAU1INrNLOp9QNgEQ0RE5R0DSDlmKwP61xaf2xQEkNyHF/HoizpYMfcNg+dxGC4REZV3DCDl3PcDxEeZe0ENSFIM8uNv49DO3yCoJQ2NGhCuF0NEROUcA8gzQtkEo5SVkYb/O5So91j2ASEiovKOAeQZ0CkIkDp7Azb2GtuX7r6jeq5e6cEAQkRE5R0DyDPg+wFAl2oSuLQeB9vKzWDj1wAAkJ9wVxU21EMHAwgREZV3DCDPADd7sTOq18jVCHj/AuyCWgIA8hPuIC1HPEa94ylHwRARUXlXogBy//59HDp0CJmZmaptCoUC//vf/9CxY0f07NkT//zzT4kLSYBM7U/KxrsmAECecBeJWeI21oAQEdGzpEQBZO7cuXj55Zdha1u4ZPzChQsxZ84cnDp1CocOHcKQIUMQERFR4oKaa+jQofD09MRLL71k8XuXBfVVcm28agAQa0ASs8VtDCBERPQsKVEACQsLQ8+ePVUBRBAEfPfdd6hfvz5iYmIQHh4OZ2dnfPXVV6VSWHPMnDkTv/76q8XvW1Y0akB8xBqQ/MS7SGYNCBERPYNKFEDi4uJQrVo11euLFy/i6dOnePPNN1GlShW0atXKajUg3bp1g6urq8XvW1Zs9DTB5CdGIz5DDoB9QIiI6NlSogCiUCigUBQOAD1y5AgkEgm6d++u2la5cmXExsaadd1jx45h0KBBCAwMhEQiwY4dO3SOCQ0NRfXq1eHg4IC2bdsiPDy82O/jWSBTm2lM5hYIyOwART5u3LoNQHMYrr6ZUPfeBrquA648KdNiEhERmaREAaRq1aoaX/w7duxAQEAA6tWrp9oWGxsLDw8Ps66bkZGBpk2bIjQ0VO/+LVu24N1338W8efNw/vx5NG3aFH369EFcXFyx3sezQL1WQyKVwi6wCQBgwYRuOHb6gkazi1wB5Mk1z5/6D3AvBZi2u+zLSkREVJQSBZDhw4cjLCwML730EsaMGYMTJ05g+PDhGsdERkaiZs2aZl23X79++OKLLzB06FC9+5ctW4bJkydjwoQJCA4OxqpVq+Dk5ISff/7Z7PeQk5OD1NRUjZ/ySDncVsnr1bWw8WsARWospr8zRyOAXIkDGq8CVpzRvU5mXtmWk4iIyBQlCiDvvfceWrdujW3btmHjxo1o3Lgx5s+fr9ofHR2N8PBwdOvWrYTFLJSbm4tz586hZ8+eqm1SqRQ9e/bEqVOnzL7e4sWL4e7urvoJCgoqtbKWphStAGIX0Ai+k/8GAESF78fT2EeqfV+eBLLygWWnda+TmAXM2APcSy7DwhIRERXBpiQnu7m54fTp07h69SoAoEGDBpDJZBrHbNu2Da1atSrJbTTEx8dDLpfDz89PY7ufnx+uX7+uet2zZ09cunQJGRkZqFKlCrZu3Yr27dvrXG/OnDl49913Va9TU1PLZQhp6qe7zdanFuxrdETO3TBMXfQbbFtNQMreBUhJiEIO7OE9+hcAvjrn/X0TuJEA7B9T9uUmIiLSp0QBRKlRo0Z6t1erVk1jlIwlHThwwKTj7O3tYW9vX/SBVtauCvDLYMDVHhj2e+F25zbjkHM3DAnHvofN5b+Rc+eEal/WlZ3IlU+CnUz3eneTdLdtuQb4OgHda5TBGyAiIlJToiaYtLQ03LlzB3l5mh0LtmzZgtGjR2PSpEm4cOFCiQqozcfHBzKZDE+eaA7nePLkCfz9/Uv1XuVNt+pAC6236NRsBGRuAZAn3kPOnROQ2LvAo3Y7AIA87QmyDPT5sNH6k/8vCfjgADDhr9IvNxERkbYSBZAPPvgATZs21Qgg33//PV599VVs2rQJP//8Mzp16qTRNFJSdnZ2aNmyJQ4ePKjaplAocPDgQb1NLM8biQRY0qNwZlSpozv83joBm0r1AYkUXq/8BNe6XQEA8vQ4ZMv1X8dW608+sXA2fb3DeImIiEpTiQLI0aNH0bNnTzg5Oam2LVmyBJUrV8axY8fw+++/QxAEs2dCTU9Px8WLF3Hx4kUAwN27d3Hx4kXExMQAAN59912sWbMGv/zyC6KiojB9+nRkZGRgwoQJJXk7z4xRjYALUwpf2/jURMDsywicFw3n5iOgcKoEAFCkxSHXQACRaf3J26g10+QpQEREVKZK1Afk8ePH6Nu3r+p1VFQU7t+/jy+//BKdOnUCAPzxxx84duyYWdc9e/YsXnjhBdVrZSfRcePGYd26dRg5ciSePn2KTz/9FLGxsWjWrBn27t2r0zH1eeZqD4xvCqy7JL6WyGxh41EFAJDvJH4O8nTDASQpG5h/FJgvVpZoNMnk5ENvvxEiIqLSUqIAkpOTAzs7O9Xro0ePQiKRoHfv3qptNWvWxF9/mdexoFu3bhCKaAeYMWMGZsyYYV6BnzNuBvrOKpwLakDS45Cbb/j8tRcLA4hUbabV7Hwx4BAREZWVEjXBVKlSBZcvX1a93rVrF7y8vNCkSRPVtoSEBLi4uJTkNmSAo4H4KHMRA4g8LQ45BmpAtKlPZKZ+ztFo4ODdYhaQiIjIgBLVgPTr1w+hoaF477334ODggL1792Ls2LEax9y8eRNVq1YtUSFJP0db/duVAUSREY+sXDmAottT5Gr9PrILak1y8oGxO8TnV6YZrnEhIiIyV4lqQObMmYOqVati2bJlWLRoEfz8/PDZZ5+p9sfFxSEsLAxdunQpcUHLWmhoKIKDg9G6dWtrF8VkDgbio9TFR3wiKBCfkGjSteR6akDUO6Om5+qek5gF3Eww6fJEREQaSlQD4u/vj2vXrqmGxHbp0gVubm6q/fHx8fjqq6/Qp0+fkpXSAkJCQhASEoLU1FS4u7tbuzgmMRRAJDJbSJ28oMhMLFigT3c2VG1qixojR0+/EYWeLjnNfxAfD48FanoWXV4iIiKlEs+E6ujoiIEDB+rdFxwcjODg4JLeggzQnkxMndSlEhSZiVh/Kg4uVRoWea18tYChbIJRDx36AohSxCMGECIiMk+pTMUOAA8fPsTFixeRmpoKNzc3NGvWDJUrVy6ty5Me6iNXtMlcKyE/7jqu3o3DBybMSq/eB0TZBKM+EMnYoCROXEZEROYqcQC5ffs2pk+fjkOHDuns69GjB1auXInatWuX9Dakh5H8AWlBR9SEX19B+olQVHrjACQ2dgaPl+upAZGbWANCRERkrhIFkPv376NTp06Ii4tD/fr10aVLFwQEBCA2NhbHjh3DgQMH0LlzZ4SHh5fLFWafdUXVgCjl3DmOnLsn4VCnm8Hj5Xr6gKiHDrmxGpAiyklERKStRAFkwYIFiIuLw8qVKzF16lRIJJrfiKtXr8b06dPx2WefYc2aNSUqKOkKdDW8T+qs2fE0+8a/BgPIozRoNNMom2A0AginZyciolJUomG4+/btw6BBgzBt2jSd8AEAU6dOxaBBg7Bnz56S3IYMaGJk5nmJRPOPNuv6Pr3HKQRgxh7gqdpidPo6oeazmoOIiEpRiQJIXFwcGjVqZPSYRo0a4enTpyW5DRnxWTf9251ajoLU2QcuncXp6vMenIc8LU7nuNXngHOPNbeZWwPCTqhERGSuEgUQX19fREZGGj0mMjISvr5Fz0NBxTO2CbB9hO52W986qPxFHLyGfwvbwKYAgKyrO3WOWxKme+7C4+Kjer8PrpBLRESlqUQBpE+fPvjrr7/w008/6d3/888/4++//9ZYMZdKl0QCtAgAXPQMcFE2izm3GAUASP7nY8jT402+tsA+IEREVEZK1Al13rx5+PvvvzFlyhQsX74cXbt2hZ+fH548eYJjx47h2rVr8Pb2xrx580qrvGSAnZHlXly7vYPs878h+9FVJG2fCZ/XNhR5vd+vAZ8dK3ydb6wJxoxyEhERASUMIFWrVkVYWBimTp2KI0eO4Nq1axr7X3jhBaxateqZGIIbGhqK0NBQyOUmLh9bztgaqcuS2NhhaehPmDGsPTLPbURWi1FwbKh/9lql97UmLzMWQEpTcjbwIBVoVKnoY4mI6NlVoiYYAKhTpw4OHTqE6Oho7Ny5E+vXr8fOnTsRHR2NgwcPYtu2bejRo0dplLVMhYSEIDIyEhEREdYuSrFMaaH5+hW12ddXDwAGvdAGrt3eAQAk/j4NiqwUs65vtAakFKtAOq4FBmwSp3cnIqLnV6lNxR4UFKS3puP69es4cuRIad2GDHi9OdA6EKjlBSRkAjcSgM0FFVL2NmINiXu/z5B1ZSfy428j+a8P4DVytcnXt9REZMpVdw/fFd8PERE9n0pcA0Llg1QCNPUXO6NW8wCcbAv32cvEheukdk7weuVHAED6qR+QFaV/bhB98rRapkyt9fgvCWj/E7D+ssm3Eq9v3uFERPSMYQB5Tjmo1W3Z2wC2BZ1UHWp3hUvH6QCA+HUvI/fBBZOup10DojBxobpPDgGP0oFPDpt0G5OuSUREzz4GkOeUo54aECXPIctgX7sbhJw0xK3qi/zE6CKvp90HRCOAGDkvK9+08mpj/iAier4xgDynnLRqQNQDiMTWAb4Td8A2sCkU6XF4+vNQKHIzdS+ixlgAMaa484dw9V0ioucbA8hzSrsGRHuYrtTRHb6T/4LUxRd5Dy4gcctkCEbaPbQDiGDguc55xQwSzB9ERM83s0fB9O/f36zjr1y5Yu4tqBSo9wGRSQCZnqhp41kVPuO3Im5lD2Se2wi7ys3h1v09vdfT7oRa1jUg7ANCRPR8MzuA7N271+yb6Fspl8qWdidUg8fV7grPocuR9OebSP57Nmz9GsCx4QCd474JB+6nAh93Fl8X1Ql1xRlg2eliFh6sASEiet6ZHUDu3r1bFuWgUuZgAyx8AcjOB3yc9B/T3B+4EAu4dApB7sNLyDj9I+J/GQGXdpPh1usjyFwLpyN9mgn8cB4YXE+cpVS7BkQhiHN4uNkDj9JKFj4AGEwggiCuf0NERM82swNItWrVyqIcVAbGNNF8PaUFcO0p4G4PdKsOZOaJAUQikcDrpVDIk6KRfWM/0o6tQM7dMPi9fRISma3GNQZsAta+CLQM0Lz2uB3AsRjgxAQgJbvkZdeXP9ZdApafBjYNAxpwgWUiomcaO6FWIB93BjYOA74fAIxsqFmTILGxg++U3fCdvAtSJ0/k3j+L1P2L9V5n9kHdJphjMeLzbVGlM426vgAy7wiQlA3MOVTy6xMRkXUxgBQIDQ1FcHAwWrdube2iWIz2H75EZgPHhgPgOfw7AEDKvgXIvLxD57y4DOD848LX6mFh7UVg/tGSl81YJ1R2UCUievYxgBR41hejKw59I2MAwKnFKDi3nwwICiSsH6U3hEz8u/B5Vl7h86RSaH4BjI+yYf4gInr2MYBUYOp9Od9oBVRyLtgukcDrpZVwbDQYQl424n8eipS9CzTmCVEPAYkmho6kLM3XgmB4lV2GDCKi5xsDSAWm3gdkdkcgfGLha6nMBj4TtsKly1sAgJS985G4eRIEue7c6olZOpv0avaDOCpHacouoNPawhVw1bEJhojo+cYAUoHJtIazqgeSABdAIrOF17AV8BqxGpBIkXHmZ73TtpsaQACx/4jSv3eAx+nAntvFKDwRET3TGEAqsE5VxUdftXlCuhaMsp7ZtnCbS4cp8Hl9GyS2Dsi+tgtx33ZFflKMan+CGQFEH30BxmgNSMlupyEmRZw0LbmU+q4QEZFpzJ4HhJ4fga5A+CTAza5w288vAvGZurUjTo0HQzb9AJ7++CJy759F7NIW8Bm7GQ71eur07TBGOTW7eidTfedbqpVlyBYxQEU+BVYPtNBNiYiINSAVnZ+z5sJ1NlLA3wXwdNQ9tmuXjvCfdQ62VVpAkZGAuFV9kLx7LuLT9HTiMCBXrvkI6O/EaiyAlGY4UdbenHpQihclIqIiMYCQXjZafzNC+wEfdABsvKvD760TcG77OiAokPrvF7i7sDEyzm6AoJDrv5gaZfDIUTs0PlP3OFMXuyst7NhKRGRZDCBkkHozzMC6gHNBTYnUzhHeo36Cz/jfIXX2Qf7Tm0j4bQzifx4ORa7x9hhl8MhRGw1z8K7uSBhLBwLmDyIiy2IAIYNaBWq+drLVet3sZQTOvQP3AQsBG3tkXd2JuO97Ij/5ocFr5siBc4+Bf25pbr+XrPna0oHA0jUuREQVHQMIGfR1b3Hl26/7iK8d9XRZljq4wr3XR6g0bR8kDm7IvXsSsV81Q+alP/Ve804SMOx33ena5doTkrEGhIjoucYAQgZVdgP+GQUMqy++1q4BUedQu6vYQbVyMygy4hG/9iXE//IK5OnxGsd9clj/+XkKzWYXo51Q9ez84jjw4mZxorPV54CDd4xcwMRrEhFR2WEAIZM5GgkgAGDrWxv+75yGW6+PAakMmRe24PGSYIO1IerkgmboMDcPrDkPXHoirpi76ATw+t9FnqKB+YOIyLIYQMhkUonhfa4Fc4lIbOzhMeAL+L19GrYBjaBIf6pWG/LU4Pkj/gDOqHUdKe5EZHeSjOw0gjUgRESWxQBSIDQ0FMHBwWjdurW1i1KuLe2lf7tyITsl+6qt4D/rrEZtyKPPayFl3+dQ5KTrvcar2wqfF7dTaJ6Bxe2IiKh8YQApEBISgsjISERERFi7KOXay8HAj4N0tzvo6aCqURtSpQWEnDSk7PkUj76ojbTj30HIz9E4XmFiHxAIwPV4YO5hcW2ZPLU5RXKKnorE0CWJiMiCGEDIbD1rAIEumtvsjUzqb1+1FfzfjYD32M2w8a4JRdoTJP35Jh59UQfpp9ZAUOhWWxy+C6Tl6LlYgT4bgF8vAx8f0lxh92aCmW+mAJtgiIgsiwGEzCaRAK800txmJytshpnfFZjVXuscqRTOLUYiYE4UPF8Khcw9EPLk+0jcMgUpuz/RuUdqLjBjj/77q2eFyHjNAJJfzCYYzgNCRGRZDCBULMMaaL62lwEHxgC7XwUmNAPeaqP/PImNHVw7vYGAj2+LE5gBSD30JXIfXNQ59kg00Gkt8DjNcDkcbIBY/V1KzML8QURkWQwgVCxBbsCRsYWv7WSAuwPQ0NfwObW9Cp9L7Rzh3usjODYdDijkiP26DZ582xXpZ9ZBkVu4OMz9VOA7I91yHqYCAzfr36ddq7HpKtBjPRCTUvSxRERUthhAqNjUR76Y0ofCSU8/Ea9h38I2sCkgz0POf8eQuGkCHn4agMQ/QlS1Ir9d0QwN6vfKyodB2s0xHx4EbicCC47qP56IiCyHAYSKTX1iMrmeALL2RWBgncLXtjLdY2TuAfB//wIC596Bx8AlsPGpBSE7FeknViJ2aXPELmuD9FNr0HetkXYYAwzVauhbfVeflGzgh/Ol08RDRESaGECo2NQnJtNZywVA9xpAaP/C1zIDE5lJJBLYeNeAW8/ZCPjoJiq9cRBOzUcCMlvkxkQgccsUXP8wEAlbpiAn5izkJg5ZMdQh1dShuu8fABYeB0b+YdrxRERkOiODJ4lMp68GRJvMhLgrkUrhULc7HOp2hzz9KTIifkX6yR+Q//QmMk6tQcapNUgLagb7tlPg3Po1SO1dDF5LXygCgBwjzTbqDt8TH+/p6TNCREQlwxoQKpGq7uJjr5pFH2tr5t82mYsv3F6YhYCPrqPSm0fh1HI0YGOPzPsXkfTHG4hd2hJ58f8ZPN9QKCruZGVERFR6GECoRFb2A1b0AcY3LfpYcweatA4UHyUSCRxqdYHPa7+h8oJH8Bi6HDL3ysh/ehOxS1sgefdcnVV3Ac0mmFz12VJNrAEhIqKywwBCJdLYDxhSX5ycrCh5CmBRd+DddsDlqcB3/Ywf3zFId5vM2QtuXWfC/90I2FVrCyE7Fan/foFHn1VD0o5ZyE95pDpW2Qk1KQs4Gl14jcx8sXlmW5Tx+5vwlsymEIBzj4GsvDK4OBHRM4R9QMhi7GXA6MaFrwfVNTzbKaA5ykabzD0AfjNPIuvKDqTsX4i8B+eRdmQZ0o59A4f6feDcagxaZw+Aj6cr8hVAqtq07pl5QM1vS/5+iuOXS8D8o0C7ysCWl6xTBiKi8oABhMrc/3oAq86JU7Rrc7IVA4GbnTj9utKFKZq1FvpIpFI4NR0GxyZDkR21F6kHFiHnzglkR/6D7Mh/AIkET/wawC6oFeyCWsG2SnPInLyRfesQIJXBufkrkDp5lOp7Lcqmq+Lj6YcWvS0RUbnDAEJl7pVGumvHKG0aBnx5EvikM9BvY+F2L0egX23g7X1FX18ikcAxuB8cg/shLzYKGec3IvP8JuTH/4e82EjkxUYiI+JXnfOS/3of3q/+Aqemw4r5zkTX48WF81pXLvpYaVm06xARPYMYQMiqmvkDGw18/zvYiGvLHLwrrgez8WrR17P1bwCP/p/Do//nkKfGIvf+OeTeP4uc+2eR9+gKFOlPYFu5OYTsVOTFXkP8upfhNXINXNq9bnKZN1wBzjwU+4h82FFcmRcAwicBfs5GTzWprwwRUUXAAELlWkNf8efLk8aP83QAkrI1t8nc/OHYcAAcGw7QOV5QyJH4+1RknP4JiZsnIj/hDu6+9hnWXZZicgugipv++yRkAh8dKnyt3pQSm2ZCADG+m4iowuAomAKhoaEIDg5G69atrV2UCstY84Sbnf7tjjbA5uFinxFzSKQyeI1cA7deHwEAUvcvRJt+o7H2bDam/mP4vNgMrddq07Tb6JlqXhubYIiIRAwgBUJCQhAZGYmICCNLr1KZal/F8D5Xe91tb7cFroeI5xWnaUMikcBjwEJ4vfITILVBfPhmxH7dDufCT0MQ9F8zKcvw9WxMKAMDCBGRiAGEyo03WomPjnoaBt30BBDl8SXl0u51VJq2F1InT+Q9uoQny9sjsEk3pJz8CfL0p6rjbiUCo7cbvo4p09EzgBARidgHhMqNTlXFDqk+jrr7XLWaYAJcAPtS/NvrULcHAuZcR/LfHyLj7K+IvXoUuHoUkEhhX6MDBl7rgQt+Y2HjY3jOeUOL36ljJ1QiIhFrQKhc6RgE1PPR3e6iFUDsTehvYS6ZayV4v/ozAj+9B/f+X8AuqCUgKJBz5wT+WbMAsctaQ56RaPB8UwKIpf/BCQLw43ng5H0L35iIqAgMIPRM0K4BMeG7vthsPKrAvffH8J91FoGf3oPXiNWw8akFRWYi0o4sM3je6QfAK38CN3SXpVGxdBPM4XvA58eBUdsse18ioqIwgNAzwVkrgOhbS6V79dK/r41XNbh0mAKPF78CAKQdW4H08F+QH38HgqDZ6eN/J4FTD4DeG4DZB4DoZN3rWTqA3E+17P2IiEzFPiD0THDX6oSarWdF2+V9gH9uAXMO6e4rKcfGQ2BbpQXyHpxH4sbxAACpszfsglrDrlobONTuBvsaHSGxEZPS5mvAhVjg3zGa17F0HxB2eiWi8oo1IPRMcLUH5nQsfK2vD4i7A/BqY6CKa+G2l4NL5/4SiQSVpu6BW6+PYFe1DSCzgyIjAdnX9yJ132eIC+2OBx974+mPQ5AWtgr5SfdxIwF4mCo2g6iuUzrFMRkDCBGVV6wBoWfGtFbA4jDxuYORv7k/DgI+PQK81wFoEyjWRNw23HcUAPBdP3FSsS+OGz5G5loJHgMWAgMWQsjPQe6jy8iNDkdO9GlkX/8XivQ4ZF3diayrO5EEwL7OC2gaMQGOTYdj/wQn1PcxHgiy8oBZ+4E+tYDB9YyX11QMIERUXrEGhJ4pbQsWfHutieFjGvgCW18Wj5VIgC976j9OvRallicw1sg1tUls7GFftTVcO4fAZ8x6VP7sMfxnnYN7/y9gX6MjIJEg59ZhJGwYiyfLWuPavXi8tBU4YWQ0ys8XxSakt/bq35+VZ9pIG41ymnc4EZHFMIDQM2XNQODnQcCkFqaf0zIAsNXzN72ud+FzCcR5Rf5+BehZw/isrPpIpFLYBbWAe++P4TfzBALn3oV7v88gdfVDXmwkZo7ug6N7d0CRUziXe04+sOoccDMBSMkR+40Ykp4LNPsBGLzFvHKxBoSIyis2wdAzxd0B6GF4LjCDKjkDD9M0t9mohRLlF3UTP+CnF4Evw8QRLcVl41UN7n3mwqnpS3jyTSc8vHkeuDkUsLGHQ90ecGw4CItqDMK6u5Wx+ATQ3B+ISTF8vYhHYsfbq3HmlUPGXzGIqJzif09UIXSrprtNvVZEe3SKo23p3NfWvwH83j4F1y4zIfOuAeTnIDtyN5K2Tsdng6sgdllbpB39BmdvaSaLXDkw7R/g10viZGLqNRknYsRtplB/X/KynDyFiMhMrAGhCuHjzmItyPbrwL2CmgZ9NSBK2jOvloRtpbrwHLYcHkO/Rl5sJLKu/oWsa38jN/o0cmPCkRsTjqSd78KhXm84txoDx0aDsS3KGXtuA3tuA0tPAQPqFF5PuR7NiQlAkJvxe6v/hpGvYI0IEZUfDCBUITjbAW+3E/t9TN8NNK4E2Kp1QtUOINozr5YGiUQCu4CGsAtoCPdec1BNFourh7ci4+xvyI0JR3bUHmRH7YHEzhlfHxmGnLrTYF+jA1JygI1Xda/343lgQTfj91R/X6YslkdEZCn8fYgqlH61gV2vAFuGG68B0Z55tSwILv5w7fIm/N89g4CPbsCtz6ew8a4JITcD4XvW48k3nZF954TB800po/r7MncEDRFRWWIAoQpFIgEa+4lf3rZGAoihGpAGWgvlhbQSV+YtjpTswue2lerCo98CBHxyG34zT6Ju2z6AoEDSHzMgKOR6z9e3arA2CQMIEZVTDCBUYeWpfSGb2gdk72igSaXC1x90BPrX0X9sUVJydLdJJBLY12iPlz9eD4mjB/IeXUL82peQffMg8hOjkZ/8EPKUx5CnPYGQnYLoZEGnc+m5c+cwZcoUXL58WWMeEEsFkN8ui8OLiYiMYR8QqrCquYuPNT2Ayq6a+4w1b2iHFQ+HUi0WAMDe3ReeQ5cjceN4ZF3ZgawrO3SOmTQXkNi7wKNSVXRoUgMtWrRAk6bNMH3aVMTHx+OX3zbCdcTPcG4+AoBlRsEoBODjw+LzF+sCga7GjyeiiosBhCqst9uJE451qaY7DNdYJ1TtY8tirq98BeDSZhzsqjRH6qGvkHvvFPKTHwCCQu1HgJCTjqT7kfjnfiT++ecf1fkODg7IzspAwi8jkXV5GzwGLkaeokYZlFSTeshJywHAAEJEBjCAUIXlbg/0rqV/n7FhuDKtxJGcrf+4klA2l9gFNoHPmPV6j1HkZkGefB/5SdGY1/AmPlh3BtnX90Fq74Lfdx/EmE9+ROqBxci8sAWZl/7ERw8n43+LPoe/r3eZDcdVqI20yeeoGyIygn1ACoSGhiI4OBitW7e2dlGoHHAyMhGZ9pf3yIbiY1c9k50VV54JzSVSO0fYVqoLx3q9EBISAp8xv6LKF08QOPc/RKM6PAZ8Af93w+FQrzegyMeGn79H1Zp10WrqKsjlcgiCuO7Mx4dKr9zqAYQTnxGRMQwgBUJCQhAZGYmIiAhrF4XKAX1rqFRyFh+1R8LU9QYiJgE/DSq9++fpH/hi0J9RQB2vwtcZeeKjXVBLVJq+D5VCDiOgVmMoMhNx8cfpaN26Nf7cewI7bwC/XRFrXJ4+fYpRo0Zh/vz5SEpKgiBoBgpTaNSAMIAQkREMIEQm+vNl8fG99sDrzYDtIwr3VXIWJzbzcy6de5n75f3uv8CtxMLX0VrryjjU6YbpP56H57BvIHH0wIULF/By/854+uNg5D6+JnYe/fhjbN68GQsWLEDNmjXRZcZqvLBOgex808shZw0IEZmIAYTIRFULRs242gPzugItAnSP2TQccLM377oD6gD1vDW35ZhZA6Ltn1u623IFG7h2eROBH9/ElClTIJVKkXX1L8R+2QQvvzQMP//8MwDALbAOkpOTcWLlNJxe0BG/7Ltk8n0F9gEhIhMxgBAZsKJP4fN+tU07p5Yn8Ennoo/rU0scpnppKrCyP7Cst+b+zDzTy2kq5TVlLr5YtWo1doddg2OTYYCgwF87tkMul6NBx4FwnxUJj6HLIbF3RW70abwxuCXeeecdJCUl6b3u3bt30a1bN7z66qv484/fIcjFKhPWgBCRMRwFQ2TAkPpi8Dh0D+gYZPp5NibE+q7VgNGNC19rr757PMb0+5kqLbfweb4CqFm3Pnxf/xO5jy6j99NvcftGJJpNW4ZdCTZw6zoTTk1fQvKOd5B5cSuWL1+OdevWYdq0aZg2bRqqVSvscbto0SIcPXoUALBp0ybYeNeES6cQJHQdD1T1gjEbNmyAh4cHBgwYUPpvmIjKNdaAEBlhbyOGEHOaVQaaMDOqdidXRwv8KpChFkBiM4DZB8TndoFNsGLlGoSFhaFajcLC23hUhs/43/HR6r1o3LgxkpOTsWTJEtSsWRMvvvgi9u3bh5SUFGzatAkAMGHCBHh5+yA/4Q6Sd87CiHaVMWHCBJw5cwaCoNseExERgTFjxmDgwIH45JNPoFAUr8rkaQZw6kGxTiUiK2IAISpl9jbA1Wni7KqG5hPRHmRjLIB0qFI65UpXCyDT/wHOPS58rRy9om8G2OD2fXD+/AVs27YNPXv2hEKhwN9//42+ffvCw8MDGRkZqF+/PlpP/wlOH9yD14jVsK3cDLk52Vi3bh3atWuH5s2bIzQ0FHFxcarr/vjjj6rnCxcuRJ8+ffDggflJotM64JU/gcP3zD6ViKyIAYSoDLjaAycmaPYjUe+0qlMDYmTekbrehveZQ70J5kqc5j5lfw198598dAioFSqDZ/Oh2L9/P6KiovDWW2/Bzc1NdczkyZOx5KQEUntnuHSYAv/3zmPRxpMYO3YsHBwccOnSJcyYMQMBAQHo1asXVq5ciY0bNwIAJk6cCCcnJxw4cAB169bFRx99hMePH+sWxADlKB0GEKJnCwMIURmRSjT7g7jZae5TZy/Tf42BdYAXqhe+7lUTcDYSVoxJzDK8TyEAj9OAmBTDxxyNFh/r16+PFStW4OHDh1i5ciXmzJmDN954Q+NYiUSCGo3b45dffsHDhw+xfPlytGrVCgqFAgcOHEBISAjS09NRp04drFmzBmfPnkXHjh2RlZWFxYsXo1q1anjttddw+PBh5OebNg6YnV6Jni0MIERlSCOAqPUj0Q4g2uvLKH3USfOL9YeBwBcvFK8sSUamjM9VAO1+Bn6+aPgYuQC8vQ9YW3CMi4sLpk+fjkWLFsHBQXdFvlw5cPoBcOKpF2bOnImIiAi0/fIW3AcsQuv2neDq6opPP/0UEokEDRo0wPHjx7Ft2zZ07NgReXl5+O2339C9e3f4+flh/Pjx2LlzJzIzMw2Wz5TZY4mo/GAAISpDhgKIocChzclW84tVKimcj6Q0xaYXfczuW8D268D8o4XbBAGIeKjZwVUpTwGM/BN4cy9wu2CStMd2teHeaw6mrzyO1NRUjBkzRnX89XgJHlYeigNHTuDs2bOYOHEifHx8kJiYiF9++QVDhgxBpUqVMGDAANSrVw+vvfaaRiDhzKtEzxYOwyUqQ+rrxlT3KHyub6p3fRxtgTaVxeeVC1aWreUpnm/uNOnGPEwt+pinWpUPaTlAo1Xi84nNdY/PVZtMLTYdqG18RC76il1CkKcA3mnXEj/++CNWrVqFsLAwbN++HTt27EB0dDR2794NALh58yZu3LiBnM6hsK/amgGE6BnDAEJUhtRHn3auWvjc1OnN7WWAgw1wear4CACejsDGYeK+ob+XTjkfppl/zl83C59vv667P0ftPWov4KesAZIrgFe3A0GuhfvOPip8bmNjg65du6Jr1674+uuvcebMGYSFhcHd3R0ffPCBuHZTRBvY1eiAywPGIbndCHh4eJj/ZojI4tgEQ1SG1GsBankWPjelyQMo/KJ2dxCH9yq1r6J/KvjiSjDSQVUfuQJIUetT0riS7jHqo25k2n1eCh5vJIj9RLZGFe7LytcMbqpzJBK0a9cOs2bNwqRJk3D+/HmMHTsWkEiRe/ckjn43Ff7+/hg3bhzOnTtn3hsiIotjACEqQ+r9N2xlwIcdxT4cLzWwXpn0STbSQVWfHLnmwnP61q5Rn3fEUJ8XOz2jf849Bl7cXPSolurVq+OXX35B4Pz78HjxS3hUbYicnBz8+uuvaNWqFTp27IgtW7YgL09zXvubN29i9uzZGDFiBGbNmoUTJ07onSiNiMoWAwhRGdKeQXV6K+D4eKCym97Dy8zQ+sCp1wtf96yhuf/PKOjVKgDoUlV3e3a+ZqfP3CICiDZlHjEUMi7Hmd4sZOMeCLfu72PQ8is4ffo0Ro8eDVtbW5w8eRKvvPIKateujWXLluH+/fuYO3cuGjdujC+//BJbt27FsmXL0LlzZ3Tt2hVHjhwx7YZEVCoYQIjKUAt/4M02wNd9ij5W59xSbGJxsQMC1fpZ+LuYdt5LwcCoRrrbvwsH/lbrA5KpJ2yoN8EYChq5Rmo5HpnZL0UBCdq2bYvffvsN0dHRmDdvHipVqoSYmBjMmjULVatWxRdffIHc3Fz06dMHy5Ytw9ixY2Fvb4/jx4/jhRdeQPfu3XHixAnzbkxExcIAQlSGJBLgvfbAsPrmnXdpKrD1paKP+3WIbv8KfZSjbjwLpuswdXXfJn76J0n76SLwn9riuGl6Aki61uJ36pRNMnl6ak6U7qeK/UP+/c+0suYpgNQcsROrv38A5s+fj3v37mHVqlVo2bIlAKBKlSrYtm0b9uzZg3feeQe//PIL/vvvP8yYMQN2dnY4fPgwOnfujN69e+P06dMAAIVCgZCQEHTv3h2fffYZnj59alqBiMgoicDGTw2pqalwd3dHSkqKxlTTRGVt5w3g82PA6oFASzNqP9JygN23gX9uiU0rc4+I2xv4AFHx4vMJzYD5XYGETOBeinj9ait0r2UnE5tTxjQGmvoBIxoCJ2KA0duNl8HVTn8IUd+/bzTQYa34euELwJgmwJmHwIg/9J8zsw2wIlx8fup1zRocdcr30SpAnO31TjIQ2g8YWFfzuNjYWHh5ecHOTv8CPTExMVi0aBF++ukn1eyr/fv3R+PGjfG///1PdZynpycWLFiAKVOmwN7ejFUKiSoAc75DWQNCVE4MrgdETDIvfADiujMjG4q1IS8HF26v4VH4XPkP3dvJ+PW/6gmcnwws7C6GD0B/R1FtxsKHcv+aC5rbUnKAa3H6jwfEoKQUl1H4/FaieG6uHDgeXbhdLojhA9AcIqzk7+9vMHwAQNWqVbFq1SrcunULEydOhEwmw+7du1XhY/LkyWjSpAmSkpLw1ltvoV69eti+vYhkRkQGMYAQlSOmzpBqiHpYUF+JV2riv3RXezGkqDO2UJ45Nl8tfC6RAL3WAwuOGT5e37o0P18Aeq4HBm8Glp8Bxuwo3KfezKP8GLPzgStP9A/rNaR69er48ccfcf36dQwZMgSAWBOyatUqnDt3Dt+FrkQl/wBER0dj2LBhGDZsGB49emT8ohYiCAIePXqE7GwzhzURWQEDCNFzRH3CLxcji98Z4qangsC9lFoZstQmJnuUBjzJ0H+c8n4XYjW3X4gtDCx3k4FfLmnu19fRdfLfwMDNwG9X9N/rSbrhcFK7dm1s374d9+7dw86dOyGVSmFjY4PYBtNh9+5t9J3wEWxsbLB9+3bUr18fn332GdLSijGjWylau3YtKleuDBcXF7z66qtlHkT+++8/+Pv7o1WrVti8ebPJCwcSAQwgRM+tYN/C59X1rB9jo+dfv6uesKE9lLg0GFuZ95POutty5MBVreYaL0fN1/oWozsWIz7+ell337pLQJufgO/PFm47cAd4Z5/m2jbVqlWDjU3hLHC/Xgakdk643mwhzp8/j7Zt2yItLQ3z5s1DrVq1sHTpUiQnJwMAfvjhB7Rr1w4jRozAV199hYsXL5bpnCOrVolz48vlcmzatAmDBw9GUlJSEWeJMjMzERISghUrVphcxl9//RVPnjzBuXPnMGrUKNSpU0ejDw2RMZyKneg5s2uU+AXftjKw7z+grndhfw51jja6fTec9dSAuBjuNlFsxuYI0ReCHqaKnW3VeTpoNtOo14BoN2WpZ62MXODDg4X9RP53Enijtfh84t/iY6Ar8H4Ho28BCgFo3LgxTp48iT/++AOffPIJbt26hffffx+ffvopOnbsiAMHDgAAzpw5g61btwIA6tWrh1deeQWjRo1CvXr19F9bocCtW7fw+PFjxMbGIicnB46OjnBwcICXlxdq1aoFf39/SNTe6N27dxEREQGpVIqNGzdi4sSJ+PfffxEcHIwvvvgCY8aM0dtpdv369bh37x4AYOXKlaryrl+/HjKZ8Q5Ae/fuBSA2UYWHh+PevXuYNGkSvvzySyxYsAAjRoyA1NT2P6pwOApGC0fBUEXR+kfNzp0AcGGKbs0CoH/ETEm8UB04fE//vg1Dix51A4jTv19RqxUJchOH7gLiMONVAwrL3cAH2DtafP7xId0mmeiZ4qPy+OENgGW99d9X/bNQngcAeXl5+PXXX7FixQpcuVJ4gzfeeAPVq1fHsWPHcODAAY1mkebNm2PUqFEYOXIkqlYVZ3wTBAFDhw7Fzp07jb5/Jycn1K9fH02aNEGTJk1w8+ZNrFq1Ct27d8fBgwcRERGB1157DTdu3AAABAYG4u2338bUqVNV/7ddvnwZzZs3h0KhW320YcMGvPrqqwbv//TpU/j5+UEQBDx8+BAeHh5YvXo1Fi1ahPh4cfhVkyZNMGfOHAwfPhy2tqXUmYjKNXO+QxlAtDCAUEXReZ1mDcKw+oYnTFN+6VZy1g0tpqrtBdxOLPq4v18BBm0u+rhanppzkajrW0sczqwsd7AvsKfgu7TGN7orCWsHEFM+C/Xz1AmCgPPnz+OPP/5AlSpV8MYbb6hqKlJTU7Fz505s2rQJ+/fv12iq6NixI0aNGgUHBwdMmjQJMpkMtWvXhr+/PxwcHJCTk4OsrCw8efIEMTExekMDIDbDTJ06FQCQnZ2N7777Dl9//bWqo6y7uzv69+8PT09PnDt3DmfOnFGd27hxY7z88sv49NNP0bhxY1y6dAkSiQS5ubk4ceIErl27hvj4eEilUjx+/BirV69G06ZNcfHiRdU10tLSsGLFCnz11VdITRUTYVBQEGbMmIGpU6fC3d0deXl52LVrF9q2bYvAwED9HzQ9kxhASoABhCqKzVeB2QcLX1+ZZri/x414cVjsrpv6h7iaQrvGQlstT/H+y3oDL/xa9PX8nA13ZNUOII0qAf+MEp/rq80pzQBiqvj4ePz555/YtGkTjh07ptPvYu7cufjss8/0npubm4t79+7h2rVruHz5surHzc0NBw4cgKenp8bxOTk52LBhA7788ktVjYiSnZ0d5s2bh/Xr1+OHH35Ao0aNULVqVaSnp+O7777DrVu3sHbtWlWY0DZ79mwsWbJEZ3tiYiK+/fZbrFy5EnFx4h+8m5sbZsyYgZs3b+KPP/6Aj48P/vjjD3Tt2tXkz43KNwaQEmAAoYpCEIDq3xS+vvdW0cOAZ+4FdtwwfgwgjqYZ2QhYc75wW9vK4sRjhtyeIXaMfZwOtP+56Hs42wIZefr31fUG9o8pDAuNK4l9YwD9AUT53pX7htYHlpdxAFH38OFD/P7779i0aRMiIiJQt25dXLhwAU5OTkWfbAaFQoE9e/YgKioKjx8/xunTp/Haa69h2rRpGse9//77WLp0qcY2Pz8/dOjQAf7+/pDL5Xjw4AGys7Oxdu1aVfORPtnZ2di0aROWLl2KyMhInf1SqRTvvvsuPvjgA/j6+uq5Aj1LGECKITQ0FKGhoZDL5bh58yYDCFUI5n6ZvrMP2Ha96OPaBAJbXy68vpsd0DwAOBqte6y7PfBVL6BPLfF1YhbQ/Iei71GUTcOAUdvE5039gL9eEZ/rCyDXpoudbZX7htQDVvTVf13182/NAM4/FtftMWXCNlM8evQIrq6ucHU1MPWrBTx69AjNmzdHeno6unfvjpCQEPTu3btEHUoVCgV27tyJRYsWISoqCmvWrMG+ffvwyy+/AABsbW0xdOhQTJ48Gd27d2fn1WcUZ0IthpCQEERGRiIiIsLaRSGyuHreph1n6nwiyuO+7w8EugDrhoijbrRNaQFcnlYYPgDAoZTG5inDh7I8j9KA1ef0H9vwe83F79R/K7sRrzsEWGn+EWDkn8BnRiZUM1dgYKBVw4eyDA8ePEBycjL+/vtv9O3bt8SBQCqVYujQoYiIiEBycjJGjRqFdevWYdeuXWjVqhXy8vLw+++/o1evXqhTpw4WL16Mx48fl9I7ovKIAYSoApveUmz2+L9eph1vrIkmUG2FXWUA6V8HODVRnP5d34yq+gJNaQUQdRKJ2KyzyMhCt0vCCp8r64Vz5UDvDcCATUCmnuaeDQWzu64vmGckLgP49AhwM6FUiq0qy414IMfCU2vY2tqW2cgV9XlVBgwYgIiICFy4cAFvvPEG3NzccOfOHXz00UeoXLkyOnXqhKVLl+L27du4ffs2mjdvjqZNm2L58uWq0Tb0bGIAIarAZncUmx8a+5l2vL+L4X3qHVj1XU9fDYi+AGJqLYs5TGloPqdnNnX1WpGMIta7AYBZ/4oztPbbqLtPrhCbr9RHHsWmAyvOAPGZhq+544YYgib8VfT9n2XNmjVDaGgoHj16hLVr16JDhw4QBAFhYWF4//33UadOHTRs2BAXL17E5cuX8c4776By5cro378/vv32W/z3n4nLJlO5wQBCVIFJJObVODRTCxZhE4DVAwpfuzsUPn+pge65pgaQknCzFzuUajM28ZnSAz2zqD9QG/ghF8Qgo6/IyvdxuaCpJl/PCNmdN8Q+NJ3XFW4btwNYdhqYscdwuZSzuIbdN1J4PQRBvO6XYYaPycwTVzvOk5t37bLk7OyM8ePHIywsDDExMfjuu+/Qo0cPyGQy5Obmonnz5vjmm2/QsmVL5ObmYs+ePXjrrbdQu3Zt1K1bF9OnT8eGDRtw79491ciie/fuoWbNmqhduzbef/99nD592uAwZrIczoRKRCbrUUPst1HHC6jiJv4oudgBa18Uv6jr6ulT4qCnNt/ewP9AX/cGQs+KnUf/jDK9fKk5Yqha0QeYua9we7KZS6IoK0zUJ0QbvEWssdDHlBCnvbYNAFwvaKo59cDweXbF/DXx4hPg74Ih0x901H/Mm3uAA3eBN9sA77Uv3n3KUlBQEEJCQhASEoKkpCSEh4ejc+fOcHJywptvvolr165h9+7d2L17N06cOIFbt27h1q1bqinpK1eujK5du+LatWu4e/cuAGDp0qVYunQpPDw80LlzZ3Tp0gXdu3dHs2bN9PZz2bVrF8LDw9G7d2+0b9++yNlhyXQMIERkMokE+FhrrZaXGwBbo4AZrcXRIIboqwEZ20T/scMaiD8/ngf+LEY5h9QH7iUDXxfMsZWSY/RwHfkKIEurz4eh8AHof2/afJ01r69vLR59bIv5fZerVqshCPr77xwQv5Ox5nz5DCDqPD090aeP5tjohg0bomHDhnj//feRmpqKQ4cO4fjx4zhx4gTOnz+Phw8fYuNGsT3M29sbS5cuxb59+/DPP/+oOtj+/bc4/76Xlxe6d++OHj16oGfPnqhVqxauXbuGYcOGIS8vD59//jm8vb0xYMAADBo0CD179oSHh4elP4bnCgMIEZXIV72AT7oAHg7Gj/PVmtLi/3oVfY65HVLVh8Kqh6FcI00MrzQENl/T3JadDzw10i9DmzKAGGtRUl9V+GkGEGDiQBdTg4o29bLkK4wHmeznYO04Nzc3DBkyBEOGDAEAZGRk4MyZM9i7dy8iIiLw+eefo1OnThg/fjzy8/Nx4cIFHDt2DEeOHMHRo0eRmJiIP/74A3/88QcAoGrVqpBKpcjLy0Pt2rWRkJCAhIQE/Prrr/j1118hk8nQvn179O3bF/369dOoQcnJyUGPHj1w9epV9O3bF4MHD0avXr3g4+NjrY+nXGIAIaISkUiKDhKAWKOhPvOqvkXntJkTQF6sC0xoVvjaU8+aNvr8r6duADl8T7OvRlFMWbBPvV9IQpbpAcRWK4AoBNP6zqjXeOQVEUD0kSvEZpxGvoabysozZ2dndO/eHd27d9fZZ2Njg9atW6N169aYNWsW8vLycPbsWRw4cAAHDx7EyZMnERMjLqXs5uaGI0eOwM/PD2FhYdi5cyf27NmD69ev48SJEzhx4gQ++eQTVKpUCX369EHfvn1x4cIFhIWJnW+2bNmCLVu2AADq1q2Ljh07okOHDujYsSPq1atXoec7eQb/WhHRs8hOBoxrKo4SAQBXE760zQkg3/bTfO1lQigqrU6w1xOAI/cM17T8dQP4Q20S0El/AztHmnZt9eBwL1nsi/J6M2BmW+Pnqb+1XDngZOaI2mWnge8ixGCn/dk+b2xtbdG+fXu0b98ec+fORUZGBk6cOIGwsDD06tULlStXBgB07doVXbt2xbJly3Dv3j3s27cPe/bswcGDBxEXF4f169dj/fr1quv+73//UzX1XL16FTdv3sTNmzexdu1aAGKzT6dOndCtWze88MILaNKkCRYvXoyNGzeqJmWrVq2aVT4TS+BMqFo4FTtR2Zl9oLC24cxE48N6AeDAHWDi36ZdW3sm1+x8oF6o8XOkEuDuW6W/2q96ee4k6V/bpms1zZlhlcfn5Is1JIEFNSRv7RVH0ABiJ+CDdzWPT88Vw4V2mDr7CBi+VXweMUlcSFBbrW8La2a0P7/a34o1J/r2kabc3FycPHkSe/fuxd69e3Hp0iWMHj0av/32m+qYpKQknDp1CidPnkRYWBjOnDmDrKwsjet4enoiKalwhUWJRILevXvjpZdewuDBg5+JqerN+Q5lDQgRWUzk08LnRYUPAHAuopbERip+8a7qr7vPwUasBVD/DauaOxCtNg+H9qq4AS7iWjSlaavu8icADI98GbZVnHl132igvo9mE0yqVmfamBSxqahrNeDXIZr71Jt8lMNss/KAVefEmWeDfQEvR8OrGxe1LhAVsrOzQ7du3dCtWzcsWbIE6enpOuv4eHp6on///ujfX/zLmpeXhwsXLuDo0aM4evQoDh8+jKSkJMhkMrz//vuIiIjAwYMHsW/fPuzbtw9Tp05Fly5dMGDAALRo0QKBgYFISEjA2bNn8fTpU/To0QMvvPCCNd5+sTGAEJHFJJk5HNZFT7PB8AbAtJZAbS9xdEdKjvhFqs/8bsC8I4WvfxsK2MuANj9pHjenI7DrltisMcnEGhdTxKYbnsbdUHON8vh+G4EjYzWbYNK0AsjvBeFGe42dzDyx5kVJWZOx/IwYQJafEWs1fJwKA8igTUC/2sAbrQ3Pd1IciVliDU1ZzHBbXrm4FJ2ubW1t0aZNG7Rp0wbvv/8+srOzcfToUfj4+KBly5YAgNu3b+P333/Htm3bcO7cORw5cgRHjhzRe71Fixbhjz/+wLBhw0rzrZSpCvRXgoisbVF3YNZ+YLFuv0C91Dt3/jIYeJIBDKijtl1iOHwAgI3Wt2hVd/HR30UMB7UKVq2f1kr8MRQWimPff8CUXeadcyux8LlCALr8ojkKJk1rQjVD3RcHbATuJBe+VoYd7VoXD7WOwJfjxJ9xTcWZV3NKYXKyhEygxRpxBNTZySW/3vPMwcFBZ5hx7dq18dFHH+Gjjz7CvXv3sG3bNpw4cQKXL19GYmIiHBwc0KZNG2RmZmL//v0YNWoUXnrpJTRr1gz+/v4ICAiAj48PvLy84O3tDScnJ0jKUdUWAwgRWUyXamJ/BFOpBxBfZ6BbdfPuJzPwDf3bUCA0QpyAS11p/pY++4D55/Rcr7tNvSnlodpsrSnZwIpw/ddRDx9AYQ1IhtbcJvo6AP7fKc0ZYEsivGB6e3OGNJN+1atXx7vvvot3331XZ19+fj5eeeUV/Pnnn9i4caNq7hNt9vb28Pb2hpeXF3x9fVG3bl00atQIgwcPRlBQUFm/BR0MIERUbqkHkPxi/EZuaJRLHS9geR/d7aU53NSc5iZThjFra7Ja/3Z9c3ooa0C017PR7gMDAD9d1N224Cgwr2vRZcrKEzvFKidd4xAHy7CxscHWrVtx5swZ/PXXX7h//z5iY2MRGxuL+Ph4JCQkIC8vDzk5OXj06BEePRKT4eHDhwEAwcHBDCBEROrUayRyi7F0h74vWGPsLTDLdlV3zQXpAHGq+C9Pls719c3YquyEql0DIjfxM/35omkBpOsvYjNZ+ETAz0WzhsXQbKxUOiQSCdq1a4d27drp7BMEARkZGarJ1BISEhAbG4uoqChcu3YNjRo1skKJGUCIqByTSMQRG3eTxXVhzJWoNspxYrOijzenBqSpH/Dny8C6S+JqtqvOmXZeSCtgwTGxo6i60AjT723MQz2L6k36GzgxQbcGRG5GQDMlQDwp6NAa9gAYVl9zX468YnVELU8kEglcXFzg4uJSruYV4V8HIirXfhhY/N+e1fsefGrCb/Dm1IB83FkcoTK5hViTcCwaiIwv+rxKzrrhozQ91hNAUnKATw7rBg5Ta0AA4wEiJx+4maj5GtBsgsllACEtFXcOWCJ6ZhS36r6au3nHmxNA1PuXyKTASj1zkejjq2dCsNJyN6lwhV1tysnM1JlTA5KTLwaKUX8CY3dohov39gMDNxW+VvZDUWgFkLJQVtelssc8SkTPrVcbibUNXUysdVYPOsMbAN6OwA/n9R+r3cHV0cSpzvXNSFoaopOBbnpmXDXGnD4y2fniz8mCobypuYUL7P11U/dYQDMclEVQWH4a+CYc2PkK0LiSuO1phtjXpbpH6d+PShdrQIjouWVvA4S0LvxyMoeDTGxmaWBgAVOZdgAx8dc5b0fg6z6Amz3w84vml8uQA3fNOz47X3diM2MWh2l2BO63Adh8VbOfjfq1Ac25RJQBRPn443lgjVq4e5ohzuq64ozpZfr6jFiL88Wxwm2tfhQ7wz41MMMrlR8MIEREeiibJ8Y31b/flBqQjkG6q9naSMUOmpenAt1KsT9gem7Rx6jr9gvwQE9/EUO2Xwc6rS18/TBNXN34ip7J27IKAoj61Ps5+cCFWKDBSuDzY8Dnx4EvjheW+/tz4uigZaeBT4+YN4Q3X09fFvVJ3ah8YhMMEZEeygAysqHYb0OuEIejKmcT1Q4g2kHDyxHYWDAr9oSdwKF7mvslEt1alJIIf2je8aW15s3YHbrbVp8ThxZvuVa4LVcObIsSw8KPFwq3Z+aJ872oN9H8cgnoXxtoV8W0MigDiHqnWg75Lf9YA0JEpIeyf4REIq5C27uWuHaKknYA0f7Cq6R27IRm4mPXMhwBeeK+aceVZugxRj18AGJzjHKFX3WtfwQ+PAisv6y5Xd+EaoYom4bUQwzzR/nHAEJEpIe+Iarq67IU9UXup7YeWZdqwMHXxCHFJbFhaOHzJT1099fw0N02TqsJyVpDYXPlhVPCa9t0VXebOXOyKP+s1PuclEUNiEIAop6aN3yZDGMAISLSQ98QVWe1fh5FfcE10Zo4rbaXaV/+7Srr3/52W6Ct2r46XrrHtAwAXO00tw2vL25XKs3p5s2RIzdvJIx2k5Yx+XoCSFmEhG/Dgb4bxT4qVHIMIEREagbXEx+ntNDd92K9wudFBZAZrYt3/xdq6N/uYqdZA+Nmr3tMl2rAsfHAu2qzcfu7aA63NXWukxYB4kyvV6YBf7+i/36vNDTtWkBBDYgZAURZ5P+SxJWFjVEFELVmG0O1LSWx7LT4+NuV0r92RcQAQkSkZkUf4PI03RoMAGgTCLxYV/xyrq5nkrNxTcUv6tOvF6+pY/erhXNraJNJxNAT0kqc30RfDUhzf7Hza6vAwm0+TpojSkztfBrgIl7HzV78LPQFl1p6ymBIrpk1IHIFMPcw0P1XYMou4ESM4WPz9fQByZWLI2x6rhdH3RhyIgZ4e5/YabY4rjwR5yMxp88KiTgKhohIjURiOARIJMC3/Qyf+1k34NMumjUVprKXAQ19gZsGZjKVFlzzg46Gr6FcVbdNINAqAKjjLc7Sas6Mp0rafVz0vScnM75BbiboLsJnTL4C+FWtY+qZh0CnqoaPBXTnHfnnljgc91YiMK0lEJOq2Rz18wVxXR5ArGH64gXjZZJKdCdvG7hZfLSRAjPaFP2+qBADCBFRKSpO+AAKQ4KhJhJTLqvs/2ErA/4cUbjd3FWBAd33YaunXKbMNtrcX5z/45tw8+6vPbfHN+FAxCNxccJbCZrlUa7yq94EkyvX7EfS6kfx8c+XxZqdR2mF4QMAnphQMyTTE0CUTFkHyFwpOcCbe8RmweENSv/61sYmGCKickDZadJQAJGZ8L+1oX4pk5qLjz3U+pc4FzF1vPb9fJ10j9HXTFXNXQwJSi52useYQl8n0lMPgPlHgQ1XxVWIlZSTmWk3wTjruffwrcCfUbqzwJrSOdfYn0FZDPv9PgI4Gg28+28ZXLwcYAAhIioHlL9YV/Mo3DatZeFz7XlHzDG0PvDvaGDVgMJtfkWsSaN9v696ab5+vZnYP2TLcM3tg+pqzvBa3ABSnE6k6k0wxjq8vvuvbrOUKZ1zjQ29LothvylmTJX/LGIAISIqR2p7AaH9xC/2ofULtxcVQP54yfA+iQSo5wPYqX3JNqoEhE8EFnfXf87DVM3XtTyB+t6Frz/tIj62qwKsUZvfpK635nnFDSBJZnYK3XQVmKVWU1BUp9fBWzRfKwNIcjaw+5Zmc46S0QBielFN9rxPpsYAQkRUzgysK36xq/exMDZKw14GtDYwf4i2P18GRgQDC7qJk6X1MDDs97qePg2vNBIfm/lp/sav3h9De/E+cxbpU/fhQdPOUz/+aWbh66ICiPY+exsgLgNouhqYvrtwyK06qQnfmMtOGR91E5MCvL8fuG3CWjXP+3TyDCBEROWU+lBefSNIZrUXH/XNimpIq0CxOcWr4Au/koGmmMpuutvGNRXXt1k/VHN7C39xxeGJzXRrQOxMnHfE0Rb4a6Rpx5oiV2HesF97GfDS1sLXf0bpHmNTRCDIkwMrwsW1btZfBoZs0Q0a43cCv0cCo7cXXSZ9ASTiETBwE3D2UdHnl3ccBUNEVI55OwIJWUAbPTUcb7UBxjUB3B2Kf32JBDg2Dujyi/h6RmtxrpDprXSPlUrEFX61uTsAu0bpv76pE59JJUBTf7Hm5/QD084xJldu3twcDjZAtFrIy5GL86fkKYDvz4pf/Jla11OfX0Ui0eyD8slh8fHtfZqfzX9J4mOsCaNu9DW7KUPSq9uAmzOKvkZ5xgBCRGRFM9uIvzUrazO07RsNXI4DXqiuf39JwoeSesfXWp7A+x1Kfk0l9dElqweIfTviMnSbOJTDYFNL2PHSzxl4kiFOm14SqTlA9W+MH5OjVcOir9/IlTjgbhJQw1PsW2IOY/1+tO/9LGITDBGRFb3TDjg+HnjTwNTtvs5iP42SjIIxh76hq+byUuvPod4EU9cbGNUImNlW9xzlF6qhABLsI47k0Wdel8Lnlhp10+s34L5aR10JDIeCbr+Kj9N3m3eP0vojL848MJbAAEJEZEUSCVDV3fodDud0BPrXBnoa6JRqjt61gDGNgf/rpRlATJmkzVAA2f2qOJLHU0+Nj/p8JKU574gxNxOAd/YVvs4vos9JRq7ma1spcCkWqLZC/DnzUPec0vg7cT8VaPEDsPRUya9V2hhACoSGhiI4OBitWxdzBSkiomfYtFbA9wNMm/CsKFIJsLA78FKw6QGkiqv4qB5A3lDrh6L8Ml6s1eG2qrtmM09xA8j358w/50pc4fMcuf4mGKXg7zVfO9gAb6jViIz4Q/cc9fyhLyB9dgyITjZexi/DxGavkjZJlQUGkAIhISGIjIxERESEtYtCRPTcsC8igNTwAL7uA2warrtPe2guAPSrDZybXLgY37gmmvcobgApqZx880bdONgUTiFviHqzm75r/3RB7Dz8xXHDHW7Tc/VvLw/YCZWIiMqMTREBxFYGDKuvu125Tx8fJ+CXwcDph+JkbQ/U+mKoB5CJzcVwsvKs/uss6WH+fCOGZOebN+rGx8nwysQxKcChe5rr4SwJE6e512fNefHY/rXF4dCOatPsZxYRcqyJAYSIiMqM+uyh+gKI9twafWoB+/4TO6sam0OkshswvGCuEkM1IPW8gZENDQeQfrX1j8gxR4CLGCTCHwEv6WlGMcRXTwBZfhroXgP46iRwLEZzn/raN/qsvSj+AOLw7Hfbic1WRdWyWBMDCBERlZkiA4jWtmW9gRMxQLfqYrPGwuNA2yJmeVXvA6I+eVtRnV5tpcVfvVh1bxPnOdF27anuir9fnxF/SuqbcPEz61RVt/NrecI+IEREVGYkRQUQrS9wFzugb20xSLg7AOenAD8OMn4P9RBgq3aPIgOIzHjH0deaAM39dberTyzmUMxf4xOyyrZ/xsM08VHfgnZHo/XPrGtpDCBERFRmDNWAKPt9GJr/RMlOVvRwVPWmGkcza0BS1ULA72oL+vWpBXzQQdw2uJ7meeqL8tmX03aErHxx/o+ErMJt0clA79+AsTuAzuusVDA1DCBERFRm1If1qo/qWNYbODtJ7PNQGvcY3UgMDQ18C7cra0MMrZUjkWgO+1UPLyGtADd7Mdx801erlkXtuTlNMC/WNf3YksrMBQZs1NzW5RfgRoLlylAUBhAiIiozhmZwlUjEWV5Ly6IewA8D9fcBGdUI8FCbwGxAHWBKC/F5mloA0ThXK1i42eu/r3YTjPZifOpeCga+62d4f2mKigci9axoXJ4wgBARUZmx1BTySs5qQ1DV+4Ood/hc2R/4uLP43FAHVlutb8dv+orDYH8ZrLldvflnVCNgz6uGp1C3kxVvnhJ9/VCK8tfNoo8xZ9hwWWAAISKiMtOhClDTQ2wesQQntQCiXouRZ2CSsA87il/w3/bVbILRDk4dgoBj48XROerUA4wUYq2LoaVX7GS6w45NMaeT+eeYosFKYMf1srm2KRhAiIiozNjbAAfHiivhWoL6JFzqnVANLTZXxQ3YMRJ4sZ7muaYu4KZea1LUcjJpOZp9Yta+qHvMkHriHCHqYSjYx/A1baRAqwCTiqpDIQAz9xV9XFlhACEiojIllVhusT0ntS9u9RE477QTH0c1MnyuepgwdXVc9SYYQwvaVS5Y56apn2YoqqTVB+aDDsCKvsDZycD4poXbXQ30PwGAsAlAoKvh/SFFjDIq7jDi0lBOBxARERGZz1mtj4V6iJjRGuhVw3gnUfVwUNXNxPuZUGtyaKw4Jbqno2b/EPUAMq2lZlgY1xT49w7wipHA5GQL+LuIQ24NGdsECDWyxJmPnvV2LIUBhIiInhv2Bvp9SCWaQ3QNuTxNnJzMWK0DAMzrAvx5XQw2P14QtxkKIA42hTUNmWphwVNtZI72ujcBrmJwMUb5Xg3Ndjq2SdHDhH2cjO8vS2yCISKi54Z6U09xmhfc7XWbRvR5vTnwzyixVkNJXhBAtr6k/xxAMyzYmtB8Y4yyiclQDYi9TdGTsRUVtMoSAwgRET1XFnUXV8JtWczOmcWlrAFpU1m8vz7tqoiPNT00t2uvC2OK+IJZTg0tOGcnKzqAGJuKvqyxCYaIiJ4roxtb577qTTCGajS8HMVmHietb19zAkiXquJquf1qi68zDTTByBWao25mtQf+75TmMcb6j5Q11oAQERGVAvXQEeBi+Dh3e90+H+YEkO/6AfO7ijU9ADCrg/7j0nI0a0Aa6ukDY83JyFgDQkREVArUa0DGNwPupwI9a5p2rjl9QNwdgAnNCl8Pqw809AF6b9A8Li1Xc0I1Rz3f+KwBISIiesa5q41qcbABFnYHXqhu/BzlGjVFLco3sI74OMlA35J6PsCxccDp1wu3pWs1zdTy1HwtlVh+qnx1rAEhIiIqge/6ARuuiBOJmevQa8CtRKBtZePH/V9vsW9L60DDx1TzEB9rewG3Ewv7iOwfI9aG+Kk1C7nZA5enWm6COH0YQIiIiEpgUF3xpzi8ncSfojjYiOvRmGLby8CVuMLj9U2+JldYN3wADCBERETPFXcHoFNV48cUZ9hvaWMfECIiogqGAYSIiIgsTm7iar9liQGEiIioglAO353V3qrFAMA+IERERBXGp12AVxsBdbysXRIGECIiogpDKtE/KsYa2ARDREREFscAQkRERBbHAEJEREQWxwBCREREFscAQkRERBbHAEJEREQWxwBCREREFscAQkRERBbHAEJEREQWxwBCREREFscAQkRERBbHAEJEREQWxwBCREREFscAQkRERBZnY+0ClDeCIAAAUlNTrVwSIiKiZ4vyu1P5XWoMA4iWtLQ0AEBQUJCVS0JERPRsSktLg7u7u9FjJIIpMaUCUSgUePToEVxdXSGRSErlmqmpqQgKCsL9+/fh5uZWKtd8lvHz0MTPQxM/D038PDTx89BU3j4PQRCQlpaGwMBASKXGe3mwBkSLVCpFlSpVyuTabm5u5eIvSHnBz0MTPw9N/Dw08fPQxM9DU3n6PIqq+VBiJ1QiIiKyOAYQIiIisjgGEAuwt7fHvHnzYG9vb+2ilAv8PDTx89DEz0MTPw9N/Dw0PcufBzuhEhERkcWxBoSIiIgsjgGEiIiILI4BhIiIiCyOAYSIiIgsjgHEAkJDQ1G9enU4ODigbdu2CA8Pt3aRSt3ixYvRunVruLq6olKlShgyZAhu3LihcUx2djZCQkLg7e0NFxcXDB8+HE+ePNE4JiYmBgMGDICTkxMqVaqE999/H/n5+ZZ8K2ViyZIlkEgkePvtt1XbKtrn8fDhQ4wZMwbe3t5wdHRE48aNcfbsWdV+QRDw6aefIiAgAI6OjujZsydu3bqlcY3ExESMHj0abm5u8PDwwMSJE5Genm7pt1Jicrkcc+fORY0aNeDo6IhatWrh888/11g/43n+PI4dO4ZBgwYhMDAQEokEO3bs0NhfWu/98uXL6Ny5MxwcHBAUFIQvv/yyrN9asRj7PPLy8jB79mw0btwYzs7OCAwMxNixY/Ho0SONazyTn4dAZWrz5s2CnZ2d8PPPPwvXrl0TJk+eLHh4eAhPnjyxdtFKVZ8+fYS1a9cKV69eFS5evCj0799fqFq1qpCenq46Ztq0aUJQUJBw8OBB4ezZs0K7du2EDh06qPbn5+cLjRo1Enr27ClcuHBB2L17t+Dj4yPMmTPHGm+p1ISHhwvVq1cXmjRpIsycOVO1vSJ9HomJiUK1atWE8ePHC2fOnBHu3Lkj7Nu3T7h9+7bqmCVLlgju7u7Cjh07hEuXLgkvvviiUKNGDSErK0t1TN++fYWmTZsKp0+fFo4fPy7Url1bGDVqlDXeUoksXLhQ8Pb2Fnbt2iXcvXtX2Lp1q+Di4iKsWLFCdczz/Hns3r1b+Pjjj4Vt27YJAITt27dr7C+N956SkiL4+fkJo0ePFq5evSps2rRJcHR0FFavXm2pt2kyY59HcnKy0LNnT2HLli3C9evXhVOnTglt2rQRWrZsqXGNZ/HzYAApY23atBFCQkJUr+VyuRAYGCgsXrzYiqUqe3FxcQIA4ejRo4IgiP+IbG1tha1bt6qOiYqKEgAIp06dEgRB/EcolUqF2NhY1THff/+94ObmJuTk5Fj2DZSStLQ0oU6dOsL+/fuFrl27qgJIRfs8Zs+eLXTq1MngfoVCIfj7+wtfffWValtycrJgb28vbNq0SRAEQYiMjBQACBEREapj9uzZI0gkEuHhw4dlV/gyMGDAAOH111/X2DZs2DBh9OjRgiBUrM9D+wu3tN77ypUrBU9PT41/K7Nnzxbq1atXxu+oZPQFMm3h4eECACE6OloQhGf382ATTBnKzc3FuXPn0LNnT9U2qVSKnj174tSpU1YsWdlLSUkBAHh5eQEAzp07h7y8PI3Pon79+qhatarqszh16hQaN24MPz8/1TF9+vRBamoqrl27ZsHSl56QkBAMGDBA430DFe/z+Ouvv9CqVSu8/PLLqFSpEpo3b441a9ao9t+9exexsbEan4e7uzvatm2r8Xl4eHigVatWqmN69uwJqVSKM2fOWO7NlIIOHTrg4MGDuHnzJgDg0qVLOHHiBPr16weg4n0e6krrvZ86dQpdunSBnZ2d6pg+ffrgxo0bSEpKstC7KRspKSmQSCTw8PAA8Ox+HlyMrgzFx8dDLpdrfIEAgJ+fH65fv26lUpU9hUKBt99+Gx07dkSjRo0AALGxsbCzs1P9g1Hy8/NDbGys6hh9n5Vy37Nm8+bNOH/+PCIiInT2VbTP486dO/j+++/x7rvv4qOPPkJERATeeust2NnZYdy4car3o+/9qn8elSpV0thvY2MDLy+vZ+7z+PDDD5Gamor69etDJpNBLpdj4cKFGD16NABUuM9DXWm999jYWNSoUUPnGsp9np6eZVL+spadnY3Zs2dj1KhRqsXnntXPgwGESl1ISAiuXr2KEydOWLsoVnP//n3MnDkT+/fvh4ODg7WLY3UKhQKtWrXCokWLAADNmzfH1atXsWrVKowbN87KpbO833//HRs2bMDGjRvRsGFDXLx4EW+//TYCAwMr5OdBpsnLy8OIESMgCAK+//57axenxNgEU4Z8fHwgk8l0RjY8efIE/v7+VipV2ZoxYwZ27dqFw4cPo0qVKqrt/v7+yM3NRXJyssbx6p+Fv7+/3s9Kue9Zcu7cOcTFxaFFixawsbGBjY0Njh49im+++QY2Njbw8/OrUJ9HQEAAgoODNbY1aNAAMTExAArfj7F/K/7+/oiLi9PYn5+fj8TExGfu83j//ffx4Ycf4pVXXkHjxo3x2muv4Z133sHixYsBVLzPQ11pvffn6d8PUBg+oqOjsX//flXtB/Dsfh4MIGXIzs4OLVu2xMGDB1XbFAoFDh48iPbt21uxZKVPEATMmDED27dvx6FDh3Sq+lq2bAlbW1uNz+LGjRuIiYlRfRbt27fHlStXNP4hKf+haX95lXc9evTAlStXcPHiRdVPq1atMHr0aNXzivR5dOzYUWdY9s2bN1GtWjUAQI0aNeDv76/xeaSmpuLMmTMan0dycjLOnTunOubQoUNQKBRo27atBd5F6cnMzIRUqvnfr0wmg0KhAFDxPg91pfXe27dvj2PHjiEvL091zP79+1GvXr1nrvlFGT5u3bqFAwcOwNvbW2P/M/t5WK37awWxefNmwd7eXli3bp0QGRkpTJkyRfDw8NAY2fA8mD59uuDu7i4cOXJEePz4seonMzNTdcy0adOEqlWrCocOHRLOnj0rtG/fXmjfvr1qv3LYae/evYWLFy8Ke/fuFXx9fZ/JYaf6qI+CEYSK9XmEh4cLNjY2wsKFC4Vbt24JGzZsEJycnITffvtNdcySJUsEDw8PYefOncLly5eFwYMH6x162bx5c+HMmTPCiRMnhDp16jwTw061jRs3TqhcubJqGO62bdsEHx8f4YMPPlAd8zx/HmlpacKFCxeECxcuCACEZcuWCRcuXFCN6iiN956cnCz4+fkJr732mnD16lVh8+bNgpOTU7kchmvs88jNzRVefPFFoUqVKsLFixc1/n9VH9HyLH4eDCAW8O233wpVq1YV7OzshDZt2ginT5+2dpFKHQC9P2vXrlUdk5WVJbzxxhuCp6en4OTkJAwdOlR4/PixxnXu3bsn9OvXT3B0dBR8fHyEWbNmCXl5eRZ+N2VDO4BUtM/j77//Fho1aiTY29sL9evXF3744QeN/QqFQpg7d67g5+cn2NvbCz169BBu3LihcUxCQoIwatQowcXFRXBzcxMmTJggpKWlWfJtlIrU1FRh5syZQtWqVQUHBwehZs2awscff6zxhfI8fx6HDx/W+//FuHHjBEEovfd+6dIloVOnToK9vb1QuXJlYcmSJZZ6i2Yx9nncvXvX4P+vhw8fVl3jWfw8JIKgNvUeERERkQWwDwgRERFZHAMIERERWRwDCBEREVkcAwgRERFZHAMIERERWRwDCBEREVkcAwgRERFZHAMIERERWRwDCBGVqoyMDCxatAgtWrSAi4sL7O3tUaVKFXTu3Blz5szBf//9pzq2evXqqF69uvUKS0RWY2PtAhDR8yMtLQ2dOnXC5cuXUbt2bYwZMwbe3t6Ij49HeHg4lixZglq1aqFWrVrWLioRWRkDCBGVmuXLl+Py5cuYNGkSfvjhB0gkEo39d+/eRU5OjpVKR0TlCZtgiKjUnDp1CgAQEhKiEz4Acan1+vXr4969e5BIJIiOjkZ0dDQkEonqZ/78+RrnHDt2DIMGDYKPjw/s7e1Rp04dfPLJJ8jMzNQ47siRI6rzT5w4gW7dusHV1RUeHh4YPnw4bt++rVOeW7duYcKECahRowbs7e3h5eWFpk2b4u233waXySIqW6wBIaJS4+3tDQC4efMmmjVrZvA4Dw8PzJs3D8uXLwcAvP3226p93bp1Uz3//vvvERISAg8PDwwaNAiVKlXC2bNnsXDhQhw+fBiHDx+GnZ2dxrVPnz6NxYsXo2/fvnjzzTdx7do1bN++HcePH8fp06dRs2ZNAMCjR4/Qpk0bZGRkYMCAARg5ciQyMjJw69YtrFy5EkuXLoWNDf+LJCozVl2Ll4ieKzt37hQACK6ursKsWbOEffv2CfHx8QaPr1atmlCtWjW9+65duybY2NgITZs21bnG4sWLBQDC0qVLVdvUlzRftWqVxvGrVq0SAAgDBw5Ubfvmm28EAMLy5ct17p2QkGDK2yWiEmATDBGVmhdffBH/93//B0EQ8H//93/o06cPfHx8ULt2bcyYMQO3bt0y+VqrV69Gfn4+vv32W1XNitIHH3wAX19fbNq0See8unXrYvLkyRrbJk+ejDp16uCff/7B06dPNfY5OjrqXMPLy8vkchJR8UgEgQ2dRFS60tLSsHfvXpw8eRJnz57FmTNnkJeXBwcHB2zZsgUvvvgiAKiG4N67d0/nGm3btkV4eDg+/vhjvU0ha9asQUpKCtLT0wGIfUBeeOEFTJgwAT///LPO8RMmTMC6deuwf/9+9OzZE/fu3UOjRo2Qk5ODYcOGoW/fvujatauqiYaIyhYbOImo1Lm6uuLll1/Gyy+/DABISUnBRx99hJUrV2LixIl4+PChTt8NbYmJiQCAhQsXmnVvPz8/o9tTUlIAiOHn9OnTmD9/Pnbv3o3ff/8dAFC/fn189tlnqrITUdlgEwwRlTl3d3d89913qFatGuLj43HlypUiz3FzcwMApKamQhAEgz/anjx5ovd6yu3u7u6qbY0aNcIff/yBxMREnDp1Cp9++iliY2MxcuRIhIWFFeetEpGJGECIyCIkEgmcnZ01tslkMsjlcr3Ht23bFoA4qsUcYWFhUCgUGtsUCgVOnjwJiUSCpk2b6pxja2uLdu3aYcGCBfjmm28gCAJ27dpl1n2JyDwMIERUalavXo2IiAi9+3bs2IGoqCh4eHigUaNGAMTOnvHx8cjOztY5/o033oCNjQ3efPNNxMTE6OxPTk7GhQsXdLbfvHkTa9as0di2Zs0a3Lx5EwMGDICvry8A4Ny5c0hNTdU5X1lT4uDgUMS7JaKSYB8QIio1e/bswbRp01C7dm107NgRgYGByMjIwIULF3D8+HFIpVKsXLkS9vb2AIDu3bvj7Nmz6NevHzp37gw7Ozt06dIFXbp0QaNGjbBy5UpMnz4d9erVQ//+/VGrVi2kpaXhzp07OHr0KMaPH49Vq1ZplKFPnz546623sHv3bjRs2BDXrl3D33//DR8fH6xYsUJ13Pr167F69Wp06dIFtWrVgpubGyIjI7F79254eXlhwoQJFv3siCocKw3/JaLn0PXr14Uvv/xS6NWrl1CjRg3BwcFBcHBwEGrVqiWMGzdOOHv2rMbxaWlpwuTJk4WAgABBJpMJAIR58+ZpHBMeHi688sorQmBgoGBrayv4+PgILVq0ED788EMhKipKdZxyHpB58+YJx48fF7p27So4OzsLbm5uwtChQ4Vbt25pXPf06dPC1KlThUaNGgkeHh6Co6OjUKdOHWHGjBlCdHR0mX1GRCTiMFwiei4oh+HOmzdPZzp3Iip/2AeEiIiILI4BhIiIiCyOAYSIiIgsjn1AiIiIyOJYA0JEREQWxwBCREREFscAQkRERBbHAEJEREQWxwBCREREFscAQkRERBbHAEJEREQWxwBCREREFscAQkRERBb3/yXXqwhYBVlIAAAAAElFTkSuQmCC\n"
},
"metadata": {}
}
]
}
]
} \n"
],
"metadata": {
"id": "d5swkZB6PnNA"
}
},
{
"cell_type": "code",
"source": [
"from IPython.display import HTML\n",
"\n",
"HTML(f\"\"\"\"\"\")"
],
"metadata": {
"id": "VOPjmHWg2oQq",
"outputId": "8c4c0278-40ce-4345-c561-dd6df7d25fe5",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 321
}
},
"execution_count": null,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"
\n"
],
"metadata": {
"id": "d5swkZB6PnNA"
}
},
{
"cell_type": "code",
"source": [
"from IPython.display import HTML\n",
"\n",
"HTML(f\"\"\"\"\"\")"
],
"metadata": {
"id": "VOPjmHWg2oQq",
"outputId": "8c4c0278-40ce-4345-c561-dd6df7d25fe5",
"colab": {
"base_uri": "https://localhost:8080/",
"height": 321
}
},
"execution_count": null,
"outputs": [
{
"output_type": "execute_result",
"data": {
"text/plain": [
"