7. Lesson 7: Behler-Parrinello Gaussian Process Regression (BP-GPR) for Machine Learning Potentials#
\(\Delta\)MLP with PyTorch for the Claisen Rearrangement reaction
For this tutorial, we will be combining the Gaussian Process Regression (GPR) from Lesson 2 and the symmetry functions from the Behler-Parrinello and ANI models from Lesson 4 to train a \(\Delta\) Machine Learning Potential (\(\Delta\)MLP) model to reproduce the energy and forces for the Claisen Rearrangement reaction. With a BP-GPR, we can use the BP symmetry functions for feature extraction and the GPR kernel for predicting observables. The goal of this model is to train with data that is from semiempirical (PM3) and DFT (B3LYP) levels of theory. The BP-GPR model will be used to correct the semiempirical values to obtain DFT level accuracy, that makes it a \(\Delta\)MLP model.
7.1. Importing PyTorch Lightning and Libraries#
We will first install PyTorch Lightning and import libraries needed to train our machine learning models
%%capture
!pip install pytorch-lightning > /dev/null
!pip install gpytorch > /dev/null
import math
from typing import Sequence, Tuple
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch import Tensor
import gpytorch
from torch.utils.data import TensorDataset, DataLoader, random_split
import pytorch_lightning as pl
from pytorch_lightning import loggers as pl_loggers
7.2. Defining Symmetry Functions#
Now we will define the radial symmetry functions:
pairwise_vector: Distance function for calculating distances between each atom.
symmetry_function_g1: BP radial symmetry function.
symmetry_function_g2: BP angular symmetry function.
symmetry_function_g2ani: ANI angular symmetry function
def pairwise_vector(coords: Tensor) -> Tensor:
num_batches, num_channels, _ = coords.size()
rij = coords[:, :, None] - coords[:, None]
mask = ~torch.eye(num_channels, dtype=torch.bool, device=coords.device) # remove self-interaction
rij = torch.masked_select(rij, mask.unsqueeze(2)).view(num_batches, num_channels, num_channels - 1, 3)
return rij
def symmetry_function_g1(rij: Tensor, Rcr: float, EtaR: Tensor, ShfR: Tensor) -> Tensor:
dij = torch.norm(rij, dim=3)
fij = (torch.cos(dij / Rcr * math.pi) + 1) * 0.5 * (dij <= Rcr)
g1 = torch.sum(torch.exp(-EtaR.unsqueeze(dim=2) * (dij.unsqueeze(dim=-1) - ShfR.unsqueeze(dim=2))**2) * fij.unsqueeze(dim=-1), dim=2)
return g1
def symmetry_function_g2(rij: Tensor, Rca: float, Zeta: Tensor, EtaA: Tensor, LamA: Tensor) -> Tensor:
c = torch.combinations(torch.arange(rij.size(2)), r=2)
#print(c)
rij = rij[:, :, c]
r12 = rij[:, :, :, 0]
r13 = rij[:, :, :, 1]
r23 = r12 - r13
d12 = torch.norm(r12, dim=3)
d13 = torch.norm(r13, dim=3)
d23 = torch.norm(r23, dim=3)
f12 = (torch.cos(d12 / Rca * math.pi) + 1) * 0.5
f13 = (torch.cos(d13 / Rca * math.pi) + 1) * 0.5
f23 = (torch.cos(d23 / Rca * math.pi) + 1) * 0.5
cosine = torch.einsum('ijkl,ijkl->ijk', r12, r13) / (d12 * d13)
g2 = torch.sum(2**(1 - Zeta.unsqueeze(dim=2)) * (1 + LamA.unsqueeze(dim=2) * cosine.unsqueeze(dim=-1))**Zeta.unsqueeze(dim=2) * torch.exp(-EtaA.unsqueeze(dim=2) * (d12**2 + d13**2 + d23**2).unsqueeze(dim=-1)) * (f12 * f13 * f23).unsqueeze(dim=-1), dim=2)
return g2
def symmetry_function_g2ani(rij: Tensor, Rca: float, Zeta: Tensor, ShfZ: Tensor, EtaA: Tensor, ShfA: Tensor) -> Tensor:
c = torch.combinations(torch.arange(rij.size(2)), r=2)
rij = rij[:, :, c]
r12 = rij[:, :, :, 0]
r13 = rij[:, :, :, 1]
r23 = r12 - r13
d12 = torch.norm(r12, dim=3)
d13 = torch.norm(r13, dim=3)
f12 = (torch.cos(d12 / Rca * math.pi) + 1) * 0.5
f13 = (torch.cos(d13 / Rca * math.pi) + 1) * 0.5
cosine = torch.einsum('ijkl,ijkl->ijk', r12, r13) / (d12 * d13)
cosine = torch.cos(torch.acos(cosine).unsqueeze(dim=-1) - ShfA.unsqueeze(dim=2))
g2 = torch.sum(2**(1 - Zeta.unsqueeze(dim=2)) * (1 + cosine)**Zeta.unsqueeze(dim=2) * torch.exp(-EtaA.unsqueeze(dim=2) * (0.5 * (d12 + d13).unsqueeze(dim=-1) - ShfZ.unsqueeze(dim=2))**2) * (f12 * f13).unsqueeze(dim=-1), dim=2)
return g2
7.3. Defining Feature Extraction Classes#
7.3.1. Defining the BP Feature Class#
Now we will create the feature class, which takes input information and uses functions to extract characteristics unique to the called input features. Here we will be using the previously defined symmetry functions for feature extraction.
class Feature(nn.Module):
def __init__(self, Rcr: float, EtaR: Tensor, ShfR: Tensor, Rca: float, Zeta: Tensor, EtaA: Tensor, LamA: Tensor) -> None:
super().__init__()
assert len(EtaR) == len(ShfR) == len(LamA)
assert len(Zeta) == len(EtaA)
self.Rcr = Rcr
self.Rca = Rca
self.EtaR = torch.Tensor(EtaR)
self.ShfR = torch.Tensor(ShfR)
self.Zeta = torch.Tensor(Zeta)
self.EtaA = torch.Tensor(EtaA)
self.LamA = torch.Tensor(LamA)
def forward(self, coords: Tensor, atom_types: Tensor) -> Tensor:
num_batches, num_channels, _ = coords.size()
rij = pairwise_vector(coords)
EtaR = self.EtaR.to(device=coords.device)[atom_types]
ShfR = self.ShfR.to(device=coords.device)[atom_types]
Zeta = self.Zeta.to(device=coords.device)[atom_types]
EtaA = self.EtaA.to(device=coords.device)[atom_types]
LamA = self.LamA.to(device=coords.device)[atom_types]
g1 = symmetry_function_g1(rij, self.Rcr, EtaR, ShfR)
g2 = symmetry_function_g2(rij, self.Rca, Zeta, EtaA, LamA)
return torch.concat((g1, g2), dim=2)
@property
def output_length(self) -> int:
return len(self.EtaR[0]) + len(self.EtaA[0])
7.3.2. Defining the ANI Feature Class#
We will create a similar feature class for ANI that uses the ANI angle symmetry function.
class FeatureANI(nn.Module):
def __init__(self, Rcr: float, EtaR: Tensor, ShfR: Tensor, Rca: float, Zeta: Tensor, ShfZ: Tensor, EtaA: Tensor, ShfA: Tensor) -> None:
super().__init__()
assert len(EtaR) == len(ShfR)
assert len(Zeta) == len(ShfZ) == len(EtaA) == len(ShfA)
self.Rcr = Rcr
self.Rca = Rca
self.EtaR = torch.Tensor(EtaR)
self.ShfR = torch.Tensor(ShfR)
self.Zeta = torch.Tensor(Zeta)
self.ShfZ = torch.Tensor(ShfZ)
self.EtaA = torch.Tensor(EtaA)
self.ShfA = torch.Tensor(ShfA)
def forward(self, coords: Tensor, atom_types: Tensor) -> Tensor:
num_batches, num_channels, _ = coords.size()
rij = pairwise_vector(coords)
EtaR = self.EtaR.to(device=coords.device)[atom_types]
ShfR = self.ShfR.to(device=coords.device)[atom_types]
Zeta = self.Zeta.to(device=coords.device)[atom_types]
ShfZ = self.ShfZ.to(device=coords.device)[atom_types]
EtaA = self.EtaA.to(device=coords.device)[atom_types]
ShfA = self.ShfA.to(device=coords.device)[atom_types]
g1 = symmetry_function_g1(rij, self.Rcr, EtaR, ShfR)
g2 = symmetry_function_g2ani(rij, self.Rca, Zeta, ShfZ, EtaA, ShfA)
return torch.concat((g1, g2), dim=2)
@property
def output_length(self) -> int:
return len(self.EtaR[0]) + len(self.EtaA[0])
7.4. Creating the BP-GPR Model#
7.4.1. Defining the BP-GPR Class#
This class will combine the symmetry functions with the GPR model.
class BPGPR(gpytorch.models.ExactGP):
def __init__(self, descriptor: Tensor, Y: Tensor, likelihood, learning_rate=5e-4) -> None:
shape = descriptor.shape
X = descriptor #.reshape(shape[0], shape[1]*shape[2])
super(BPGPR, self).__init__(X, Y, likelihood)
self.mean_module = gpytorch.means.ConstantMean()
self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())
def forward(self, x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
7.4.2. Importing Data and Seeding#
We will now import our semiempirical and DFT calculation data.
import numpy as np
ds = np.DataSource(None)
qm_coord = np.array(np.load(ds.open("https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_coord.npy", "rb")), dtype="float32")
atom_types = np.loadtxt(ds.open("https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_elem.txt", "r"), dtype=int)
elems = np.unique(atom_types).tolist()
atom_types = np.array([[elems.index(i) for i in atom_types]])
atom_types = atom_types.repeat(len(qm_coord), axis=0)
energy = np.array((np.load(ds.open("https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy.npy", "rb")) - np.load(ds.open("https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy_sqm.npy", "rb"))) * 27.2114 * 23.061, dtype="float32")
energy = energy - energy.mean()
qm_gradient = np.array((np.load(ds.open("https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad.npy", "rb")) - np.load(ds.open("https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad_sqm.npy", "rb"))) * 27.2114 * 23.061 / 0.529177249, dtype="float32")
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
qm_coord = torch.from_numpy(qm_coord).to(device)
atom_types = torch.from_numpy(atom_types).to(device)
energy = torch.from_numpy(energy).to(device)
qm_gradient = torch.from_numpy(qm_gradient).to(device)
7.5. Using ANI for Feature Extraction#
The ANI model is set to be used and the ANI parameters are defined.
ani = True
if ani:
# From TorchANI
Rcr = 5.2000e+00
Rca = 3.5000e+00
EtaR = [1.6000000e+01]
ShfR = [9.0000000e-01,1.1687500e+00,1.4375000e+00,1.7062500e+00,1.9750000e+00,2.2437500e+00,2.5125000e+00,2.7812500e+00,3.0500000e+00,3.3187500e+00,3.5875000e+00,3.8562500e+00,4.1250000e+00,4.3937500e+00,4.6625000e+00,4.9312500e+00]
Zeta = [3.2000000e+01]
ShfZ = [1.9634954e-01,5.8904862e-01,9.8174770e-01,1.3744468e+00,1.7671459e+00,2.1598449e+00,2.5525440e+00,2.9452431e+00]
EtaA = [8.0000000e+00]
ShfA = [9.0000000e-01,1.5500000e+00,2.2000000e+00,2.8500000e+00]
EtaR, ShfR = np.array(np.meshgrid(EtaR, ShfR)).reshape(2, -1)
Zeta, ShfZ, EtaA, ShfA = np.array(np.meshgrid(Zeta, ShfZ, EtaA, ShfA)).reshape(4, -1)
EtaR = np.repeat([EtaR], 3, axis=0)
ShfR = np.repeat([ShfR], 3, axis=0)
Zeta = np.repeat([Zeta], 3, axis=0)
ShfZ = np.repeat([ShfZ], 3, axis=0)
EtaA = np.repeat([EtaA], 3, axis=0)
ShfA = np.repeat([ShfA], 3, axis=0)
descriptor = FeatureANI(Rcr, EtaR, ShfR, Rca, Zeta, ShfZ, EtaA, ShfA)
else:
Rcr = 6.0
Rca = 6.0
ShfR = np.zeros((3,6)) # H, C, O
EtaR = [0.0, 0.04, 0.14, 0.32, 0.71, 1.79]
EtaR = np.repeat([EtaR], 3, axis=0) # H, C, O
Zeta = [1, 2, 4, 8, 16, 32, 1, 2, 4, 8, 16, 32]
Zeta = np.repeat([Zeta], 3, axis=0) # H, C, O
EtaA = [0.0, 0.04, 0.14, 0.32, 0.71, 1.79, 0.0, 0.04, 0.14, 0.32, 0.71, 1.79]
EtaA = np.repeat([EtaA], 3, axis=0) # H, C, O
LamA = [1, 1, 1, 1, 1, 1, -1, -1, -1, -1, -1, -1]
LamA = np.repeat([LamA], 3, axis=0) # H, C, O
descriptor = Feature(Rcr, EtaR, ShfR, Rca, Zeta, EtaA, LamA)
7.6. GPR Hyperparameters#
7.6.1. Reshaping and Initializing#
The atom types and coordinates are reshaped with the energies for use in the regression kernel. Then the marginal likelihood function is initialized.
nskip = 1
# Reshape Matrix inputs to vector
X = descriptor.forward(qm_coord, atom_types)[::nskip,:,:]
shape = X.shape
X = X.reshape(shape[0], shape[1]*shape[2])
Y = energy[::nskip]
# Initialize likelihood and model
likelihood = gpytorch.likelihoods.GaussianLikelihood()
model = BPGPR(X, Y, likelihood)
7.6.2. Training the GPR Hyperparameters#
Now we can begin training to optimize the GPR hyperparameters.
training_iter = 500
# Find optimal model hyperparameters
model.train()
likelihood.train()
# Use the adam optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=0.1) # Includes GaussianLikelihood parameters
# "Loss" for GPs - the marginal log likelihood
mll = gpytorch.mlls.ExactMarginalLogLikelihood(likelihood, model)
for i in range(training_iter):
# Zero gradients from previous iteration
optimizer.zero_grad()
# Output from model
output = model(X)
# Calc loss and backprop gradients
loss = -mll(output, Y)
loss.backward()
if (i+1) % 100 == 0:
print('Iter %d/%d - Loss: %.3f outputscale: %.3f lengthscale: %.3f noise: %.3f' % (
i + 1, training_iter, loss.item(),
model.covar_module.outputscale.item(),
model.covar_module.base_kernel.lengthscale.item(),
model.likelihood.noise.item()
))
optimizer.step()
# Print Trained hyperparameters
print('outputscale: ', model.covar_module.outputscale.item())
print('lengthscale: ', model.covar_module.outputscale.item())
print('noise: ', model.likelihood.noise.item())
Iter 100/500 - Loss: 1.700 outputscale: 2.948 lengthscale: 3.301 noise: 0.851
Iter 200/500 - Loss: 1.516 outputscale: 4.564 lengthscale: 3.560 noise: 0.192
Iter 300/500 - Loss: 1.460 outputscale: 5.940 lengthscale: 3.748 noise: 0.074
Iter 400/500 - Loss: 1.400 outputscale: 7.171 lengthscale: 3.976 noise: 0.033
Iter 500/500 - Loss: 1.394 outputscale: 8.245 lengthscale: 4.165 noise: 0.018
outputscale: 8.256046295166016
lengthscale: 8.256046295166016
noise: 0.01762973517179489
7.7. Evaluating the Model’s Accuracy#
7.7.1. Evaluation of the Predicted Energy (RMSE)#
We will now calculate the RMSE for the energy and forces predicted by the BP-GPR mode
model.eval()
likelihood.eval()
# Prepare testing set
qm_coord = torch.autograd.Variable(qm_coord, requires_grad=True)
X_test = descriptor.forward(qm_coord, atom_types)
shape = X_test.shape
X_test = X_test.reshape(shape[0], shape[1]*shape[2])
# Make predictions
y_preds = likelihood(model(X_test))
y_mean = y_preds.mean
y_var = y_preds.variance
y_covar = y_preds.covariance_matrix
def eval(ref, pred):
rmse = torch.sqrt(torch.mean((ref-pred)**2))
q2 = 1 - torch.sum((ref-pred)**2)/torch.sum((ref-torch.mean(ref))**2)
return rmse, q2
print(torch.mean(y_var))
# Evaluate performance on energy predictions
y_rmse, y_q2 = eval(energy ,y_mean)
print("Energy Prediction RMSE: ", y_rmse.item(),"Q^2: ", y_q2.item())
/usr/local/lib/python3.10/dist-packages/gpytorch/models/exact_gp.py:284: GPInputWarning: The input matches the stored training data. Did you forget to call model.train()?
warnings.warn(
tensor(0.0675, grad_fn=<MeanBackward0>)
Energy Prediction RMSE: 0.050121136009693146 Q^2: 0.9998199343681335
7.7.2. Evaluation of the Predicted Forces (RMSE)#
auto_grad, = torch.autograd.grad(y_mean.sum(), [qm_coord])
rmse = torch.sqrt(torch.mean((auto_grad - qm_gradient)**2))
q2 = 1 - torch.sum((qm_gradient-auto_grad)**2)/torch.sum((qm_gradient-torch.mean(qm_gradient))**2)
print("Force RMSE: ", rmse.item(), "Q^2", q2.item())
Force RMSE: 4.071394920349121 Q^2 0.8092787265777588
7.7.3. Plotting RMSD for the BP-GPR Model#
Here we plot the RMSD for the predicted and reference energy and forces for the BP-GPR model.
import matplotlib.pyplot as plt
fig, ax = plt.subplots(1,2,figsize=(10,5))
e1 = energy.cpu().detach().numpy() + np.load(ds.open("https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy_sqm.npy","rb")) * 27.2114 * 23.061
e2 = y_mean.cpu().detach().numpy() + np.load(ds.open("https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/energy_sqm.npy","rb")) * 27.2114 * 23.061
ax[0].plot(e1, e2, linestyle='none', marker='.', color='springgreen')
ax[0].plot([np.max(np.concatenate((e1,e2))), -np.max(np.concatenate((e1,e2)))], [np.max(np.concatenate((e1,e2))), -np.max(np.concatenate((e1,e2)))], color="k", linewidth=1.5)
ax[0].set_xlabel("Reference Energy (kcal/mol)", size=14)
ax[0].set_ylabel("Predicted Energy (kcal/mol)", size=14)
ax[0].annotate('RMSD: %.3f' % np.sqrt(np.mean((e1 - e2)**2)), xy=(0.05, 0.95), xycoords='axes fraction', size=14)
f1 = -qm_gradient.cpu().detach().numpy().reshape(-1) - np.load(ds.open("https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad_sqm.npy","rb")).reshape(-1) * 27.2114 * 23.061 / 0.529177249
f2 = -auto_grad.cpu().detach().numpy().reshape(-1) - np.load(ds.open("https://github.com/cc-ats/mlp_tutorial/raw/main/Claisen_Rearrangement/qm_grad_sqm.npy","rb")).reshape(-1) * 27.2114 * 23.061 / 0.529177249
ax[1].plot(f1, f2, linestyle='none', marker='.', color='springgreen')
plt.plot([-np.abs(np.max(np.concatenate((f1,f2)))), np.max(np.concatenate((f1,f2)))], [-np.max(np.concatenate((f1,f2))), np.max(np.concatenate((f1,f2)))], color="k", linewidth=1.5)
ax[1].set_xlabel(r"Reference Force (kcal/mol/$\AA$)", size=14)
ax[1].set_ylabel(r"Predicted Force (kcal/mol/$\AA$)", size=14)
ax[1].annotate('RMSD: %.3f' % np.sqrt(np.mean((f1 - f2)**2)), xy=(0.05, 0.95), xycoords='axes fraction', size=14)
plt.tight_layout()
plt.savefig('rmsd.png', dpi=300)
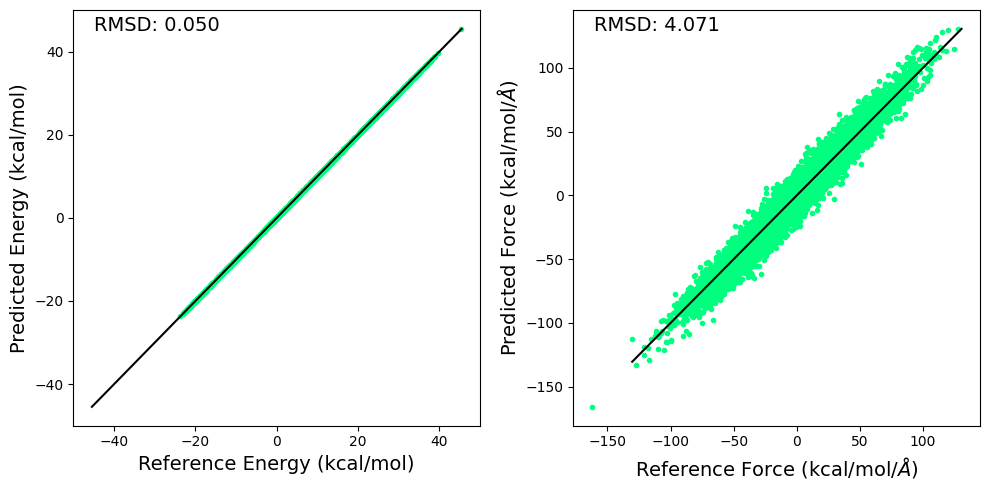
7.7.4. Tabulating the RMSE for the BP-GPR Model#
Finally, we can tabulate the RMSE for the BP-GPR model.
qm_coord_train = torch.autograd.Variable(qm_coord[::nskip,:,:], requires_grad=True)
X_train = descriptor.forward(qm_coord_train, atom_types[::nskip,:])
shape = X_train.shape
X_train = X_train.reshape(shape[0], shape[1]*shape[2])
# Make predictions
y_preds = likelihood(model(X_train))
y_mean = y_preds.mean
y_var = y_preds.variance
y_covar = y_preds.covariance_matrix
def eval(ref, pred):
rmse = torch.sqrt(torch.mean((ref-pred)**2))
q2 = 1 - torch.sum((ref-pred)**2)/torch.sum((ref-torch.mean(ref))**2)
return rmse, q2
# Evaluate performance on energy predictions
y_rmse, y_q2 = eval(Y ,y_mean)
print(f'Energy Prediction RMSE: {y_rmse.item():6>.4f}\t Q^2: {y_q2.item():6>.4f}')
# Evaluate Forces
auto_grad, = torch.autograd.grad(y_mean.sum(), [qm_coord_train])
rmse = torch.sqrt(torch.mean((auto_grad - qm_gradient[::nskip,:,:])**2))
q2 = 1 - torch.sum((qm_gradient[::nskip,:,:]-auto_grad)**2)/torch.sum((qm_gradient[::nskip,:,:]-torch.mean(qm_gradient[::nskip,:,:]))**2)
print(f'Force Prediction RMSE: {rmse.item():6>.4f}\t Q^2: {q2.item():6>.4f}')
Energy Prediction RMSE: 0.0501 Q^2: 0.9998
Force Prediction RMSE: 4.0714 Q^2: 0.8093
